43. Функция, непрерывная в точке , является ограниченной в некоторой окрестности этой точки.

Если функция непрерывна в точке и , то для всех Х, достаточно близких к .

Если функции и непрерывны в точке , то функции и тоже непрерывны в точке .

Если функции и непрерывны в точке , при этом , то функция тоже непрерывны в точке .

44. Функция, непрерывная на отрезке, равномерно непрерывна на нём.

Функция, непрерывная на отрезке, ограничена и достигает на нём свои максимальное и минимальное значения.

Областью значений функции , непрерывной на отрезке , является отрезок где минимум и максимум берутся по отрезку .

Если функция непрерывна на отрезке и то существует точка, в которой

Монотонная функция на отрезке непрерывна в том случае, когда область ее значений является отрезком с концами и .

45. Производной функции в точке называется предел отношения приращения функции в этой точке к приращению аргумента , при , то есть

Геометрический смысл производной: производная функции в точке касания равна угловому коэффициенту касательной проведенной к графику функции в этой точке. Производная равна k.

Дифференциала: Если к графику гладкой функции в некоторой точке построить касательную, то, отложив на касательной такой отрезок, чтобы его проекция на ось Ох равнялась ∆Х, получим в проекции на ось Оу отрезок, равный дифференциалу функции в точке касания.

46.

Т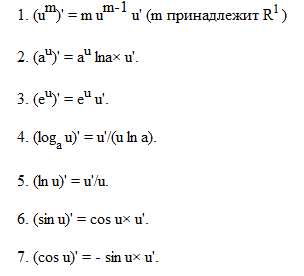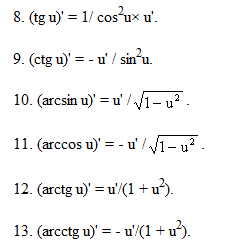аблица производных:

47. Если f '(x) — производная функции f (x), то производная от нее по независимой переменной x, (f '(x))' = f ''(x), называется производной второго порядка. Аналогично определены производные 3-го, 4-го, , и т.д, n-го порядка.

48. Дифференциал функции численно равен приращению касательной.

f(x) ≈ f(x₀) + f'(x₀)·Δx