
- •Вопросы по линейной алгебре и аналитической геометрии
- •Векторы и линейные операции над ними.
- •Базис. Координаты вектора.
- •Скалярное произведение векторов и его свойства.
- •Векторное произведение векторов и его свойства.
- •Смешанное произведение векторов и его свойства.
- •Общее уравнение прямой на плоскости, геометрический смысл его коэффициентов.
- •Уравнение прямой с угловым коэффициентом. Уравнение прямой в отрезках.
- •Расстояние от точки до прямой.
- •К аноническое уравнение эллипса (с выводом уравнения).
- •Канонические уравнения гипербола и параболы.
- •Уравнения прямой в пространстве.
- •Различные виды уравнений плоскости.
- •Эллипсоид, конус и гиперболоиды.
- •Параболоиды и цилиндрические поверхности.
- •Матрицы, виды матриц. Линейные операции над матрицами, их свойства. Умножение матриц, его свойства. Транспонирование матриц.
- •Определители матриц 1 и 2 порядков. Миноры и алгебраические дополнения элементов квадратных матриц. Вычисления определителя разложением по элементам строки или столбца.
- •Свойства определителей.
- •Обратная матрица, алгоритм ее нахождения.
- •Элементарные преобразования матриц.
- •Ранг матрицы.
- •Правило Крамера.
Вопросы по линейной алгебре и аналитической геометрии
Направленный отрезок и вектор. Длина отрезка, деление отрезка в данном отношении.
Векторы и линейные операции над ними.
Вектором наз. упорядоченная совокупность чисел Х={X1,X2,...Xn} вектор дан в n-мерном пространстве. Т(X1,X2,X3). n=1,2,3. Геометрический вектор - направленный отрезок. |AB|=|a| - длинна. 2 вектора наз. коллинеарными, если они лежат на 1 прямой или ||-ных прямых. Векторы наз. компланарными, если они лежат в 1-ой плоскости или в ||-ных плоскостях. 2 вектора равны, когда они коллинеарны, сонаправленны, и имеют одинак-ую длинну.
1.умножение на число: произведение вектора А на число l наз. такой вектор В, который обладает след. св-ми: а) А||В. б) l>0, то АВ, l<0, то А¯В. в)l>1, то А<В, )l<1, то А>В. 2. Разделить вектор на число n значит умножить его на число, обратное n: а/n=a*(1/n).
3.Суммой неск-их векторов а и в наз. соединяющий начало 1-го и конец последнего вектора. 4. Разностью векторов а и в наз-ся вектор c, который, будучи сложенным с вектором в даст вектор а.
Проекция вектора на ось.
Базис. Координаты вектора.
Б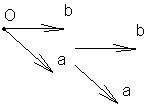 азисом
на плоскости называется совокупность
фиксированной точки и 2х неколлинеарных
векторов, проведенных к ней.
азисом
на плоскости называется совокупность
фиксированной точки и 2х неколлинеарных
векторов, проведенных к ней.
Б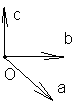 азисом
в пространстве наз. совокупность
фиксированной точки в пространстве и
3х некомпланарных векторов.
азисом
в пространстве наз. совокупность
фиксированной точки в пространстве и
3х некомпланарных векторов.
Любой вектор на плоскости может быть разложен по векторам базиса на плоскости. Любой вектор в пространстве может быть разложен по векторам базиса в пространстве.

ОС=OA+OB, OA=x*i, OB=j*y, OC=xi+yj. Числа х,у наз-ся координатами вектора ОС в данном базисе
Длиной вектора называется арифметическое значение квадратного корня и скалярного квадрата.
![]()
Длина вектора удовлетворяет следующим условиям:
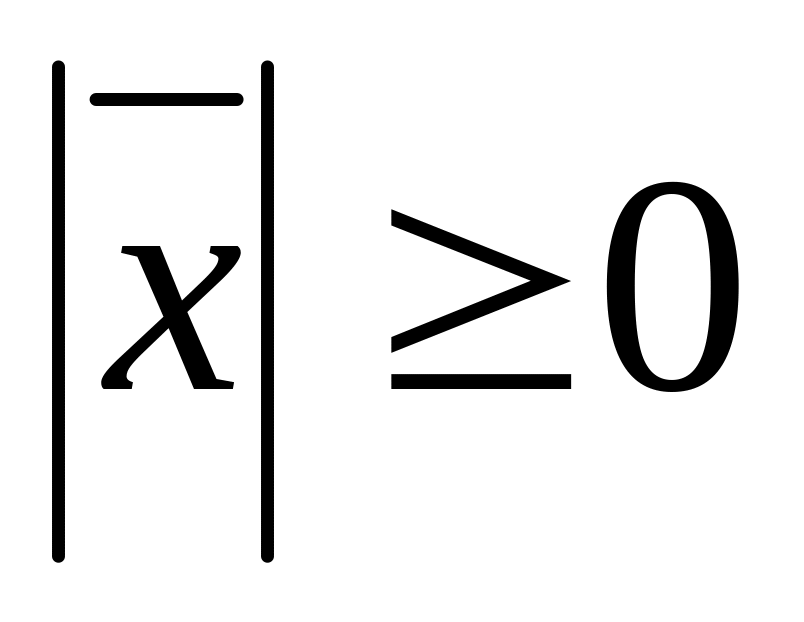 ,
если
,
если

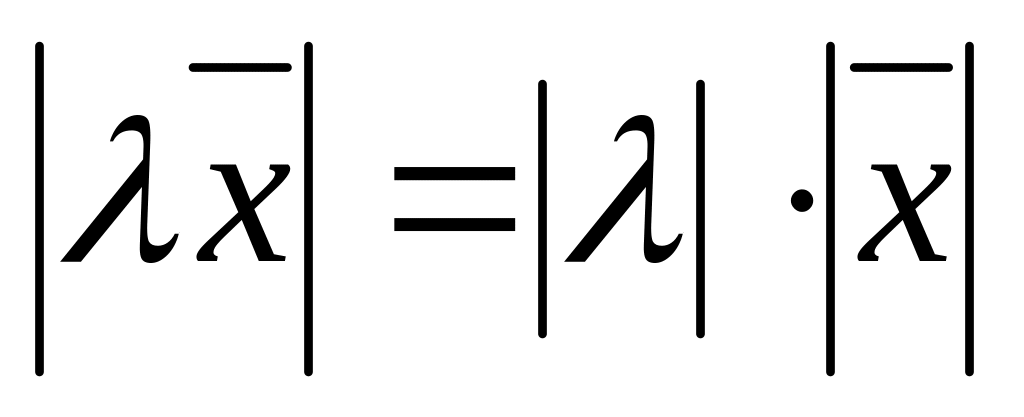
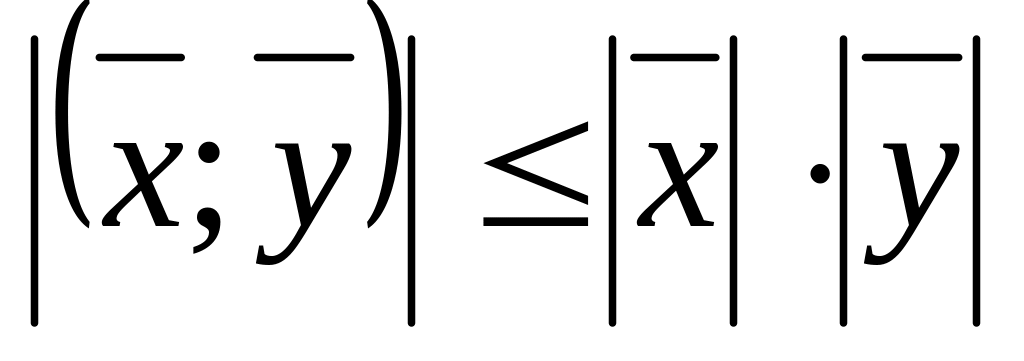 - неравенство
Коши-Буня
- неравенство
Коши-Буня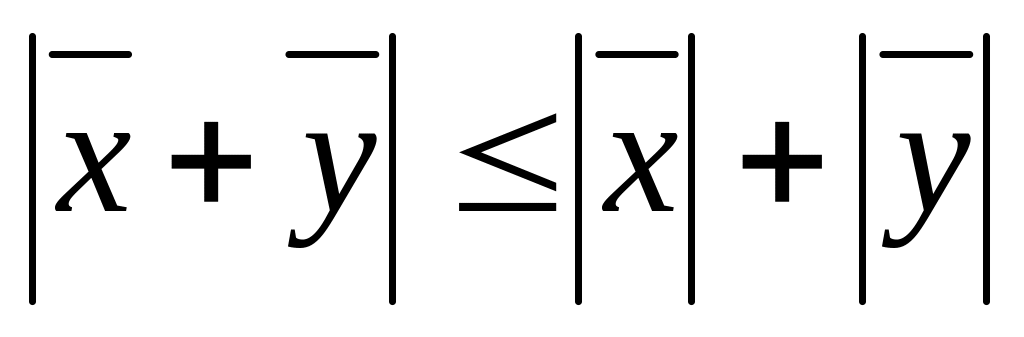 -
неравенство треугольника
-
неравенство треугольника
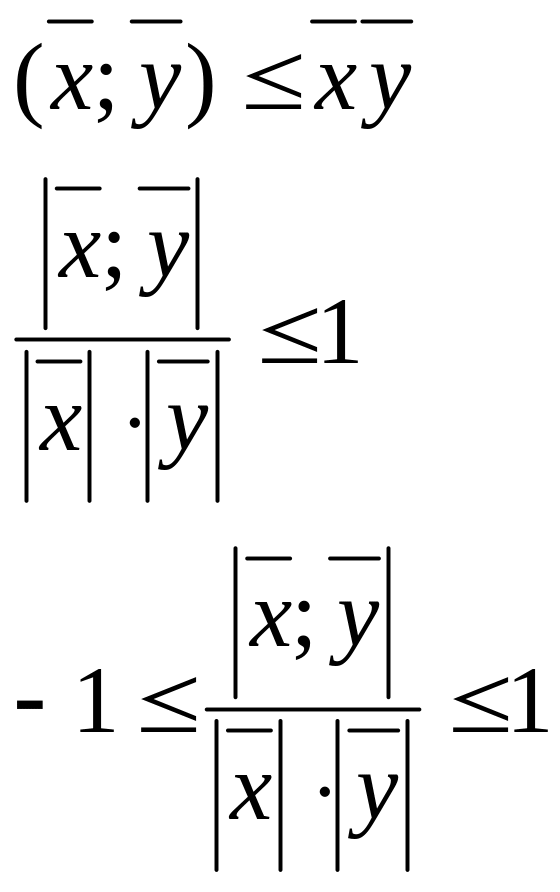
![]()
![]()
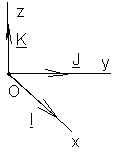
Аффинные координаты. Декартовы прямоугольные координаты.
Скалярное произведение векторов и его свойства.
Скалярным произведением двух ненулевых векторов называется число, равное произведению этих векторов на косинус угла между ними.
![]()
![]()
Cв-ва:
