
Вопрос №26 см. № 27
Вопрос № 27. Порядок цикла и порядок подстановки.
Любая подстановка φ конечного множества М может быть представлена в виде произведения взаимно простых циклических подстановок.
Такое представ. единственно с точностью до порядка следования сомножителей.
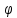 =
=
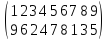
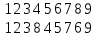
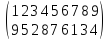
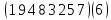
 =
=
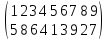
(1 5)(6 3)(2 8)(9 7)(4)
Порядком
подстановки называется минимальное
число
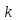 обладающего свойствами
обладающего свойствами
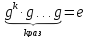
(3 2 4 5)(3 2 4 5)=(3 4)(2 5)=(3 5 4 2)·(3 2 4 5)
Порядок цикла равен количеству элементов, которое он перемещает.
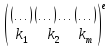 при
при

Порядок
этой подстановки – наименьшее общее
кратное порядков
 циклов
циклов
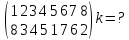
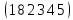
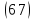
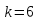
Вопрос № 28 Четность подстановки. Разложение подстановки в произведение транспозиций. Следствия. Т.Произведение двух подстановок одинаковой четности является четной подстановкой, а произведение двух подстановок разной четности – нечетной подстановкой.
Доказательство : Рассмотрим произведение двух подстановок :
AB=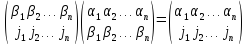
Если
подстановки одинаковой четности, то
они либо обе четны, либо обе нечетны. В
первом случае перестановки
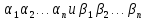 ,
а также
,
а также
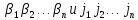 одинаковой
четности и значит перестановки
одинаковой
четности и значит перестановки
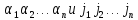 - тоже одинаковой четности. Во втором
случае перестановки
- тоже одинаковой четности. Во втором
случае перестановки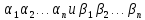 разной четности, но и подстановки
разной четности, но и подстановки
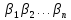 и
и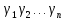 тоже разной четности, а значит перестановки
тоже разной четности, а значит перестановки
 одинаковой четности. И так в обоих
случаях подстановка AB четна.
одинаковой четности. И так в обоих
случаях подстановка AB четна.
Если
подстановки A и B разной четности, то
либо подстановка A четна, а B нечетна,
либо наоборот. Получим, что в обоих
случаях перестановки
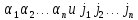 разной четности ⇒ AB нечетка.
Следствие: Все четные
подстановки симметрической группы
разной четности ⇒ AB нечетка.
Следствие: Все четные
подстановки симметрической группы
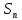 образуют
в ней подгруппу. Порядок равен
образуют
в ней подгруппу. Порядок равен
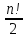 .
Это знакопеременная подгруппа (
.
Это знакопеременная подгруппа (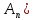 .
Любая
подстановка может быть представлена в
виде произв. транспозиций
.
Любая
подстановка может быть представлена в
виде произв. транспозиций
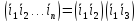 …
…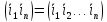
Пример (1 2 3 4 5 ) =( 1 2 ) ( 1 3 ) ( 1 4 ) ( 1 5 ) = ( 1 2 3 4 5 ) Сопряженные подстановки имеют одинаковую цикловую структуру.
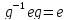
Доказательство:
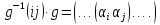 g=
g=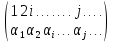
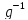 =
=
Произведение
циклов длины
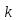
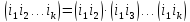
Умножив
левую часть на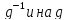
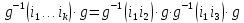 …
…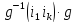

Пример:
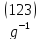
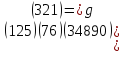
Вопрос № 29 Системы образующих симметрической группы.
Рассмотрим
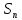

 n=3
T=
n=3
T=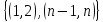
<
T > <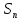
Элементы можно выписать в виде:

 =
0, 1, 2
=
0, 1, 2
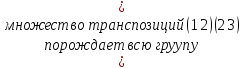
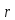 =1
=1
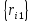 =
=
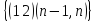
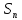 со
словами
элемент
со
словами
элемент
длиной
не более трех
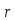 =2
=2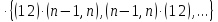
....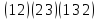
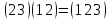
r=3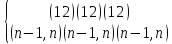
n=4
T=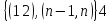
 =1
=1
 =2
=2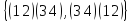
пока
разных
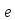 ,
,

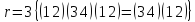
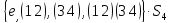
<
(1 2), (3 4)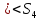
Величина
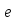
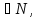 такая, что словами длины r
такая, что словами длины r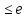 представимы
все элементы группы, которые порождаются
группой <T>, называется длиной
группы.
представимы
все элементы группы, которые порождаются
группой <T>, называется длиной
группы.
Вопрос № 30. Знакопеременная группа. Системы образующих этой группы.
Т.
Знакопеременная группа
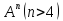 проста.
Лемма.
Если нормальная подстановка R гр.
проста.
Лемма.
Если нормальная подстановка R гр.
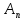 (
(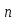 >2)
содержит цикл из трех элементов то R=
>2)
содержит цикл из трех элементов то R=
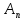 .
.
Доказательство. Пусть R содержит цикл ( 1 2 3 ), тогда R должен содержать и квадрат этого цикла ( 2 1 3 ) и все трансформированные из этого цикла элементы:
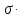 (
213)
(
213)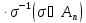
Возьмем
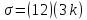 , где
, где
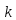 >3
>3
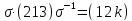 .
.
R содержит все циклы вида (1 2k).
Но
такие циклы порождают всю группу
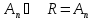 .
.
Доказательство
теоремы. Пусть R – произв. отлич. от
 норм. под-ка в
норм. под-ка в
 .
Надо доказать, что R=
.
Надо доказать, что R=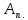 .
.
Выберем
в R подстановку
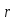 отличную от 1, и которая оставляет
неподвижными наибольшее возможное
количество чисел из тех, на которые
действуют подстановки из данной
симметрической группы. Покажем, что
отличную от 1, и которая оставляет
неподвижными наибольшее возможное
количество чисел из тех, на которые
действуют подстановки из данной
симметрической группы. Покажем, что
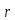 перестанавливает три числа, а остальные
не сдвигает с места.
перестанавливает три числа, а остальные
не сдвигает с места.
Предположим,
что
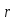 перестанавливает
4 элемента, тогда
перестанавливает
4 элемента, тогда
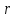 является произведением двух транспозиций.
Пусть
является произведением двух транспозиций.
Пусть
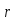 =(1
2)(3 4)
=(1
2)(3 4)
По
условию
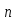 >4, поэтому
>4, поэтому
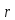 можно трансформировать с помощью
можно трансформировать с помощью
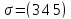 и получим:
и получим:
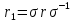 =(1 2)(45) .
=(1 2)(45) .
Произведение
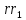 является тройным циклом (3 4 5) и
является тройным циклом (3 4 5) и
 переставляет меньше чисел, чем
переставляет меньше чисел, чем
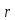 ,
что противоречит выбору
,
что противоречит выбору
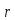 .
Таким образом, во всех случаях
.
Таким образом, во всех случаях
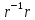 переставляет меньше чисел, чем
переставляет меньше чисел, чем
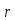 ,
что противоречит выбору
,
что противоречит выбору
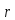 .
.
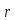 переставляет лишь 3 числа. Но тогда r-
тройной цикл и R=
переставляет лишь 3 числа. Но тогда r-
тройной цикл и R=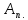 Доказано.
Доказано.
Вопрос 31 . Сопряженные элементы в симметрической группе.
См. вопрос 24.
Вопрос № 32. Уравнение Коши. Число его решений.
Это
уравнение вида
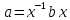
Пример:
( 1 2 3 4 ) ( 5 6 7 )·( 8 9 0 ) =
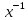 (
3 4 5 6 )( 7 8 0 )( 1 2 9 ) x.
(
3 4 5 6 )( 7 8 0 )( 1 2 9 ) x.
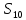 .
.
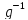 =
=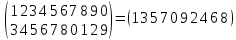 одно из решений.
одно из решений.
Остальные решения: Количество возможных замен местами циклов одинаковой длины.
Общее количество:
( кол-во элементов)·(замена местами циклов одинаковой длины)=
= 4·3·3·2= 72 решения.
Вопрос№33 Теорема Кэли
Теорема.
Для всякой группы G
существует изоморфная ей группа
подстановок (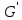 ,
M) на некотором подходящем множестве M.
,
M) на некотором подходящем множестве M.
Построим
одну такую группу подстановок. В качестве
M выберем множество G элементов группы
и сопоставим каждому
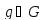 следующее отображение множества G:
следующее отображение множества G:
П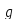 :
:
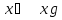
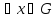
т.е.
мы сопоставляем групповому элементу
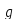 отображение множества G в себя, состоящее
в умножении всех элементов справа на
элемент
отображение множества G в себя, состоящее
в умножении всех элементов справа на
элемент
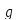 .
Такое отображение в гр. G называется
правым сдвигом. Отображение П
.
Такое отображение в гр. G называется
правым сдвигом. Отображение П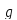 -
подстановка. Действительно,
-
подстановка. Действительно,
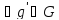 является образом при П
является образом при П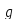 ,
а именно образом элемента
,
а именно образом элемента
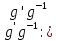 )·
)·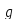 =
=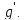 Отображение П
Отображение П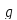 инъективно:
инъективно:
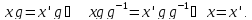
Пусть
G'
=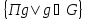 и покажем, что G' – группа подстановок.
Действительно, ведь П
и покажем, что G' – группа подстановок.
Действительно, ведь П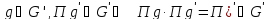 и П
и П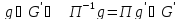 .
.
Пусть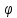 отображение
отображение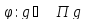
Группы
G на группу
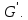 Отображение
Отображение - инъективно: если
- инъективно: если
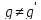 ,
то
,
то
П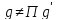 т.к. (1)·П
т.к. (1)·П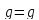 при П
при П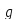 ,
а (1)·П
,
а (1)·П при П
при П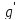 .
.
Имеем
(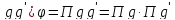 ,
т.к.
,
т.к.
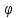 изоморфизм.
изоморфизм.
Построенная
группа (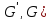 не единственная группа подстановок,
изоморфная данной группе. Построенная
группа наз. регулярным представителем
группы G.
не единственная группа подстановок,
изоморфная данной группе. Построенная
группа наз. регулярным представителем
группы G.
Вопрос №34
G=A+B=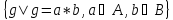
Вопрос 35. Прямое произведение подгруппы группы, свойства прямого произведения подгруппы.
Определение
1. Пусть даны группа
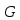 и две ее подгруппы
и две ее подгруппы
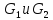 ,
причем выполнены следующие условия.
,
причем выполнены следующие условия.
-
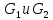 являются нормальными
делителями группы
являются нормальными
делителями группы
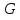 .
. -
пересечение
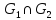 состоит только из единицы е.
состоит только из единицы е. -
каждый элемент группы G может быть представлен в виде произведения
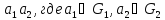 .
Тогда группа G называется прямым
произведением своих подгрупп
.
Тогда группа G называется прямым
произведением своих подгрупп
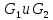 ;
;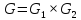 .
.
Т. Каждый
элемент группы
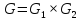 однозначно представляется в виде
произведения
однозначно представляется в виде
произведения
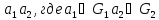 .
.
Каждый
элемент
 ,
коммутирует с каждым элементом
,
коммутирует с каждым элементом
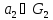 ( т.е.
( т.е.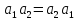 ).
).
Доказательство.
Предположим, что какой-то элемент группы
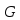 двумя способами представлен в вмде
произведения элементов подгрупп
двумя способами представлен в вмде
произведения элементов подгрупп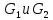
 .
.
Умножая
обе части последнего равенства слева
на
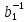 ,
а справа на
,
а справа на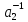 получим
получим
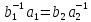
Но
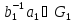 ,
,
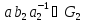 и значит, элемент принадлежит пересечению
и значит, элемент принадлежит пересечению
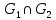 т.е. равен
т.е. равен
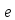 :
:
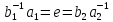
откуда
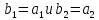 .
.
ΙΙ.
Пусть
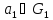 и
и
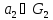 .
Рассмотрим так называемый коммутатор
этих элементов
.
Рассмотрим так называемый коммутатор
этих элементов
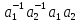
Произведение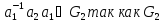 - нормальный делитель и значит
- нормальный делитель и значит
произведение
(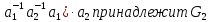 .
.
С другой
стороны произведение
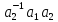 принадлежит
принадлежит
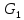 т.к.
т.к.
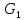 -
нормальный делитель и значит
-
нормальный делитель и значит
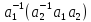 принадлежит
принадлежит
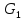 .
Таким образом, коммутатор принадлежит
пересечению
.
Таким образом, коммутатор принадлежит
пересечению
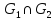 .
и поэтому он равен
.
и поэтому он равен
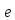 .
.
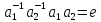
Умножая
последнее равенство слева на
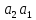 ,
получим:
,
получим:
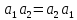 т.е. любой элемент из
т.е. любой элемент из
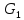 коммутирует с любым элементом из
коммутирует с любым элементом из
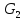 .
.
Аналогично
можно определить прямое произведение
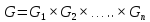
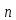 множителей. Здесь все подгруппы
множителей. Здесь все подгруппы являются нормальными делителями G,
пересечение каждой из подгрупп
являются нормальными делителями G,
пересечение каждой из подгрупп
 с подгруппой, порожденной в G всеми
остальными множителями
с подгруппой, порожденной в G всеми
остальными множителями
 состоит только из единицы и каждый
элемент группы G можно представить в
виде произведения
состоит только из единицы и каждый
элемент группы G можно представить в
виде произведения
 где
где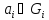 .
.
Теперь видно, что порядок прямого произведения конечных групп равен произведению порядков сомножителей.
Пример:
Прямое произведение циклической групп
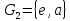 второго порядка и циклич. группы
второго порядка и циклич. группы
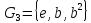 третьего порядка кроме элементов ,
третьего порядка кроме элементов ,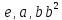 должно содержать произведения
должно содержать произведения
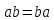 и
и
 .
.
Видно,
что эта группа является циклической
группой
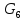 .
.
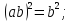
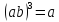
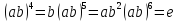
Итак
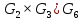 .
.
Вопрос 36. Нормальные делители группы, их свойства.
Определение.
Подгруппа A называется норм. делителем
группы G, если
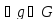
будет
выполнено
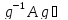 A.
A.
Т. Пересечение двух норм. делителей группы G само является нормальным делителем G.
Доказательство.
Пусть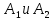 нормальные делители группы G и A=
нормальные делители группы G и A=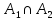 .
.
А подгруппа
в G. Далее т.к. A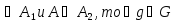 будет выполднено
будет выполднено
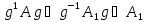
и
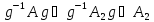
т.е. A – нормальный делитель группы G.
Т. Для того
чтобы подгруппа A группы G была норм.
делителем G, необходимо и достаточно ,
чтобы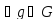 имело место равенство
имело место равенство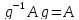 .
.
Доказательство.
Достаточность этого условия следует
из определения. Для того, чтобы доказать
необходимость предположим A – нормальный
делитель группы G, тогда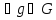 .
.
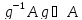 .
а значит и
.
а значит и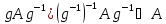 откуда и следует, что A
откуда и следует, что A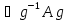
Но если
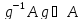 и A
и A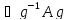 ,
то
,
то
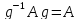 .
Доказано.
.
Доказано.
Т. Для того чтобы подгруппа A была норм. делителем группы G необходимо и достаточно, чтобы левые и правые смежные классы группы G по подгруппе A совпадали.
Доказательство.
Из равенства
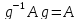 вытекает, что A
вытекает, что A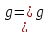 A.
A.
т.е., что
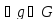 левый и правый смежный классы,
содержащие этот элемент, совпадают.
Обратно если
левый и правый смежный классы,
содержащие этот элемент, совпадают.
Обратно если
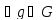 будет
будет
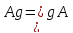 то
то
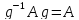

 норм. делитель.
норм. делитель.
Вопрос № 37 Понятие гомоморфизма групп. Ядро гомоморфизма групп.
Пусть
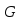 группа и
группа и
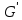 (
(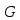 ,
∗) (
,
∗) (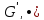
-
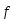 :
G
:
G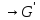 - изоморфизм,
если выполнены :
а)
- изоморфизм,
если выполнены :
а)
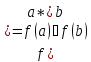 б) |G|=|
б) |G|=| группы равномощны, если для элементов
этих групп построить биективное
отображение.
Гомоморфизмом называется такое
отображение f группы G в группу
группы равномощны, если для элементов
этих групп построить биективное
отображение.
Гомоморфизмом называется такое
отображение f группы G в группу
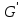 если выполнено хотя бы одно из условий
а) или б). Таким образом, изоморфизм
частный случай гомоморфизма.
если выполнено хотя бы одно из условий
а) или б). Таким образом, изоморфизм
частный случай гомоморфизма.
Определение.
Множество элементов группы G, которые
при любом гомоморфизме
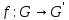 отображаются в единичный элемент группы
отображаются в единичный элемент группы
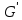 , называется ядром группы.
Ядро любого
гомоморфизма группы G является ее
нормальным делителем.
, называется ядром группы.
Ядро любого
гомоморфизма группы G является ее
нормальным делителем.
H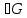

G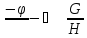 H
H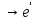 H-ядро гомоморфизма.
H-ядро гомоморфизма.
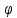 (G)=
(G)=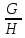 Пусть G
Пусть G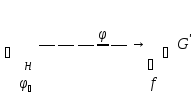 H⊲G
H⊲G
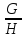
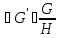 такой
что
такой
что
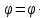 f
f
Доказательство.
Пусть
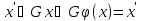
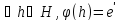
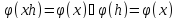
{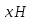 }
}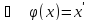
Пусть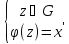
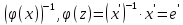
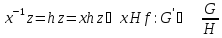
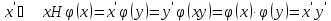
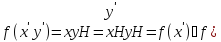 )
)

Вопрос №38 теорема в вопросе 37.
Вопрос №39.Кольца, коммутативные кольца и кольца с единицей. Примеры. Основные тождества в кольце.
Кольцо
- непустое множество, на котором заданы
бинарные операции, (K,+, )
которые удовлетворяют следующим
аксиомам:
)
которые удовлетворяют следующим
аксиомам:
-
(
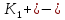 абелева группа
абелева группа -
(
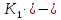 полугруппа
полугруппа -
(
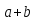 )
) c=
c=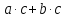 c
c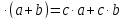
Дистрибутивность
Если в аксиоме 2) будет полугруппа с единицей, то соответственно кольцо называется кольцо с единицей.
А если еще полугруппа коммутативна, то кольцо называется коммутативным.
(Z,+, кольца:
кольца:
(Q,+,
(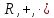
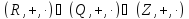 .
.
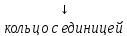
 -
кольцо с единицей
-
кольцо с единицей
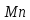 (R)
(R)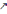
Доказательство:1) замкнутость относительно операции +
нейтральный
элемент по сложению
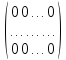
нейтральный
элемент по умножению E=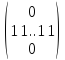
Основные тождества
1)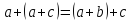 2)
2)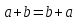
3)разрешимо
уравнение
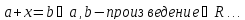
4)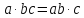
5)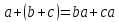
6)
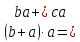
7)
если
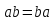 -
коммутативны по умножению
Целые числа
образуют кольцо с единицей.
-
коммутативны по умножению
Целые числа
образуют кольцо с единицей.
Вопрос №40 . Делители нуля и обратимые элементы в кольце. Идеалы кольца.
Делители
нуля. В произв. кольце R для некоторых
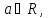
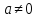 уравнение
уравнение
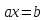 может
иметь для некоторых b больше, чем одно
решение, скажем
может
иметь для некоторых b больше, чем одно
решение, скажем
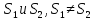 .
Тогда
.
Тогда
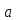 (
(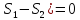 причем
причем
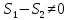 обратно если для a
обратно если для a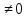 существует элемент S
существует элемент S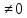 для
которого
для
которого
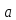 S=0
то уже уравнение :
S=0
то уже уравнение :
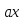 =0
имеет как минимум два решения: 0 и S.
=0
имеет как минимум два решения: 0 и S.
Элемент
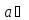 R,
R,
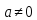 называется делителем нуля, если существует
элемент
называется делителем нуля, если существует
элемент
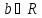 ,
,
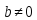 ,
такой что
,
такой что
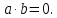
Если R-поле, то делитель нуля оно не содержит.
Но в кольцах R не являясь полями, могут быть элементы, делящие все элементы кольца. В кольце целых чисел это - -1, и 1.
Элемент
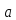 кольца R называется обратным, если он
делит все элементы из R.
кольца R называется обратным, если он
делит все элементы из R.
Множество всех обратимых элементов кольца с единицей образуют группу ( мультипликативную ).
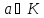 f
f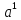

Непустое подмножество J кольца R называется идеалом этого кольца, если оно замкнуто относительно сложения и вычитания и относительно умножения на произв. элемент из R:
J
идеал R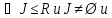
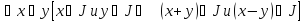 и
и
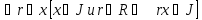
-
Все кольцо R является идеалом самого себя и называется единичным идеалом.
-
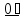 содержится
в любом идеале
содержится
в любом идеале -
Под-во
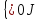 - наз. нулевой идеал.
- наз. нулевой идеал. -
Если идеал J содержит 1
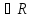 ,
то он содержит все элементы кольца и
совп. с единичным идеалом. J = е
,
то он содержит все элементы кольца и
совп. с единичным идеалом. J = е
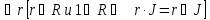 .
.
Вопрос № 41. Идеалы в кольце целых чисел. Сравнения целых чисел по модулю, их свойства. Идеал содержит - -1 и +1. Легко доказать по определению идеала.
Сравнения. Два числа сравнимые с третьим сравнимы между собой.
Сравнения
можно складывать почленно
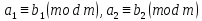
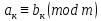
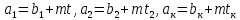 откуда
откуда
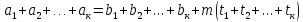
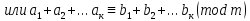 .
.
Слагаемое можно перенести в другую сторону с обратным знаком.
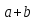 ≡
≡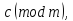 -b
≡-b
-b
≡-b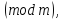
 ≡c-b
≡c-b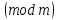 .
.
Сравнения можно перемножать.
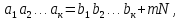 N
–
целое
N
–
целое
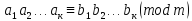
Обе части сравн. можно умножить на одно и то же число и возвести в одну и ту же степень.
Действ.
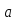 ≡
≡
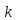 ≡
≡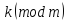 то
то
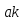 ≡
≡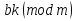
Обе части сравнения можно разделить на их общий делитель, если он взаимно прост с модулем.
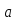 ≡
≡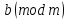
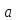 =
=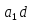 .
.
 =
=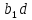 .
.
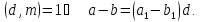
делится
на
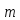 поэтому
поэтому
 делится на
делится на
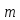 т.е.
т.е.

Обе части сравнения и модуль можно умножить на одно и то же целое.
Из
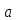 ≡
≡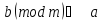 =
=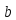 +
+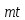 ,
,
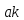 =
=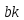 +
+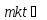
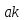 ≡
≡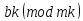 .
.
Обе части сравнения и модуль можно разделить на любой их общий делитель.
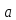 ≡
≡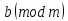
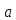 =
=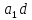 b=
b=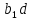 m=
m=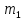 d.
d.
Имеем
 +
+
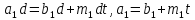
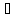
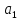 ≡
≡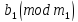 .
.
Вопрос № 42. Построение кольца класса вычетов . Его свойства.
Утв. Каждому гомоморфизму соответствует некоторый двусторонний идеал, являющийся его ядром.
Вопрос
. Существует ли гомоморфный образ
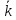 кольца
кольца
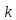 ,
такой что классы вычетов по идеалу m
отображаются в элементы кольца
,
такой что классы вычетов по идеалу m
отображаются в элементы кольца
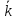 ?
?
Чтобы
построить такое кольцо в качестве
элементов конструируемого кольца,
возьмём просто классы вычетов по модулю
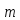 :
класс вычетов
:
класс вычетов
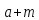 обозначим через
обозначим через
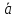 ,
класс вычетов
,
класс вычетов
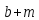 - через
- через
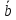 и определим
и определим
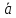 +
+
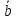 -- как класс, в котором лежит сумма
-- как класс, в котором лежит сумма
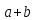 ,
и
,
и
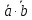 - как класс, в котором лежит произведение
- как класс, в котором лежит произведение
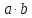 .
Если
.
Если
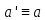 - какой -нибудь другой элемент из
- какой -нибудь другой элемент из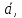 ab'≡b другой элемент из
ab'≡b другой элемент из
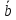 ,
то
,
то
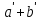 ≡
≡
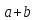
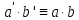
Следовательно
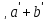 лежит в том же классе вычетов, что и
лежит в том же классе вычетов, что и
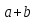 ,
так же
,
так же
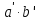 лежит в том же классе вычетов, что и
лежит в том же классе вычетов, что и
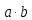 .
Таким образом наше определение суммы
и произведения классов не зависит от
выбора элементов
.
Таким образом наше определение суммы
и произведения классов не зависит от
выбора элементов
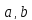 в классах
в классах
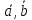 .
.
Каждому
элементу
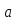 соответствует класс вычетов
соответствует класс вычетов
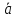 , и это отображение гомоморфно, потому
что сумма
, и это отображение гомоморфно, потому
что сумма
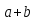 переходит
в сумму
переходит
в сумму
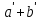 ,
а произведение
,
а произведение
 переходит в
переходит в
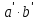 .
Следовательно классы вычетов образуют
кольцо, так называемое кольцо классов
вычетов или фактор кольцом кольца K по
идеалу
.
Следовательно классы вычетов образуют
кольцо, так называемое кольцо классов
вычетов или фактор кольцом кольца K по
идеалу
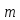 .
При этом соответствии кольцо K гомоморфно
отображается на кольце
.
При этом соответствии кольцо K гомоморфно
отображается на кольце
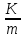 .
.
Двусторонние идеалы позволяют строить кольца гомоморфные данному кольцу. Элементами такого нового кольца являются классы вычетов по некоторому двустороннему идеалу. Любые два класса вычетов складываются и умножаются, потому что можно складывать и умножать два произвольных представителя этих классов.
Из
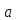 ≡
≡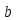 следует, что
следует, что
 теперь сравнения при переходе к классам
вычетов становятся равенствами, и
операции над сравнениями в кольце K
соответствуют операциям над равенствами
в кольце
теперь сравнения при переходе к классам
вычетов становятся равенствами, и
операции над сравнениями в кольце K
соответствуют операциям над равенствами
в кольце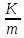 .
.
Теорема.
Каждое кольцо, гомоморфное кольцу
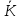 изоморфно по неко-торому кольцу классов
вычетов
изоморфно по неко-торому кольцу классов
вычетов
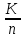 .
При этом n-двусторонний
идеал, элементы которого имеют нулевой
образ в
.
При этом n-двусторонний
идеал, элементы которого имеют нулевой
образ в
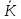 .
Обратно. Любое кольцо классов вычетов
.
Обратно. Любое кольцо классов вычетов
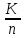 является
гомоморфным образом кольца K.
является
гомоморфным образом кольца K.
Примеры.
В кольце целых чисел классы вычетов по
произвольному полож. m>0
обозначим
 ,
где
,
где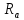 состоит из чисел, которые при делении
на m дают остаток
состоит из чисел, которые при делении
на m дают остаток
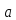 .
Чтобы сложить или перемножить два
класса вычетов
.
Чтобы сложить или перемножить два
класса вычетов
 ,
нужно сложить или соответственно
перемножить их представителей
,
нужно сложить или соответственно
перемножить их представителей
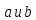 и привести результат к его наименьшему
неотрицательному остатку от деления
на m.
и привести результат к его наименьшему
неотрицательному остатку от деления
на m.
Вопрос № 43.
Вопрос № 44. Сравнения первой степени с одним неизвестным.
Сравнения первой степени перенесением свободного члена ( с обратным знаком) в правую часть можно привести к виду
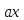 ≡
≡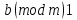
Ограничим
пока сравнение условием (
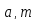 )=1.
Это сравнение имеет столько решений,
сколько вычетов полной системы ему
удовлетворяет. Но когда
)=1.
Это сравнение имеет столько решений,
сколько вычетов полной системы ему
удовлетворяет. Но когда
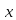 пробегает полную систему вычетов по
модулю
пробегает полную систему вычетов по
модулю
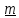 ,
то
,
то
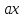 пробегает
полную систему вычетов. Следовательно,
при одном и только одном значении
пробегает
полную систему вычетов. Следовательно,
при одном и только одном значении
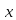 , взятом из полной системы,
, взятом из полной системы,
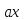 будет сравнимо с
будет сравнимо с
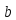 .
Итак, при (
.
Итак, при (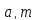 )=1
сравнение
)=1
сравнение
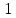 имеет одно решение.
имеет одно решение.
Пусть
теперь (
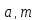 )=
)=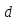 >1.
Тогда, чтобы сравнение
>1.
Тогда, чтобы сравнение
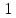 имело решения, необходимо чтобы
имело решения, необходимо чтобы
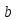 делилось на
делилось на
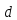 ,
иначе сравнение
,
иначе сравнение
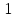 невозможно ни при каком целом
невозможно ни при каком целом
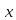 .
Предполагая поэтому
.
Предполагая поэтому
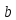 кратным
кратным
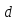 положим
положим
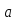 =
=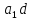 ,
,
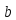 =
=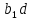 ,
,
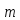 =
=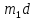 .
Тогда сравнение
.
Тогда сравнение
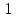 будет равносильно такому ( по сокр. на
d):
будет равносильно такому ( по сокр. на
d):
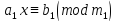 ,
в котором уже (
,
в котором уже (
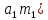 =
1 и потому оно будет иметь одно решение
по модулю
=
1 и потому оно будет иметь одно решение
по модулю
 .
Пусть
.
Пусть
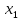 - наименьший неотрицательный вычет
этого решения по модулю
- наименьший неотрицательный вычет
этого решения по модулю
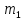 ,
тогда все числа
,
тогда все числа
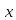 ,
образующие это решение, найдутся в виде
,
образующие это решение, найдутся в виде
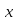 ≡
≡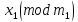 -
-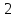
По
модулю же
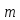 числа из
числа из
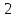 образуют не одно решение, а больше,
столько, сколько чисел из
образуют не одно решение, а больше,
столько, сколько чисел из
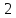 найдется в ряде: 0, 1, 2,….,m-1 наименьших
неотрицательных вычетов по модулю
найдется в ряде: 0, 1, 2,….,m-1 наименьших
неотрицательных вычетов по модулю
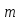 .
Сюда попадут следующие числа из
.
Сюда попадут следующие числа из
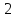
 ,
т.е всего
,
т.е всего
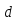 чисел
из
чисел
из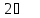 сравнение
сравнение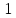 имеет
имеет
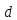 решений.
решений.
Т.
Пусть (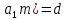 .
Сравнение
.
Сравнение
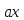 =
= (mod
m) невозможно, если
(mod
m) невозможно, если
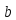 не делится на
не делится на
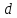 .
При
.
При
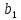 кратном
кратном
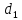 сравнение имеет
сравнение имеет
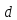 решений. Разыскивая решения сравнения
решений. Разыскивая решения сравнения
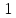 и ( способ, основанный на теории непрерывных
дробей, ограничимся случаем (
и ( способ, основанный на теории непрерывных
дробей, ограничимся случаем (
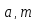 )=1.
)=1.
Разлагая
в непрерывную дробь отношение m: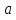
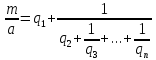
И рассматривая две последние подходящие дроби:
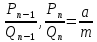 .
.
Согласно
свойствам непр. дробей
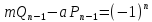 ,
,
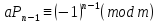
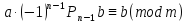
Итак
сравнение имеет вид
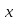 ≡
≡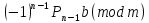
Для
разыскания которого достаточно вычислить
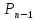 ,
,
Пример Решим сравнение:
111x≡75(mod321)
Здесь ( 1 1 1, 3 2 1)=3, причем 75 кратно 3, поэтому сравнение имеет три решения.
Деля обе части сравнения и модуль на 3, получим сравнение
37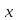 ≡25(
mod107),которое ещё надо сначала решить
≡25(
mod107),которое ещё надо сначала решить
q 2 1 8 4
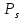 1 2 3 2 6 107
107 |
1 2 3 2 6 107
107 |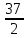
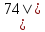
37|33
33|
33|4
32|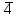
|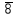
4
|

4
|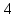
В
данном случае n=4.
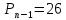
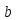 =25
=25
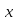 ≡-26
≡-26 25≡99(mod107)
Решения
25≡99(mod107)
Решения
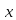 ≡99+107;
99+
≡99+107;
99+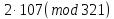
т.е.
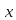 ≡99,206,313
≡99,206,313
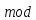 (321).
(321).
