21) Определение угла между прямой и плоскостью.
Углом между прямой и плоскостью называется любой угол между прямой и ее проекцией на эту плоскость.
22) Определение угла между скрещивающимися прямыми.
Углом между скрещивающимися прямыми
называется угол между пересекающимися
прямыми, соответственно параллельными
данным. Это означает, что через произвольную
точку 
пространства
проводятся прямые 
и 
,
соответственно параллельные прямым 
и 
,
и угол между 
и 
по
определению равен углу между пересекающимися
прямыми 
и 
.
При таком определении случай,
когда точка 
лежит
на одной из данных прямых (например, на
прямой 
),
приходится рассматривать отдельно, так
как в большинстве учебников прямая не
считается параллельной самой себе.
Тогда через точку 
проводится прямая 
,
параллельная прямой 
.
В этом случае угол между
прямыми 
и 
---
это угол между пересекающимися
прямыми 
и 
.
Поскольку точка 
выбирается
произвольным образом, необходимо
доказать, что угол между
скрещивающимися прямыми один и тот же
при любом выборе этой точки.
23) Аксонометрические проекции. Их образование, прямоугольная и косоугольные аксонометрии.
Аксонометрическая проекция — способ изображения геометрических предметов на чертеже при помощи параллельных проекций.
Предмет с системой координат, к которой он отнесён, проецируют на произвольную плоскость (картинная плоскость аксонометрической проекции) таким образом, чтобы эта плоскость не совпадала с его координатной плоскостью. В этом случае получается две взаимосвязанные проекции одной фигуры на одну плоскость, что позволяет восстановить положение в пространстве, получив наглядное изображение предмета. Так как картинная плоскость не параллельна ни одной из координатных осей, то имеются искажения отрезков по длине параллельных координатным осям. Это искажение может быть равным по всем трём осям — изометрическая проекция, одинаковыми по двум осям — диметрическая проекция и с искажениями разными по всем трём осям — триметрическая проекция.
Аксонометрическая проекция
-
прямоугольная проекция (направление проецирования перпендикулярно к плоскости проекции):
-
прямоугольная изометрическая проекция;
-
прямоугольная диметрическая проекция;
-
-
косоугольная проекция (направление проецирования не перпендикулярно к плоскости проекции):
-
фронтальная изометрическая проекция;
-
фронтальная диметрическая проекция;
-
горизонтальная изометрическая проекция.
-
24) Каковы коэффициенты искажения по направлениям осей в прямоугольной изометрии и диметрии, углы между осями прямоугольной изометрии и диметрии.
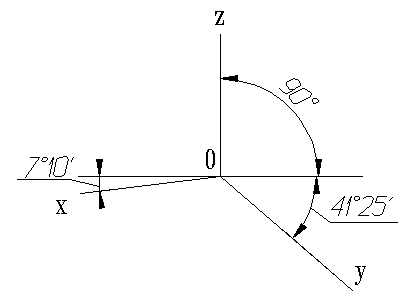
Изометрическая проекция
Коэффициент искажения по осям x, y, z равен 0.82.
Изометрическую проекцию для упрощения, как правило выполняют без искажения по осям x, y, z, т.е. приняв коэффициент искажения равным 1.
Окружности, лежащие в плоскостях, параллельных плоскостям проекций, проецируются на аксонометрическую плоскость проекций в эллипсы/
Если аксонометрическую проекцию выполняют без искажения по осям x, y, z, то большая ось эллипсов 1,2, 3 равна 1,22, а малая ось - 0.71 диаметра окружности.
Если аксонометрическую проекцию выполняют с искажением по осям x, y, z, то большая ось ось эллипсов 1, 2, 3 равна диаметру окружности, а малая - 0.58 диаметра окружности.
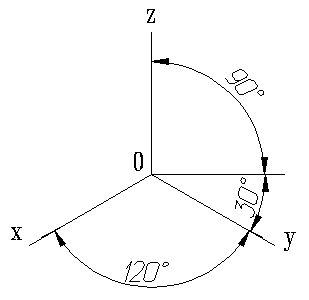
Диметрическая проекция
Коэффициент искажения по оси y равен 0.47, а по осям x и z - 0.94.
Диметрическую проекцию, как правило, без искажения по осям x и z и с коэффициентом искажения 0.5 по оси y.
Окружности, лежащие в плоскостях, параллельных плоскостям проекций, проецируются на аксонометрическую плоскость проекций в эллипсы.
Если димметрическую проекцию выполняют без искажения по осям x и z то большая ось эллипсов 1, 2, 3 равна 1,06 диаметра окружности, а малая ось эллипса 1 - 0.95, эллипсов 2 и 3 - 0.35 диаметра окружности.
Если диметрическую проекцию выполняют с искажения по осям x и z, то большая ось эллипсов 1, 2, 3 равна диаметру окружности, а малая ось эллипса 1 - 0.9, эллипсов 2 и 3 - 0,33 диаметра окружности.
