Документ Microsoft Office Word (4)

Среднее арифметическое является наиболее общим и самым распространённым понятием средней величины. Термин "среднее арифметическое" предпочитают в математике и статистике, чтобы отличать его от других средних величин, таких как медиана и мода. Частными случаями среднего арифметического являются генеральное среднее (генеральной совокупности) и выборочное среднее (выборки). 7. Свойство 1. Среднее арифметическое постоянной величины равно этой постоянной. Пусть при исследовании признака x он n раз принимал одно и то же значение c. Тогда Свойство 2. Если каждое значение признака Z равно сумме (разности) значений признаков X и Y, то среднее арифметическое признака Z равно сумме (разности) средних арифметических признаков X и Y. 9. Средняя гармоническая — используется в тех случаях когда известны индивидуальные значения признака и произведение , а частоты неизвестны. В примере ниже — урожайность известна, — площадь неизвестна (хотя её можно вычислить делением валового сбора зерновых на урожайность), — валовый сбор зерна известен. Среднегармоническую величину можно определить по следующей формуле: Формула средней гармонической:

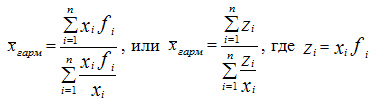
Семинарское занятие№6 ( 2 часа)

Тема: Расчёт и применение показателей вариации в статистическом исследовании

1. Задачи статистического изучения вариации.

2. Математические свойства дисперсии.

3. Расчет дисперсии на основе ее математических свойств.

4. Дисперсия альтернативного признака.

5. Меры вариации для сгруппированных данных: общая дисперсия, групповая, межгрупповая.

6. Правило сложения дисперсий.

7. Эмпирическое корреляционное отношение.

1. Вариация – это различия в значениях того или иного признака у отдельных единиц, входящих в данную совокупность. Она возникает в результате того, что индивидуальные значения признака складываются под совокупным влиянием разнообразных факторов (условий), которые по разному сочетаются в каждом отдельном случае.

Наличие вариации является основной предпосылкой статистического исследования. Варьирующие признаки могут быть количественными , если их варианты выражаются числовыми значениями (возраст, стаж работы, оплата труда и прочее) и неколичественными (атрибутивными), не имеющими числового выражения и представляющими собой смысловые понятия (профессия, социальная принадлежность и т д.)

Количественные признаки могут быть дискретными и непрерывными. Случаи, когда варианты признака могут принимать только одно из двух противоположных значений, говорят об альтернативном признаке. Признаки подразделяются на существенные, или главные, выражающие содержательную сторону явлений, и несущественные, или второстепенные, статистическому изучению подлежат существенные признаки.

Признаки, характеризующие статистическую совокупность, взаимосвязаны между собой, поэтому следует различать факторные (признаки-факторы) и результативные признаки.

Факторные признаки – это независимые признаки, оказывающие влияние на другие, связанные с ними признаки.

Результативные признаки – это зависимые признаки, которые изменяются под влиянием факторных признаков.

Итак, квалификация, стаж работы – это факторные признаки, а производительность труда – это результативный признак.

2. 1) Дисперсия постоянной величины равна нулю.

2) Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат.

3) Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин.

4) Дисперсия разности двух независимых случайных величин равна сумме дисперсий этих величин.

Справедливость этого равенства вытекает из свойства 2.

Теорема. Дисперсия числа появления события А в п независимых испытаний, в каждом из которых вероятность р появления события постоянна, равна произведению числа испытаний на вероятности появления и не появления события в каждом испытании.

3. Дисперсия, как и размах вариации, среднее линейное и среднее квадратическое отклонение относится к показателям вариации.

Дисперсия (D) признака определяется как средний квадрат отклонений вариантов от их средних значений, она рассчитывается по формулам простой и взвешенной (все зависит от исходных данных).

Формулу взвешенной D для вариационного ряда применяют при наличии у вариантов своих весов (также их называют частотами вариационного ряда).

Формулу для расчета простой преобразовывают и получают величину равную разности средней из квадратов вариантов (значений x) и квадрата их средней.

Расчет дисперсии по формулам не прост, а при больших значениях факторов (х) и частот (f) может быть очень большой.

Расчет дисперсии можно несколько упростить, если использовать её свойства (эти свойства доказываются в математической статистике). Таких основных свойств два: первое из которых гласит, что если абсолютно все значения признака (х) уменьшить (либо увеличить) на определенную постоянную величину С, то D при этом не изменится; второе свойство состоит в том, что если все значения фактора уменьшить (увеличить) в определенное число раз (A раз), то она уменьшится (увеличится) в A –квадрат раз.

6. Среди варьирующих признаков, которые изучает статистика, встречаются признаки вариации, которые проявляются в том, что у одних единиц совокупности они встречаются, у других нет. Признаки, которыми обладают данные единицы и не обладают другие, называются альтернативными. Количественно вариация альтернативного признака в численности всей совокупности обозначается а доля единиц, не обладающих признаком, обозначается и принимает значения.

Среднее значение альтернативного признака равно доле, которая является обобщающей характеристикой совокупности по этому варьирующему признаку. Тогда дисперсия альтернативного признака равна. Таким образом, дисперсия альтернативного признака равна произведению доли на дополняющее эту долю до единицы число. Т.к., , то средний квадрат отклонений не может быть больше 0,25.

Согласно правилу сложения дисперсий общая дисперсия равна сумме средней из внутригрупповых и межгрупповых дисперсий:

Смысл этого правила заключается в том, что общая дисперсия, которая возникает под влиянием всех факторов, равняется сумме дисперсий, которые возникают под влиянием всех прочих факторов, и дисперсии, возникающей за счет фактора группировки.

Пользуясь формулой сложения дисперсий, можно определить по двум известным дисперсиям третью неизвестную, а также судить о силе влияния группировочного признака.

7. Эмпирическое корреляционное отношение – это показатель тесноты связи между взаимосвязанными явлениями. η показывает степень тесноты связи между группировочным и результативным признаками. Значения коэффициента детерминации лежат в интервале от –1 до +1, то есть -1≤η≤+1.

При этом, если:

0,8≤| η|≤1, то связь тесная.

0,4≤| η|<0,8, то связь средняя

| η|<0,4, то связь слабая. ( По шкале Чеддока)

Семинарское занятие №7(2 часа)

Тема: Ряды распределения и их познавательные возможности

1. Понятие частоты и частности.

2. Понятие о закономерностях распределения.

3. Плотность распределения.

4. Изучение формы распределения.

5. Три типа распределений: симметричное, умеренно-асимметричное, крайне асимметричное.

6. Критерии согласия Пирсона, Романовского, Колмогорова, Ястремского.

7. Виды графиков и принципы их построения.

2. В процессе анализа статистических данных, представленных рядами распределения, кроме знания о характере распределения (или структуре совокупности) могут вычисляться различные статистические показатели (числовые характеристики), которые в обобщенном виде отражают особенности распределения изучаемых признаков. Наличие таких характеристик ( показателей) существенно облегчает сравнение различных распределений ( явлений) между собой.

Эти характеристики (показатели) могут быть разделены на 3 основные группы

1) характеристики центра распределения (средняя, мода, медиана);

2) характеристики степени вариации (вариационный размах, среднее линейное отклонение, дисперсия, среднее квадратическое отклонение, коэффициент вариации);

3) характеристики формы (типа) распределения (показатели эксцесса и асимметрии, ранговые характеристики, кривые распределения).

Первые две группы показателей будут рассмотрены в теме 8.В данном вопросе остановимся на знакомстве с основными понятиями и характеристиками третьей группы.

Полигоны и гистограммы в общем виде дают определенное представление о связи между частной (частностью) и величиной признака. Однако эмпирическое распределение признака, т.е. распределение в том виде, как оно получено в результате наблюдения, как правило, выявляет эту закономерность неясно. Ведь на значения признаков у единиц совокупности ( на индивидуальные значения) оказывают влияние различные случайные факторы. Более четкому выявлению закономерности распределения (т.е. закономерности изменения частот в вариационных рядах) способствует построение ряда с более крупными интервалами (или, что то же самое – с меньшим числом групп). Однако при слишком малом числе групп характерные особенности распределения также затушевываются.

3. Функция распределения полностью характеризует случайную величину, однако, имеет один недостаток. По функции распределения трудно судить о характере распределения случайной величины в небольшой окрестности той или иной точки числовой оси.

Определение. Плотностью распределения вероятностей непрерывной случайной величины Х называется функция f(x) – первая производная от функции распределения F(x).

Плотность распределения также называют дифференциальной функцией. Для описания дискретной случайной величины плотность распределения неприемлема.

Смысл плотности распределения состоит в том, что она показывает как часто появляется случайная величина Х в некоторой окрестности точки х при повторении опытов.

После введения функций распределения и плотности распределения можно дать следующее определение непрерывной случайной величины.

Определение. Случайная величина Х называется непрерывной, если ее функция распределения F(x) непрерывна на всей оси ОХ, а плотность распределения f(x) существует везде, за исключением( может быть, конечного числа точек.

Зная плотность распределения, можно вычислить вероятность того, что некоторая случайная величина Х примет значение, принадлежащее заданному интервалу.

Теорема. Вероятность того, что непрерывная случайная величина Х примет значение, принадлежащее интервалу (a, b), равна определенному интегралу от плотности распределения, взятому в пределах от a до b.

Доказательство этой теоремы основано на определении плотности распределения и третьем свойстве функции распределения, записанном выше.

Геометрически это означает, что вероятность того, что непрерывная случайная величина примет значение, принадлежащее интервалу (a, b), равна площади криволинейной трапеции, ограниченной осью ОХ, кривой распределения f(x) и прямыми x=a и x=b.

4. Основная задача анализа вариационных рядов – это выявление подлинной закономерности распределения, которая достигается увеличением объема исследуемой совокупности при одновременном уменьшении интервала ряда.

Из математической статистики известно, что если увеличить объем совокупности и уменьшить интервал группировки, изобразить эти данные графически, по полигон (гистограмма) распределения все более приближается к некоторой плавной линии, являющейся для него пределом и носящей название кривой распределения.

Под кривой распределения понимается графическое изображение в виде непрерывной линии изменения частот в вариационном ряду, функционально связанного с изменением вариант.

Получение кривой распределения на основе полигона или гистограммы можно представить лишь для гипотетического случая, соответствующего бесконечно большому числу единиц совокупности и бесконечно малой ширине интервала ряда. Только при этих идеализированных условиях кривая распределения представляет теоретическое распределение.

Теоретической кривой распределения называется кривая, выражающая общую закономерность данного типа распределения в чистом виде, исключающего влияние случайных для него закономерностей факторов. Но получение кривой распределения из эмпирических данных (полигон, гистограмма) возможно лишь для описанного идеального случая. Поэтому при проведении анализа вариационных рядов целесообразно свести эмпирическое распределение к одному из хорошо исследованных видов теоретического распределения.

Различают следующие разновидности кривых распределения:

1) одновершинные кривые: симметричные, умеренно асимметричные и крайне асимметричные;

2) многовершинные кривые.

6. Закон нормального распределения лежит в основе многих теорем и методов статистики при оценке репрезентативности выборки (расчете ошибки выборки и распространении характеристик выборки на генеральную совокупность); измерении степени тесноты связи и составлении модели регрессии; построении и использование статистических критериев и др. Как показывают многочисленные статистические исследования, частоты (частости) эмпирических распределений за редким исключением будут отличаться от значений теоретического распределения. Расхождения между частотами (частостями) эмпирического и теоретического распределения могут быть несущественными и объяснены случайностями выборки и существенными при несоответствии выбранного и эмпирического законов распределения.

Для проверки гипотезы о соответствии эмпирического распределения теоретическому закону нормального распределения используются особые статистические показатели-критерии согласия (или критерии соответствия). К ним относятся критерии Пирсона, Колмогорова, Романовского, Ястремского и др.

Большинство критериев согласия базируется на использовании отклонений эмпирических частот то теоретических. Очевидно, что чем больше эти отклонения, тем хуже теоретическое распределения соответствует (описывает) эмпирическому (эмпирическое). Статистические характеристики таких критериев согласия являются некоторыми функциями этих отклонений.

7. Статистический график - это чертеж, на котором статистические совокупности, характеризуемые определенными показателями, описываются с помощью условных геометрических образов или знаков.

Значение графического метода в анализе и обобщении данных велико. Графическое изображение, прежде всего, позволяет осуществить контроль достоверности статистических показателей, так как представленные на графике они делают более очевидными имеющиеся неточности, связанные либо с наличием ошибок наблюдения, либо с сущностью изучаемого явления. При построении графического изображения должен быть соблюден ряд требований. Прежде всего, графики должны быть достаточно наглядными, так как весь смысл графического изображения как метода анализа в том и состоит, чтобы наглядно изобразить статистические показатели. Кроме того, график должен быть выразительным, доходчивым и понятным. Чтобы все эти требования выполнялись, каждый график должен включать ряд основных элементов: графический образ; поле графика; пространственные ориентиры; масштабные ориентиры; экспликацию графика

Существует множество графических изображений. В основу их классификации может быть положен ряд признаков: а) способ построения графического образа; б) геометрические знаки, изображающие статистические показатели и отношения; в) задачи, решаемые с помощью графического изображения. По способу построения статистические графики делятся на диаграммы и статистические карты. Диаграммы - наиболее распространенный способ графических изображений. Диаграммы применяются для наглядного сопоставления в различных аспектах (пространственном, временном и др.) независимых друг от друга величин: территорий, населения и т.д. При построении точечных диаграмм в качестве графических изображений применяются совокупности точек; при построении линейных - применяются линии. Основной принцип построения всех плоскостных диаграмм сводится к тому, что статистические величины изображаются в виде геометрических фигур и, в свою очередь, подразделяются на столбиковые, полосовые, круговые, квадратные, фигурные. Статистические карты по графическому образу подразделяются на картограммы и картодиаграммы.

Семинарское занятие №8( 2 часа)

Тема: Техника выборочного наблюдения в статистике.

1. Виды выборки: собственно случайная, механическая, серийная, типологическая, многоступенчатая, моментная.

2. Генеральная и выборочная совокупность и их обобщающие характеристики.

3. Средняя и предельная ошибка выборочного наблюдения для показателей средней и для доли.

4. Повторный и бесповторный отбор.

5. Определение необходимой численности выборки.

6. Определение вероятности допустимой ошибки выборки.

7. Способы распространения данных выборочного наблюдения на генеральную совокупность.

8. Использование данных выборочного наблюдения для аналитических целей.

9. Понятие о малой выборке и определение ошибок при малой выборке.

1. виды выборки:

• собственно-случайная;

• механическая;

• типическая;

• серийная;

• комбинированная.

Собственно-случайная выборка заключается в отборе единиц из генеральной совокупности наугад или наудачу без каких-либо элементов системности. Однако прежде чем производить собственно-случайный отбор, необходимо убедиться, что все без исключения единицы генеральной совокупности имеют абсолютно равные шансы попадания в выборку, в списках или перечне отсутствуют пропуски, игнорирования отдельных единиц и т.п. Следует также установить четкие границы генеральной совокупности таким образом, чтобы включение или невключение в нее отдельных единиц не вызывало сомнений. Так, например, при обследовании студентов необходимо указать, будут ли приниматься во внимание лица, находящиеся в академическом отпуске, студенты негосударственных вузов, военных училищ и т.п.; при обследовании торговых предприятий важно определиться, включит ли генеральная совокупность торговые павильоны, коммерческие палатки и прочие подобные объекты.

Собственно-случайный отбор может быть как повторным, так и бесповторным. Для проведения бесповторного отбора в процессе жеребьевки выпавшие жребии обратно в исходную совокупность не возвращаются и в дальнейшем отборе не участвуют. При использовании таблиц случайных чисел бесповторность отбора достигается пропуском чисел в случае их повторения в выбранном столбце или столбцах.

Механическая выборка применяется в случаях, когда генеральная совокупность каким-либо образом упорядочена, т.е. имеется определенная последовательность в расположении единиц (табельные номера работников, списки избирателей, телефонные номера респондентов, номера домов и квартир и т.п.).

Генеральную совокупность при механическом отборе можно ранжировать или упорядочить по величине изучаемого или коррелирующего с ним признака, что позволит повысить репрезентативность выборки. Однако в этом случае возрастает опасность систематической ошибки, связанной с занижением значений изучаемого признака (если из каждого интервала регистрируется первое значение) или с его завышением (если из каждого интервала регистрируется последнее значение). Поэтому целесообразно отбор начинать с середины первого интервала

Типический отбор. Этот способ отбора используется в тех случаях, когда все единицы генеральной совокупности можно разбить на несколько типических групп. При обследовании населения такими группами могут быть, например, районы, социальные, возрастные или образовательные группы, при обследовании предприятий – отрасль или под-отрасль, форма собственности и т.п. Типический отбор предполагает выборку единиц из каждой типической группы собственно-случайным или механическим способом. Поскольку в выборочную совокупность в той или иной пропорции обязательно попадают представители всех групп, типизация генеральной совокупности позволяет исключить влияние межгрупповой дисперсии на среднюю ошибку выборки, которая в этом случае определяется только внутригрупповой вариацией.

Отбор единиц в типическую выборку может быть организован либо пропорционально объему типических групп, либо пропорционально внутригрупповой дифференциации признака.

Серийный отбор. Данный способ отбора удобен в тех случаях, когда единицы совокупности объединены в небольшие группы или серии. В качестве таких серий могут рассматриваться упаковки с определенным количеством готовой продукции, партии товара, студенческие группы, бригады и другие объединения. Сущность серийной выборки заключается в собственно-случайном или механическом отборе серий, внутри которых производится сплошное обследование единиц.

2. Пусть требуется изучить совокупность однородных объектов относительно некоторого качественного или количественного признака, характеризующего эти объекты. Например, если имеется партия деталей, то качественным признаком может служить стандартность детали, а количественным—контролируемый размер детали. Иногда проводят сплошное обследование, т. е. обследуют каждый из объектов совокупности относительно признака, которым интересуются. На практике, однако, сплошное обследование применяют сравнительно редко. Например, если совокупность содержит очень большое число объектов, то провести сплошное обследование физически невозможно. Если обследование объекта связано с его уничтожением или требует больших материальных затрат, то проводить сплошное обследование практически не имеет смысла. В таких случаях случайно отбирают из всей совокупности ограниченное число объектов и подвергают их изучению. Различают генеральную и выборочную совокупности:

Генеральной совокупностью называют совокупность всех мысленно возможных объектов данного вида, над которыми проводятся наблюдения с целью получения конкретных значений случайной величины, или совокупность результатов всех мыслимых наблюдений, проводимых в неизменных условиях над одной из случайных величин, связанных с данным видом объектов. Замечание: Часто генеральная совокупность содержит конечное число объектов. Однако если это число достаточно велико, то иногда в целях упрощения вычислений допускают, что генеральная совокупность состоит из бесчисленного множества объектов. Такое допущение оправдывается тем, что увеличение объема генеральной совокупности (достаточно большого объема) практически не сказывается на результатах обработки данных выборки. Выборочной совокупностью называют часть отобранных объектов из генеральной совокупности. Объемом совокупности (выборочной или генеральной) называют число объектов этой совокупности. Например, если из 1000 деталей отобрано для обследования 100 деталей, то объем генеральной совокупности N = 1000, а объем выборки п =100. Число объектов генеральной совокупности N значительно превосходит объем выборки n .

5. Одним из научных принципов в теории выборочного метода является обеспечение достаточного числа отобранных единиц. Теоретически необходимость соблюдения этого принципа представлена в доказательствах предельных теорем теории вероятностей, которые позволяют установить, какой объем единиц следует выбрать из генеральной совокупности, чтобы он был достаточным и обеспечивал репрезентативность выборки.

Уменьшение стандартной ошибки выборки, а следовательно, увеличение точности оценки всегда связано с увеличением объема выборки, поэтому уже на стадии организации выборочного наблюдения приходится решать вопрос о том, каков должен быть объем выборочной совокупности, чтобы была обеспечена требуемая точность результатов наблюдений. Расчет необходимого объема выборки строится с помощью формул, выведенных из формул предельных ошибок выборки (А), соответствующих тому или иному виду и способу отбора. Так, для случайного повторного объема выборки (n) имеем:

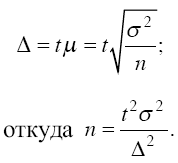
Суть этой формулы – в том, что при случайном повторном отборе необходимой численности объем выборки прямо пропорционален квадрату коэффициента доверия (t2) и дисперсии вариационного признака (?2) и обратно пропорционален квадрату предельной ошибки выборки (?2). В частности, с увеличением предельной ошибки в два раза необходимая численность выборки может быть уменьшена в четыре раза. Из трех параметров два (t и ?) задаются исследователем. При этом исследователь исходя из цели и задач выборочного обследования должен решить вопрос: в каком количественном сочетании лучше включить эти параметры для обеспечения оптимального варианта? В одном случае его может больше устраивать надежность полученных результатов (t), нежели мера точности (?), в другом – наоборот. Сложнее решить вопрос в отношении величины предельной ошибки выборки, так как этим показателем исследователь на стадии проектировки выборочного наблюдения не располагает, поэтому в практике принято задавать величину предельной ошибки выборки, как правило, в пределах до 10 % предполагаемого среднего уровня признака. К установлению предполагаемого среднего уровня можно подходить по разному: использовать данные подобных ранее проведенных обследований или же воспользоваться данными основы выборки и произвести небольшую пробную выборку.