Основные понятия и определения.

Криптология – это наука, состоящая из двух ветвей: криптографии и криптоанализа.

Криптография – это наука о способах преобразования (шифрования) информации с целью ее защиты от несанкционированных пользователей.

Криптоанализ – это наука (и практика ее применения) о методах и способах вскрытия шифров.

Открытый текст (ОТ) – это сообщение, предназначенное для пересылки.

Шифрованный текст (ШТ) – это замаскированное сообщение.

Открытый текст и шифрованный текст записываются с помощью конечного множества символов алфавита. Алфавиты могут не совпадать.

Термин буква или символ в алфавите может относиться не только к обычным буквам или цифрам, но и к любым знакам, используемым при записи сообщения.

Шифр – это способ преобразования открытого текста в шифрованный.

Шифрование – это процесс преобразования открытого текста в шифрованный текст.

Дешифрование – это процесс преобразования шифрованного текста в открытый текст.

Открытый текст и шифрованный текст разбиваются на элементарные сообщения (элементы). Элементом может быть одна буква, пара букв (биграмма), тройка букв (триграмма) и т.д.

Способность шифра противостоять различным атакам шифра называют стойкостью шифра.

Атака шифра - это попытка вскрытия шифра.

Канал атаки – это среда переноса от субъекта к объекту атаки (а возможно и наоборот), а также действий, осуществляющихся при проведении атаки.

Криптографически опасная информация – это информация о состоянии криптосредства, знания которой нарушителем позволит ему строить алгоритмы определения ключевой информации (или ее части) или алгоритм бесключевого чтения.

Криптосредство – это шифровальное (криптографическое) средство, предназначенное для защиты информации, не содержащей сведений, содержащих государственную тайну.

Под ключом криптографии понимают совокупность данных, обеспечивающих выбор одного конкретного криптографического преобразования из числа всех возможных в данной криптографической системе.

Ключ – это сменный элемент шифра, который применяется для шифрования конкретного сообщения.

Ключевая информация – это специальным образом организованная совокупность криптоключей, предназначенная для осуществления криптографической защиты информации в течение определенного срока.

Исходная информация – это совокупность данных, предназначенных для выработки по определенным правилам криптоключей.

Ключевой документ (ключевой шифр документа) – это физический носитель определенной структуры, содержащий ключевую информацию.

Ключевой блокнот – это набор бумажных ключевых документов одного вида, заброшюрованных и упакованных по определенным правилам.

Среда функционирования криптосредства – это совокупность технических и программных средств, совместно с которыми предполагается штатное функционирование криптосредства и которое способно повлиять на выполнение требований, предъявленных к криптосредству.

Модель нарушителя – это предположение о возможностях нарушителя, которые он может использовать для разработки и проведения атак, а так же об ограничения на эти возможности.

Модель угроз – это перечень возможных угроз.

История криптографии.

Уже в исторических документах древних цивилизаций Индии, Китая, Месопотамии имеются сведения о системах и способах представления шифрованного письма. Предполагается, что первые системы появились одновременно с письменностью в 4 тысячелетии до н.э.

В Древнеиндийских рукописях приводится более 60 способов письма, среди которых есть такие, которые можно рассматривать как криптографические. Например, есть описание системы замены гласных букв согласными и согласных букв гласными.

Один из сохранившихся шифрованных текстов Месопотамии представляет табличку, написанную клинописью и содержащую рецепт приготовления глазури для изготовления гончарных изделий. В табличке используются редко употребляемые значки, игнорировались некоторые буквы, употреблялись цифры вместо имен.

В рукописях Древнего Египта шифровались религиозные тексты и медицинские рецепты.

Шифрование использовалось также в Библии. Некоторые фрагменты текстов зашифрованы с помощью шифра атбаш. Правила шифрования заключалось в следующем: i-ая буква алфавита, где заменялось буквой с номером , где n – количество букв в алфавите.

В Древней Греции криптография уже широко использовалась во всех сферах жизни, особенно в государственной. Плутарх сообщает, что жрицы хранили в форме тайнописи свои прорицания. В Спарте в V-IV вв. до н.э. использовалось сцитало. Такой способ шифрования осуществлял перестановку букв в сообщении. Ключом шифра служил диаметр сцитала.

Другим шифровальным устройством в Спарте была табличка Энея. На небольшой табличке горизонтально располагался алфавит, а по бокам таблички имелись выемки для наматывания нити. При зашифровывании нить закреплялась у одной из сторон таблички и наматывалась на нее. На нити делались отметки (узелки) в местах, которые находились напротив букв данного текста. По алфавиту можно было двигаться лишь в одну сторону, делалось по отметке на каждом витке. После нить передавалась адресату. Этот шифр представляет шифр замены букв открытого текста знаками, которые обозначали расстояние между узелками. Ключом шифра являлась геометрия таблички и порядок букв на ней. Считалось, что это довольно надежный шифр.

Греческий писатель Полибий использовал систему сигнализации, которая была широко распространена как метод шифрования. Он записывал буквы алфавита в квадратную таблицу и заменял их координатами, парой чисел (i,j) – где i обозначало строку, а j – столбец. Применительно к латинскому алфавиту квадрат Полибия имеет вид:

	1	2	3	4	5
1	A	B	C	D	E
2	F	G	H	I, J	K
3	L	M	N	O	P
4	Q	R	S	T	U
5	V	W	X	Y	Z

Пары чисел (i, j) передавали с помощью факелов. Например, для того, чтобы передать букву “O”, нужно взять в правую руку 3 факела, а в левую – 4.

Подобные шифровальные приспособления существовали с небольшими изменениями до эпохи Юлия Цезаря. Однако положение меняется в эпоху расцвета Рима. Для того, что бы управлять наместниками в провинциях, шифровальная связь становится для римской власти жизненно необходимой. Особую роль сыграл способ шифрования, предложенных Юлием Цезарем, который был изложен им в «Записках о Галльской войне» (I в. до н.э.). Шифр Цезаря заключался в следующем: «… нужно читать каждый раз четвертую букву вместо первой, например, D вместо A, и т.д.». Таким образом, Цезарь заменял буквы в соответствии с подстановкой, нижняя строка которой представляет собой открытый текст, сдвинутый циклически на 3 буквы влево.

Научные методы в криптографии появились в арабских странах. Само слово «шифр» арабского происхождения (от арабского "цифра"; арабы первыми стали заменять буквы на цифры с целью защиты исходного текста).

Первая книга, посвященная описанию некоторых шифров, появилась в 885 году. Эта книга называлась «Книга о большом стремлении человека разгадать загадки древней письменности».

В 1412 году издается четырнадцати томная энциклопедия, содержащая системный обзор всех важнейших областей человеческих знаний. Называется она «Шауба аль-Аща», и ее автором является Шехаб аль-Камканди. В этой энциклопедии есть раздел о криптографии под заголовком «Относительно сокрытие в буквах тайных сообщений», в котором приводится семь способов шифрования. Там же дается перечень букв в порядке частоты их употребления в арабском языке на основе изучения текста Корана, а также приводятся примеры раскрытия шифров метом частотного анализа встречаемых букв.

В XIV веке появилась книга о системах тайнописи, написанная сотрудником тайной канцелярии Папы Римского Чикко Симонетти. В книге приводятся шифры замены, в которых гласным буквам соответствует несколько значковых выражений. Такие шифры называются шифрами многозначной замены или омофонами. Они получили развитие в XV веке. Так в книге «Трактат о шифрах», написанной секретарем Папы Клементия XV Габриелем де Лавиндо, приводится описание шифра пропорциональной замены, в котором каждой букве в соответствие ставится несколько эквивалентов, число которых пропорционально частоте встречаемости буквы в открытом тексте. В 1469 году был предложен подобный шифр, который назывался «Миланский ключ». Появление омофонов свидетельствовало о том, что к этому времени хорошо осознали слабости шифров простой замены. Такая модификация шифров разрушала статистику букв открытого сообщения, что явилось значительным шагом в развитии криптографии.

Еще одним значительным шагом в криптографии был сделан благодаря труду Леона Альберти. В 1466 году он написал труд о шифрах, в котором предложил шифр на основе шифровального диска. Устройство представляло собой пару соостных дисков разного диаметра, один из которых больше неподвижный. Окружности дисков разделены на 24 разных секторов, в которые вписаны буквы латинского алфавита в естественном порядке и четыре цифры, при этом из алфавита удалены четыре буквы, без которых можно обойтись. Имея два таких прибора, корреспонденты договаривались о первой индексной букве на подвижном диске. При шифровании отправитель ставил индексную букву против любой буквы большого диска. Он информировал о таком положении диска, записывая эту букву в качестве первой буквы шифрованного текста. Очередная буква открытого текста отыскивалась на неподвижном диске, а буква, стоящая напротив на подвижном диске, являлась буквой шифрованного текста. После нескольких букв (слов) положение индексной буквы менялось, о чем также передавалось корреспонденту. Такой метод имеет 2 особенности, которые делают это изобретение событием в развитии криптографии:

• в отличие от простой замены он использует не один, а несколько алфавитов для шифрования (это многоалфавитные шифры);

• шифровальный диск позволял использовать коды с перешифрованием, которые получили широкое распространение лишь в конце XIX века.

Для использования кодов с перешифрованием на внешнем диске имелись цифры. Альберти составлял код из 336 кодовых групп (от 11 до 4444). Каждому кодовому обозначению соответствовала законченная фраза. Когда такая фраза встречалась в сообщении, она замещалась соответствующим кодовым обозначением, а с помощью диска цифры зашифровывались как обычные знаки открытого текста, превращаясь в буквы.

Многоалфавитные шифры получили дальнейшее развитие в вышедшей в 1518 году первой печатной книге по криптографии под названием «Полиграфия». Автор книги – один из самых знаменитых ученых того времени аббат Иоганес Тритемий. В этой книге впервые в криптографии появилась квадратная таблица. Шифр-алфавиты записаны в строки таблицы один под другим, причем каждый из них сдвинут на 1 позицию влево по сравнению с предыдущим. Тритемий предлагал использовать эту таблицу для многоалфавитного зашифровывания самым простым способом. Первая буква текста шифруется первым алфавитом, вторая – вторым и т.д. В этой таблице не было отдельного алфавита открытого текста, это была первая строка таблицы.

Преимущество по сравнению с Альберти состоит в том, что с каждой буквой задается новый алфавит. Альберти же менял алфавиты лишь после трех или четырех слов. Поэтому его шифр текст состоит из отрезков, каждый из которых обладает закономерностью открытого текста, которая в свою очередь помогала вскрыть криптограмму. Побуквенное представление не дает такого преимущества.

Шифр Тритемия является первым нетривиальным примером периодического шифра. Так называется многоалфавитный шифр, правило зашифровывания которого состоит в использование периодически повторяющиеся последовательности простых замен.

В 1551 году Джованни Баттиста Белазо предложил использовать для многоалфавитного шифра буквенный легко запоминающийся ключ-пароль. Паролем могли быть слово или фраза. Пароль периодически записывался над открытым текстом. Буква пароля, располагающаяся над буквой открытого текста, указывала на алфавит таблицы, которая используется для зашифровывания этой буквы (по Тритемию). Белазо использовал обычные алфавиты.

Воскресил смешанные алфавиты, которые применял Альберти, а также объединил идеи Альберти с идеями Тритемия и Белазо в современную концепцию многоалфавитной замены итальянец Джованни де ла Порта. Ему было 28 лет, когда он в 1568 году опубликовал книгу «О тайной переписке». Эта книга явилась учебником по криптографии и содержала криптографические познания того времени. Порта предложил использовать квадратную таблицу с периодически сдвигаемым алфавитом и паролем. Он советовал выбирать длинный ключ.

Им также был предложен шифр простой биграммной замены. Пара букв заменялась графическим символом. Они заполняли квадратную таблицу 20*20, строки и столбцы которой занумеровывались буквами алфавита:

A B C D E F G H I L M N O P Q R S T U Z/

Например, биграмма EA зашифровывается как Δ, а LF –

В своей книге Порта ввел многоалфавитный шифр, которой можно представить в виде следующей таблицы, которая называется таблица Порта:

A B

a n

b o

c p

d q

e r

f s

g t

h u

i x

k y

l z

m w

C D

a o

b p

c q

d r

e s

f t

g u

h x

i y

k z

l w

m n

E F

a p

b q

c r

d s

e t

f u

g x

h y

i z

k w

l n

m o

G H

a q

b r

c s

d t

e u

f x

g y

h z

i w

k n

l o

m p

I K

a r

b s

c t

d u

e x

f y

g z

h w

i n

k o

l p

m q

L M

a s

b t

c u

d x

e y

f z

g w

h n

i o

k p

l q

m r

N O

a t

b u

c x

d y

e z

f w

g n

h o

i p

k q

l r

m s

P Q

a u

b x

c y

d z

e w

f n

g o

h p

i q

k r

l s

m t

R S

a x

b y

c z

d w

e n

f o

g p

h q

i r

k s

l t

m u

T U

a y

b z

c w

d n

e o

f p

g q

h r

i s

k t

l u

m x

X Y

a z

b w

c n

d o

e p

f q

g r

h s

i t

k u

l x

m y

Z W

a w

b n

c o

d p

e q

f r

g s

h t

i u

k x

l y

m z

Шифрование осуществляется при помощи лозунга, который пишется над открытым текстом. Буква лозунга определяет алфавит (заглавные буквы первого столбца). Расположенная под ней буква открытого текста ищется в верхнем или нижнем полуалфавите и замещается буквой второго полуалфавита.

Например, фраза начинающаяся со слов «HUNC CAVETO VIRUM» будет зашифрована с помощью лозунга «DE LA PORTA» во фразу «XFHP YTMOGA FQEAS».

Еще одно важное усовершенствование многоалфавитных систем, а именно использование в качестве ключа текста самого сообщения или шифрованного текста, принадлежит Джероламо Кардано и Блезу де Виженеру. Такой шифр был назван самоключом. В книге Виженера «Трактат о шифрах» самоключ представлен следующим образом. В простейшем случае основой является таблица Тритемия с добавлением к ней в качестве первой строки и первого столбца алфавита в естественном порядке. Такая таблица называется таблицей Виженера. В общем случае таблица Виженера состоит из циклически сдвигаемых алфавитов, причем первая строка может быть произвольным смешанным алфавитом. Первая строка – это алфавит открытого текста, а первый столбец – это алфавит ключа.

Для зашифровывания открытого сообщения Виженер предлагал в качестве ключевой последовательности Г использовать само сообщение с добавлением к нему в качестве первой буквы букву , известную отправителю и получателю. Этим идея Виженера отличалась от идеи Кардано, у которого не было начальной буквы, и система которого не обеспечивала однозначности расшифрования.

Последовательности букв подписывались друг под другом

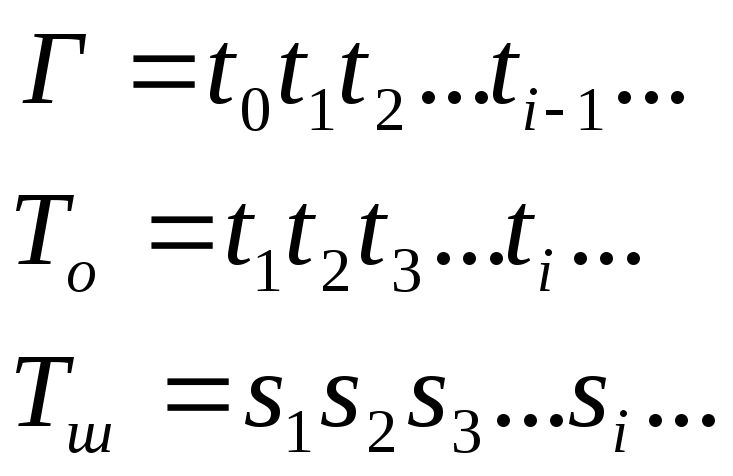
При этом пара букв друг под другом в Г и указывала номера строк и столбцов таблицы, на пересечении которых находится .

Например, фраза «HUNC CAVETO VIRUM» с начальной буквой P зашифровывается фразой «YCHP ECVWZH IDAMG».

Во втором варианте Виженер предлагал в качестве ключевой последовательности шифрованный текст.

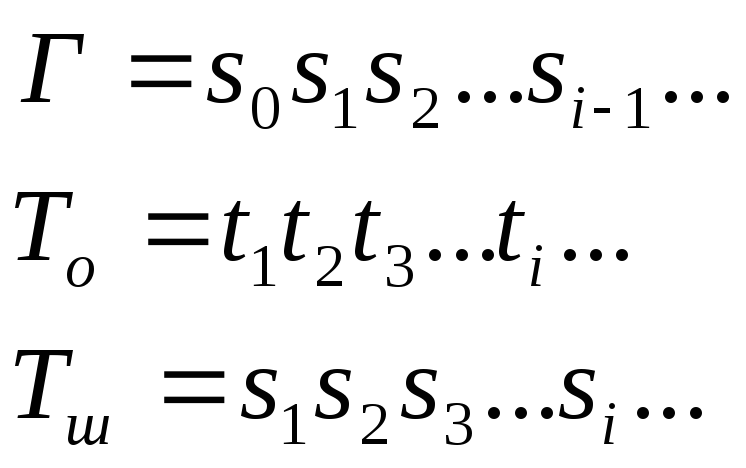
Самоключ Виженера был незаслуженно забыт, и под его шифром до сих пор понимают самый простой вариант с коротким ключевым словом и таблицей из обычных алфавитов.

Кардано принадлежит идея поворотной решетки, используемой в качестве средства шифрования. При помощи данной решетки стали применяться стенографические методы.

Стенография – это наука о методах и способах сокрытия факта наличия секретного сообщения.

Накладывая решетку на лист бумаги, в вырезах решетки записывалось сообщение, затем решетка снималась, и пространство заполнялось текстом. Такой способ шифрования использовали кардинал Ришелье и русский писатель Грибоедов. Ришелье использовал прямоугольник 7*10. Прорези размещались в позициях: (1;8), (2;9), (3;6), (4;5), (4;6), (5;1), (5;6), (5;7), (5;9), (6;2), (6;10), (7;9), (7;10)

Пример.

	1	2	3	4	5	6	7	8	9	10
1	I		L	O	V	E		Y	O	U
2	I		H	A	V	E		Y	O	U
3	D	E	E	P		U	N	D	E	R
4	M	Y		S	K	I	N		M	Y
5	L	O	V	E		L	A	S	T	S
6	F	O	R	E	V	E	R		I	N
7	H	Y	P	E	R	S	P	A	C	E

Кардано использовал квадратную решетку, которая своими вырезами покрывала всю площадь при ее совмещении. На основе таких решеток он построил шифр перестановки.

В начале XVII века Матео Ардженти, работавший в области криптографии, составил руководство по криптографии. В этой книге впервые было предложено использовать некоторое ключевое слово в качестве мнемонического ключа для смешанного алфавита. Началом смешанного алфавита служило ключевое слово (как правило, без повторяющихся букв), за которым следовали остальные буквы в естественном порядке. Например, на основе ключевого слова PIETRO можно составить следующий смешанный алфавит

P I E T R O A B C D E F G H L M N Q S U Z

Такие смешанные алфавиты использовались в качестве алфавита шифрованного текста в шифрах простой замены.

С целью усложнения шифра в шифр простой замены Ардженти вводил «пустышки», которые добавлялись в шифрованное сообщение, использовал шифрованные обозначения разной значности для некоторых частых сочетаний букв текста, вводил отдельные обозначения, придавал частым буквам несколько обозначений. Пример шифра Ардженти имеет следующий вид:

A	B	C	D	E	F	G	H	I	L	M	N	O
1	86	02	20	62 82	22	06	60	3	24	26	84	9
P	Q	R	S	T	U	Z	ET	CON	NON	CHE
66	68	28	42	80	04 40	88	08	64	00	44	5 7

В этом случае слово может быть зашифровано многими способами:

OT: ARGENTI

ШТ₁: 5128068285480377

ШТ₂:172850675628455803

Наибольшим достижением Ардженти считается разработанный им буквенный код – один из шифров замены, в котором буквы, слоги, слова и целые фразы заменялись группами букв.

В это же время в XVII-XVIII века в странах мира появляются «черные кабинеты». Это дешифровальные подразделения. Первый такой кабинет появился по инициативе кардинала Ришелье при дворе французского короля Людовика XIII. Его возглавил первый профессиональный криптограф Антуан Россиньоль. Отметим, что некоторые оригинальные идеи, возникшие в криптографии в это время, связаны с именем самого Ришелье. Он

использовал для тайной переписки с королем оригинальный шифр перестановки с переменным ключом.

Например,

ключ: 2741635; 15243; 671852493; 07; 28615; 943; 2741635; …

ОТ: LETTER SENT TO THE EMPEROR GIVING FULL DETAIL

ШТ: TLRTSEE ETOTN EPOEMTHER NI LUGIGVER TLIE SAD.

Известно также, что Ришелье пользовался и кодом.

Свой несложный код был и у Наполеона – малый шифр Наполеона. Он выглядел следующим образом:

A – 15, ar – 25, al - 29;

B – 37, bu – 3, bo – 35, bi – 29;

C – 6, ca – 32, ce – 20;

D – 3, de – 52;

E – 53, es – 82, et – 50, en – 68;

F – 55, fa – 69, fe – 58, fo – 71;

G – 81, ga – 51;

H – 85, hi – 77;

I – 119, jai – 122;

J – 87, jai – 123;

K - ?;

L – 96, lu – 103, le – 117, la – 106;

M – 114, ma – 107;

N – 115, ne – 94, ni – 116;

O – 90; ot – 153;

P – 137, po – 152;

Q – 173, que – 136;

R – 169, ra – 146, re – 126, ri – 148;

S – 167, sa – 171, se – 177, si – 134, so – 168, su – 174;

T – 176, ti – 145, to – 157;

U – 138;

V – 164, ve – 132, vi – 161, vo – 175;

W, X, Y - ?;

Z – 166.

В это же время в Европе получили широкое распространение шифры, названные номенклаторами, объединяющие в себе простую замену и код. В простейших номенклаторах код состоял из нескольких десятков слов или фраз с двумя буквенными и кодовыми обозначениями. Со временем списки заменяемых слов в номенклаторах выросли до 2-3 тысяч эквивалентных слов и слогов.

В России уже в XIV веке в Новгороде существовала техника тайного письма, где использовались шифры простой замены. Благодаря торговой связи Новгорода с Германией в России становятся известны новые западные разработки, в том числе и в сфере шифрования. Учреждение постоянной почтовой связи с Европой дало возможность развитию шифрованной переписки. Благодаря привлечению Петром I в Россию Готфрида Вильгельма Лейбница в Петербурге появляется цифирная палата, задачами которой было развитие и использование систем шифрования.

Когда Россиньоль начинал свою карьеру, номенклаторы как элемент открытого текста, так и кода располагались в алфавитном порядке (или еще в цифровом). Россиньоль заметил, что такой параллелизм открытого текста и кода облегчал восстановление открытого текста. Например, он установил, что если в английской депеше 137 обозначает for, а 168 – in, то он знал, что 21 не может заменять to, так как цифровые кодовые обозначения для слов, начинающихся с t, должны быть больше, чем начинающиеся с i. Обнаружив такую слабость, он перемешивал кодовые элементы по отношению к открытому тексту. На одном листе он располагал элементы открытого текста в алфавитном порядке, а кодовые в разбросанном, на другом листе – наоборот. Это явилось значительным шагом вперед в развитии криптографии.

В Англии тоже был свой «черный кабинет». В его работе в XVII в. заметное место занимал Джон Валлис, известный как крупнейший математик до Исаака Ньютона. Работы по вскрытию шифров для парламента привели к назначению Валлиса в 1649 году в Оксфорд профессором геометрии в возрасте 32 лет. В своем труде «Арифметика бесконечного» он сделал выводы, которые послужили Ньютону исходными для разработки интегрального исчисления. Валлис ввел знак для обозначения бесконечности, и первый, путем интерполяции, вычислил число .

В Германии начальником первого дешифровального отделения был граф Гронсфельд, создавший один из вариантов усовершенствованного шифра Виженера. Он взял числовой легко запоминающийся лозунг. Вместо таблицы Виженера использовался один несмешенный алфавит. При шифровании знаки открытого текста уписывались под цифрами лозунга. Очередная буква открытого текста заменялась буквой алфавита, отстоящая от нее вправо на соответствующее количество букв, равное цифре лозунга.

Пример:

От: GERMANY

Лозунг: 13579

Алфавит:

A	B	C	D	E	F	G	H	I	J	K	L	M
1	2	3	4	5	6	7	8	9	10	11	12	13
N	O	P	Q	R	S	T	U	V	W	X	Y	Z
14	15	16	17	18	19	20	21	22	23	24	25	26

Лозунг над текстом

1	3	5	7	9	1	3
G	E	R	M	A	N	Y

ШТ: HHWTJOB

Много новых идей в криптографии принес XIX в. Изобретение в середине XIX в. телеграфа и других технических средств связи дало новый толчок развитию криптографии. Информация передавалась в виде токовых и бестоковых посылок, т.е. представлялось в двоичном виде. Поэтому возникла проблема рационального представления информации, которая решалась с помощью кодов. Коды позволяли передавать длинное слово или целую фразу двумя или тремя знаками. Появилась потребность высокоскоростных способов шифрования и в коротких кодах, необходимых в связи с неизбежными ошибками при передаче сообщения. Однако еще до изобретения телеграфа появился ряд интересных шифровальных устройств.

Приблизительно в 1800 году была создана шифровальная система, занимающая особое место в криптографии, это дисковый шифратор Томаса Джеферсона – первого государственного секретаря США, ставшего в последующем третьим президентом.

Такая система имеет огромное количество ключевых элементов, к ним относятся: расположение букв алфавита на дисках, расстановка дисков на оси, выбор набора дисков из имеющегося запаса. Дисковый шифр можно отнести к типам многоалфавитных шифров, его особенностью является поблочный характер зашифровывания, при котором каждый участок текста (блок) зашифрован независимо от других, позже такие шифры начали называться поблочными шифрами.

В 1817 году другой американец Десиус Уодсворт сконструировал шифровальное устройство, которое использовало алфавиты открытого и шифрованного текста различной длины. Устройство, с помощью которого осуществлялось шифрование, представляло собой диск, на котором были расположены два подвижных кольца с алфавитами. Внешний алфавит состоял из 26 букв и 7 цифр (от 2 до 8), внутренний состоял из 26 букв. Диск имел подобие неподвижной часовой стрелки, в двух прорезях которой появлялось расположение друг под другом букв алфавита. На внутреннем кольце указывалась буква открытого текста, на внешнем – соответствующая буква шифрованного текста. Оба кольца могли вращаться и были связаны друг с другом. Буквы и цифры внешнего кольца были съемными и могли быть собраны в любом порядке. Перед зашифровыванием корреспонденты договаривались о взаимном расположении обоих колец. Такая шифровальная система реализует периодическую многоалфавитную замену. Различия чисел и букв алфавитов открытого и шифрованного текстов приводит к существенным отличиям от других шифровальных систем.

Уитстон изобрел шифр, который стали позже называть шифром Плейфера. В 1854 году Плейфер продемонстрировал систему шифрования, которую он назвал «недавно открытой симметричный шифр Уитстона». Это был первый из известных биграмных буквенных шифров. Этот шифр использовался англичанами в период первой мировой войны.

Во второй половине XIX века появился весьма устойчивый способ усложнения числовых кодов – гаммирование. Он заключался в перешифровании закодированного сообщения с помощью некоторого ключевого числа, которое называлось гаммой. Шифрование с помощью гаммы состояло в сложении всех кодовых групп в сообщении с одним и тем же числом. Эту операцию называли наложением гаммы. Например, 6413 – гамма, ШТ – 3425 7102 8139. Тогда результатом наложения гаммы будет являться следующая цифровая последовательность: 9838 3515 4552. Единица переноса, появляющаяся при сложении кодовых групп, опускалась. Снятие гаммы являлось обратной операцией, т.е. из результата вычиталась гамма.

В 1888 году француз маркиз де Виари в одной из своих научных статей, посвященных криптографии, обозначил греческой буквой «х» любую букву ШТ, греческой буквой «Г» – любую букву гаммы, и строчной буквой «с» – любую букву открытого текста. Используя эти обозначения, он по сути доказал, что алгебраическая формула (1) воспроизводит шифрование по Виженеру при замене букв алфавита числами, согласно следующей таблице:

A	B	C	D	E	F	G	H	I	J	K	L	M
0	1	2	3	4	5	6	7	8	9	10	11	12
N	O	P	Q	R	S	T	U	V	W	X	Y	Z
13	14	15	16	17	18	19	20	21	22	23	24	25

Тем самым была заложена алгебраическая основа для использования шифров замены типа шифра Виженера. Используя уравнение шифрования, можно было отказаться от громоздкой таблицы Виженера.

Позже лозунговая гамма стала произвольной последовательностью, а шифр с уравнением шифрования (1) стала называться шифром гаммирования.

Еще одним известным криптографом того времени был голландец Керкгоффс. Этот ученых написал книгу «Военная криптография», где были сформированы шесть требований к шифрам, 2 из которых относятся к стойкости шифрования, а остальные к эксплуатационным качествам шифра. Одно из них («компрометация системы не должна причинять неудобства корреспондентам») стала называться «правилом Керкгоффса». Суть правила состоит в том, что надежность системы определяется секретностью ключа.

В период первой Мировой войны в качестве полевых шифров использовались ручные шифры и в первую очередь шифры перестановки с различными усложнениями. Это были вертикальные перестановки, усложненные перекодировкой исходного алфавита, а также двойные вертикальные перестановки. Если до войны криптография представляла собой достаточно узкую область, то после войны она стала широким полем деятельности. Причина этого состояла в необычном росте объема шифра переписки. Криптоанализ стал важнейшим элементом разведки.

Прогресс в этот момент в области криптографии характеризуется изменениями в криптоанализе. Эта наука перестала быть уделом талантливых одиночек. Характер используемых шифров потребовал для их вскрытия скрупулезного анализа переписки, поиска ситуаций, благоприятных для криптоанализа, знаний, соответствующей обстановки. Кроме того, криптоанализ обогатился большим опытом использования в годы войны ошибок неопытных или ленивых шифровальщиков.

Последствия первой Мировой войны показали, что

1. Полностью исчерпало свои возможности ручное шифрование.

2. Полностью исчерпало свои возможности техническая сторона криптоанализа, состоящая в подсчете частоты встречаемых знаков.

В это время появляются криптографы Г.О. Ярдли, Г. Вернам и др.

С именем американца Вернама связан дальнейший успех в развитии криптографии. В 1917 г. он, будучи сотрудником телеграфной компании, предложил идею автоматического шифрования телеграфных сообщений. Речь шла о своеобразном наложении гаммы на знаки алфавита, представленные в соответствии с телетайпным кодом Бодо пятизначными индексными комбинациями. Например, буква «а» представлялась (++---), а (++-++) представлял собой переход от букв к цифрам. на бумажной ленте телетайпа знаку «+» соответствовало отверстие, а знаку «-» - его отсутствие. При считывании ленты металлические щупы проходили через отверстие, замыкали электрическую цепь и тем самым посылали в линию импульс тока. Вернам предложил электромеханически по-координатно складывать «импульсы» знаков открытого текста с «импульсами» гаммы, предварительно нанесенных на ленту. Сложение производилось по модулю 2. Предположим, например, знак открытого текста 11001 складывается со значением гамма 01111 и получается знак шифрованного текста 10110. Вернам сконструировал устройство для такого сложения. Замечательно то, что процесс шифрования в предложенной схеме оказался полностью автоматическим, т.е. исключался шифровальщик. Кроме того, оказались слитыми воедино процессы шифрования, расшифрования и передача данных по каналу связи. Было положено начало линейному шифрованию.

С 1917 по 1919 годы активно ведутся работы по созданию колесных шифраторов. Различные их конструкции были запатентованы примерно в одно и то же время в разных странах американцем М. Х. Хеберном, голландцем Х. Ф. Кохом, немцами А. Шербиусом и А. Г. Даммом. На основе этих дисков создавались шифровальные машины. Самая известная машина – это машина, созданная Шербиусом и названная «Энигма». Она в двух отношениях отличалась от других дисковых машин:

1. Ее устройство позволяло двойное шифрование каждой буквы;

2. Ее устройство позволяло неравномерное движение диска, которое управлялось зубчатыми колесами.

Шифрованное послание, закодированное «Энигмой», были раскодированы группой специалистов криптографов под руководством известного математика Тьюринга с помощью первой в истории вычислительной машины, сконструированной в 1942 году для перебора ключевых элементов.

Выдающиеся результаты в применении математических методов в криптографии принадлежат Клоду Шеннону. К 1944 году Шеннон завершил разработку теории секретной связи. В 1945 году им был подготовлен секретный доклад «Математическая теория криптографии», который был рассекречен в 1949 году и издан. В данной работе излагается теория секретных систем, служащих математической моделью шифров. Помимо основных алгебраических (или функциональных) свойств шифров, постулируемых в модели, множество сообщений и ключей наделяются соответствующими априорными вероятностными свойствами, что позволяет формализовать многие постановки задач синтеза и анализа шифров. В разработанной Шенноном концепции теоретической и практической секретности (стойкости) позволяется количественно оценивать криптографические качества шифров и пытаться построить в некотором смысле идеальные или совершенные шифры. Моделируется также язык открытых сообщений: предлагается рассматривать язык как вероятностный процесс, который создает дискретную последовательность символов с некоторой вероятностной схемой. Центральной в работах Шеннона является концепция избыточной информации, содержащаяся в текстовых сообщениях. Избыточность означает, что в сообщении содержится больше символов, чем в действительности требуется для передачи содержащейся в ней информации. Например, всего лишь 10 английских слов: the, of, and, to, a, in, that, it, is, why составляют более 25 процентов любого английского текста. Данные слова можно изъять из текста без потери информации, т.к. их легко можно восстановить по смыслу, или по контексту. Фактически Шеннон показал, что успех криптоанализа определяется тем, насколько избыточность, имеющаяся в сообщении, переносится в шифрованный текст. Если шифрование «стирает» избыточность, то восстановить текст по криптограмме становится принципиально невозможно.

Задачу дешифрования Шеннон рассматривает, как задачу вычисления апостериорных знаний противника о шифре после перехвата криптограммы. Понятие совершенной секретности Шеннон определяет требованием, чтобы апостериорные знания противника точно совпадали бы с априорными знаниями. В качестве примера совершенного шифра можно привести шифр Вернама со случайной равновероятной гаммой.

Теоретической мерой секретности или стойкости по Шеннону является энтропийная характеристика – неопределенность шифра по открытому сообщению, которое измеряет (в статистическом смысле) насколько «близка» средняя криптограмма из N букв единственному решению. Он выводит формулу для приблизительного вычисления минимального N, при котором находится единственное решение. Такая величина получила название расстояние единственности. Формула для расстояния единственности связывает между собой неопределенность шифров по открытому тексту и избыточность текста. Чем большим оказывалось расстояние единственности, тем больше шифр приближался к совершенному шифру, для которого расстояние единственности равно бесконечности.

Шеннон вводит понятие рабочей характеристики шифра, подходя к практической оценки стойкости. Он формулирует также основные оценки качества секретных систем с позиции практики их использования.

В работах Шеннона по исследованию свойств языка важнейшую роль играет величина удельной энтропии H на букву текста, т.е. среднее количество информации, переданной буквой открытого текста.

Работы Шеннона по исследованию свойств языка получили дальнейшее развитие в работах А. Н. Колмогорова, Б. Б. Пиотровского. Понятие «количество информации», содержащейся в тексте по Шеннону основывалось лишь на частотных характеристиках. В своих фундаментальных работах Колмогоров подошел к определению количества информации с учетом смыслового содержания текста.

Важную роль в исследовании данной проблемы сыграл выдающийся русский ученый А. А. Марков. Сегодня часто используются Марковские модели открытого текста, учитывающие зависимости букв текста от предыдущих букв.

Следующая страница в истории криптографии XX в. посвящена телефонным шифраторам, которые были разработаны в 30-х годах и стали широко использоваться во время второй Мировой войны. В России разработка телефонного шифратора велась под руководством Котельникова. Ему принадлежит значительная теорема дискретизации (теорема отсчетов), лежащая в основе цифровой обработке сигналов.

Идея телефонного шифратора была запатентована Д. Х. Роджерсом в 1881 году спустя 5 лет после изобретения Беллом телефоном. Идея состояла в передачи телефонного сообщения по нескольким цепям поочередными импульсами в некоторой быстро изменяющейся последовательности. Предполагалось разнести такие линии на значительные расстояния друг от друга для того, чтобы устранить возможность подключения по всем линиям сразу. Подключение к одной из них позволяло бы слышать отдельные неразборчивые сигналы.

В более поздних разработках предполагались различные преобразования самой речи. Звуки речи преобразуются телефоном в непрерывный элементарный сигнал, который с помощью соответствующих устройств изменялся шифратором по законам электричества. К числу возможных изменений относится: инверсия, смещение (или деление диапазона частот), шумовые маскировки, временные перестановки частей сигнала, а также различные комбинации указанных преобразований. Каждое из указанных преобразований производится под управлением ключа, который имеется у отправителя и получателя. Наиболее просто реализуемым являлось преобразование инверсии. Более сложными являлись временные перестановки. Для их осуществления речевой сигнал некоторый промежуток времени записывался на магнитной ленте. Запись делалась на отрезках длительностью в доли секунд. Отрезки с помощью нескольких магнитных головок разносились и перемещались, в результате чего в канале слышалась хаотическая последовательность звуков.

В США первый телефонный шифратор под названием «А-3» был принят в эксплуатацию в 1937 году.

В настоящее время аналоговая телефония уступает место цифровой телефонии, и соответственно многие технические проблемы, связанные с криптографическими преобразованиями цифрового шифрованного текста отпадают за ненадобностью.

Во второй половине XX в. вслед за развитием элементной базы вычислительной техники появились электронные шифраторы. Сегодня именно они составляют подавляющую долю средств шифрования. Прогресс в развитии вычислительной техники сделал возможными программные реализации криптографических алгоритмов.

В 70-х годах произошло 2 события, серьезно повлиявших на дальнейшее развитие криптографии. Во-первых, был принят и опубликован первый стандарт шифрования DES. Во-вторых, после работы двух американцев математика Диффи и Хеллмана появилась криптография с открытым ключом. Вслед за идеей Диффи и Хеллмана, связанной с гипотетическим понятием однонаправленной или односторонней функцией с секретом, появилась ее реализация – шифр-система RSA с открытым ключом. Такая система была предложена в 1988 году Райвестом, Шамиром и Адлеманом. Данный алгоритм для зашифрования и расшифрования использует новые ключи, причем ключ зашифрования может быть открытым, т.е. известным всем. В связи с несистемным использованием ключей алгоритмы, подобные RSA, стали называть ассиметричными шифр-системами, в то время как традиционные шифр-системы стали называть симметричными.

Наряду с идеей открытого шифрования Диффи и Хеллман предложили идею открытого распределения ключей, позволяющие избавится от защищенного канала связи при рассылке ключевой информации. Их идея основывалась на сложности решения задач дискретного логарифмирования, т.е. задачи, являющейся обратной для задачи возведения в степень конечном поле большого порядка.

Основные задачи защиты информации криптографическими методами.

Основная задача криптографии – защитить или сохранить в тайне необходимую информацию. Так как криптография дает средства для защиты информации, то она является частью деятельности по обеспечению безопасности информации. Криптография не «прячет» передаваемое значение, а преобразует его в форму недоступную для понимания противником.

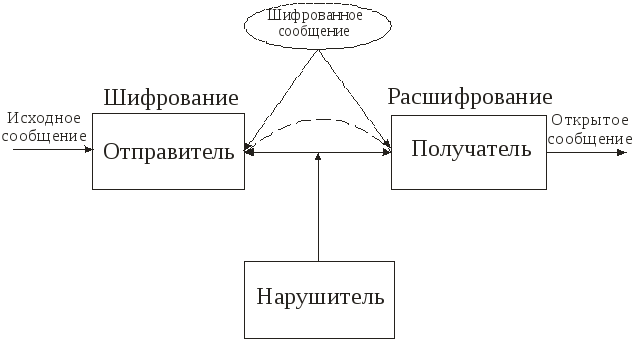
При этом исходят из предположения о полном контроле противником начала связи. Это означает, что нарушитель может не только пассивно перехватывать сообщения для дальнейшего анализа, но и активно изменять их, а так же отправлять поддельные сообщения от имени одного из абонентов. Помимо сохранения сообщения необходимо так же обеспечить достоверность полученной информации. Для решения этой задачи необходимо обеспечить:

1. проверку и подтверждение подлинности содержания и источника сообщения;

2. предотвращение и обнаружение обмана и других умышленных нарушений со стороны самих участников информационного обмена.

Для указанных целей так же используются криптографические методы защиты информации. Поэтому можно сказать, что современная криптография является областью знаний, связанной с решением таких проблем безопасности информации, как конфиденциальность, целостность, аутентификация и невозможность отказа сторон от авторства.

1. Обеспечение конфиденциальности – решение проблемы защиты информации от ознакомления с ее содержанием со стороны лиц, не имеющих права доступа к ней.

2. Обеспечение целостности – гарантирование не возможности несанкционированного изменения информации.

3. Обеспечение аутентификации – разработка и использование методов подтверждения подлинности сторон (идентификация) и самой информации в процессе информационного взаимодействия. Информация, передающаяся по каналу связи, может быть аутентифицирована по источнику, времени создания, содержанию данных, времени пересылки и т.д.

4. Обеспечение невозможности отказа от авторства – предотвращение возможности отказа субъектов от некоторых совершенных ими действий.

При использовании криптографических методов отправитель осуществляет преобразование (шифрование) исходной информации (открытой информации) в форму так называемого шифрованного текста.

Под нарушителем понимается любой субъект, не имеющий права ознакомления с содержанием передаваемой информации. Получатель получает шифрованное сообщение. Нарушитель пытается овладеть защищаемой информацией. Такие действия нарушителя называются атаками. Атаки могут быть пассивными и активными. Пассивные связаны со слежением, анализом трафика, перехватом записи передаваемых шифрованных сообщений, дешифрованием. При проведении активных атак нарушитель может прерывать процесс передачи сообщений, создавать поддельные или модифицировать передаваемые шифрованные сообщения. Эти активные действия называют попытками имитации и подмены соответствия.

Процесс шифрования однозначно определяется ключом и описывается некоторым криптографическим алгоритмом. Один и тот же криптографический может применяться для шифрования в различных режимах, тем самым реализуются различные способы шифрования. При расшифровании используется криптографический алгоритм, который в общем случае может отличаться от алгоритма используемого для шифрования сообщения. Соответственно могут различаться ключи зашифрования и расшифрования. Пару алгоритмов зашифрования и расшифрования называют криптосистемой (или шифр системы), а реализующие их устройства – шифротехникой. Если обозначить через М открытый текст, а через С – шифрованный текст, то процесс зашифрования и расшифрования можно записать в виде следующих равенств:

- зашифрование,

- расшифрование,

в котором алгоритмы зашифрования Е и расшифрования D должны удовлетворять равенству

.

Различают симметричные и ассиметричные криптосистемы. В симметричных системах знание ключа зашифрования позволяют легко найти ключ расшифрования (в большинстве случаев они совпадают). В ассиметричных криптосистемах знание ключа не позволяют определить ключ . Поэтому для симметричных криптосистем оба ключа должны быть секретными, а для ассиметричных – только один ключ – ключ расшифрования , а ключ можно сделать открытым. Поэтому такие системы называют системами с открытыми ключами.

Симметричные криптосистемы бывают поточными и блочными. Поточные осуществляют шифрование зашифрование отдельных символов открытого текста. Блочные производят зашифрование блоков фиксированной длины, состоящих из подряд идущих символов сообщений. Ассиметричные криптосистемы, как правило, являются блочными.

Не существует единого шифра, подходящего для всех случаев жизни. Выбор способов шифрования (криптографического алгоритма и режима его использования) зависит от особенности передаваемой информации, ее ценности, объема, способа представления, необходимой скорости передачи, а также возможности владельцев по защите своей информации (стоимость применяемых технических устройств и так далее).

Решение задачи целостности предполагает разработку средств, позволяющих обнаружить не только случайные искажения, но и целенаправленное навязывание противнику ложной информации. Для этого в передаваемую информацию внедряется избыточность. Как правило это достигается добавлением к сообщению некоторой проверочной комбинации, вычисляемой с помощью специального алгоритма и играющей роль контрольной суммы для проверки целостности полученного сообщения. Главное отличие такого метода от методов теории кодирования состоит в том, что алгоритм выработки проверочной комбинации является криптографическим, т.е. зависящим от некоторого секретного ключа. Без знаний секретного ключа вероятность успешного навязывания нарушителю ложной информации мала. Такая вероятность служит мерой имитостойкости шифра, т.е. способность самого шифра противостоять активным атакам со стороны противника. Т.е. для проверки целостности к сообщению М добавляется проверочная комбинация S, называемая кодом аутентификации или имитовставкой. В этом случае по каналу связи передаются сообщения . При получении сообщения получатель выясняет значение проверочной комбинации и сравнивает его с получением значения S. Несовпадение говорит и том, что данные были изменены.

Как правило, код аутентификации является значением некоторой зависимой от секретного ключа криптографической хэш-функции от данного сообщения

.

Хэш-функция – это функция, принимающая значения некоторой фиксированной размерности.

Кодам аутентификации предъявляются следующие требования:

1. невозможность вычисления значения S для заданного сообщения М без знания ключа ;

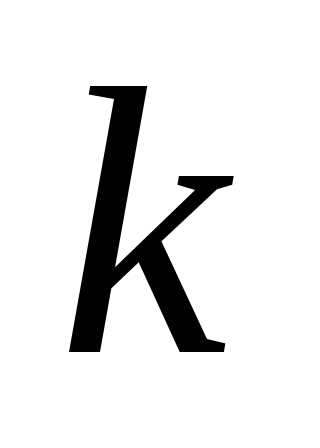2. невозможность подбора для заданного сообщения М с известным значением S другого сообщения 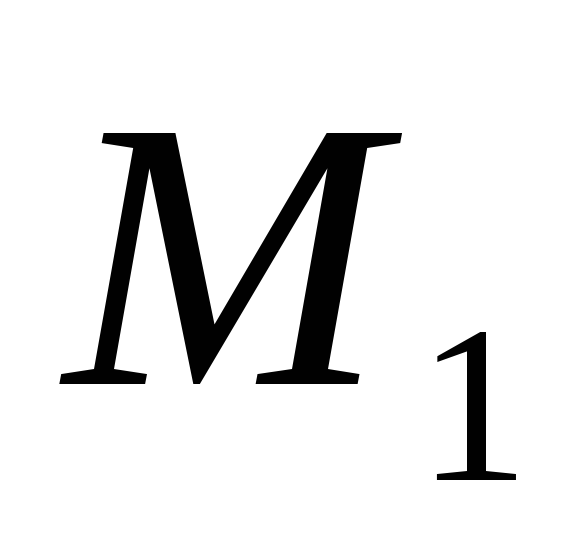с известным значением хэш-функции 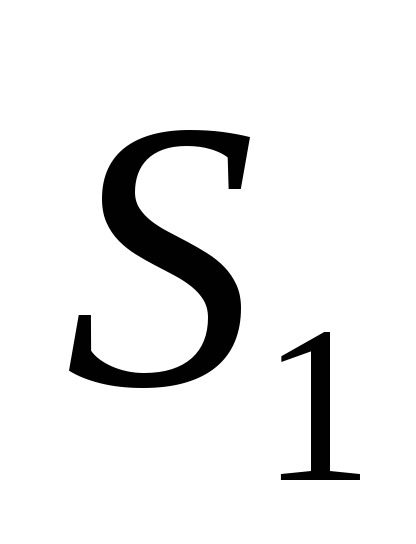без знания ключа .

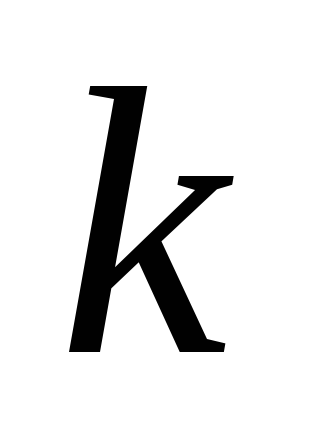Первое требование направлено против атак типа имитирования. Второе – против модификации передаваемых сообщений при атаках типа подмена.

Аутентификация.

Аутентификация - это установление подлинности. В общем случае этот термин может относиться ко всем аспектам информационного взаимодействия:

- к сеансу связи;

- к сторонам, передающим сообщения

- и т.д.

Применительно к сеансу связи аутентификация означает проверку:

- целостности соединения;

- невозможности повторной передачи данных противником;

- своевременность передачи данных.

Для этого используют дополнительные параметры, позволяющие «сцепить» передаваемые данные в легко проверяемую последовательность. Это достигается путем вставки в сообщение специальных чисел или меток времени. Они позволяют предотвратить попытки повторной передачи, изменение порядка следования или обратной отсылки части передаваемых сообщений. При этом такие вставки в передаваемом сообщении необходимо защищать (например, шифрованием) от возможных подделок и искажений.

Применительно к сторонам взаимодействия аутентификация означает проверку одной из сторон того, что взаимодействующая сторона именно та, за которую она себя выдает. Часто аутентификацию сторон называют идентификацией, хотя формально это не верно. Основным средством для проведения идентификации являются протоколы идентификации, позволяющие осуществлять идентификацию (и аутентификацию) каждой из участвующих во взаимодействии и не доверяющих друг другу сторон.

Различают протоколы односторонней и взаимной идентификации. Протокол – это распределительный алгоритм, определяющий последовательность действий каждой из сторон. В процессе выполнения протокола идентификации каждая из сторон не передает никакой информации о своем секретном ключе, а хранит его у себя и использует его для формирования ответных сообщений на запросы, поступающие при выполнении протокола. Применительно к самой информации аутентификация означает проверку того, что передаваемая по каналам связи информация является подлинной по содержанию, источнику, времени пересылки и т.д.

Проверка подлинности содержания информации сводится по сути к проверке ее неизменности с момента ее содержания в процессе передачи и хранения. Аутентификация источника данных подтверждения того, что исходных документ был создан именно заявленным источником.

Если стороны доверяют друг другу и обладают общим секретным ключом, то аутентификацию сторон можно обеспечить применением кода идентификации. Действительно, каждое успешно декодированное получателем сообщение может быть создано только отправителем, т.к. только они знают секретный ключ. Для недоверяющих сторон такое решение с использованием секретного ключа становится невозможным. Поэтому при аутентификации источника данных нужен механизм цифровой подписи.

В целом аутентификация источника данных выполняет ту же роль, что и протоколы идентификации. Отличие заключается только в том, что в первом случае некоторая передаваемая информация, авторство которой нужно установить, а во втором нужно установить сторону, с которой осуществляется взаимодействие.

Цифровая подпись.

Данный механизм используется в том случае, когда отдельные лица могут отказаться от ранее принятых обязательств. Например, отправитель может отказаться от факта передачи сообщения, утверждая, что его создал сам получатель (отказ от авторства). Получатель может легко модифицировать, подменить или создать новое сообщение, а затем утверждать, что оно получено от отправителя (приписывание авторства). В такой ситуации арбитр при решении спора не будет иметь возможности установить истину.

Основным механизмом в решении данной проблемы является цифровая подпись. Хотя цифровая подпись и имеет существенные отличия, связанные с возможностью отделения от документа и независимой передачей, а также возможностью подписывания одной подписью всех копий документа, она во многом аналогична обычной «ручной» подписи.

Схема цифровой подписи включает два алгоритма: для вычисления и для проверки.

Вычисление подписи может быть выполнено только автором подписи. Алгоритм проверки должен быть общедоступным, чтобы проверить подпись мог каждый. Для создания схемы цифровой подписи можно использовать симметричный шифр. В этом случае подписью может служить само зашифрованное на секретном ключе сообщение.

Но основной недостаток таких подписей состоит в том, что они являются одноразовыми. После каждой проверки секретный ключ становится известным. Единственных выход из этой ситуации в рамках использования симметричных шифр-систем – это введение доверительной третьей стороны, выполняющей функции посредника, которому доверяют обе стороны. В этом случае вся информация пересылается через посредника. Он осуществляет перешифрование сообщение одного из абонентов на ключ другого. Такая схема является крайне неудобной.

При использовании шифр-систем с открытым ключом возможны два подхода построения цифровой подписи:

1. преобразование сообщения в форму, по которой можно восстановить само сообщение и тем самым проверить правильность подписи;

2. в другом случае подписанное сообщение, как правило, имеет ту же длину, что и исходное сообщение.

Для создания такого подписанного сообщения можно осуществить шифрование на секретном ключе автора подписи. Тогда каждый может проверить правильность подписи путем расшифрования подписанного сообщения на открытом ключе автора подписи.

При втором подходе подпись вычисляется и передается вместе с исходным сообщением. Вычисление подписи заключается в преобразовании исходного сообщения в некоторую цифровую комбинацию, которая является цифровой подписью. Алгоритм вычисления подписи должен зависеть от секретного ключа пользователя. Это необходимо для того, что бы воспользоваться подписью мог только владелец ключа. В свою очередь алгоритм проверки правильности подписи должен быть доступен каждому. Поэтому этот алгоритм зависит от открытого ключа пользователя. В данном случае длинная подпись не зависит от длины подписи сообщения.

Одновременно с проблемой цифровой подписи возникла проблема построения бесконечных криптографических хеш-функций. Дело в том, что при вычислении цифровой подписи оказывается более удобным осуществлять сначала хеширование, т.е. свертку текста в некоторую комбинацию фиксированной длины, а затем подписывать полученную комбинацию с помощью полученного ключа. При этом функция хеширования, хотя и не зависит от ключа и является открытой, должна быть криптографической. Имеется в виду свойство односторонности этой функции: по значению комбинации свертки никто не должен иметь возможность подобрать исходное сообщение.

В настоящее время имеются стандарты на криптографические хеш-функции, утверждаемые независимо от стандартов на криптографические алгоритмы и цифровые подписи.

Управление секретными ключами.

Порядок использования криптографической системы определяется системами установки и управления ключами. Система установки ключей определяет алгоритмы процедуры генерации, распределения, передачи и проверки ключей. Система управления ключами определяет порядок использования, смены, хранения и архивации, резервного копирования и восстановления, замены или изъятия из обращения скомпрометированных, а также уничтожение старых ключей.

Предварительное распределение ключей.

Для надежной защиты информации, передаваемой по открытому каналу связи, применяют криптографические средства. Чтобы воспользоваться ими, необходимо осуществить первоначальный выбор и установку ключей. Выбранные ключи (сгенерированные) необходимо как-либо передать взаимодействующим сторонам. Поэтому для первичного распределения ключей необходим защищенный канал связи. Самый надежный способ первоначального распределения ключей – это личная встреча всех взаимодействующих сторон или использование специальных курьеров. Однако, при большом числе взаимодействующих сторон, требуется предварительная рассылка значительного объема ключевой информации и дальнейшего ее хранения. Поэтому на практике применяют специальные системы предварительного распределения ключей, предусматривающие распределение и хранение не самих ключей, а некоторой меньшей по объему информацией, по которой в дальнейшем каждая сторона может вычислить ключ для взаимодействия с другой стороны.

Система предварительного распределения ключей включает два алгоритма.

С помощью первого осуществляется генерация исходной информации. Эта информацию включает открытую информацию, которая будет передана всем сторонам или будет помещена на общедоступные серверы, и секретные части для каждой стороны.

Второй алгоритм предназначен для вычисления данного значения ключа для взаимодействия между абонентами по имеющейся у них секретной и общей ключевой информации.

Система предварительного распределения ключей должна быть устойчивой, т.е. учитывать возможность раскрытия ключевой части при компрометации, обмане и в сговоре абонентов, и гибкой, т.е. допускающей возможность быстрого восстановления путем исключения скомпрометированных и подключения новых абонентов.

Пересылка ключей.

После того, как предварительно распределение ключей произведено, может потребоваться передача ключей для каждого конкретного сеанса взаимодействия. Передача этих ключей может осуществляться с помощью шифрования и использования ранее полученных ключей.

Для передачи зашифрованных ключей по отрытому каналу связи между недоверяющими друг другу абонентами требуется решение всего комплекса задач по установлению подлинности различных аспектов взаимодействия, начиная от подлинности субъектов взаимодействия, подлинности передаваемых сообщений, подлинности самого сеанса связи и кончая подтверждением правильности (идентичности) полученных абонентами ключей.

Для центрального управления пересылками ключей создаются специальные доверительные центры, выполняющие функции центров распределения или перешифрования ключей. Различия между этими центрами заключаются в том, что в первом случае генерация ключей осуществляется в центре распределения, а во втором случае - самими абонентами.

Открытое распределение ключей.

Наиболее просто распределение ключей осуществляется в системах открытого распределения ключей. В предложенной Диффи и Хеллманом системе отрытого распределения ключей каждой из сторон имеет свой секретный параметр. Стороны реализуют определенный протокол взаимодействия по открытому каналу связи. При этом они обмениваются некоторыми сообщениям и по результатам этого обмена вычисляют общий секретный связной ключ.

В дальнейшем такие протоколы стали называть протоколами выработки общего ключа, т.к. изначально ни одна из сторон не имеет ключа и как такого распределения, пересылки в нем не происходит. В исходном виде система Диффи и Хеллмана обладала существенным недостатками, связанными с возможность для третьей стороны осуществления активного вхождения в канал связи и проведения полного контроля передаваемой информации. После внесения небольших модификаций и дополнений рассмотренный протокол позволяет осуществлять не только выработку общего ключа, но и одновременно проводить и подтверждать правильность вычислений, а также проверять взаимную аутентификацию сторон.

Схема разделения секрета.

Одной из задач современной криптографии, тесно связанной с проблемой распределения ключей, является задача построения схемы разделения секрета. Для многих практически важных приложений, связанных с запуском, или активацией критических процессов, или определяющих порядок получения доступа к значимым данным, ответственное лицо должно ввести секретный ключ. Чтобы обезопасить процедуру принятия решения и не отдавать все на волю одного человека, являющегося обладателем ключа, используют метод разделения секрета. Он состоит в назначении определенной группы лиц, которая имеет право принимать решения. Каждый член группы владеет определенной долей секрета (точнее специально выработанным набором данных, полная совокупность которых позволяет восстановить секретный ключ). При этом схема разделения секрета выбирается с таким условием, что для восстановления секретного ключа требуется обязательное присутствие всех членов группы, т.к. в случае отсутствия хотя бы одного из участников объединение долей оставшихся членов группы гарантировано не позволяет получить никакой информации о секретном ключе.

Таким образом, схема разделения секрета определяется двумя алгоритмами, удовлетворяющими выше сформулированному условию. Первый алгоритм определяет порядок вычисления значения долей по заданному значению секретного ключа, а второй предназначен для восстановления значения секрета по известным долям.

Задачу по построению схем разделения секрета можно обобщить:

- либо путем введения так называемых структур доступа, когда решение может приниматься не одной, а несколькими различными группами, причем часть из участников может наделяться правом вета;

- либо путем добавления механизмов, позволяющих обнаружить обман или сговор участников;

- либо введением специального протокола распределения долей между участниками с подтверждением правильности полученной информации и аутентификацией сторон.

Инфраструктура открытых ключей. Сертификаты.

Создание цифровой подписи позволило решить проблему сертификации открытых ключей. Она заключается в том, что перед тем как использовать открытый ключ некоторого абонента для отправки ему конфиденциального сообщения отправитель должен быть уверен, что открытый ключ действительно принадлежит этому абоненту.

Открытый ключ необходимо очень тщательно обезопасить, потому что если сервер, на котором они хранятся, не обеспечивает целостность и аутентичность, то злоумышленник имеет возможность подменить открытый ключ одного из абонентов и выступать от его имени. Поэтому для защиты открытых ключей создаются специальные центры сертификации, которые играют роль доверительной третьей стороны и заверяют открытые ключи каждого из абонентов своими цифровыми подписями.

Сертификат представляет собой набор данных, заверенный цифровой подписью центра и включающий открытый ключ и список дополнительных атрибутов, принадлежащих абоненту. К таким атрибутам относятся имена пользователя и центра сертификации, номер сертификата, время действия сертификата, предназначение открытого ключа и т.д.

Международный стандарт ISO X.509 определяет общую структуру сертификатов открытых ключей и протокол их использования для аутентификации в распределенных системах.

Центры сертификации.

Центр сертификации предназначен для регистрации абонентов, изготовления сертификатов открытых ключей, хранение изготовленных сертификатов, поддержание в активном состоянии справочника действительных сертификатов.

Для сетей с большим числом абонентов создается несколько центров сертификации. Центры сертификации объединяются в древовидную структуру, в корне которой находится главный центр сертификации, который выдает сертификаты подчиненным ему отраслевым центрам, обеспечивая доверие к открытым ключам этих центров. Каждый центр вышестоящего уровня аналогично делегирует право выпуска сертификатов подчиненным ему центрам. В результате доверие сертификата открытого ключа каждого центра основано на заверении его сертификата ключом вышестоящего центра. Сертификаты главного центра подписывает сам главный центр. Зная иерархию и подчиненность друг другу центров сертификации, можно всегда точно установить, является ли абонент владельцем данного открытого ключа.

Основная трудность при создании центров сертификации заключается в их юридическом статусе и потенциальных финансовых возможностях по выплатам компенсации за ущерб, понесенный в результате невыполнения подписанных цифровыми подписями с использованием сертификатов, выданных этим центром, договоров и контрактов, сорванных по причине отказа от цифровых подписей или их подделке.

Обозначения.

- множество слов в алфавите .

- мощность множества .

- абсолютная величина числа .

- целая часть числа .

- ближнее целое число не меньше .

- сравнимость чисел и по модулю .

- остаток от деления числа на число .

- множество с бинарной операцией *.

- правило зашифрования (расшифрования) на ключе .

- правило зашифрования на ключе сообщения, образованного приписыванием сообщений друг к другу.

- значение хеш-функции для последовательности, образованной приписыванием последовательностей друг к другу.

- конечное поле из элементов.

- симметричная группа подстановок на множестве , где .

- функция «след» из конечного поля в конечное поле , с другой стороны эта функция равна .

- множество , образующее кольцо относительно сложения и умножения по модулю .

- множество образующих элементов кольца .