§4.4. Метад рацыяналізацыі.
def
Мнагаскладам ступені
ад дзвюх зменных
і
называецца выраз
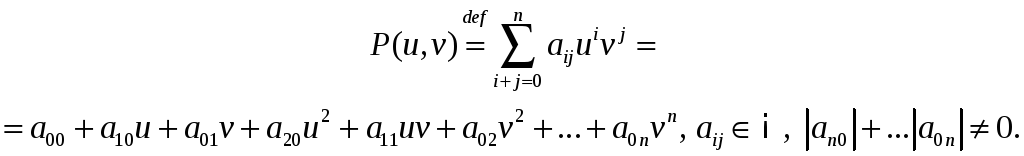
Рацыянальнай
функцыяй дзвюх зменных называецца выраз
дзе
– мнагасклады.
Зазначым
пры гэтым, што складаная функцыя
,
дзе
– рацыянальныя функцыі, ёсць таксама
рацыянальная функцыя.
1º. Інтэграванне дробава-лінейнай ірацыянальнасці.
Будзем разглядаць інтэгралы тыпу
,
г. зн.
.
Зробім
замену
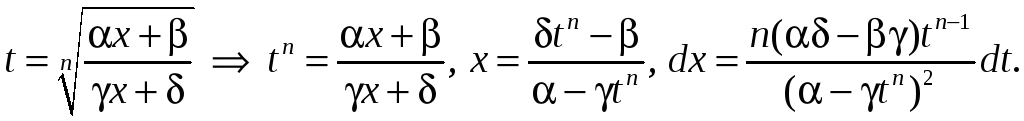
Маем
Прыклад
1.
Вылічыць
.
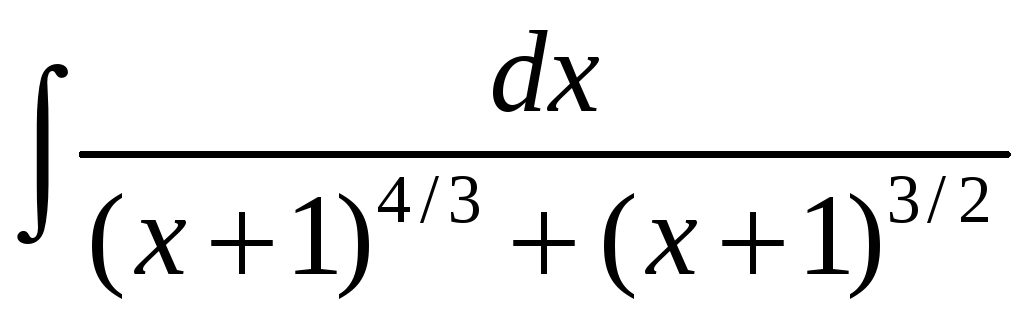► Спачатку зробім наступнае пераўтварэнне падынтэгральнай функцыі
.
Пасля
гэтага зробім замену
.
Маем
Падынтэгральную функцыю раскладзем на суму простых дробаў
.
Метадам
дамнажэння вылічаем
.
Надаючы прыватныя значэнні
і
,
атрымаем
,
.
Адкуль
Маем
.
Такім
чынам,
.
◄
2º. Інтэграванне біномнага дыферэнцыяла.
Пры
вылічэнні інтэграла
маюць месца тры выпадкі інтэгравальнасці.
1) 
.
Няхай пры гэтым
.
Падынтэгральная функцыя ёсць
дробава-лінейная ірацыянальнасць
,
дзе
– найменшы супольны кратны назоўнікаў
лікаў
і
.
Падстанова
рацыяналізуе падынтэгральную функ-цыю.
2) 
.
Зробім замену
і атрымаем
.
Калі
,
то падынтэгральная функцыя ёсць
дробава-лінейная ірацыянальнасць
,
а таму падстанова
рацы-яналізуе інтэграл ад апошняй
функцыі. Такім чынам, падстанова
рацыяналізуе зыходны інтэграл. Пры
гэтым сам інтэграл мае выгляд
3) 
.
Пасля замены
атрымаем інтэграл
.
Падынтэгральная функцыя ёсць
,
дзе
– назоўнік рацыянальнага ліку
.
Такім чынам, падстанова
рацыяналізуе інтэграл у гэтым выпадку.
Расійскі матэматык Чабышоў даказаў, што ў іншых выпадках інтэграл не вылічаецца ў элементарных функцыях.
Назавем іншыя інтэгралы, якія не вылічаюцца ў элементарных функцыях.
– інтэграл
Пуасона;
– інтэгралы Фрэнэля;
– інтэгральны
лагарыфм;
– інтэгралы Дырыхле.
3º. Інтэграванне рацыянальна-трыганаметрычных функцый.
Інтэгралы
тыпу
заўсёды рацыяналізуюцца універсальнай
падстановай
.
Сапраўды
У некаторых прыватных выпадках вылічэнне інтэгралаў ад рацыянальна-трыганаметрычных функцый праводзіцца пры дапамозе больш зручных падстановаў.
а)
Калі
,
то інтэграл рацыяналізуецца падста-новаю
б)
Калі
,
то інтэграл рацыяналізуецца падста-новаю
в)
Калі
,
то інтэграл рацыяналізуецца падста-новаю
Прыклад 2.
.
Падынтэгральную
функцыю раскладзем на суму простых
дробаў з нявызнача-нымі каэфіцыентамі
і метадам дамнажэння атрымаем
Прыклад
3. Інтэграл
не падпадае ні пад адзін прыватны
выпадак. Таму робім універсальную
падстанову
.
=
=
=
=
.
4º. Інтэграванне квадратовых ірацыянальнасцяў.
Будзем
разглядаць інтэгралы тыпу
1) Калі
,
то
,
г. зн. што падінтэгральная функцыя
ёсць рацыянальная функцыя .
2) Калі
,
то
,
г. зн. падінтэгральная функцыя ёсць
дробава-лінейная ірацыянальнасць.
3) Калі
ж
,
то
,
бо пры
не існуе
.
Пры гэтым выкарыстоўваюць падстановы
Ойлера:
,
або
.
Прыклад
4.
Вылічыць
.
►Выканаем
першую падстанову Ойлера
,
прычым выбіраем знак “–“, паколькі
пры гэтым
.
Далей маем
.
=
◄
Падстановы
Ойлера часта прыводзяць да складаных
выкладак. У многіх выпадках квадратовыя
ірацыянальнасці можна праінтэграваць
метадам нявызнычаных каэфіцыентаў.
Напрыклад, інтэграл
,
дзе
– мнагасклад, вылічаюць метадам
нявызначаных каэфіцыентаў паводле
формулы
дзе
– мнагасклад ступені
з нявызначанымі каэфіцыентамі,
– невядомая канстанта. Пасля дыферэнцавання
гэтай роўнасці атрымаем
Дамнажаючы
абедзве часткі на
,
прыходзім да роўнасці
Метадам
адпаведных каэфіцыентаў знойдзем
мнагасклад
і лік
.
Прыклад
5.
Вылічыць
.
► Правядзем вылічэнне інтэграла метадам нявызначаных каэфіцыентаў.
Пасля дыферэнцавання маем
Дамнажаючы
абедзве часткі роўнасці на
,
маем
Метадам адпаведных каэфіцыентаў прыходзім да сістэмы:
Такім
чынам,
