Раздзел 4. Інтэгральнае злічэнне. §4.1. Азначэнне і ўласцівасці нявызначанага інтэграла.

Асноўнаю задачай дыферэнцыяльнага злічэння ёсць знаходжанне вытворнай дадзенай функцыі. Пры разгледжанні многіх пытанняў як матэматыкі, так і яе дастасаванняў узнікае адваротная задача: для дадзенай функцыі знайсці такую функцыю , каб . Аднаўленне функцыі па зададзенай яе вытворнай ёсць асноўная задача інтэгральнага злічэння.

1° Азначэнне нявызначанага інтэграла.

def. Дыферэнцавальная на інтэрвале Х функцыя называецца першаіснаю для функцыі на Х, калі .

Тэарэма 1 (пра агульны выгляд першаіснай). Няхай функцыя ёсць першаісная для на х. Функцыя ёсць таксама першаісная для , калі і толькі калі .

□ 1)(Неабходнасць). Няхай таксама першаісная для , г. зн. і , або . Згодна з тэарэмаю пра супаданыя вытворныя .

2)(Дастатковасць). Няхай . Паколькі , то

, г. зн. – першаісная для . ■

Такім чынам, для дадзенай функцыі яе першаісная вызначаецца неадназначна, менавіта з дакладнасцю да сталага складніка. Для таго каб з сям’і першаісных вылучыць пэўную першаісную , дастаткова задаць пункт , які належыць графіку функцыі .

def. Калі ёсць першаісная для на інтэрвале Х , то сукупнасць першаісных для называюць нявызначаным інтэгралам ад функцыі на Х і абазначаюць

. (1)

У гэтым абазначэнні знак называецца знакам інтэграла, – падінтэгральнай функцыяй, а – падінтэгральным выразам. Аперацыю знаходжання нявызначанага інтэграла ад дадзенай функцыі называюць інтэграваннем. Яна ёсць адваротная да аперацыі дыферэнцавання.

Падінтэгральны выраз можна запісваць некалькімі спосабамі

. (2)

2° Уласцівасці нявызначанага інтэграла.

1º.

□ ■

2º.

□ ■

3º.

□ Паколькі , то . З друго-га боку . Правыя часткі апошніх дзвюх роўнасцяў супадаюць, калі . Паколькі , то па зададзеным ліку можна знайсці лік і, наадварот, па зададзеным ліку можна знайсці лік . ■

4º. .

□ Калі , то

. ■

З уласцівасцяў 3º. і 4º. вынікае, што аперацыя інтэгравання мае ўласцівасць лінейнасці:

.

На падставе табліцы вытворных атрымаем табліцу нявызначаных інтэгралаў:

Ведаючы табліцу і ўласцівасці нявызначанага інтэграла, можна вылічаць інтэгралы ад некаторых функцый.

Прыклад 1.

.

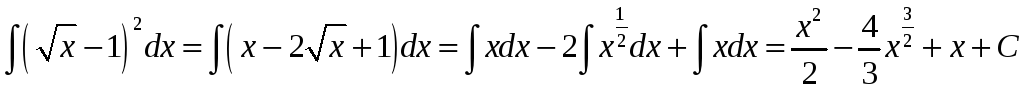Прыклад 2. .

§4.2. Асноўныя метады інтэгравання.

1º. Метад падстановы.

У многіх выпадках увядзенне новай зменнай інтэгравання дае магчымасць звесці вылічэнне дадзенага інтэграла да табліцавага. Такі метад інтэгравання называецца метадам падстановы або метадам замены зменнай і выкарыстанне яго грунтуецца на наступнай тэарэме.