Занятие 9. Доказательство пределов. Задачи

9.1. 1) Докажите, что . 2) Обобщите полученный результат, доказав, что .

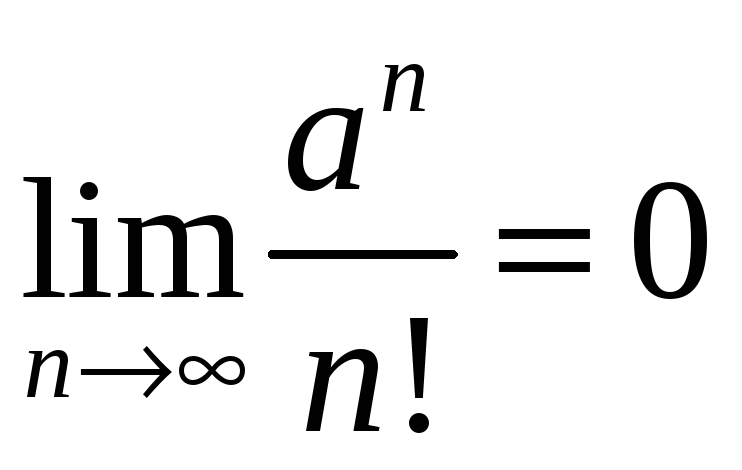
9.1. 1) Докажите, что . 2) Обобщите полученный результат, доказав, что .

9.2. Докажите .

9.3. Докажите .

9.4. 1) Докажите ; 2) Вычислите .

9.5. 1) Пусть и Докажите, что . 2) Найдите .

9.6. Найдите пределы последовательностей : 1) , где – многочлен степени , причём ;

2) .

9.7. Найдите: 1) ; 2) ;3) ; 4) .

9.8. Докажите сходимость монотонных последовательностей: 1) ; 2) .

9.9. С помощью Критерия Коши докажите сходимость последовательности , т.е. сходимость ряда .

9.10. Сформулируйте в положительном смысле, что данная последовательность не удовлетворяет условия критерия Коши. Докажите расходимость ряда .

Домашнее задание 9.

9.11. Докажите 1) ; 2) .

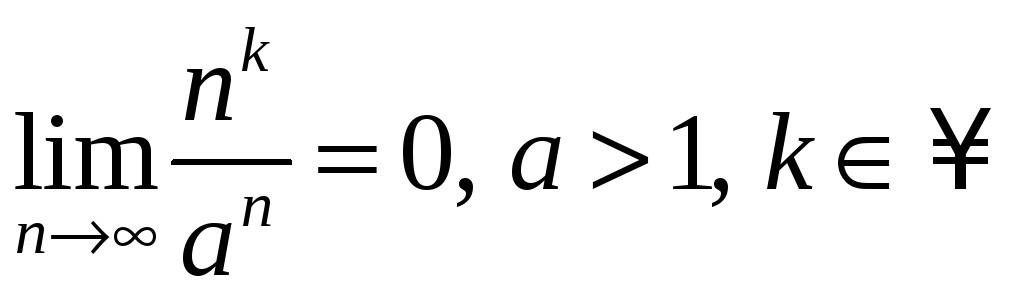9.12. Найдите пределы последовательностей : 1) ; 2)  где .

9.13. Докажите сходимость монотонных последовательностей: 1) ; 2)  где ограниченная последовательность с положительными членами.

9.14. С помощью Критерия Коши докажите сходимость последовательности .

Занятие 10. Контрольная работа №1. Самоподготовка.

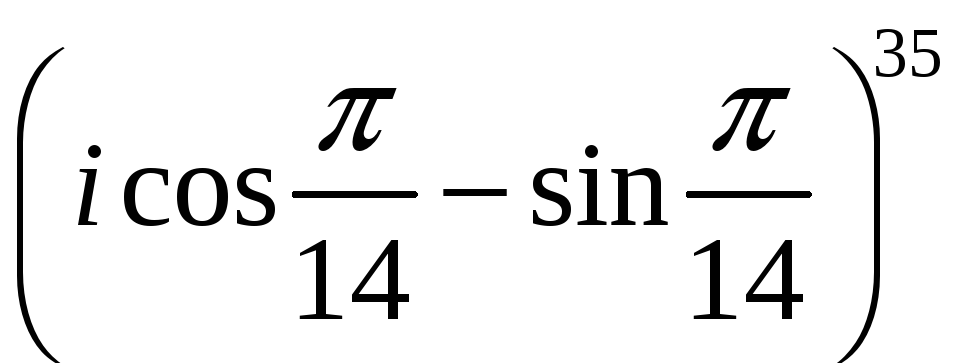1. Вычислите а) ; б) ;в) .

2. Найдите коэффициент при разложения бинома .

3. Найдите а) комплексные корни уравнения ; б) найменьший действительный корень многочлена , если он имеет корень . в) действительные корни многочлена , если известно, что он делится на двучлен .

4. Пользуясь определением предела, докажите, что: а) 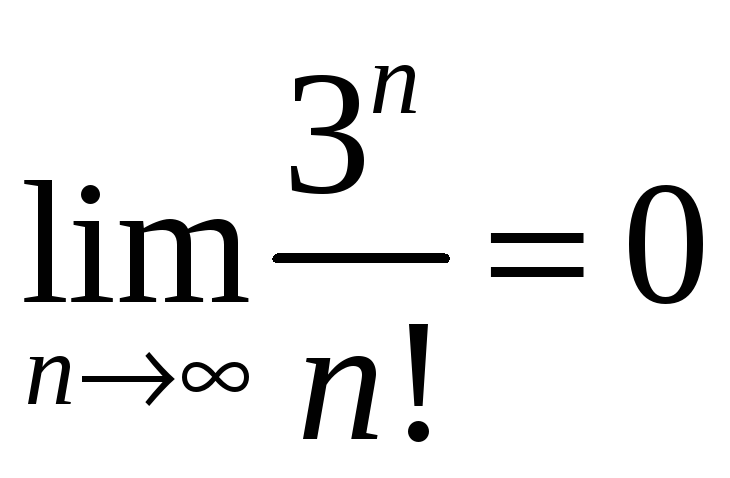; б) ; в) ; г) .

5. Вычислите: а) ; б) ; в) ; г) ; д) .

Занятие 11. Предел функции. Задачи

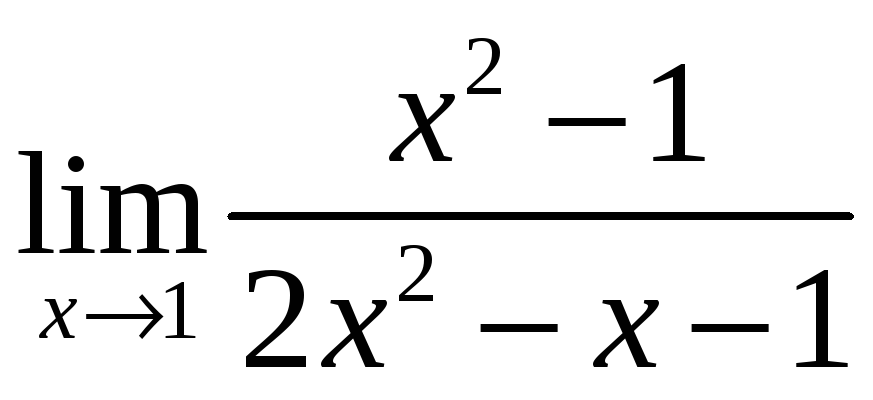11.1. Найдите пределы: 1) ; 2) ; 3) .

11.2. Найдите пределы: 1) 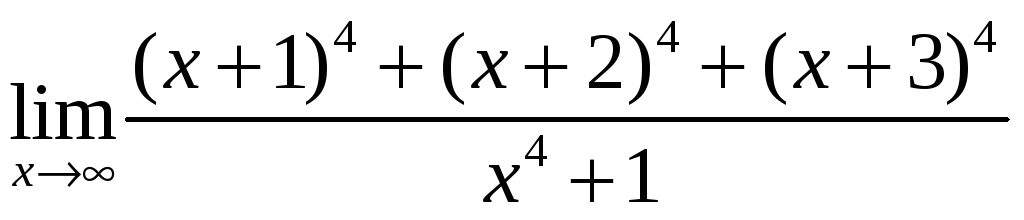 ; 2) ; 3) .

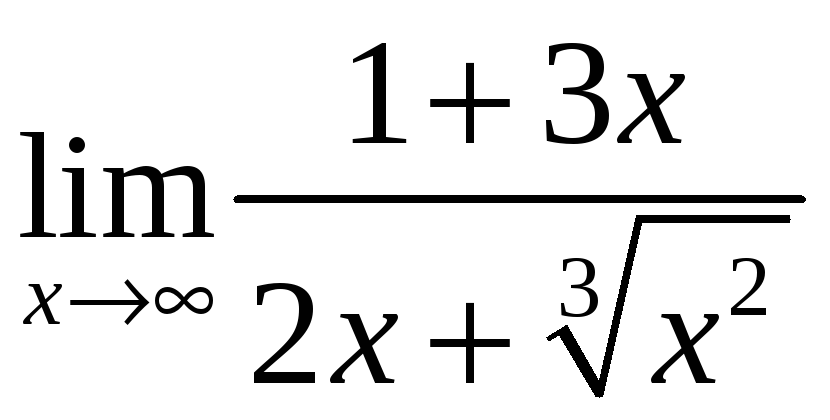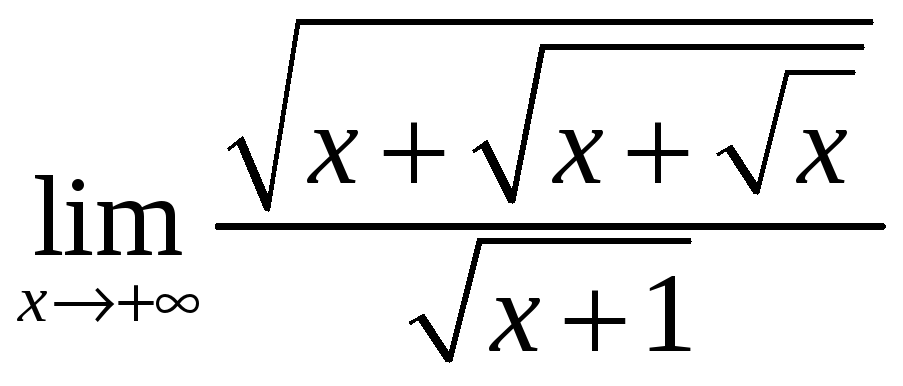11.3. Найдите пределы: 1); ; 2) ; 3) ; 4) .

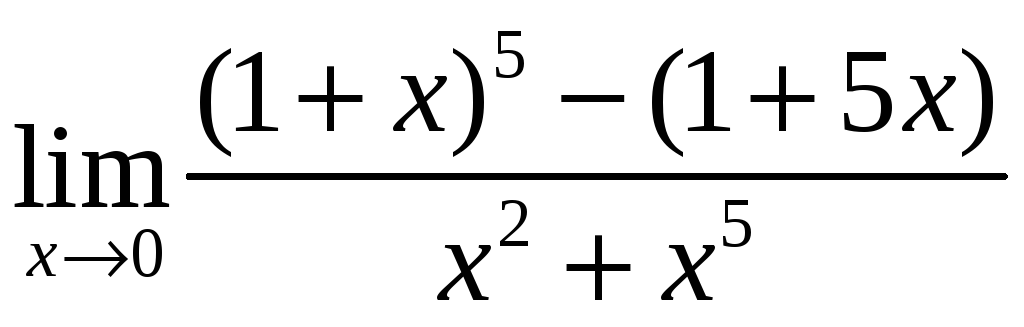11.4. Найдите пределы: 1) ; 2) ; 3)

11.5. Найдите пределы: 1)  ; 2)

11.6. Найдите пределы: 1)  ; 2) . 3) ; 4) .

11.7. Найдите предел .

Домашнее задание 11.

11.8. Найдите пределы: 1) ; 2) .

11.9. Найдите пределы: 1) ; 2) ; 3) .

11.10. Найдите пределы: 1) ; 2) .

11.11. Найдите пределы: 1) ; 2) ; 3) .

11.12. Найдите пределы: 1) ; 2) ; 3) .

Занятие 12. Замечательные пределы.

Задачи

12.1. Найдите пределы: 1) 2) 3) 4) .

12.2. Найдите пределы: 1) 2) 3) .

12.3. Найдите предел .

12.4. Найдите пределы: 1) ; 2) .

12.5. Найдите пределы: 1) ; 2) ; 3) .

12.6. Найдите пределы: 1) ; 2) .

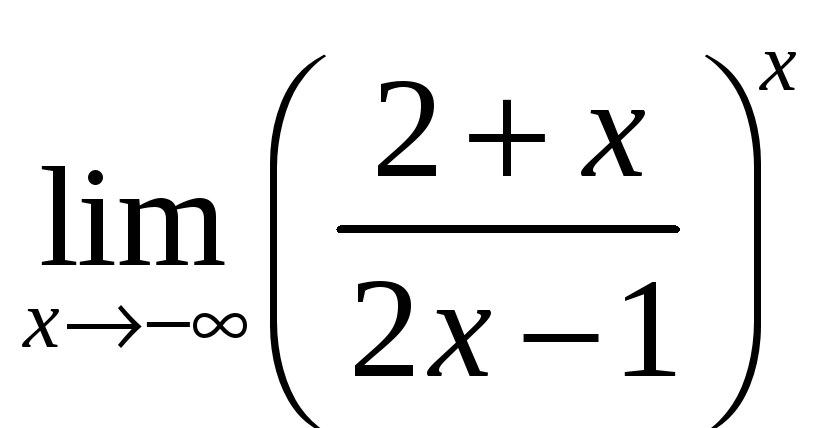12.7. Найдите пределы: 1) ; 2) .

12.8. Найдите пределы: 1) ; 2) ; 3) .

12.9. Найдите пределы: 1) ; 2) .

Домашнее задание 12.

12.10. Найдите пределы: 1) 2) 3) 4) ; 5) .

12.11. Найдите пределы: 1)  2)  3)  4)  5)  6) ; 7) ; 8) .

Занятие 13. Непрерывность. Точки разрыва.

Задачи

13.1. Запишите с помощью неравенств следующие утверждения: 1) ; 2) ; 3) ; 4) ; 5) ; 6) ; 7) ; 8) ; 9) ; 10) ; 11) .

13.2. 1) Дайте определение непрерывности функции в точке по Коши. 2) Пусть функция определена в некоторой окрестности точки. Сформулируйте в положительном смысле утверждение, что не является непрерывной в точке . 13.3. Пользуясь определением Коши, докажите непрерывность функции в каждой точке .

13.4. Исследуйте на непрерывность и постройте графики функций: 1) ; 2) .

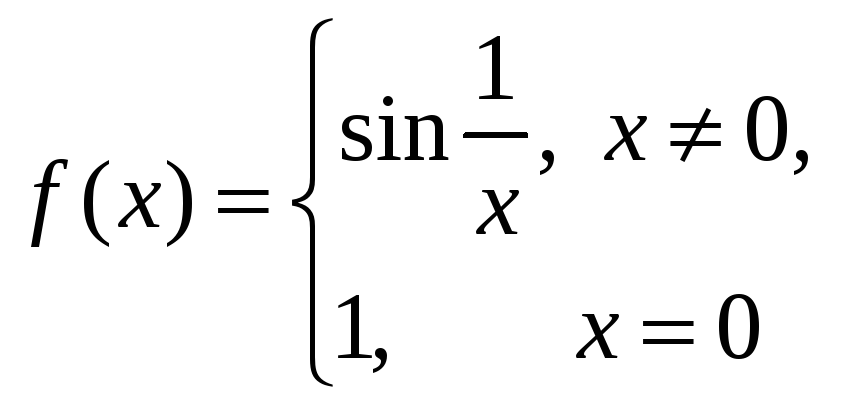13.5. Определите тип точек разрыва функций , если: 1) ; 2) ; 3) .

13.6. Пусть функция непрерывна в точке и . Найдите .

13.7. Исследуйте на непрерывность функцию .

13.8. При каком значении функция является непрерывной?

13.9. Исследуйте на непрерывность и постройте графики функций: 1) ; 2) .

13.10. Сформулируйте теорему о промежуточном значении непрерывной функции. Пусть функции и непрерывны на отрезке и , а . Докажите, что существует точка такая, что .

13.11. Докажите, что многочлен : а) имеет корень на отрезке ; б) имеет не менее трёх действительных корней.