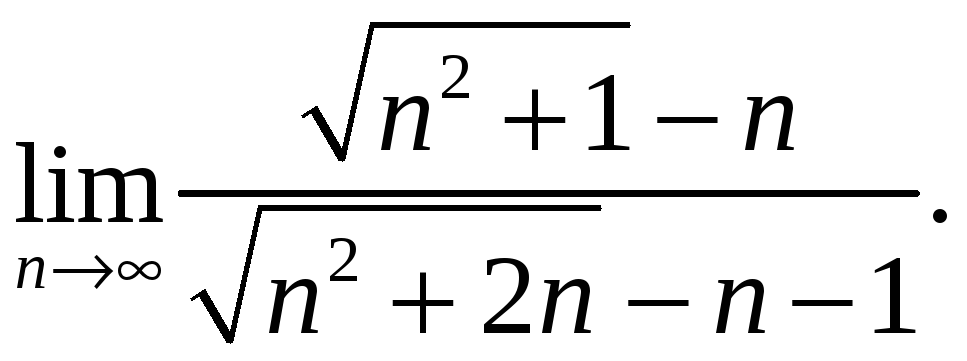- •Пример. Вычислить сумму .
- •Домашнее задание 1.
- •Занятие 2. Метод математической индукции.
- •Пример 1. Доказать, что сумма первых n нечётных чисел () равна .
- •Пример 2. Найти все натуральные числа n, для которых верно неравенство
- •Задачи.
- •Домашнее задание 2.
- •Занятие 3. Элементы комбинаторики. Формула бинома Ньютона.
- •Пример . Сколько шестизначных чисел, кратных 5, можно составить из цифр 1, 2, 3, 4, 5, 6 при условии, что в числе цифры не повторяются?
- •Задачи.
- •Домашнее задание 3.
- •Занятие 4. Действительные и комплексные числа.
- •Задачи.
- •Домашнее задание 4.
- •Занятие 5.Тригонометрическая форма комплексного числа.
- •Задачи.
- •Домашнее задание 5.
- •Занятие 6. Многочлены и рациональные дроби.
- •Пример 1. Решить уравнение .
- •Пример 2. Решить уравнение .
- •Пример 3. Записать многочлен в виде произведения двух многочленов второй степени с действительными коэффициентами.
- •►1) По формуле (3) представим: .
- •Задачи.
- •Домашнее задание 6.
- •Занятие 7. Функции и последовательности. Задачи
- •Домашнее задание 7.
- •Занятие 8. Предел последовательности. Задачи
- •Домашнее задание 8.
- •Занятие 9. Доказательство пределов. Задачи
- •Домашнее задание 9.
- •Занятие 10. Контрольная работа №1. Самоподготовка.
- •Занятие 11. Предел функции. Задачи
- •Домашнее задание 13.
- •Занятие 14. Сравнение функций. Вычисление пределов. Задачи
- •Домашнее задание 14.
- •Занятие 15. Производная, дифференциал, геометрический смысл. Задачи
- •Домашнее задание 15.
- •Занятие 16. Дифференцирование композиции. Задачи
- •Домашнее задание 16.
- •Домашнее задание 18.
- •Занятие 21. Неопределённый интеграл.
- •Домашнее задание 21.
- •Домашнее задание 28.
- •Занятие 29. Длина кривой. Объём тела вращения. Задачи
- •Домашнее задание 30.
- •Занятие 31. Контрольная работа №3. Самоподготовка.
Домашнее задание 6.
6.12.
При
делении
многочлена
![]() на
на
![]() получается
остаток
7, а при
делении
на
получается
остаток
7, а при
делении
на
![]() – остаток
3. Найдите
остаток
от
деления
– остаток
3. Найдите
остаток
от
деления
![]() на
на
![]() .
.
6.13.
Убедитесь в том,
что
число
![]() является
решением
уравнения
является
решением
уравнения
![]() и
найдите
остальные
решения.
и
найдите
остальные
решения.
6.14.
Определите
кратность
корня
![]() уравнения
уравнения
![]() .
.
6.15.
Представьте
многочлен
![]() в
виде
произведения
двух многочленов
второй
степени
с
действительными
коэффициентами.
в
виде
произведения
двух многочленов
второй
степени
с
действительными
коэффициентами.
6.16.
Разложите
правильную
рациональную
функцию
на сумму
простых дробей:
1) 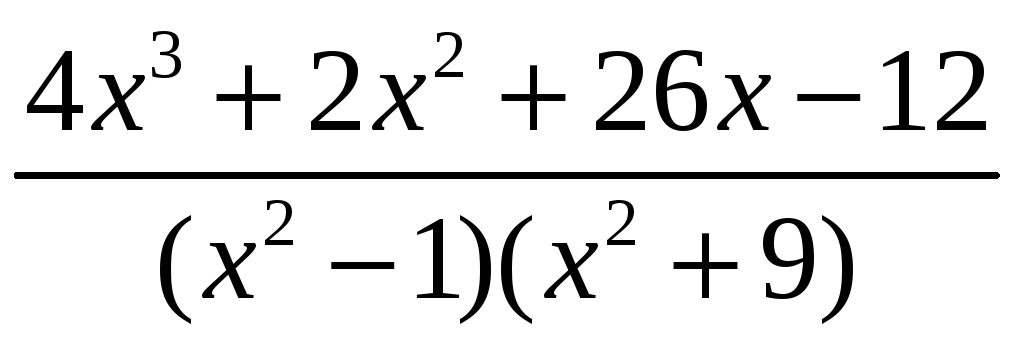 ;
2)
;
2) 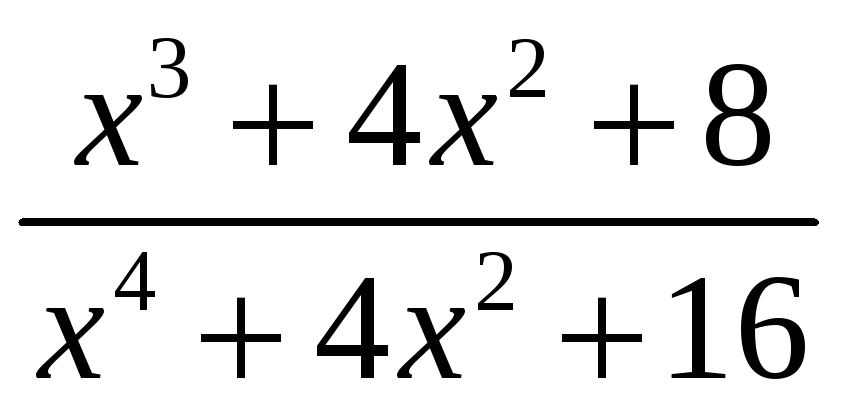 .
.
Занятие 7. Функции и последовательности. Задачи
7.1.
Для функции f(x)
=
![]() найдите f(0),
найдите f(0),
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
7.2.
Найдите
![]() ,
если: 1)
,
если: 1)
![]() ;
2)
;
2)
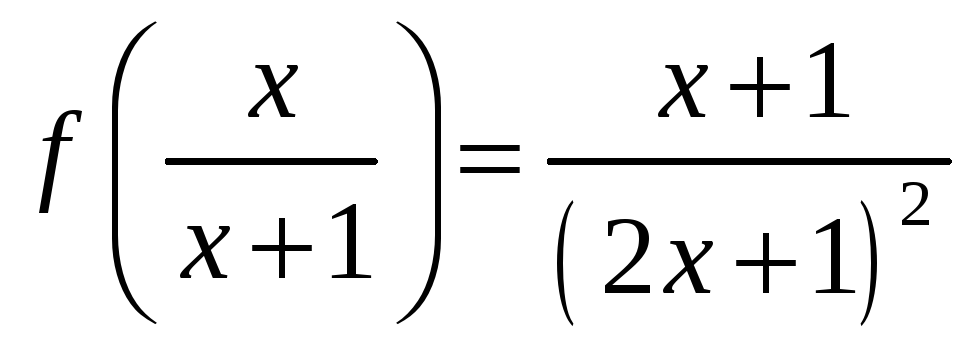 .
.
7.3.
Пусть
![]() ,
,
![]() ,
,
![]() .
Запишите формулы, задающие композиции:
1)
f
.
Запишите формулы, задающие композиции:
1)
f![]() g;
2)
g
g;
2)
g![]() f;
3) f
f;
3) f![]() φ
φ![]() g;
4) g
g;
4) g![]() φ
φ![]() f
;
5) φ
f
;
5) φ![]() g
g![]() f
.
f
.
7.4.
Постройте графики функций:
1)
y
=
![]() ;
2)
y=
;
2)
y=![]() ;
3)
y=
;
3)
y=![]() ;
4)
y=sgn(x
;
4)
y=sgn(x![]() –4).
–4).
7.5.
Пусть
![]() =
2x
– 1.
Постройте графики функций:
=
2x
– 1.
Постройте графики функций:
![]() ;
;
![]() –
–![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
7.6.
Запишите
5 первых
членов
последовательности,
заданной
формулой
общего
члена:
1) ![]()
![]() ;
2)
;
2) 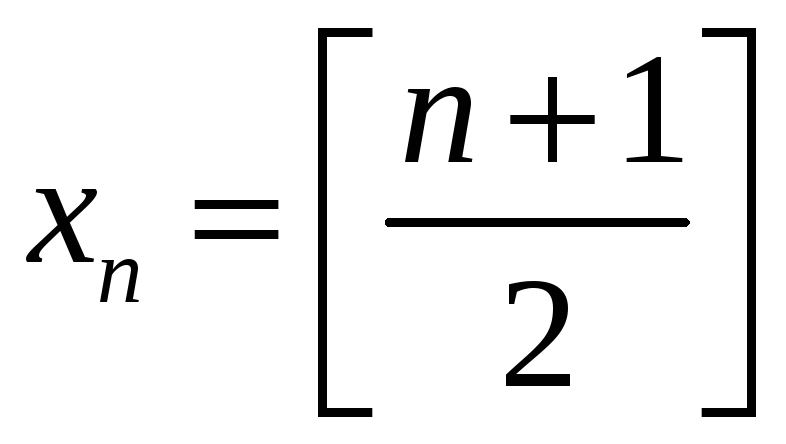 ;
3)
;
3) ![]() ;
4)
;
4)
![]() ;
5)
;
5) ![]() ;
6)
;
6) 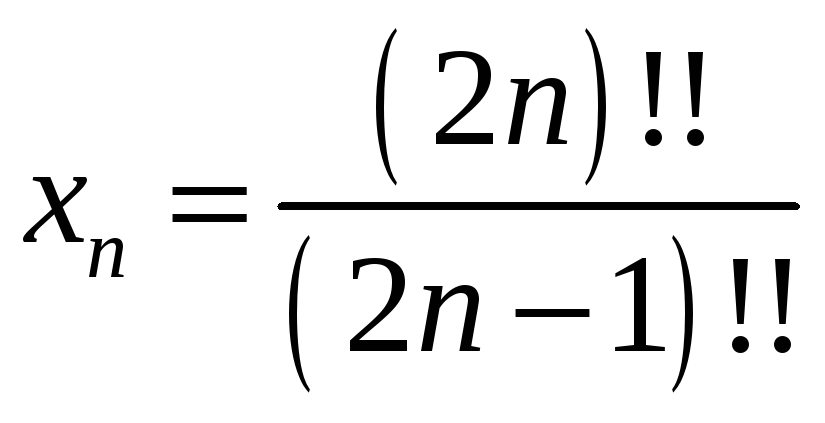 ,
где
,
где
![]() ,
,
![]() .
.
7.7.
Запишите 5 первых членов последовательности,
заданной рекуррентной
формулой:
![]() ,
,
![]() .
.
7.8.
Являются ли ограниченными последовательности:
1) ![]() ;
2)
;
2) ![]() ;
3)
;
3)  ?
?
Домашнее задание 7.
7.9.
Постройте графики функций:
1) y
=
![]() ;
2) y
= x
+
;
2) y
= x
+
![]() ;
3) y
= sgn(sinx);
4) y
= cosx
+
;
3) y
= sgn(sinx);
4) y
= cosx
+
![]() .
.
7.10. Найдите формулу общего члена последовательности, у которой члены с чётными номерами равны 1, а члены с нечётными номерами равны 0.
7.11.
Докажите,
что
следующие
последовательности
ограничены:
1) ![]() ;
2)
;
2) ![]() .
.
7.12.
Найдите
точные
верхнюю и
нижнюю
границы
последовательности
![]() .
.
Занятие 8. Предел последовательности. Задачи
8.1.
Пользуясь
определением
предела
последовательности,
докажите,
что
![]()
8.2.
Докажите,
что
следующие
последовательности
являются
бесконечно
малыми![]() 1)
1) ![]() (
(![]() );
2)
);
2) ![]() .
.
8.3.
Докажите, что: 1)
![]() ;
2)
;
2) ![]() если
если
![]() .
.
8.4.
Найдите
предел
последовательности:
1) 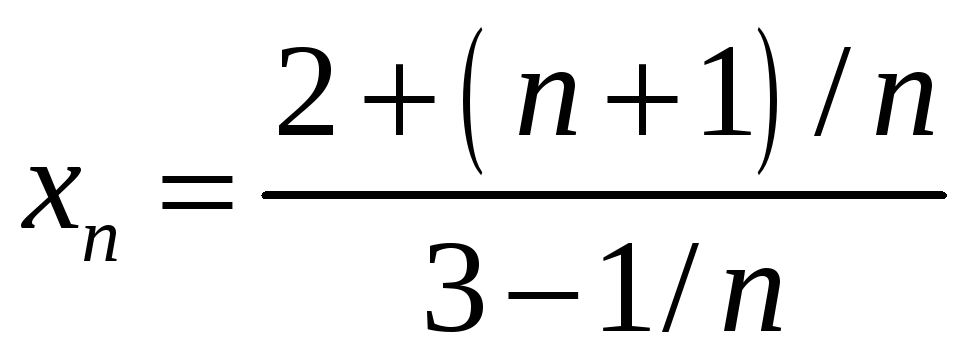 ;
2)
;
2) 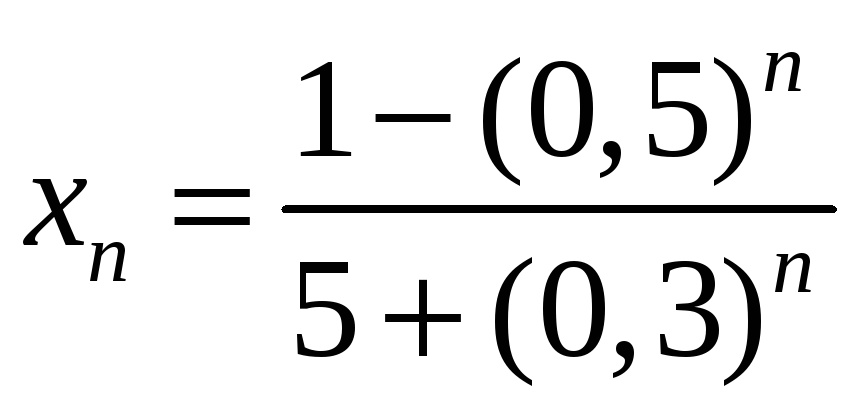 ;
3)
;
3) 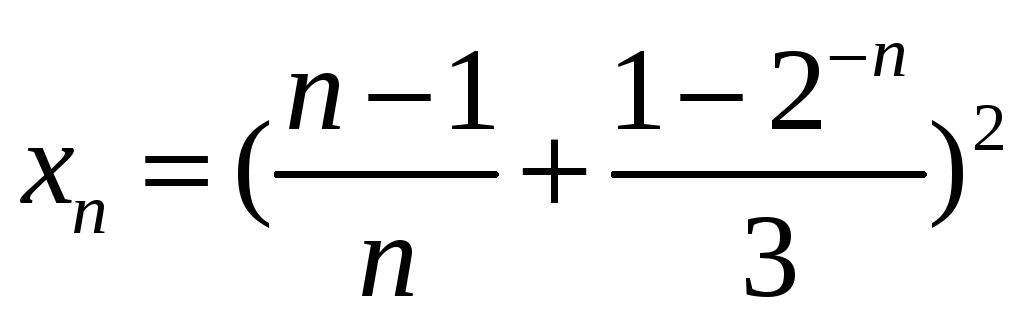 ;
4)
;
4) 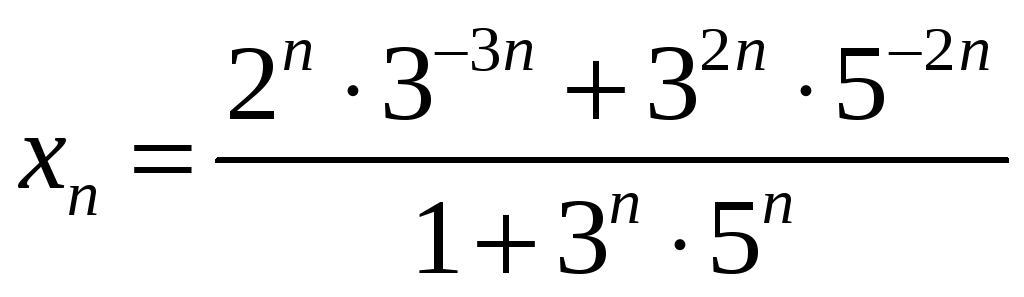 .
.
8.5.
Раскройте
неопределённость
![]() (т.е.
найдите
предел
последовательности
(т.е.
найдите
предел
последовательности
![]() )
путём
предварительного
деления
числителя
и
знаменателя
дроби
на
соответствующую
степень
)
путём
предварительного
деления
числителя
и
знаменателя
дроби
на
соответствующую
степень
![]() или
или
![]() :
1)
:
1) ![]() ;
2)
;
2) 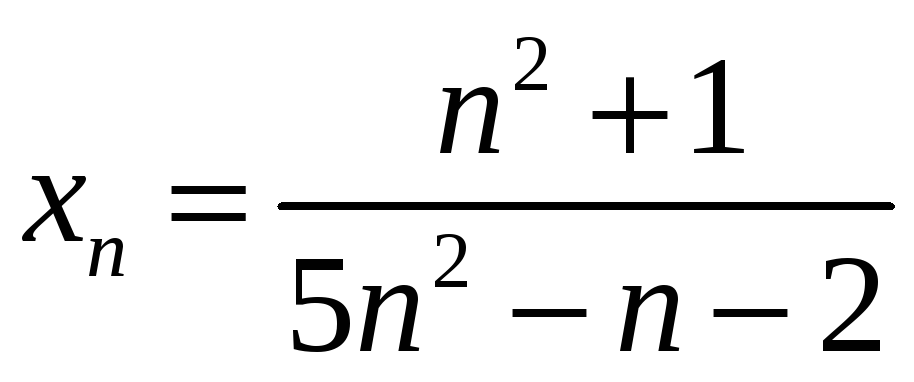 ;
3)
;
3) 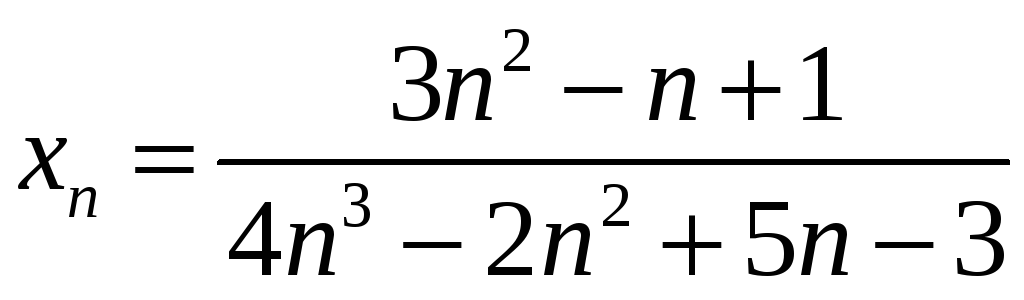 ;
4)
;
4) 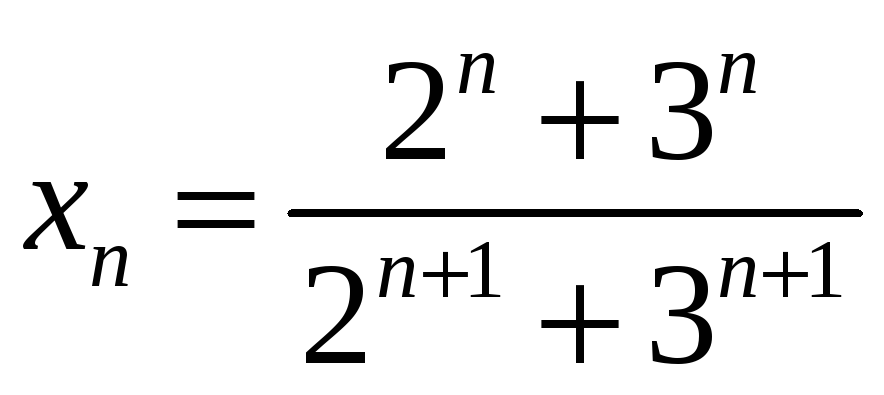 ;
5)
;
5) ![]() ;
6)
;
6)![]()
8.6.
Найдите
пределы
следующих
иррациональных
выражений,
используя
приём
переведения
иррациональности
из
знаменателя
в
числитель
или
из
числителя
в
знаменатель:
1) ![]() ;
2)
;
2) ![]() ;
3)
;
3) ![]() .
.
Домашнее задание 8.
8.7.
Пользуясь
определением
предела
последовательности,
докажите,
что
![]()
8.8.
Раскройте
неопределённость
![]() (т.е.
найдите
предел
последовательности
(т.е.
найдите
предел
последовательности
![]() )
путём
предварительного
деления
числителя
и
знаменателя
дроби
на
соответствующую
степень
)
путём
предварительного
деления
числителя
и
знаменателя
дроби
на
соответствующую
степень
![]() или
или
![]() :
1)
:
1)  ;
2)
;
2) ![]() ;
3)
;
3) 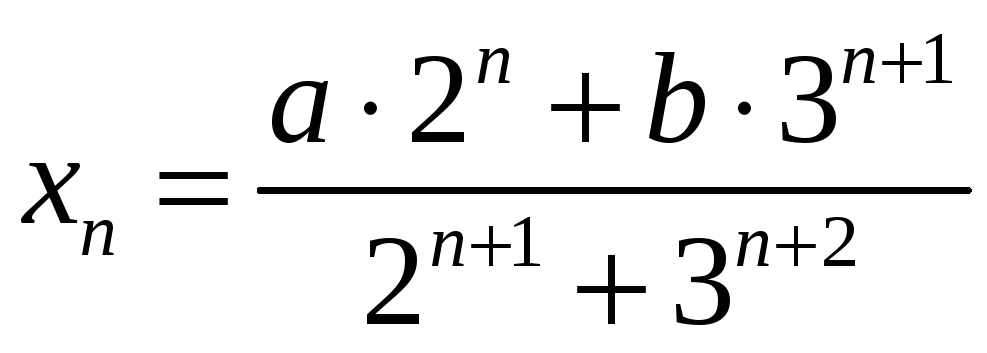 ;
4)
;
4) ![]() .
.
8.9. Докажите,
что
последовательность
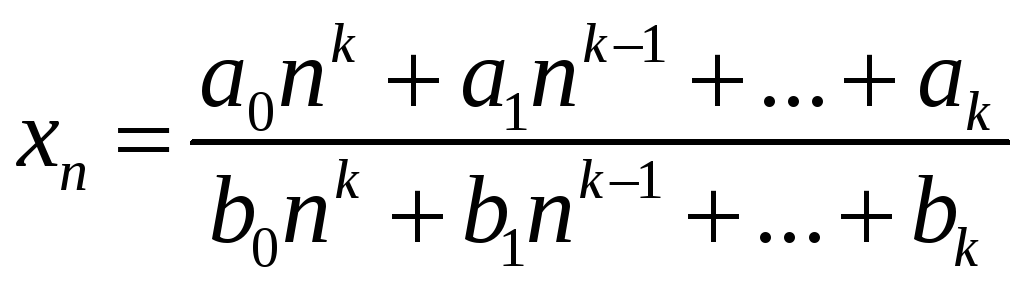 сходится
к
пределу
сходится
к
пределу
![]() ,
если
,
если
![]() .
.
8.10.
Найдите
пределы
следующих
иррациональных
выражений,
используя
приём
переведения
иррациональности
из
знаменателя
в
числитель
или
из
числителя
в
знаменатель:
1) ![]() ;
2)
;
2)