Домашнее задание 3.

3.14. На книжной полке стоит собрание произведений в 10 томах. Сколькими способами можно разместить эти книги, чтобы: 1) тома 1 и 2 стояли рядом; 2) тома 3 и 4 не стояли рядом?

3.15. В колоде 36 карт, из которых 4 туза. Сколькими способами можно раздать 6 карт, чтобы: 1) среди них не было тузов; 2) среди них было два туза; 3) среди них был хатя бы один туз?

3.16. На одной из двух параллельных прямых лежат 11 точек, на другой – 13. Сколько существует треугольников с вершинами в этих точках?

3.17. Сколько делителей имеет число 210?

3.18. Найти член разложения по формуле бинома Ньютона выражения 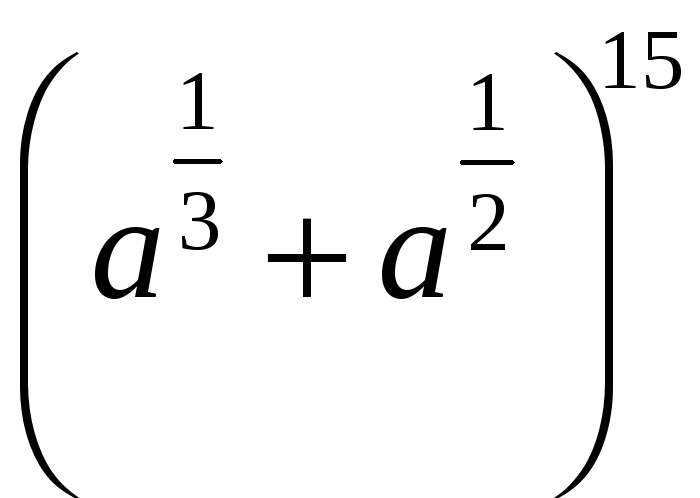, не зависящий от .

3.19. Найдите сумму коэффициентов разложения бинома при каждом натуральном n.

3.20. Найдите коэффициент многочлена (1 + x² – x³)⁹ при x⁸.

3.21.Найдите слагаемые разложения бинома , являющиеся целыми числами.

Занятие 4. Действительные и комплексные числа.

1º. Бесконечная десятичная дробь называется действительным числом. Множество действительных чисел обозначается . Числа , где , называются рациональными, а само выражение – рациональной дробью. Множество всех рациональных чисел обозначается . Каждое рациональное число можно записать в виде десятичной дроби. Бесконечные десятичные периодические дроби и только они являются рациональными числами. Действительное число, не являющееся рациональным, называется иррациональным.

2º. Пусть X есть подмножество множества действительных чисел, . Множество X называется ограниченным сверху (снизу), если существует такое действительное число , что для всех выполняется неравенство ; число A (a) называется верхней границей (нижней границей) множества Х. Множество, ограниченае сверху и снизу, называется ограниченным. Наименьшая (наибольшая) из всех верхних (нижних) границ множества называется точной верхней (нижней) границей множества X и обозначается (). Если множество не ограничено сверху (снизу), то считают .Если M = (m = ), то: 1)  ; 2)  : . Если m и M являются конечными числами, то условия 2) равносильны условиям  : ().

Теорема о гранях. Каждое ограниченнае сверху (снизу) непустое множество действительных чисел имеет конечную точную верхнюю (нижнюю) границу.

3º. Алгебраической формой комплексного числа z называется выражение , где x, y – действительные числа, i – мнимая единица. Действительные числа x и y называются соответственно действительной и мнимой частями числа z и обозначаются x = Re z, y = Im z. Два комплексные числа и называются равными, если и тольки если . Комплексное число x – iy называется сопряжённым комплексному числоу x + iу и обозначается .

Арифметические действия над комплексными числами и выполняются по правилам: 1) ; 2) ; 3) ; 4) .

Геометрически каждому комплексному числу соответствует точка М(x;y) координатной плоскасти и, наоборот, каждой точке М(x; y) плоскости соответствует комплексное число . Эту плоскость называют комплексной плоскастью, ось абсцисс – действительной осью, а ось ординат – мнимой осью. Иногда бывает более удобно представлять комплексное число как вектор с началом в точке О и концом в точке M.

Пример. Превратить бесконечную десятичные периодические дроби a = 3,(17) и b = 2,5(123) в обыкновенную дробь.

▶ 1) Умножим число a на 100 и получим 100а = 317,(17). Если от обеих частей этого равенства вычесть число а, то получим 99а = 314, откуда а = 314/99.

2) Если обозначить x = 10b = 25,(123), то, как и в предыдущем случае, число x превращается в обыкновенную дробь: 1000х = 25123,(123); 999x = 25098, x = 25098/999, а затем b = 25098/9990 ◄