
- •Пример. Вычислить сумму .
- •Домашнее задание 1.
- •Занятие 2. Метод математической индукции.
- •Пример 1. Доказать, что сумма первых n нечётных чисел () равна .
- •Пример 2. Найти все натуральные числа n, для которых верно неравенство
- •Задачи.
- •Домашнее задание 2.
- •Занятие 3. Элементы комбинаторики. Формула бинома Ньютона.
- •Пример . Сколько шестизначных чисел, кратных 5, можно составить из цифр 1, 2, 3, 4, 5, 6 при условии, что в числе цифры не повторяются?
- •Задачи.
- •Домашнее задание 3.
- •Занятие 4. Действительные и комплексные числа.
- •Задачи.
- •Домашнее задание 4.
- •Занятие 5.Тригонометрическая форма комплексного числа.
- •Задачи.
- •Домашнее задание 5.
- •Занятие 6. Многочлены и рациональные дроби.
- •Пример 1. Решить уравнение .
- •Пример 2. Решить уравнение .
- •Пример 3. Записать многочлен в виде произведения двух многочленов второй степени с действительными коэффициентами.
- •►1) По формуле (3) представим: .
- •Задачи.
- •Домашнее задание 6.
- •Занятие 7. Функции и последовательности. Задачи
- •Домашнее задание 7.
- •Занятие 8. Предел последовательности. Задачи
- •Домашнее задание 8.
- •Занятие 9. Доказательство пределов. Задачи
- •Домашнее задание 9.
- •Занятие 10. Контрольная работа №1. Самоподготовка.
- •Занятие 11. Предел функции. Задачи
- •Домашнее задание 13.
- •Занятие 14. Сравнение функций. Вычисление пределов. Задачи
- •Домашнее задание 14.
- •Занятие 15. Производная, дифференциал, геометрический смысл. Задачи
- •Домашнее задание 15.
- •Занятие 16. Дифференцирование композиции. Задачи
- •Домашнее задание 16.
- •Домашнее задание 18.
- •Занятие 21. Неопределённый интеграл.
- •Домашнее задание 21.
- •Домашнее задание 28.
- •Занятие 29. Длина кривой. Объём тела вращения. Задачи
- •Домашнее задание 30.
- •Занятие 31. Контрольная работа №3. Самоподготовка.
Занятие 21. Неопределённый интеграл.
ТАБЛИЦА НЕОПРЕДЕЛЁННЫХ ИІНТЕГРАЛОВ
1.
![]() 2.
2.![]()
3.
![]() ;
4.
;
4.![]()
5.![]() 6.
6.![]()
7.![]() 8.
8.![]()
9.![]() 10.
10.
11. 12.
12.

13.![]() 14.
14.![]()
15.![]() 16.
16.![]()
Задачи
21.1.
 .
21.2.
.
21.2.
 .
21.3.
.
21.3.
 .
21.4.
.
21.4.
 .
.
21.5.
![]() .
21.6.
.
21.6.
![]() .
21.7.
.
21.7.
 .
21.8.
.
21.8.
![]() .
.
21.9.
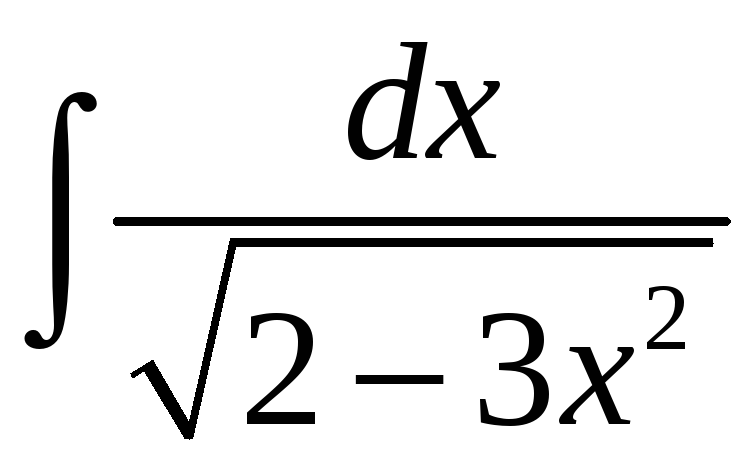 .
21.10.
.
21.10.
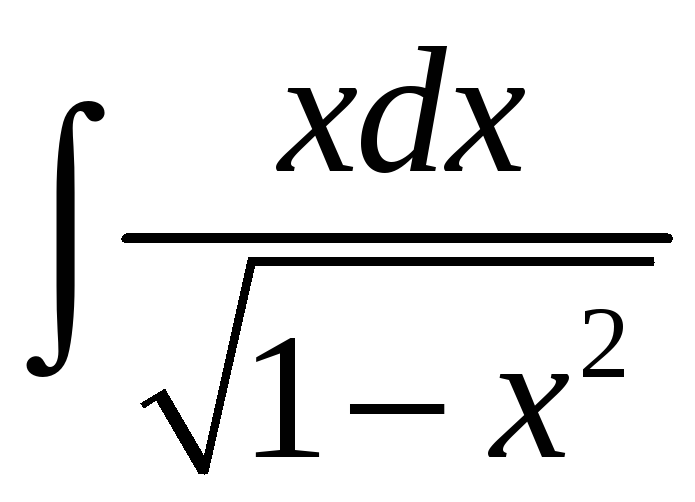 .
21.11.
.
21.11.
![]() .
21.12.
.
21.12.
 .
.
21.13.
![]() .
21.14.
.
21.14.
![]() .
21.15.
.
21.15.
 .
21.16.
.
21.16.
 .
.
21.17.
![]() .
21.18.
.
21.18.
 .
21.19.
.
21.19.
 .
.
Домашнее задание 21.
21.20.
Найдите функцию
![]() ,
которая имеет производную
,
которая имеет производную
![]() и при
и при
![]() принимает значение 5.
принимает значение 5.
21.21.
Пользуясь определением неопределённого
интеграла, проверьте следующее
равенство
![]()
![]() .
.
21.22.
Путём
тождественных
преобразований
подынтегральной
функции
найдите
интегралы:
1)
 ;
2)
;
2) ![]() ;
3)
;
3) ![]() ;
4)
;
4)  ;
;
5) 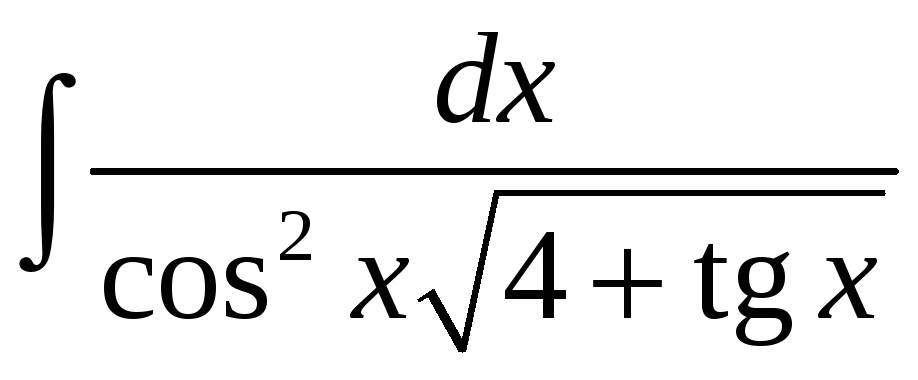 ;
6)
;
6)  ;
7)
;
7)  ;
8)
;
8)  ;
9)
;
9)  ;
10)
;
10)  ;
11)
;
11) ![]() (подсказка:
(подсказка:
![]() );
12)
);
12)  (подсказка:
(подсказка:
![]() ).
).
21.23.
Найдите
интегралы:
1) ![]() ;
2)
;
2)  ;
3)
;
3) ![]() ;
4)
;
4)  ;
;
5) ![]() ;
6)
;
6) 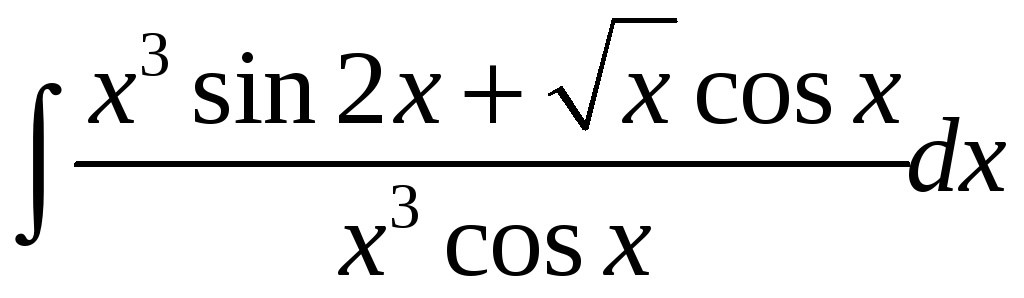 ;
7)
;
7)  ;
;
8) ![]() ;
9)
;
9)
 ;
10)
;
10) 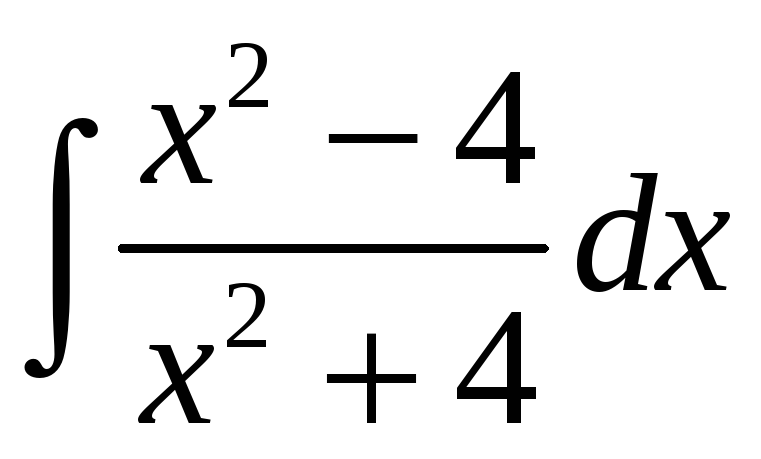 ;
11)
;
11)  ;
;
12)  ;
13)
;
13)  ;
14)
;
14)  .
.
Занятие 22. Интегрирование по частям.
Задачи
Найдите интегралы методом интегрирования по частям:
22.1.
![]() .
22.2.
.
22.2.
![]() .
22.3.
.
22.3.
![]() .
22.4.
.
22.4.
![]() .
.
22.5.
![]() .
22.6.
.
22.6.
![]() .
22.7.
.
22.7.
![]() .
22.8.
.
22.8.
![]() .
.
22.9.
![]() .
22.10.
.
22.10.
![]() .
.
Домашнее задание 22.
22.11.
![]() .
22.12.
.
22.12.
 .
22.13.
.
22.13.
![]() .
.
22.14.
![]() 22.15.
22.15.
![]() .
22.16.
.
22.16.
![]() .
.
Занятие 23. Интегрирование рациональных функций.
Задачи
23.1.
![]() .
23.2.
.
23.2.
 .
23.3.
.
23.3.
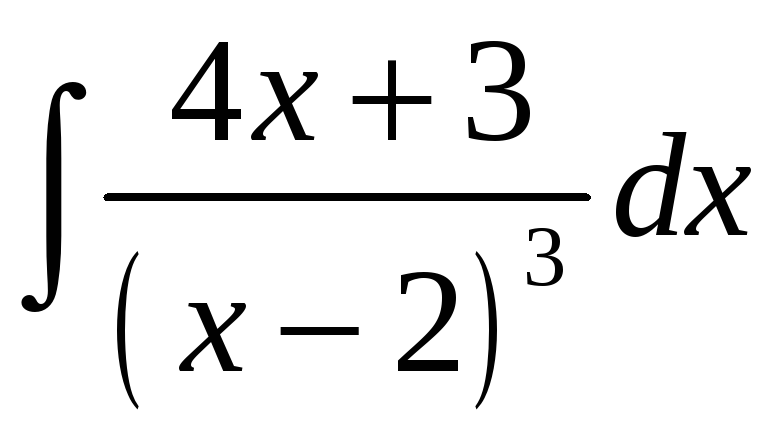 .
.
23.4.
![]() .
23.5.
.
23.5.
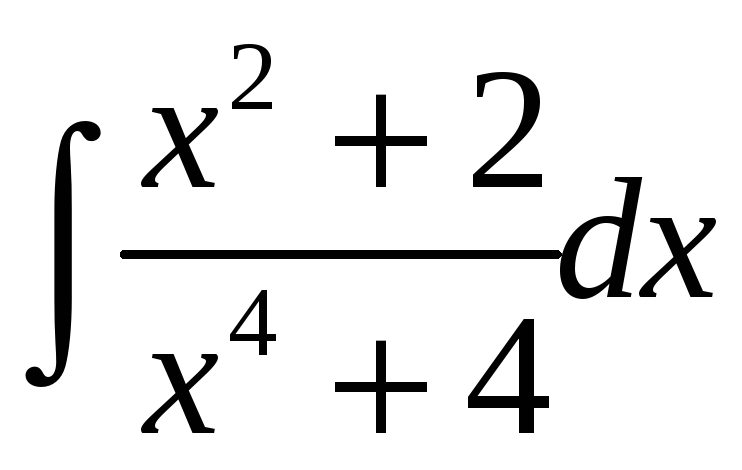 .
23.6.
.
23.6.
 .
.
23.7.
![]() .
23.8.
.
23.8.
 .
.
Домашнее задание 23.
23.9.
 .
23.10.
.
23.10.
 .
23.11.
.
23.11.
![]() .
.
23.12.
 .
23.13.
.
23.13.
 .
23.14.
.
23.14.
 .
.
Занятие 24.
Интегрирование дробно-линейных иррациональностей. Подстановки Чебышёва.
Задачи
24.1.
 24.2.
24.2.
 24.3.
24.3.

24.4.
 .
24.5.
.
24.5.
 .
24.6.
.
24.6.
![]() .
.
Домашнее задание 24.
24.7.
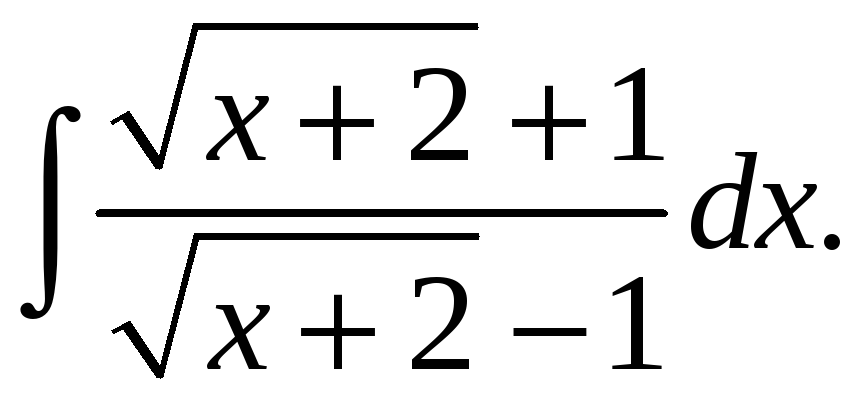 24.8.
24.8.
 24.9.
24.9.
 .
.
24.10.
![]() .
24.11.
.
24.11.
 .
.
Занятие 25.
Интегрирование рационально-тригонометрических функций.
Задачи
25.1.
![]() .
25.2.
.
25.2.
![]() .
25.3.
.
25.3.
![]() .
.
25.4.
 .
25.5.
.
25.5.
![]() .
25.6.
.
25.6.
![]() .
.
25.7.
![]() .
25.8.
.
25.8.
![]() .
25.9.
.
25.9.
![]() .
.
Домашнее задание 25.
25.10.
![]() .
25.11.
.
25.11.
 .
25.12.
.
25.12.
![]() .
.
25.13.
![]() .
25.14.
.
25.14.
![]() .
25.15.
.
25.15.
 .
25.16.
.
25.16.
![]() .
.
Занятие 26.
Интегрирование квадратичных иррациональностей.
Задачи
26.1.
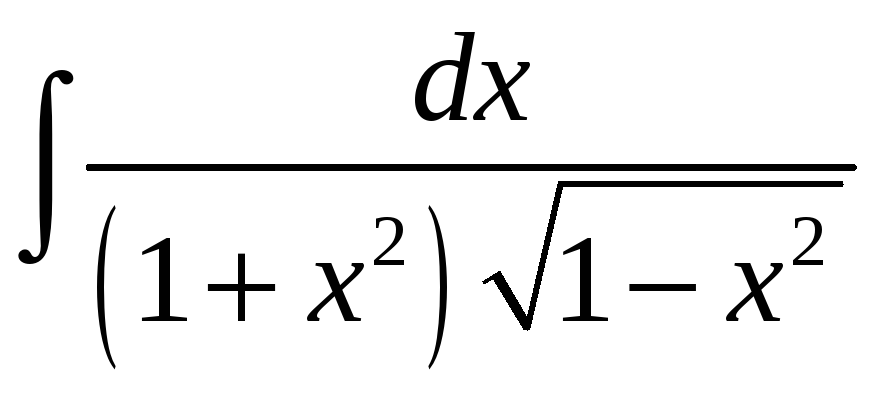 .
26.2.
.
26.2.
![]() .
26.3.
.
26.3.
 .
.
26.4.
 .
26.5.
.
26.5.
 .
.
Домашнее задание 26.
26.6.
 .
26.7.
.
26.7.
 .
.
26.8.
 .
26.9.
.
26.9.
 .
.
Занятие 27.
Определённый интеграл.
Задачи
27.1.
Найдите интегральную сумму
![]() и вычислите интеграл для функции
и вычислите интеграл для функции
![]() на отрезке
на отрезке
![]() ,
разделяя его на
,
разделяя его на
![]() равных отрезков и выбирая
значения
равных отрезков и выбирая
значения
![]() в серединах этих отрезков.
в серединах этих отрезков.
27.2.
Для функции
![]() найдите суммы Дарбу
найдите суммы Дарбу
![]() и
и
![]() на отрезке
на отрезке
![]() ,
разделив его на
,
разделив его на
![]() равных отрезков.
равных отрезков.
27.3.
Какой из интегралов больше:
1)
 или
или
 ;
2)
;
2)
 или
или
 ?
?
27.4.
Вычислить:
1)
 .
2)
.
2)
 .
.
27.5.
Пользуясь формулой Ньютона-Лейбница,
вычислить
 .
.
27.6. Почему формальное использование формулы Ньютона-Лейбница приводит к неправильному результату:
1)
![]() ;
2)
;
2)
 ;
3)
;
3)
 ?
?
27.7.
Вычислите интеграл
 .
.
27.8.
Вычислить: 1)
 ;
2)
;
2)
 ;
3)
;
3)
 .
.
27.9.
Вычислить:
1)
 ;
2)
;
2)
 ;
3)
;
3)
 .
.
27.10.
Вычислить
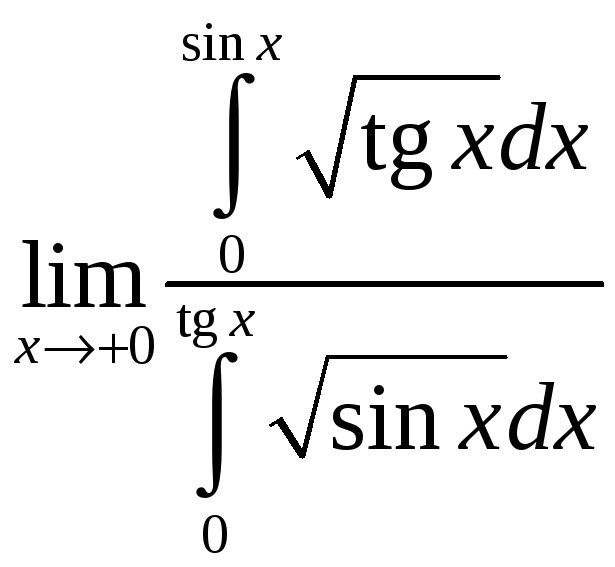 .
.
Домашнее задание 27.
27.11.
Вычислить
 .
.
27.12.
Вычислить: 1)
 ;
2)
;
2)
 .
.
27.13.
Вычислить
 .
.
27.14.
Найти
 ,
если
,
если

Занятие 28.
Замена переменных. Интегрирование по частям.
Вычисление площадей
Задачи
27.1.
Применяя формулу интегрирования по
частям, вычислить:
1)
 ;
2)
;
2)
 .
.
27.2.
Применяя подходящую замену переменной,
вычислите интегралы:
1)
 ;
2)
;
2)
 .
.
27.3.
Доказать, что если
![]() непрерывна на
непрерывна на
![]() ,
то
,
то
 .
.
27.4.
Получив рекуррентную формулу, вычислите
интегралы:
1)
 ;
2)
;
2)

27.5.
Найдите площади фигур, ограниченных
кривыми, заданными в прямоугольных
координатах: 1)
![]() .
2)
.
2)
![]() .
.
27.6.
Найдите площади фигур, ограниченных
кривыми, заданными в полярных
координатах:
1)
![]() (кардиоида);
(кардиоида);
2)
![]() (точка
(точка
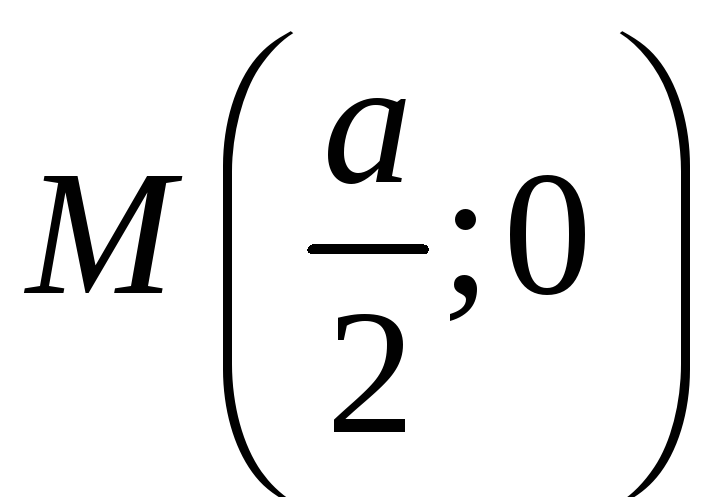 принадлежит фигуре.
принадлежит фигуре.
