
- •Пример. Вычислить сумму .
- •Домашнее задание 1.
- •Занятие 2. Метод математической индукции.
- •Пример 1. Доказать, что сумма первых n нечётных чисел () равна .
- •Пример 2. Найти все натуральные числа n, для которых верно неравенство
- •Задачи.
- •Домашнее задание 2.
- •Занятие 3. Элементы комбинаторики. Формула бинома Ньютона.
- •Пример . Сколько шестизначных чисел, кратных 5, можно составить из цифр 1, 2, 3, 4, 5, 6 при условии, что в числе цифры не повторяются?
- •Задачи.
- •Домашнее задание 3.
- •Занятие 4. Действительные и комплексные числа.
- •Задачи.
- •Домашнее задание 4.
- •Занятие 5.Тригонометрическая форма комплексного числа.
- •Задачи.
- •Домашнее задание 5.
- •Занятие 6. Многочлены и рациональные дроби.
- •Пример 1. Решить уравнение .
- •Пример 2. Решить уравнение .
- •Пример 3. Записать многочлен в виде произведения двух многочленов второй степени с действительными коэффициентами.
- •►1) По формуле (3) представим: .
- •Задачи.
- •Домашнее задание 6.
- •Занятие 7. Функции и последовательности. Задачи
- •Домашнее задание 7.
- •Занятие 8. Предел последовательности. Задачи
- •Домашнее задание 8.
- •Занятие 9. Доказательство пределов. Задачи
- •Домашнее задание 9.
- •Занятие 10. Контрольная работа №1. Самоподготовка.
- •Занятие 11. Предел функции. Задачи
- •Домашнее задание 13.
- •Занятие 14. Сравнение функций. Вычисление пределов. Задачи
- •Домашнее задание 14.
- •Занятие 15. Производная, дифференциал, геометрический смысл. Задачи
- •Домашнее задание 15.
- •Занятие 16. Дифференцирование композиции. Задачи
- •Домашнее задание 16.
- •Домашнее задание 18.
- •Занятие 21. Неопределённый интеграл.
- •Домашнее задание 21.
- •Домашнее задание 28.
- •Занятие 29. Длина кривой. Объём тела вращения. Задачи
- •Домашнее задание 30.
- •Занятие 31. Контрольная работа №3. Самоподготовка.
Занятие 16. Дифференцирование композиции. Задачи
16.1. Сделать на доске задание 15.11.
16.2.
Вычислить производные следующих
функций:
1)
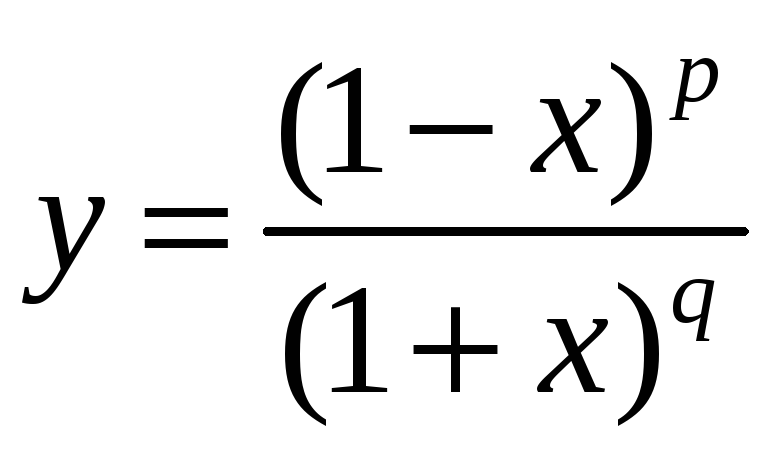 ;
2)
;
2)
![]() ;
3)
;
3)
![]() ;
4)
;
4)
![]() 5)
5)
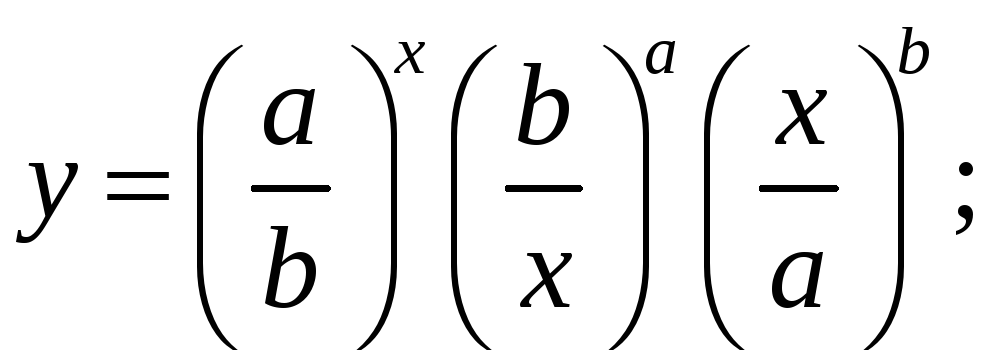 6)
6)
![]() ;
7)
;
7)
![]() ;
8)
;
8)
![]() ;
9)
;
9)
![]() ;
10)
;
10)
![]() ;
11)
;
11)
![]() ,
,
![]() ;
12)
;
12)
![]() ,
,![]() ,
,
![]() .
.
16.3.
Найдите
производную
функции
![]() в
точке
в
точке
![]() ,
если:
1)
,
если:
1) ![]() ,
, ![]() =0;
2)
=0;
2) 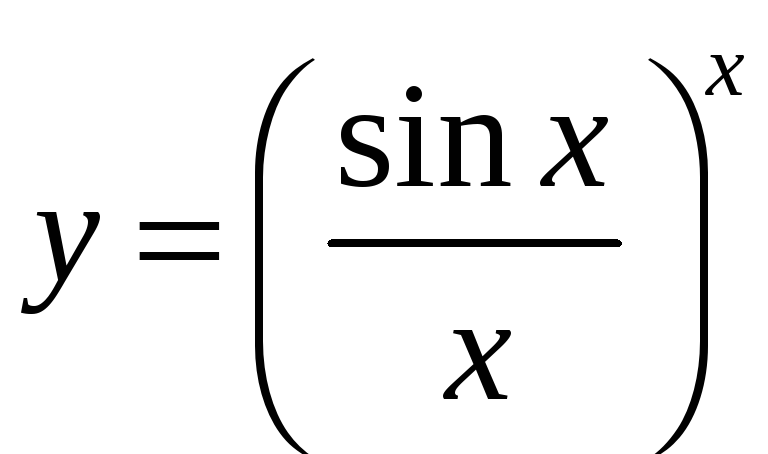 ,
,
![]() =
=![]() .
.
16.4.
Для функции
![]() вычислите
вычислите
![]() и
и
![]() .
.
16.5.
Исследуйте, является ли функция
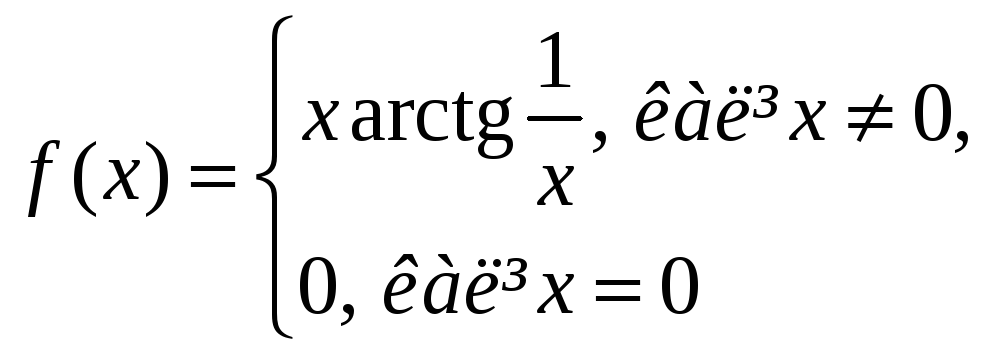 в точке
в точке
![]() :
а)
непрерывной;
б)
диффе
ренцируемой?
:
а)
непрерывной;
б)
диффе
ренцируемой?
16.6.
Определите,
при
каких
![]() и
и
![]() функция
функция
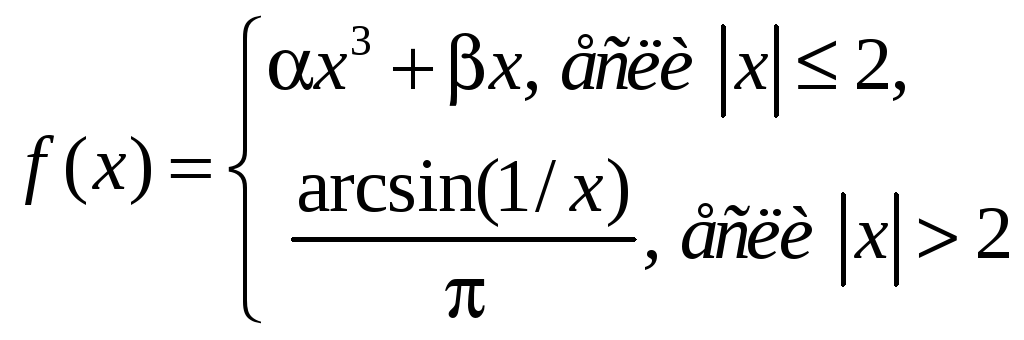 является:
а)
везде
непрерывной;
б)
везде
дифференцируемой.
Для
этих
значений
является:
а)
везде
непрерывной;
б)
везде
дифференцируемой.
Для
этих
значений
![]() и
и
![]() найдите
производные
этой фунции.
найдите
производные
этой фунции.
Домашнее задание 16.
16.7.
Вычислить производные следующих
функций:
1)
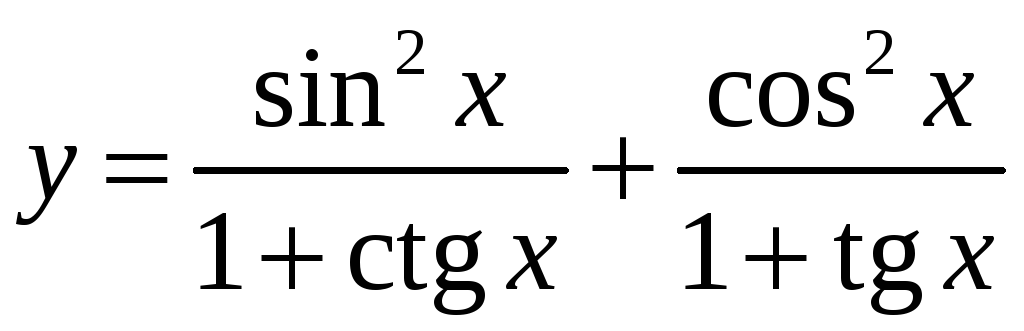 ;
2)
;
2)
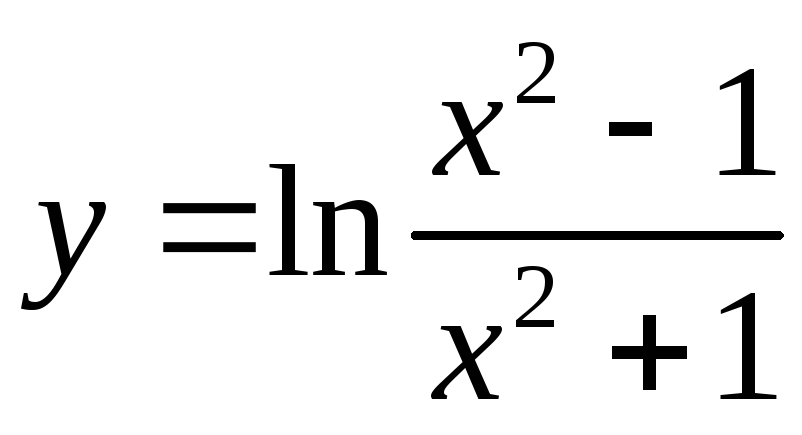 ;
3)
;
3)
![]() ;
4)
;
4)
![]() ;
5)
;
5)
![]() ;
;
6)
![]() ,
, ![]() ;
7)
;
7)
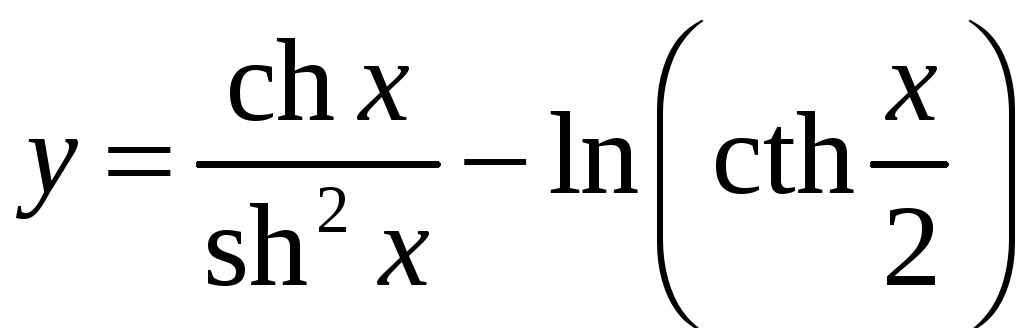 ;
;
8)
![]() ;
9)
;
9)
![]() ,
,
![]() .
.
16.8.
Найдите
производную
функции
![]() в
точке
в
точке
![]() .
.
16.9.
Для функции
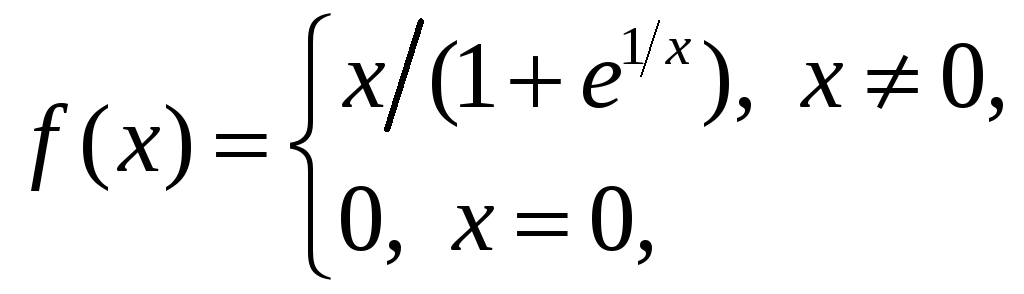 вычислите
вычислите
![]() и
и
![]() .
.
16.10.
Исследуйте, является ли функция
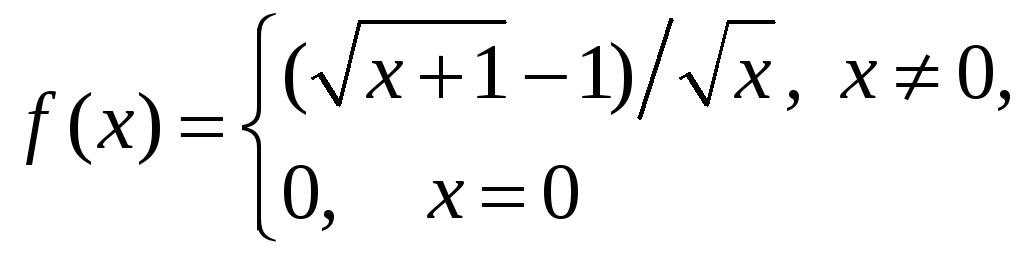 в точке
в точке
![]() :
а)
непрерывной;
б)
диффе
ренцируемой?
:
а)
непрерывной;
б)
диффе
ренцируемой?
16.11.
Определите,
при
каких
![]() и
и
![]() функция
функция
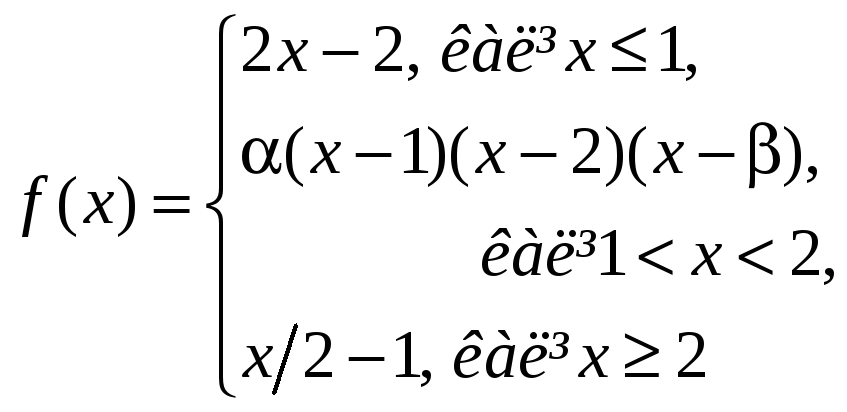 является:
а)
везде
непрерывной;
б)
везде
дифференцируемой.
Для
этих
значений
является:
а)
везде
непрерывной;
б)
везде
дифференцируемой.
Для
этих
значений
![]() и
и
![]() найдите
производные
этой фунции.
найдите
производные
этой фунции.
Занятие 17.
Дифференцирование обратных, неявных
и параметрических функций.
Задачи
17.1.
Найдите производную функции, обратной
к функции:
1)![]() ;
2)
;
2)
![]() в точке
в точке
![]() .
.
17.2.
Найдите производную
![]() функции, заданной неявно:
1)
функции, заданной неявно:
1)
![]() ;
2)
;
2)
![]() .
.
17.3.
Найдите производную
![]() функции, заданной параметрически:
1)
функции, заданной параметрически:
1)
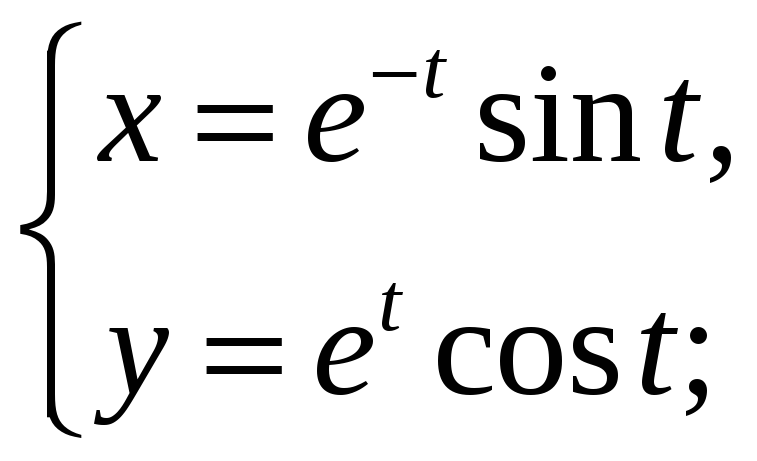 2)
2)
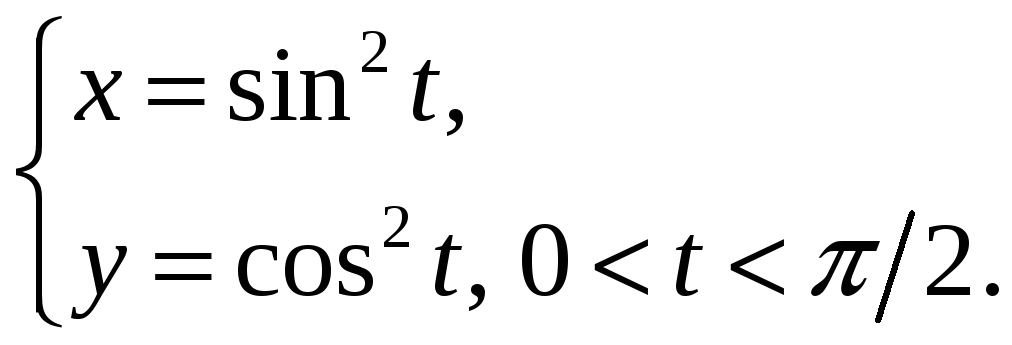
17.4.
Найдите в точке
![]() дифференциал функции
дифференциал функции
![]() ,
заданной
параметрически
,
заданной
параметрически
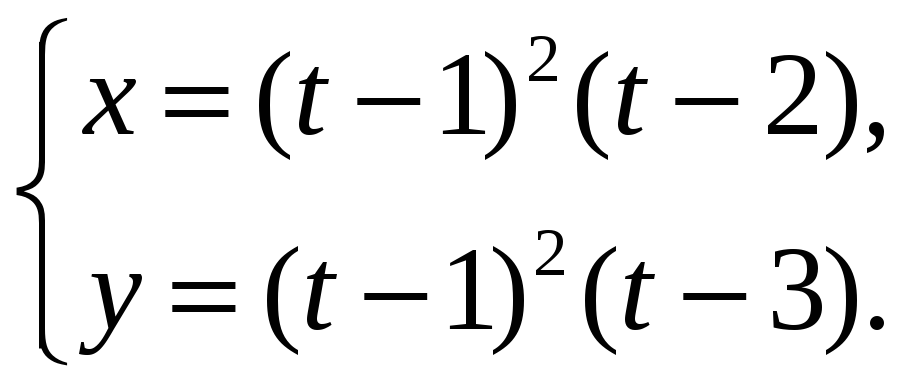
17.5.
Покажите, что функция
![]() ,
заданная неявно уравнением
,
заданная неявно уравнением
![]() ,
удовлетворяет уравнению
,
удовлетворяет уравнению
![]() .
.
17.6.
Найдите
![]() для функции
для функции
![]() ,
заданной
в
полярных
координатах
(спираль
Архимеда).
,
заданной
в
полярных
координатах
(спираль
Архимеда).
17.7.
Под
каким
углом пересекаются
кривые
![]() и
и
![]() в
точке
в
точке
![]() ?
?
17.8.
Для данной
кривой
в
данной
точке
составьте
уравнения
касательной
и
нормали:
1)
![]() ,
, ![]() ;
2)
;
2)
![]() ,
, ![]() ,
, ![]() .
.
Домашнее задание 17.
17.9.
Для данной
кривой
в
данной
точке
составьте
уравнения
касательной
и
нормали:
1)
![]() ,
, ![]() ;
2)
;
2)
![]() ,
, ![]() ,
, ![]() .
.
17.10.
Определите, в какой точке и под каким
углом пересекаются кривые:
1)
![]() и
и
![]() ;
2)
;
2)
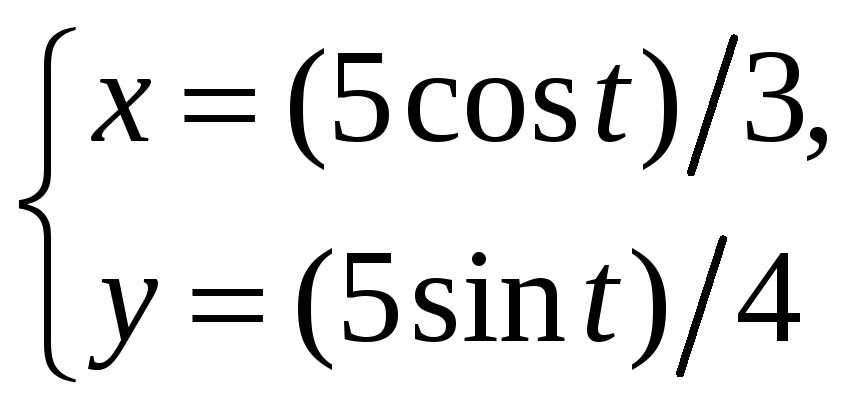 и
и
![]() .
.
17.11.
Найдите
дифференциал
функции
![]() в
данной
точке:
1)
в
данной
точке:
1)
![]() ,
, ![]() ;
2)
;
2) ![]() ,
, ![]() ;
3)
;
3) ![]() ,
, ![]() ,
, ![]() .
.
Занятие 18.
Производные и дифференциалы высших порядков.
Правило Лейбница.
Задачи
18.1.
Докажите, что функция
![]() удовлетворяет уравнению
удовлетворяет уравнению
![]() .
.
18.2.
Вычислите дифференциал второго порядка
функции
![]() в
точке
в
точке
![]() .
.
18.3.
Найдите
![]() для функции, заданной:
1)
параметрически
для функции, заданной:
1)
параметрически
![]() ,
,
![]() ;
2)
неявно
;
2)
неявно
![]() .
.
18.4.
Найдите
![]() і
і
![]() ,
если
,
если
![]() и
и
![]() – известные
функции
от
– известные
функции
от
![]() ,
если:
1)
,
если:
1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() .
.
18.5.
Найдите
![]() для функции
для функции
![]() .
.
18.6.
Найдите
![]() для функции
для функции
![]() .
.
18.7.
Найдите
![]() функции
функции
![]() .
.
18.8.
Найдите
![]() (
(![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() – считаются
известными)
для
функции
– считаются
известными)
для
функции
![]() .
.
Домашнее задание 18.
18.9.
Докажите, что функция
![]() удовлетворяет уравнению
удовлетворяет уравнению
![]() .
.
18.10.
Вычислите дифференциал второго порядка
функции
![]() в
точке
в
точке
![]() .
.
18.11.
Найдите
![]() для функции, заданной:
1)
параметрически
для функции, заданной:
1)
параметрически
![]() ,
,
![]() ;
2)
неявно
;
2)
неявно
![]() .
.
18.12.
Найдите
![]() і
і
![]() ,
если
,
если
![]() и
и
![]() – известные
функции
от
– известные
функции
от
![]() ,
если
,
если
![]() .
.
18.13.
Найдите
![]() для функции
для функции
![]() .
.
18.14.
Найдите
![]() для функции
для функции
![]() .
.
18.15.
Найдите
![]() функции
функции
![]() .
.
18.16.
Найдите
![]() (
(![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() – считаются
известными)
для
функции
– считаются
известными)
для
функции
![]() .
.
Занятие 19. Правило Лопиталя.
Задачи
19.1.
Найдите:
1)
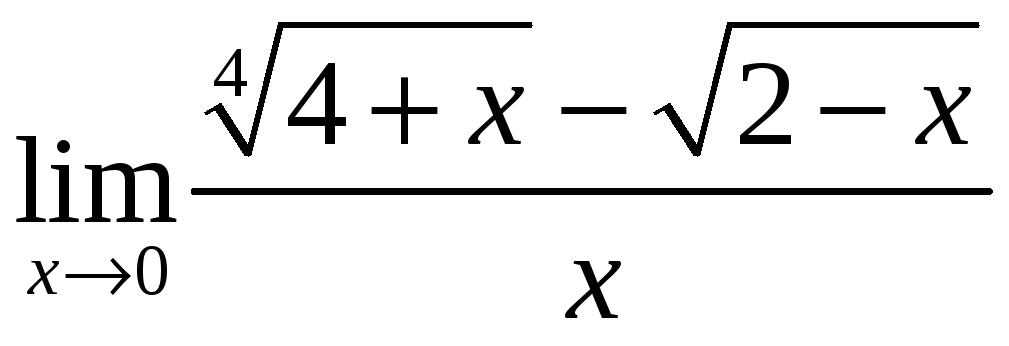 ;
2)
;
2)
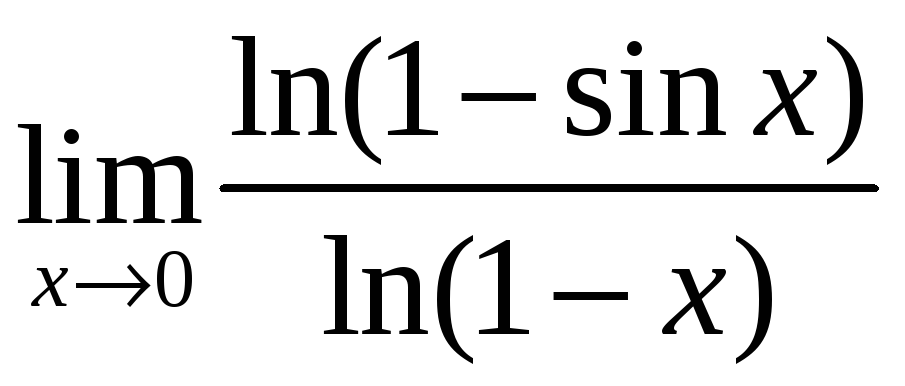 ;
3)
;
3)
![]() ;
4)
;
4)
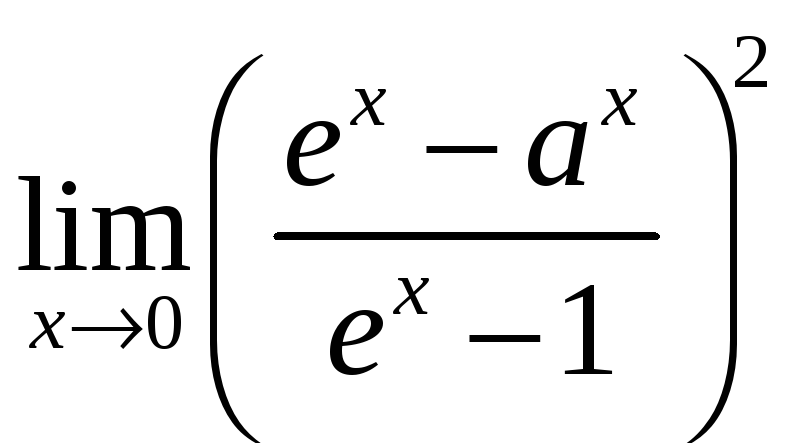 ,
,![]() ;
5)
;
5)
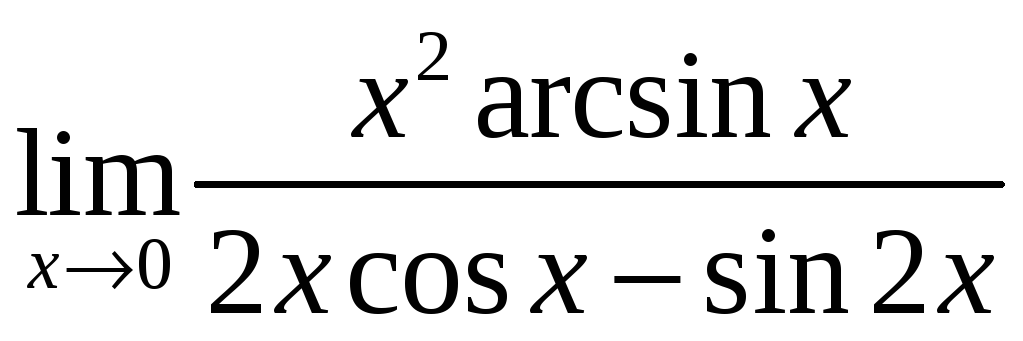 ;
6)
;
6)
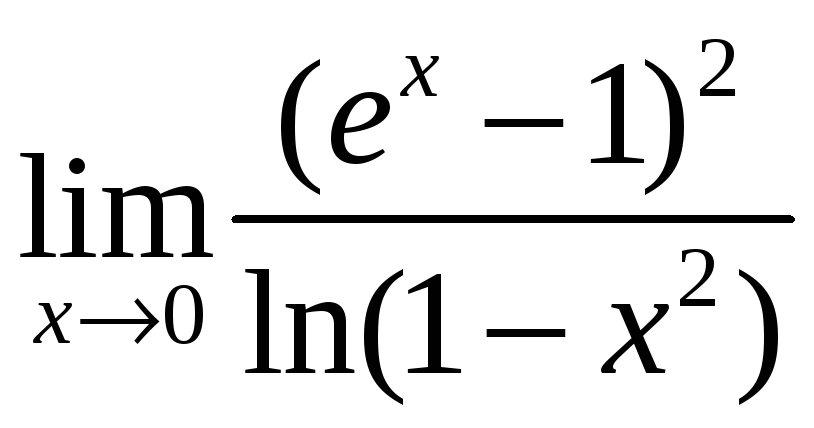 .
.
19.2.
Найдите пределы, преобразовав
предварительно выражения:
1) ![]() ;
2)
;
2) ![]() ;
3)
;
3) ![]() ,
,![]() ,
,
![]() .
.
19.3.
Найдите
пределы
при
помощи
формулы
![]() :
1)
:
1)
![]() ;
2)
;
2)
![]()
19.4.
Найдите: 1)
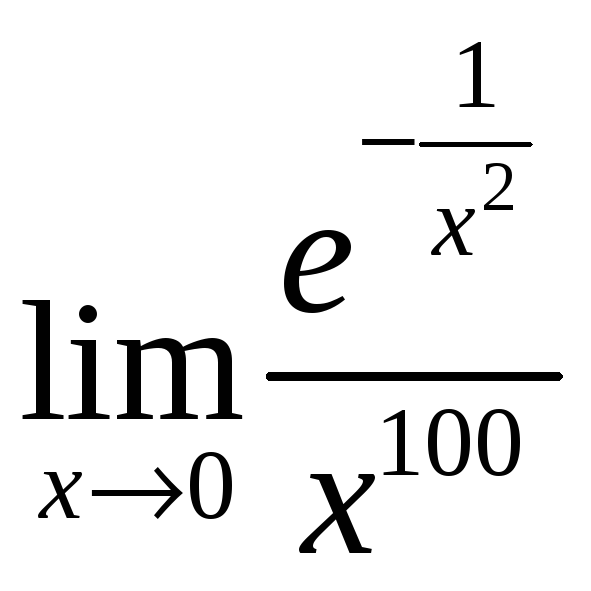 ;
2)
;
2)
![]() ;
3)
;
3)
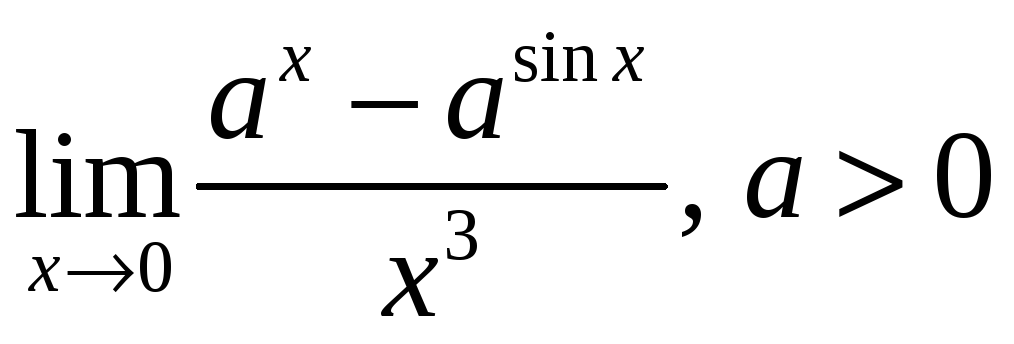 .
.
Домашнее задание 19.
19.5.
Найдите: 1)
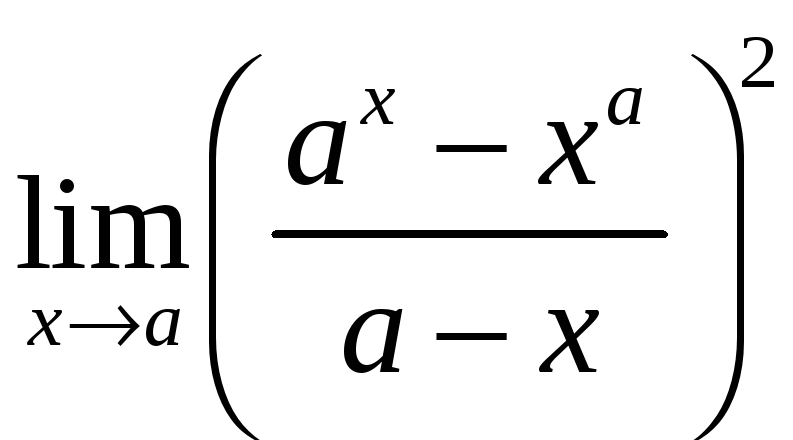 ,
,![]() ,
,
![]() ;
2)
;
2)
![]() ;
3)
;
3)
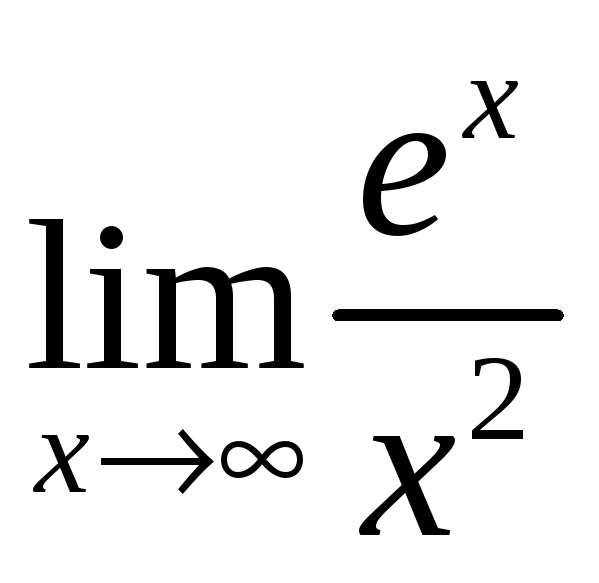 ;
4)
;
4)
![]() .
.
19.6.
Найдите пределы, преобразовав
предварительно выражения:
1) ![]() ;
2)
;
2) ![]() .
.
19.7.
Найдите
пределы
при
помощи
формулы
![]() :
1)
:
1)
![]() ;
2)
;
2)
![]() .
.
Занятие 20. Контрольная работа №2. Самоподготовка.
1) Вычислите:
а)
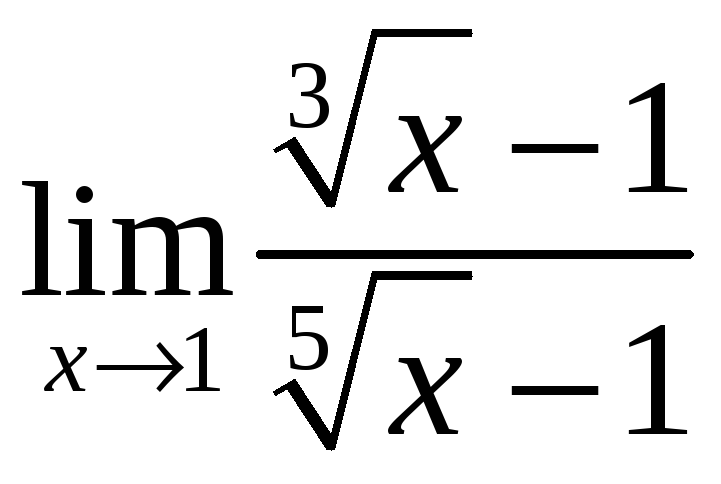 ;
б)
;
б)
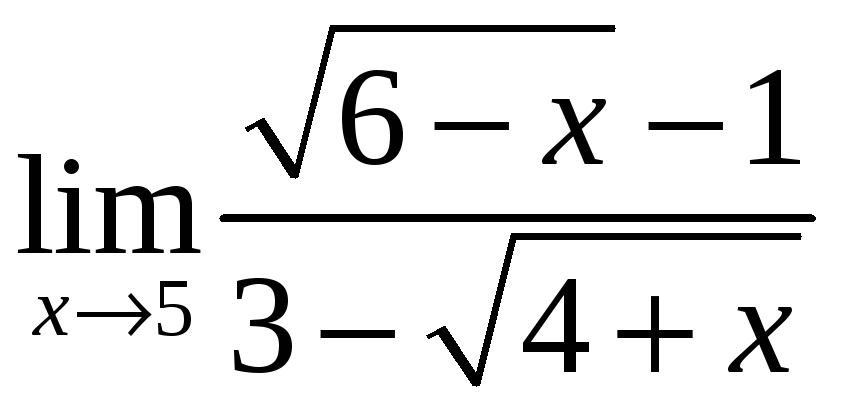 ;
в)
;
в)
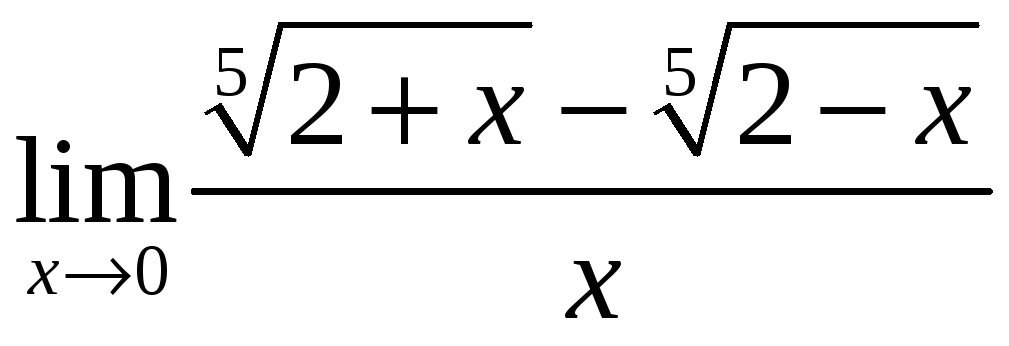 ;
г)
;
г)
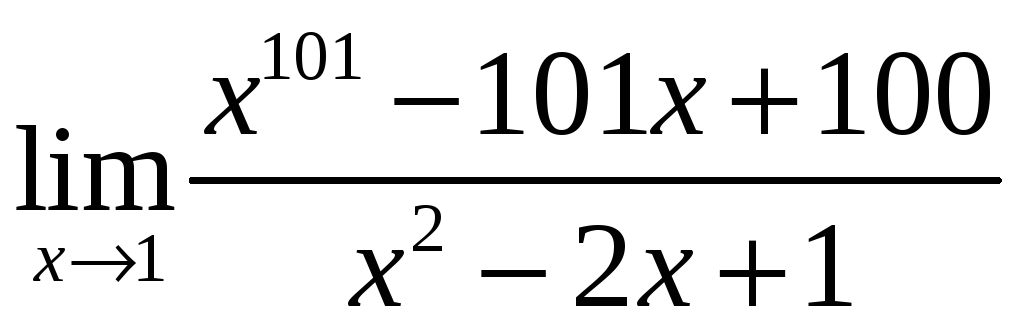 ;
д)
;
д)
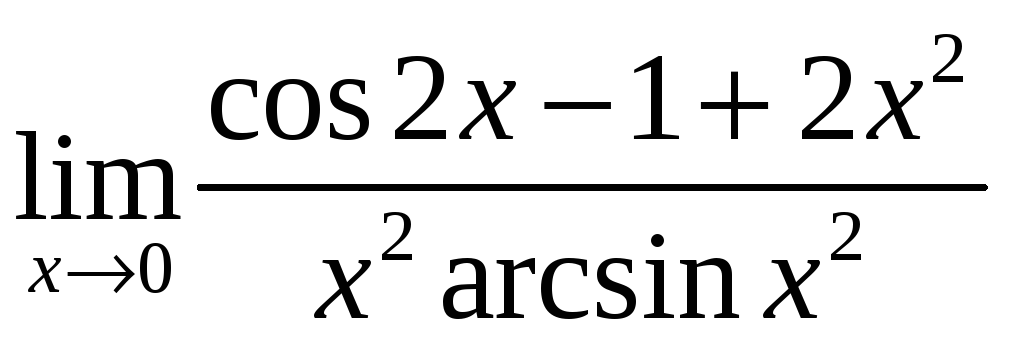 ;
е)
;
е)
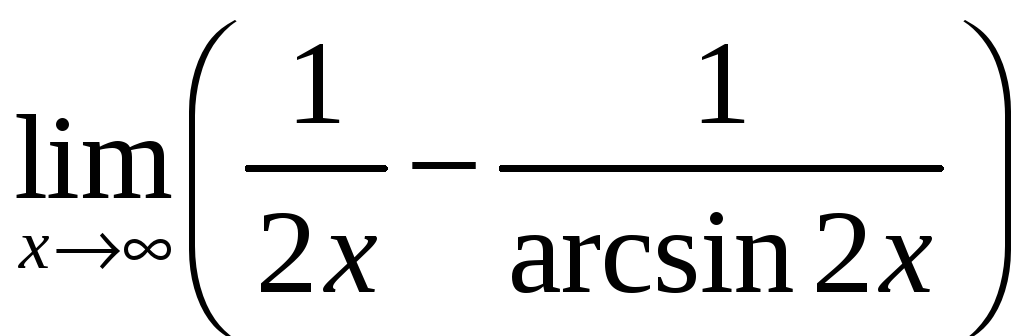 .
.
2)
Вычислите:
а)
![]() ;
б)
;
б)
 ;
в)
;
в)
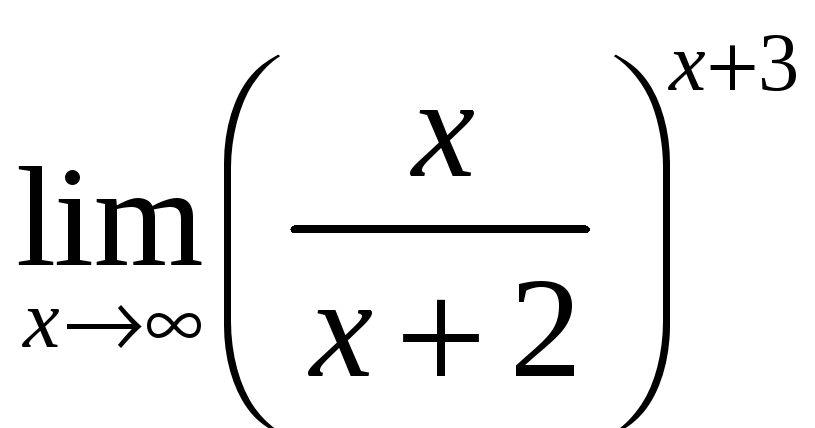 ;
г)
;
г)
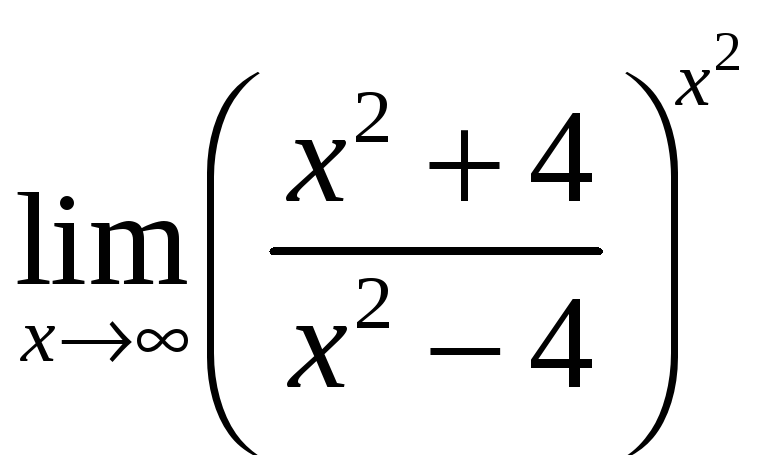 ;
д)
;
д)
![]() ;
е)
;
е)
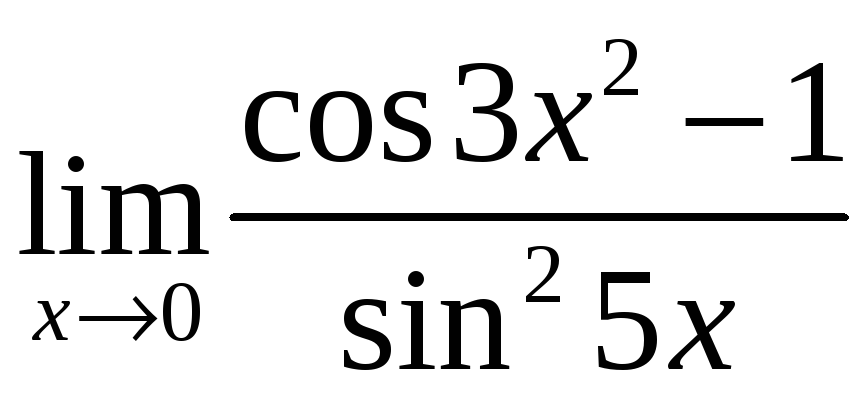 .
.
3)
а) При
каких
![]() функция
функция
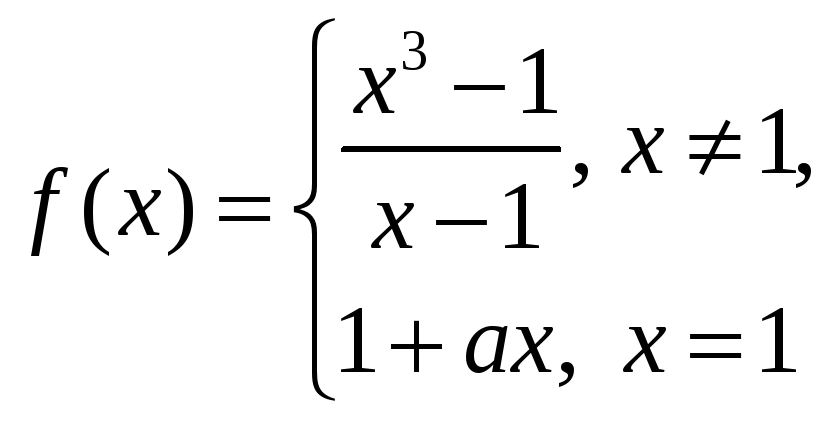 непрерывна в точке
непрерывна в точке
![]() ?
б)
Существует ли значение
?
б)
Существует ли значение
![]() ,
при котором
функция
,
при котором
функция
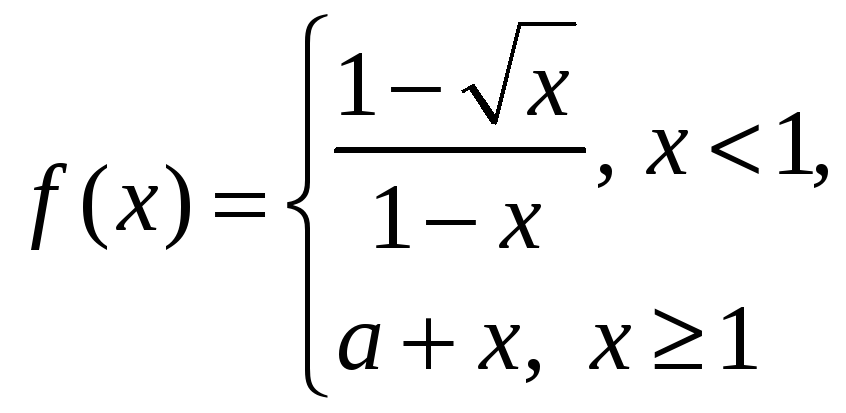 непрерывна
в
точке
непрерывна
в
точке
![]() ?
в)
Существуют
ли значения
?
в)
Существуют
ли значения
![]() и
и
![]() ,
при
которых
функции
,
при
которых
функции
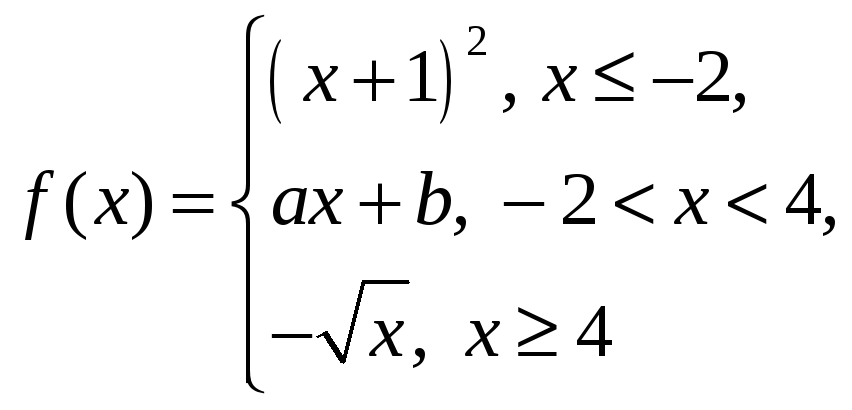 и
и
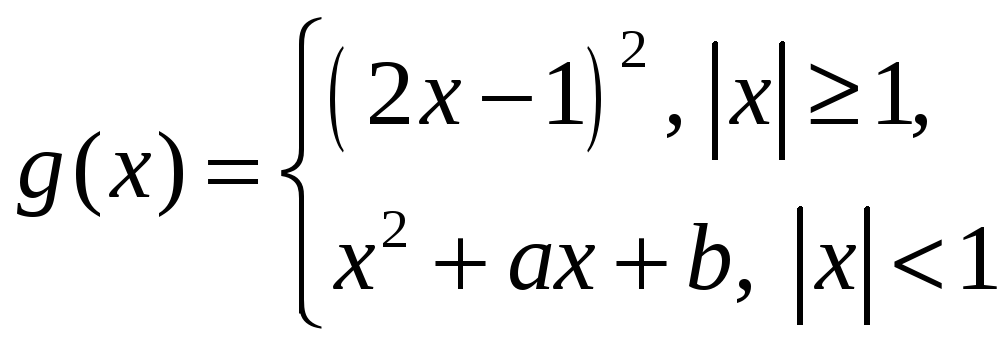 непрерывны
на своих
областях
определения?
непрерывны
на своих
областях
определения?
4)
Вычислите
производную:
а)
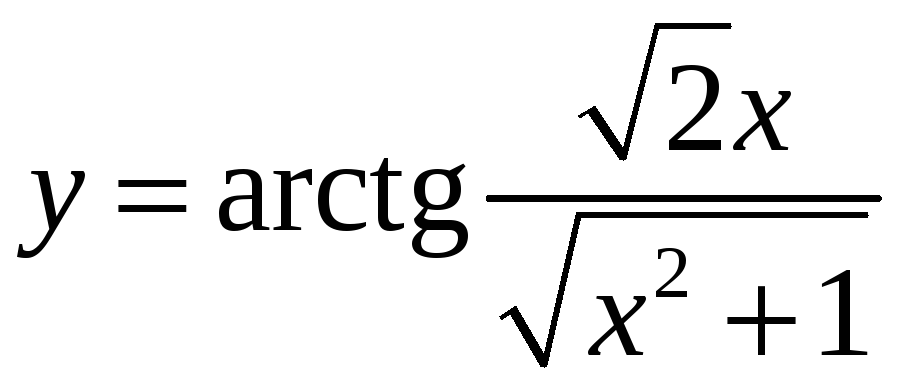 ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
 ;
д)
;
д)
![]() .
.
5)
Напишите
уравнения
касательной
и
нормали
к
кривой
:
а)
![]() в
точке
в
точке
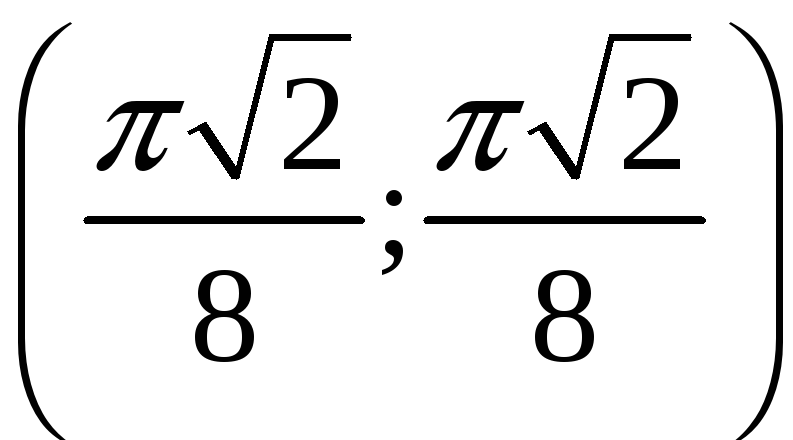 ;
б)
;
б)
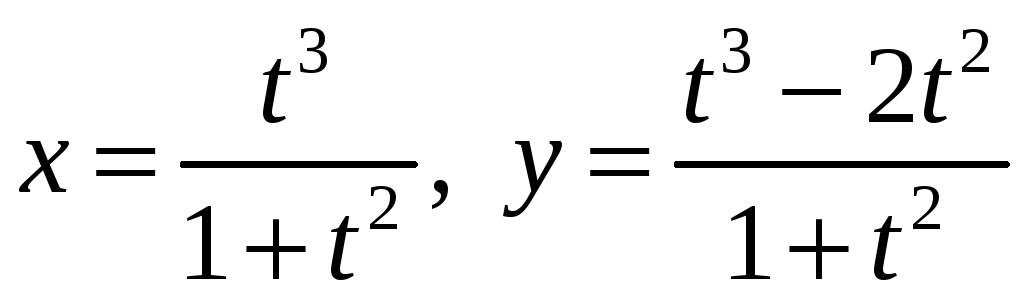 в
точке
в
точке
![]() ;
в)
;
в)
![]() в
точке
в
точке
![]() .
.
6)
Найдите:
а)
![]() –ю
производную
функции
–ю
производную
функции
![]() ;
б)
;
б)
![]() для функции
для функции
![]() .
.
