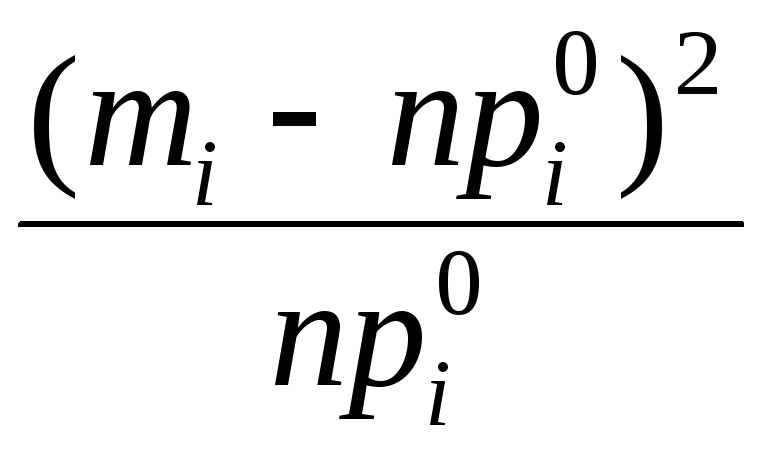5. Сравнение долей

Мы уже рассмотрели общий вопрос сравнения двух выборок:

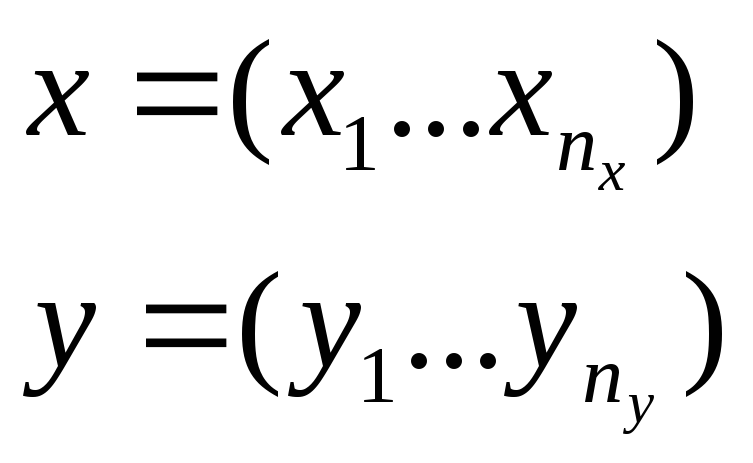
здесь - наблюдаемые значения.

Рассмотрим теперь частный, но чрезвычайно важный для лингвистики вопрос о сравнении долей (или частот): ,частоты, объем выборки.

Итак, доля - -это часть, занимаемая фактами в общем ряду наблюдений.

Например, при 100 бросаниях монеты "Г" выпал 60 раз или если была сделана выборка в 1000 слов и в ней 250 глаголов, то доля глаголов в выборке (или 25).

Доли как и частоты, колеблются (варьируют) около некоторой средней величины, выражая действие закона вероятности.

Среднее квадратическое отклонение доли, которое характеризует разброс доли вокруг среднего, определяется, как

,где длина (объем выборки).

применяется для сравнения долей одного и того же признака (явления) в 2 разных статистических совокупностях наблюдений. Например, можно сравнить долю всех сказуемых среди всех членов предложения в произведениях Л. Толстого и Шолохова, в двух главах одного и того же произведения и т.д.

Для решения подобных статистических задач рассматривается формула среднего квадратического отклонения:

, где ,

длина1-ой выборки,длина 2-ой выборки.

Например, Толстого, Шолохова.

Пример. Взяты 2 текстовые выборки, каждая длины в 1000 слов ; в первой выборке 200 глаголов, во второй-150.Можно ли считать равенство долей глаголов в первой и второй выборках? Т.е. их различие обусловлено только случайностью?

Имеем:

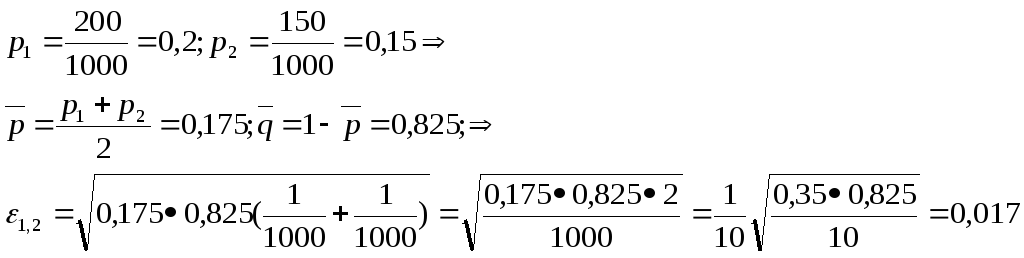
Метод: сравнивается с разностью . Если гипотезу о равенстве и следует отвергнуть, т.е. расхождение долей существенно.

У нас: . Мы можем отвергнуть гипотезу о случайности расхождения долей.

Второй метод: Критерий

Формула:

где и выборочные частоты,

Если , т.е. одинаковый объем, то

где: ; а число степеней свободы .

Итак, можно сравнить частоты, можно доли. Можно делать вывод о сходимости и различий языковых и речевых степеней, участков речевых структур в разные эпохи и у разных народов. Так можно сравнивать доли имен и глаголов в стилях, научном и художественном, у Пушкина и Блока, в языках русском и марийском, в русском языке XIV и XX веках и т. д.

Чем больше устойчивость частот, чем реже они существенно отличаются от средней, тем надежнее действие того статистического закона, внешнее проявление которого и показывает частоты с их колебаниями.

Задача

Проверить гипотезу о нормальном распределении ГС по выборке В при уровне значимости

Значения :

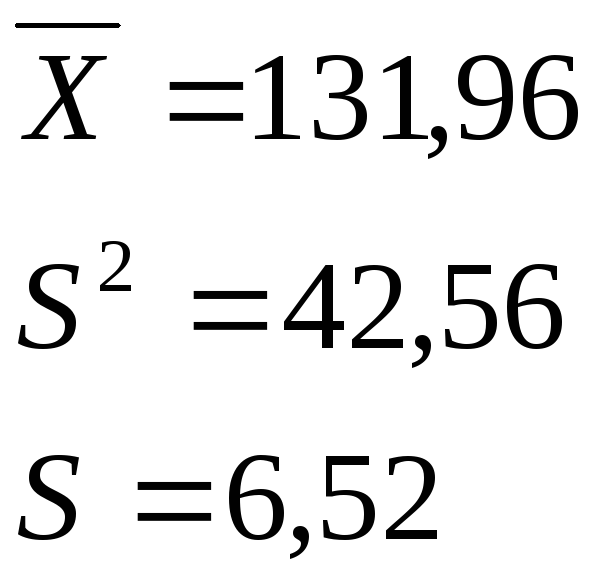
Пусть имеется 190 наблюдений: . Эти наблюдения структурированы следующим образом:

1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11.	(112-116] (116-120] (120-124] (124-128] (128-132] (132-136] (136-140] (140-144] (144-148] (148-152] (152-156]	2 3 15 31 46 40 36 12 3 1 1	0,011 0,016 0,079 0,163 0,242 0,211 0,189 0,063 0,016 0,005 0,005
		190	1,000

частота попадания в интервал.

выборка Г.С.

Если бы мы просмотрели всю ГС, то смогли бы определить распределение наблюдаемого признака. Но, поскольку мы не имеем возможности просмотреть всю ГС, то о значении изменения признака мы можем судить лишь по выборке.

Чтобы понять какое распределение может иметь признак, т.е. какую стоит поставить гипотезу, сделаем предварительную обработку результатов наблюдения. Построим для этого гистограмму.

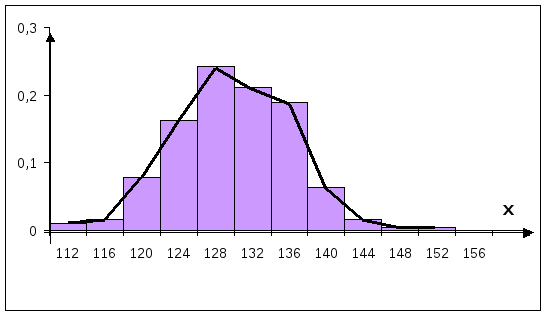
Построение гистограммы показывает, что распределение близко к нормальному, поэтому мы можем выдвинуть гипотезу о нормальности распределения определенного признака , нормальная случайная величина.

Итак, выдвинем гипотезу :

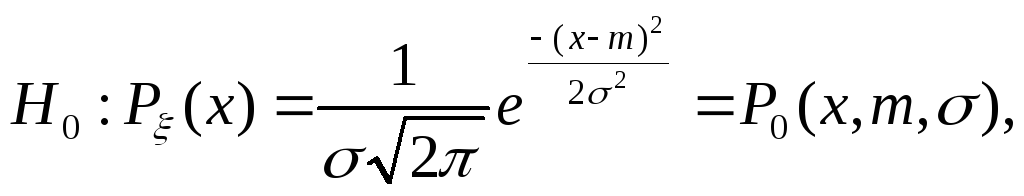где m и параметры нормального распределения.

Или ,

функция распределения случайной величины .

Мы поставили гипотезу , тем самым считая, что наш признак имеет в действительности заданное распределение при неизвестных пока параметрах и .

Как мы сказали, параметры и нашего гипотетически нормального распределения неизвестны и подлежат оценке по выборке:

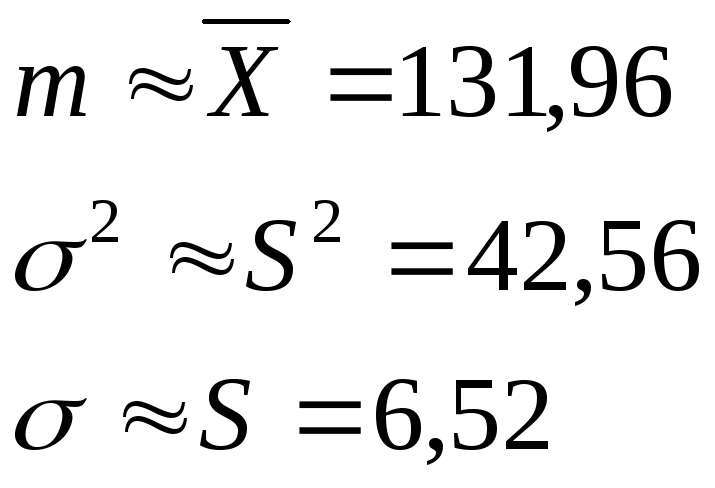
Теперь гипотеза принимает вполне конкретный вид .

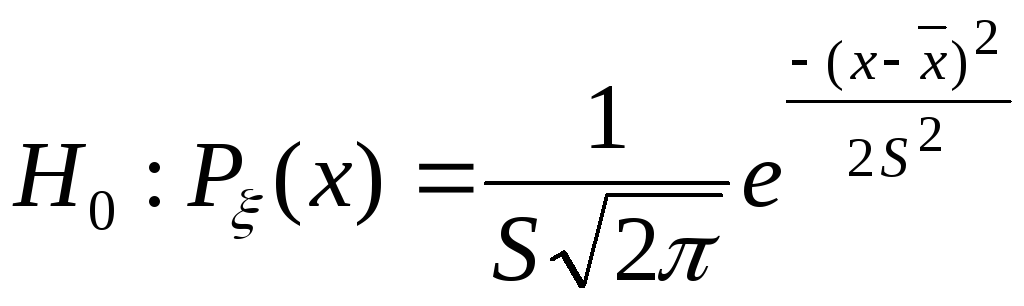Для проверки гипотезы воспользуемся критерием . Для этого нам надо сравнить два ряда - ряд вероятностей и ряд частот. Тогда, в силу закона больших чисел, если верна, то мы обязаны иметь близость вероятностей и частот.

А это мера расхождения этих двух наборов, на основании которой мы и будем судить велико ли различие между рядами вероятностей и частот. Если мера покажет , что расхождение велико , то гипотезу следует отвергнуть, а в противном случае - принять.

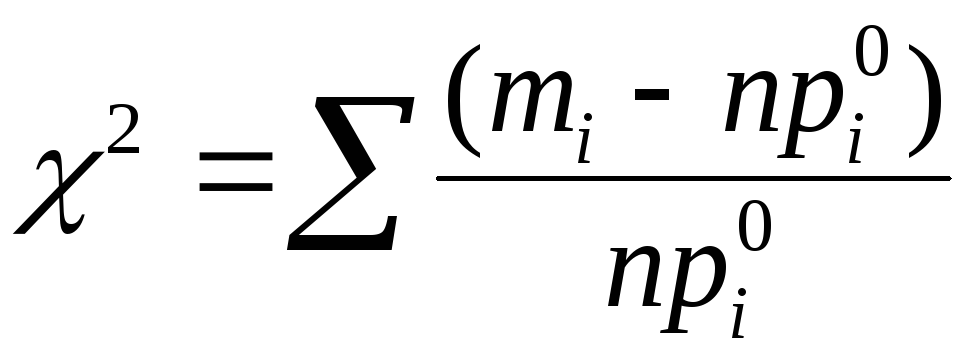
Сведем вычисления в таблицу:

1 2 3 4 5 6 7 8 9	- -1,83 -1,22 -0,61 0,01 0,62 1,23 1,85 +	0 0,0336 0,1112 0,2709 0,5040 0,7324 0,8907 0,9678 1	0,0336 0,0776 0,1596 0,2331 0,2284 0,1583 0,0771 0,0322	5 15 31 46 40 36 12 5	6,384 14,744 30,343 44,289 43,396 30,077 14,649 6,118	0,300 0,004 0,014 0,066 0,266 1,166 0,479 0,204

В вариационном ряде частоты первого и последних интервалов слишком малы, поэтому объединим их с соседними интервалами. В результате остается интервалов.

А левую и правую границы нам удобнее отнести в и в .

Если гипотеза верна, то (как мы отметили) ряд частот и ряд вероятностей должны быть близки друг к другу. Следовательно, будут близки друг к другу и ряды

т

np_i⁰

m_i

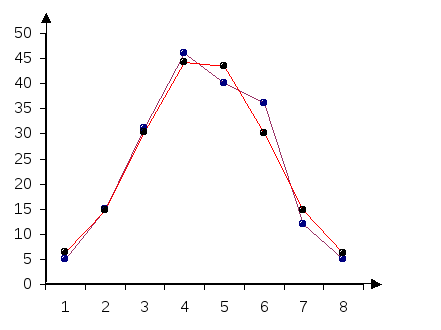
Из графического построения рядов видим, что ряды похожи, близки друг к другу. Чтобы понять, что ряды действительно близки друг к другу, а тогда верна, возьмем значение из таблицы. Это наша мера расхождения между двумя рядами: теоретическим и эмпирическим.

Теперь необходимо найти критическое из таблицы распределения.

Если будет , то принимается, в противном же случае – отвергается.

У нас:

принимается!

Опытные данные, на основе которых мы выдвинули гипотезу о нормальности распределения , в действительности не противоречат этой гипотезе.