Пример 1

Дважды бросается монета.

Пусть - число гербов. Очевидно, 0,1,2. Соображения симметрии подсказывают, что

	0	1	2

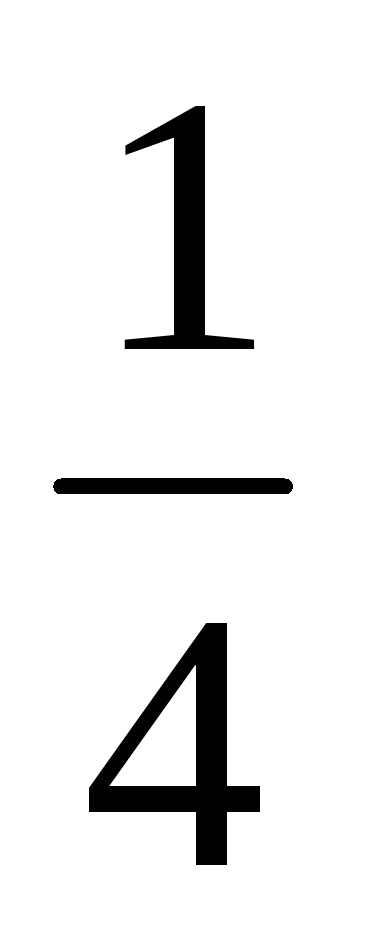
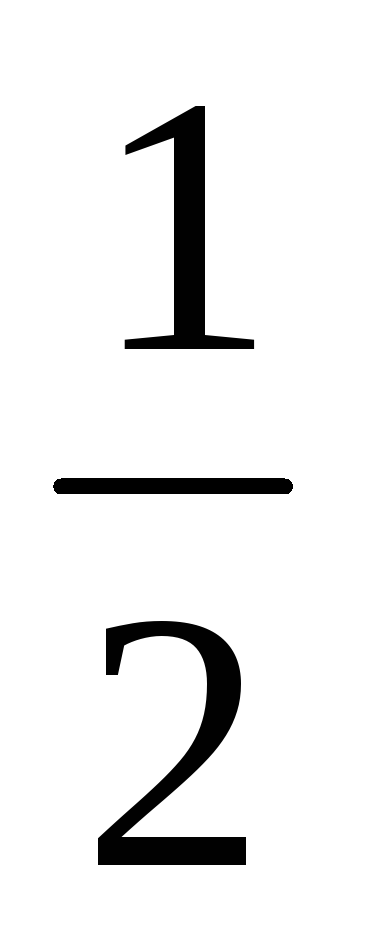
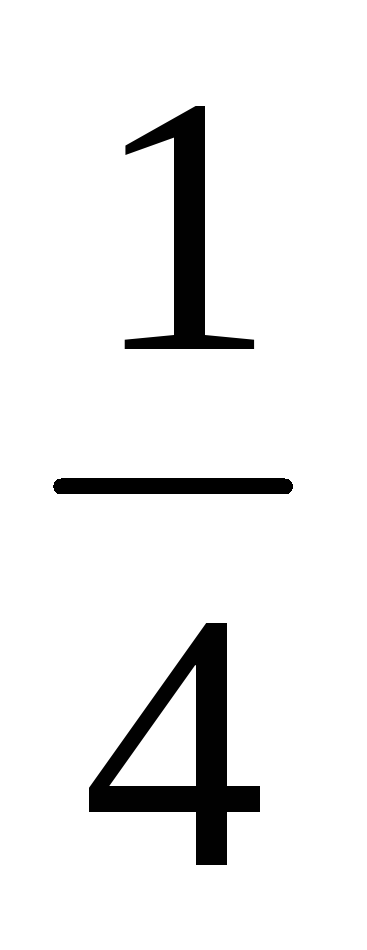
Пример 2.Монета бросается до первого появления герба. Ясно, что 1,2,.. . В этом случае имеем геометрический закон распределения: где - вероятность появления герба, - "решки", . Для симметричной монеты и

Итак набор {}или

			….
			….

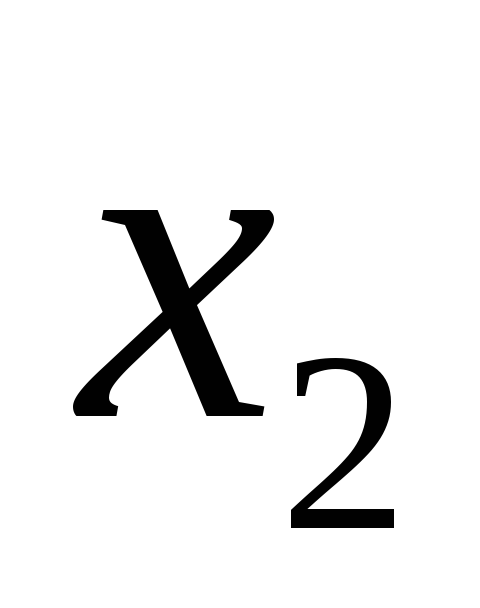
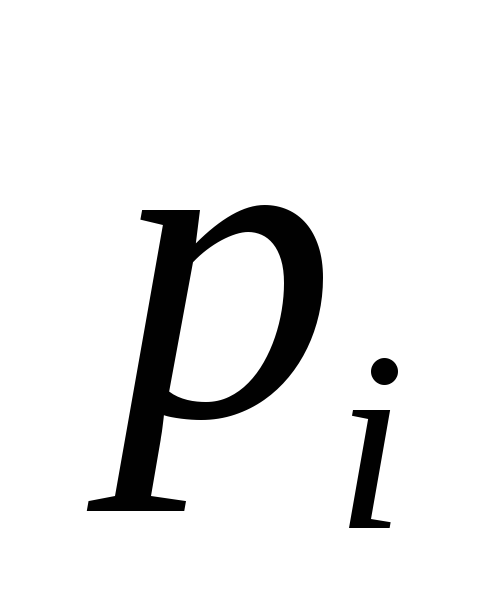
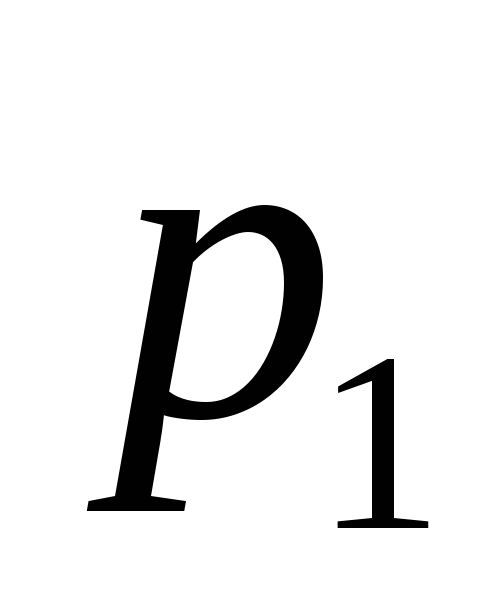
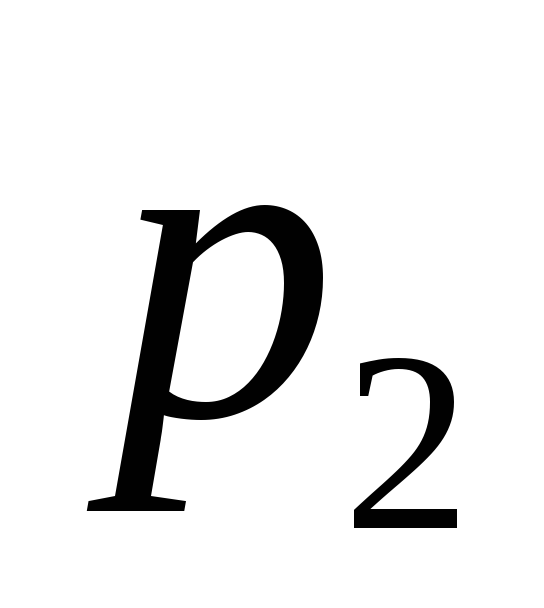
задают распределение вероятностей (закон изменения) изучаемого признака (с.в.). Существует несколько классических законов распределения дискретной с.в.: биномиальный, геометрический, равномерный, Пуассона и др.

Пример 3

Рассмотрим ГС - "Тихий Дон". Пусть - число слов в предложении. Для произвольно взятого предложения есть с.в. (нельзя предсказать заранее число слов в предложении). Обозначим - общее число предложений, - число предложений с числом слов (для "Тихого Дона"). Тогда число есть вероятность (частота) наблюдать предложение с числом слов . Поскольку просмотр всей ГС (всего "Тихого Дона") технически затруднителен, то мы можем говорить, что закон распределения {} неизвестен и поэтому естественна задача установления этого неизвестного теоретического распределения на основе выборки(),где -число предложений, -число слов в -ом предложении.

Непрерывные с.в. К таким признакам следует отнести те признаки, значения которых "заполняют" некоторый интервал. Например, время - непрерывный признак. Такие признаки (с. в.) будут использоваться нами в качестве "инструмента" при изучении физических признаков (очевидно, дискретных), рассматриваемых в языковых исследованиях. Закон изменения непрерывного признака задается некоторой функцией , которая удовлетворяет двум условиям:

а) - неотрицательность

б) - нормированность.

Если значения признака , то условия а) и б) примут вид:

и или

Итак, задавая функцию (удовлетворяющую условиям а) и б)), мы тем самым будем задавать некоторый закон изменения признака . Рассматривают классические законы распределения: нормальный, равномерный, Стьюдента, (хи-квадрат) и др. Они далее будут выступать в качестве вероятностно-статистического "инструмента" при изучении физических (очевидно, дискретных) признаков, применяемых при статистическом моделировании в языковых исследованиях.

Заметим, что распределение можно характеризовать также с помощью функции распределения (ф.р.) с.в.

Очевидно,

Графически выглядит следующим образом:

Задача 2 Случайная величина имеет ряд числовых характеристик:

- математическое ожидание (среднее значение),

- дисперсия,

- коэффициент ассиметрии,

- коэффициент эксцесса,

- вариация.

характеризует "центр" распределения, вокруг которого разбросаны значения признака . Дисперсия есть мера рассеяния признака относительно . В качестве относительного показателя разброса рассматривают вариации , что позволяет сопоставить с.в. различной размерности. Чтобы выразить степень ассиметрии распределения признака, применяют коэффициент ассиметрии . Если , то распределение имеет вытянутость влево (левосторонняя асимметрия), если , то - вправо, наконец, при имеет симметрическое распределение.

Теоретическое распределение признака может быть плоским или крутым, островершинным. Чтобы выразить степень крутизны, рассматривают коэффициент эксцесса:

.

Чем больше, тем более крутое распределение имеет признак . В качестве стандарта берется так называемое нормальное распределение, для которого , .

Плотность нормального распределения имеет вид:

Тогда:

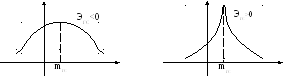
Обозначим - множество неизвестных параметров, характеризующих изучаемый признак , а, следовательно, и . Тогда возникает 2 основные задачи:

а) на основе результатов наблюдений оценить параметр (построить «точечную» оценку для );

б) если - точечная оценка для , то необходимо оценить точность оценки (интервальная оценка ).

Задача 3 Пусть - многомерный признак (случайная величина), т.е. . Тогда возникает важнейшая задача статистического анализа – исследование связей между признаками. Здесь мы имеем группу задач:

а) оценить тесноту связи между любой парой признаков и . В качестве меры тесноты связи рассматривают парный коэффициент корреляции . Мы могли бы найти , если бы просмотрели всю . Поскольку такой возможности нет, то задача состоит в нахождении оценки для , по результатам наблюдений , где уже двумерная выборка . Если - такая оценка, то вторая задача состоит в оценке по значению тесноты связи, т.е. мы должны сделать вывод о значимости (достоверности) или незначимости (недостоверности связи). Для этого существует статистическая процедура, позволяющая определить значимость при незначимости связи. Наконец, если мы по установили, что связь значимая, то возникает еще одна задача: найти вид этой связи в виде регрессионного уравнения

.

б) пусть - результирующий признак (выходная переменная), а - входные, объясняющие переменные, т.е. , где - «шум» процесса. Тогда возникают 2 задачи:

• установить, существует ли достоверная связь между и ;

• в случае достоверной связи, найти вид связи, т.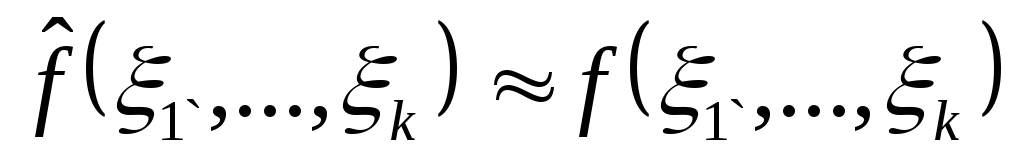е. , где неизвестна. Существуют статистические процедуры, реализованные на ЭВМ, позволяющие решать поставленные задачи.

В заключении пункта приведем еще один пример типичной задачи статистического анализа.

Пример 4 Монеты подбрасываются раз. Известно, что при этом «герб» выпал раз. Пусть - вероятность выпадения «герба».

А: Как оценить неизвестную вероятность - вероятность выпадения «герба»?

В: Если - оценка , то какова точность этой оценки?

С: Как проверить гипотезу о том, что монета симметрична ?

D: Как различить 2 гипотезы о том, что и . (Например, и ).