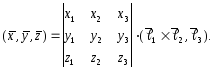§ 5. Скалярное, векторное и смешанное произведения векторов

Скалярным произведением двух векторов и , как известно, называют число, определяемое формулой

. (1)

Можно проверить, что скалярное произведение обладает следующими свойствами:

1) 2)

3)

4) , .

Из (1) также следует, что

прпр. (2)

Запись пр означает проекцию вектора на направление вектора

Рассмотрим ортонормированный базис

Очевидно

. (3)

Пусть

Используя свойства скалярного произведения и учитывая (3), найдем выражение скалярного произведения через координаты перемножаемых векторов в ортонормирован-ном базисе.

(4)

Если то из (4) найдем, что

Пример 1. Вычислить работу силы при перемещении материальной точки из пункта в пункт .

Решение. Работа

Поскольку

то

Базис называют правым, если поворот первого вектора ко второму на наименьший угол между ними со стороны третьего кажется против стрелки часов. В противном случае базис называют левым.

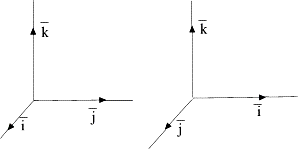
На первом рисунке базис правый, а на втором левый. В дальнейшем будем пользоваться правым базисом.

Определение 1. Векторным произведением двух векторов и называют третий вектор , удовлетворяющий следующим требованиям:

1) вектор перпендикулярен векторам и ;

2) тройка векторов ,, правая;

3) модуль векторного произведения равен площади параллелограмма, построенного на перемножаемых векторах, т.е.

Обозначают векторное произведение так

Рассмотрим ортонормированный базис .

Согласно определению векторного произведения найдем:

, , ,

, , . (5)

Отметим следующие свойства векторного произведения.

1. 

2. 

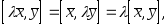
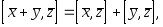3. 4)

Используя свойства векторного произведения и соотношения (5), найдем векторное произведение двух векторов , , заданных в ортогональном базисе своими координатами.

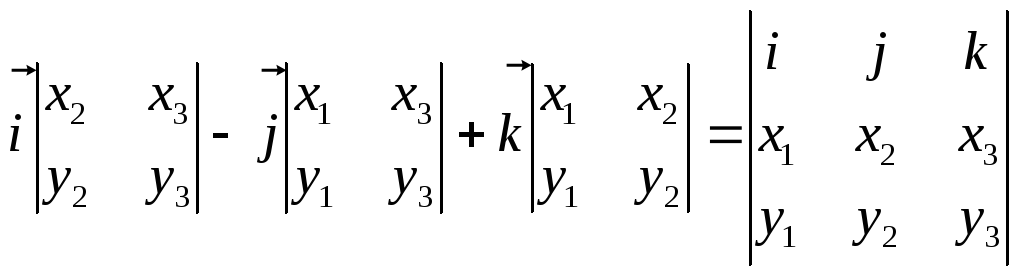=. (6)

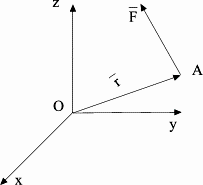
Пример 2. Найти момент силы приложенной в точке , относительно начала координат.

Решение. =

= .

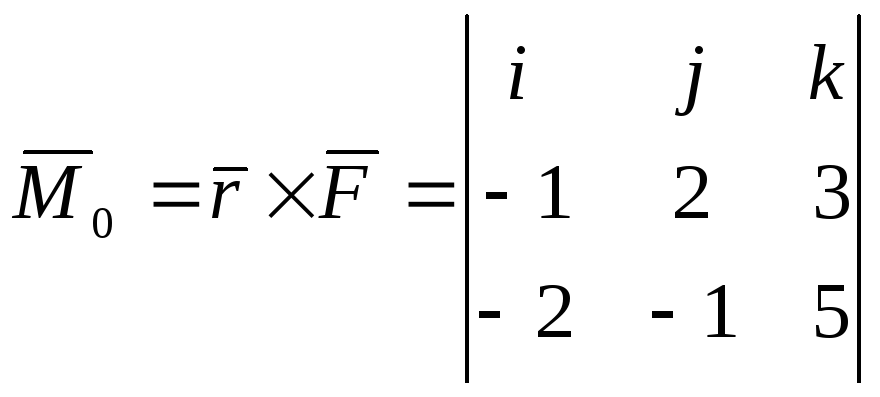Определение 2. Смешанным произведением трех векторов ,, называют число, равное

Рассмотрим геометрический смысл смешанного произведе-ния. Векторы ,, выберем в качестве ребер и построим параллелепипед. Пусть тогда -площадь основания паралле-лепипеда, а смешанное произведение

Здесь H - высота параллелепипеда, а V – его объем.

Таким образом, смешанное произведение только знаком может отличаться от объема параллелепипеда, построенного на перемножаемых векторах как на ребрах. Если тройка правая, то знак смешанного произведения будет положительным.

Из геометрического смысла смешанного произведения ясно, что векторно можно перемножать любые два из трех векторов, от этого может измениться только знак. Легко проверить, что тройки векторов , и одинаковой ориентации, так что = = = Поэтому смешанное произведение обозначают не указывая, какие векторы перемножаются векторно.

Выразим смешанное произведение через координаты перемножаемых векторов в ортонормированной системе координат.

Пусть

Поскольку, то

=

= . (7)

Теорема. Необходимым и достаточным условием компланарности трех векторов является равенство нулю их смешанного произведения.

Доказательство ясно из геометрической интерпретации смешанного произведения.

Следствие. Три вектора линейно независимы только в том случае, если их смешанное произведение отлично от нуля.

Доказательство очевидно.

Пример 3. Проверить линейную независимость векторов (см. пример §4).

Решение. Найдем их смешанное произведение 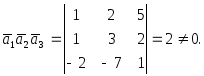Данные векторы, согласно следствию, линейно независимые.

Обобщим понятие вектора. Назовем вектором упорядоченную совокупность n действительных чисел, т.е.

вектор, его координаты.

При сложении векторов их соответствующие координаты будем складывать, а при умножении на число- умножать на это число.

Множество всех таких векторов с определенными выше операциями называют арифметическим пространством и обозначают Обычное пространство геометрических векторов обозначают множество компланарных геометрических векторов - коллинеарных -

Зафиксировав в пространстве ортонормированный базис , понятия скалярного, векторного и смешанного произведений можно обобщить и на векторы этого пространства

Cкалярным произведением двух векторов и пространства назовем число, определяемое следующей формулой . (8)

Векторным произведением (n–1) вектора пространства назовем вектор S этого же пространства, определяемый следующей формулой (5).

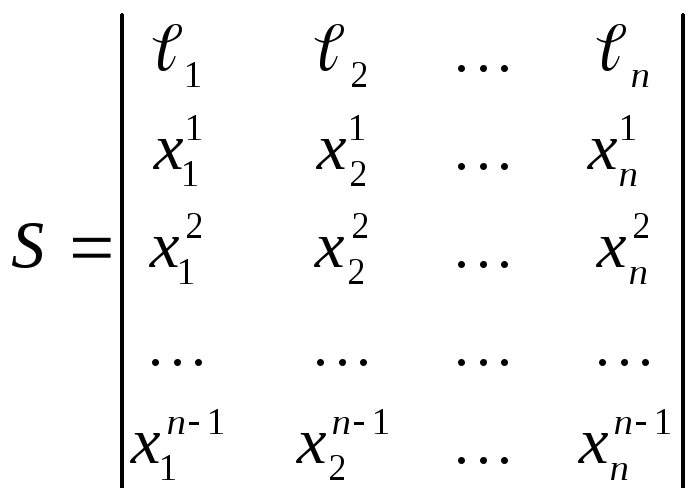. (9)

. (10)

Смешанным произведением n векторов пространства назовем число V, определяемое формулой (10).

Упражнение. Убедиться, что скалярное, векторное и смешанное произведения геометрических векторов , , , заданных своими координатами в некотором не ортогональном базисе имеют вид:

28