§ 2. Тригонометрическая и показательная формы комплексного числа

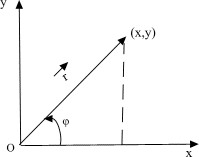
Как уже отмечалось, геометрической интерпрета-цией комплексного числа является точка на плоскости. Положение точки определяется ее радиус-вектором . В декартовой системе координат положение точки определяют ее координаты и . В полярной системе координат положение точки определяют координаты: – угол между осью и радиус-вектором и расстояние от начала координат до точки. Связь между декартовыми и полярными координатами следующая:

, . Учитывая это, комплексное число можно записать в виде

(1)

Формула (1) дает еще одну форму записи комплексного числа - тригонометрическую. При этом называется модулем комплексного числа, а угол - аргументом комплексного числа. Заметим, что угол определяется не однозначно, а с точностью до периода , поэтому вводят понятие главного значения аргумента -. Так что , .

Будем считать, что , тогда

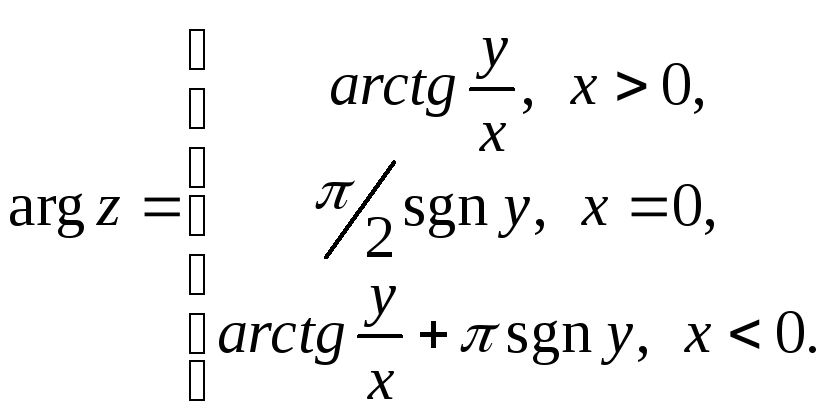где

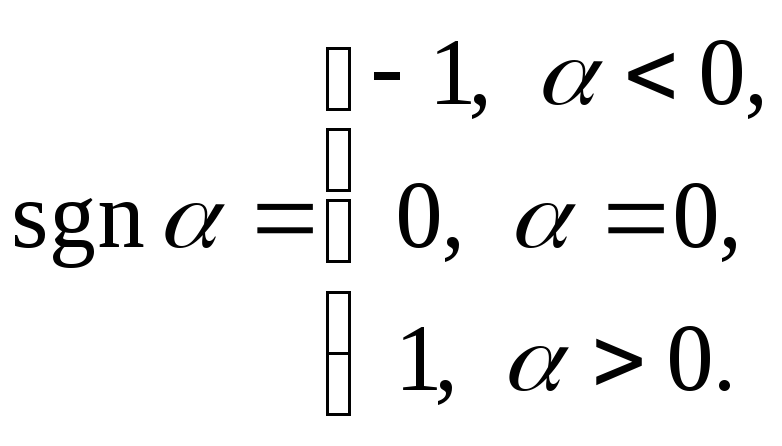
Пример 1. Представить числа , в тригонометрической форме.

Решение.

Умножим два комплексных числа, записанные в тригонометрической форме.

(2)

Как видно из формулы (2), при умножении чисел их модули перемножаются, а аргументы складываются. Правило это распространяется на любое число сомножителей. В частности, если получим

(3)

Формула (3) называется формулой Муавра.

Аналогично можно убедиться, что при делении чисел их модули делятся, а аргументы вычитаются (убедиться в этом самостоятельно).

Рассмотрим действие извлечения корня n-ой степени (n – натуральное) из комплексного числа. Предположим, что в результате извлечения этого корня получится опять некоторое комплексное число.

Найдем неизвестные и . Для этого возведем обе части полученного равенства в n-ю степень. Используя формулу Муавра, получим, что

(4)

Равные комплексные числа имеют равные модули, а аргументы отличаются на . Поэтому из (4) следует

; .

Итак, (5)

Можно убедиться, что формула (5) дает ровно n различных корней при .

Пример 2. Найти .

Решение.

При получаются корни

,

, .

При k = 3 что совпадает с . Все последующие корни будут повторяться, так что различных корней будет только три.

Положим по определению для всех вещественных y

(6)

Формула (6) называется формулой Эйлера, – иррациональное число, основание натурального логарифма. Используя формулу Эйлера и предполагая верными обычные правила действия со степенями, найдем

(7)

Замечание 1. Формула (7) определяет функцию комплексного переменного z . Функция эта периодическая с периодом .

Действительно,

т.е..

Используя формулу Эйлера, получим еще одну форму записи комплексного числа- показательную.

(8)

Назовем логарифмом числа z комплексное число такое, что Таким образом, Пусть тогда

. (9)

Найдем модуль и аргумент числа .

Тогда очевидно Из равенства комплексных чисел (9) получим Следовательно,

. (10)

Замечание 2. Формула (10) определяет функцию комплексного переменного правда, эта функция многозначна, т.к. одному значению аргумента z она ставит в соответствие бесконечное множество значений функции.

Можно убедиться в справедливости обычных правил логарифмирования. В частности , . Однако, в силу многозначности логарифмической функции .

Пример 3. Найти

Решение. Согласно формуле (10)

Рассмотрим теперь возвышение комплексного числа в любую комплексную степень. По определению положим

. (11)

Пример 4. Найти

Решение. Согласно формуле (11) и результату примера 3, получим

Пример 5. Найти

Решение.