
- •Глава 1. Векторная алгебра и аналитическая геометрия. Элементы линейной алгебры
- •§ 1. Расширение понятия числа. Комплексные числа, действия над ними
- •§ 2. Тригонометрическая и показательная формы комплексного числа
- •§ 3. Понятие матрицы и определителя. Свойства определителей
- •4. (Правило сложения определителей).
- •§ 4. Геометрические векторы, линейная зависимость, базис
- •§ 5. Скалярное, векторное и смешанное произведения векторов
4. (Правило сложения определителей).
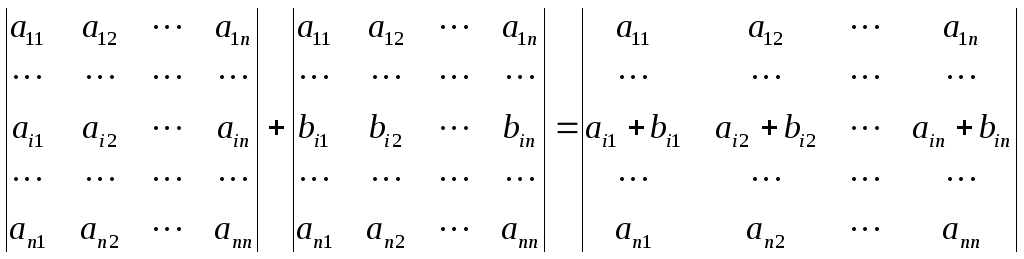 Доказательство
следует из теоремы Лапласа. Раскрывая
определители в левой и правой частях
равенства по элементам i-ой строки,
получим одно и то же.
Доказательство
следует из теоремы Лапласа. Раскрывая
определители в левой и правой частях
равенства по элементам i-ой строки,
получим одно и то же.
Следствие. Определитель не изменится, если к элементам некоторой строки добавить соответственные элементы другой строки, умноженные на одно и то же число.
Доказательство. Представим полученный определитель в виде суммы двух определителей согласно свойству 4. Первый определитель совпадает с данным, а второй будет содержать пропорциональные строки и следовательно равен нулю.
5.
Сумма
произведений элементов некоторой строки
на соответствующие алгебраические
дополнения другой строки равна нулю,
![]() ,
,
![]() .
.
Доказательство.
Рассмотрим два определителя
![]() и
и
![]() ,
которые отличаются только k-ой строкой.
,
которые отличаются только k-ой строкой.
 ;
;
 .
.
Если
раскрывать определители по k-ой строке,
то алгебраические дополнения
![]() ,
будут одинаковыми для обоих определителей.
,
будут одинаковыми для обоих определителей.
![]() . (4)
. (4)
Положим
теперь
![]() ,
,
![]() т.е. заменим k-ю строку определителя на
i-ю. Тогда определитель будет иметь две
одинаковые строки и обратится в нуль.
т.е. заменим k-ю строку определителя на
i-ю. Тогда определитель будет иметь две
одинаковые строки и обратится в нуль.
Из
(4) найдем
![]() ч.
т. д.
ч.
т. д.
Таким
образом,
![]() , (5)
, (5)
где
![]()
![]() – символ Кронекера.
– символ Кронекера.
6. Если в квадратной матрице строки сделать соответствующими столбцами, т.е. транспонировать матрицу, то ее определитель не изменится (без доказательства).
Следствие. Все предыдущие свойства и следствия, верные для строки, верны и для столбца.
Пример.
Вычислить определитель
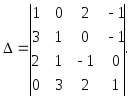
Решение. Используя свойства определителей, получим в первой строке еще два нуля.
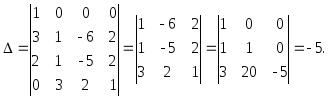
§ 4. Геометрические векторы, линейная зависимость, базис
Геометрическим вектором, как известно, называют направленный отрезок. Он характеризуется своей длиной (модулем) и направлением.
В математике изучают так называемые свободные векторы. Свободные векторы считаются равными, если их модули равны, а направления одинаковые. В физике, однако, важна точка приложения вектора (силы) или линия действия вектора (момента силы). Такие векторы не являются свободными. Это, соответственно, связанные и скользящие векторы.
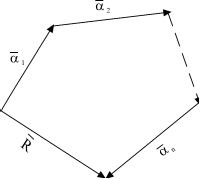
![]()
При
умножении вектора
![]() на
число
на
число
![]() его модуль увеличивается (уменьшается)
в
его модуль увеличивается (уменьшается)
в
![]() раз, а направление не изменяется, если
раз, а направление не изменяется, если
![]() .
Если
.
Если
![]() то направление изменяется на
противоположное. В любом случае векторы
то направление изменяется на
противоположное. В любом случае векторы
![]() и
и
![]() лежат на одной прямой (или на параллельных
прямых). Такие векторы называют
коллинеарными.
лежат на одной прямой (или на параллельных
прямых). Такие векторы называют
коллинеарными.
Нулевой
вектор считается коллинеарным любому
другому вектору. Коллинеарные векторы
![]() и
и
![]() связаны
соотношением
связаны
соотношением
![]() .
.
Векторы, лежащие в одной плоскости (или в параллельных плоскостях), называют компланарными.
Легко убедиться, что линейные операции удовлетворяют следующим свойствам:
1)
![]() ,
,
2)
![]() ,
,
3)
![]() .
.
Рассмотрим систему векторов
![]() . (1)
. (1)
Вектор
![]() где
где
![]() -
числа, называют линейной
комбинацией
векторов
-
числа, называют линейной
комбинацией
векторов
![]()
Определение.
Если существуют числа
![]() не все равные нулю такие, что линейная
комбинация векторов
не все равные нулю такие, что линейная
комбинация векторов
![]() обращается в нуль, то система векторов
(1) называется линейно
зависимой.
Если линейная комбинация обращается в
нуль только при
обращается в нуль, то система векторов
(1) называется линейно
зависимой.
Если линейная комбинация обращается в
нуль только при
![]() =
0, то –
линейно
независимой.
=
0, то –
линейно
независимой.
Заметим, что если среди векторов системы (1) есть хотя бы один нулевой вектор, то она будет линейно зависимой. Если среди векторов есть хотя бы два линейно зависимых, то и вся система будет линейно зависимой.
Теорема 1. Три компланарных геометрических вектора линейно зависимы.
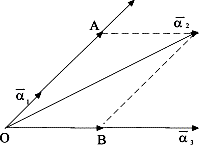
![]() лежат в одной плоскости и исходят из
одной точки. Используя правило сложения
векторов, получим
лежат в одной плоскости и исходят из
одной точки. Используя правило сложения
векторов, получим
![]() Поскольку векторы
Поскольку векторы
![]() и
и
![]() коллинеарны векторам
коллинеарны векторам
![]() и
и
![]() ,
то
,
то
![]()
![]() Тогда,
Тогда,
![]() или
или
![]() Последнее
равенство и означает линейную зависимость
векторов
Последнее
равенство и означает линейную зависимость
векторов
![]() .
Теорема доказана.
.
Теорема доказана.
Теорема 2. Три некомпланарных вектора линейно независимы.
Доказательство
от противного. Пусть векторы
![]() линейно
зависимы. Перепишем условие линейной
зависимости
линейно
зависимы. Перепишем условие линейной
зависимости
![]() иначе:
иначе:
![]() . (2)
. (2)
Из
(2) следует, что все три вектора
![]() лежат в одной плоскости, т.е. компланарны,
что противоречит условию теоремы. Это
противоречие и доказывает теорему.
лежат в одной плоскости, т.е. компланарны,
что противоречит условию теоремы. Это
противоречие и доказывает теорему.
Аналогично можно доказать, что два геометрических вектора линейно зависимы только тогда, когда они коллинеарны.
Теорема 3. Любые четыре геометрических вектора линейно зависимы.

![]() линейно зависимы, то и все четыре также
линейно зависимые.
линейно зависимы, то и все четыре также
линейно зависимые.
Поэтому
предположим, что
![]() линейно
независимые, а, следовательно, они не
компланарные.
линейно
независимые, а, следовательно, они не
компланарные.
Пусть
все векторы исходят из одной точки O.
Проведем через точку A (конец вектора
![]() )
прямую,
параллельную
вектору
)
прямую,
параллельную
вектору
![]() до пересечения с
плоскостью,
в которой лежат векторы
до пересечения с
плоскостью,
в которой лежат векторы
![]() и
и
![]() в
точке B. Через точку B проведем линию,
параллельную вектору
в
точке B. Через точку B проведем линию,
параллельную вектору
![]() до пересечения в точке D. Тогда согласно
правилу сложения векторов имеем
до пересечения в точке D. Тогда согласно
правилу сложения векторов имеем
![]() .
.
Последнее равенство и означает линейную зависимость четырех векторов. Теорема доказана.
Любая
упорядоченная некомпланарная (линейно
независимая) тройка геометрических
векторов
![]() называется базисом
в пространстве.
называется базисом
в пространстве.
Векторы
![]() называются базисными.
называются базисными.
Если
базисные векторы взаимно перпендикулярны,
то базис называется ортогональным.
Единичные векторы
![]() называются
ортами.
Базис называется ортонормированным,
если базисные векторы единичные и
взаимно перпендикулярные.
называются
ортами.
Базис называется ортонормированным,
если базисные векторы единичные и
взаимно перпендикулярные.
Совокупность
точки и базиса называют декартовой
системой координат.
Орты прямоугольной декартовой системы
координат обычно обозначают
![]()
Пусть
![]() некоторый базис. Присоединим к базисным
векторам четвертый вектор
некоторый базис. Присоединим к базисным
векторам четвертый вектор
![]() Поскольку всякая четверка векторов
линейно зависима, т.е.
Поскольку всякая четверка векторов
линейно зависима, т.е.
![]() то
то
![]()
![]() . (3)
. (3)
Формула
(3) дает разложение вектора
![]() по базису
по базису
![]() .
Коэффициенты
.
Коэффициенты
![]() называются координатами
вектора
называются координатами
вектора
![]() в этом базисе.
в этом базисе.
Можно
убедиться, что разложение вектора по
базису единственное. Последнее означает,
что координаты вектора однозначно
определяют сам вектор. Иначе говоря,
упорядоченную тройку чисел
![]() можно считать вектором в фиксированном
базисе.
можно считать вектором в фиксированном
базисе.
Очевидно, в множестве компланарных векторов любые два неколлинеарных вектора образуют базис, а всякий третий можно разложить по этому базису. В множестве коллинеарных векторов линейно независимый вектор один, он и образует базис в этом множестве.
Пример.
Являются ли векторы
![]() линейно зависимыми?
линейно зависимыми?
![]()
![]()
Решение.
Составим линейную комбинацию и приравняем
ее нулю
![]() ,
где
,
где
![]() – нуль вектор.
– нуль вектор.
Если
все
![]() то система линейно независимая. Используя
правила умножения вектора на число,
сложение и сравнение векторов, заданных
своими координатами, получим следующую
систему линейных уравнений
то система линейно независимая. Используя
правила умножения вектора на число,
сложение и сравнение векторов, заданных
своими координатами, получим следующую
систему линейных уравнений
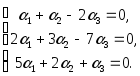
Заметим,
что формулы Крамера, полученные нами в
§3 для системы двух уравнений, справедливы
и для любой линейной системы n уравнений
с n неизвестными. Если определитель
системы
![]() то система имеет единственное решение,
определяемое формулами Крамера
то система имеет единственное решение,
определяемое формулами Крамера
![]()
Вычислим определитель нашей системы

Определители
![]() – равны нулю, т.к. имеют нулевые столбцы,
поэтому система имеет только нулевое
решение
– равны нулю, т.к. имеют нулевые столбцы,
поэтому система имеет только нулевое
решение
![]() Следовательно данные векторы линейно
независимые.
Следовательно данные векторы линейно
независимые.
Упражнение.
Взять данные векторы
![]() и
и
![]() за базис и разложить вектор
за базис и разложить вектор
![]() по этому базису.
по этому базису.
Ответ:
![]()
