
386 Broadband Microstrip Antennas
and |
|
F1 = 6 + (2p − 6) exp [−(30.666h /W )0.7528 ] |
(B.23) |
The frequency-dependent formula of the characteristic impedance of the microstrip line is given here [3].
|
|
Z 0 ( f ) = Z L (R 13 /R 14 )R17 |
|
|
(B.24) |
|||||||
where |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R 1 = 0.03891er1.4 |
|
|
(B.25) |
|||||||
|
|
R 2 = 0.267 (W /h )7.0 |
|
|
(B.26) |
|||||||
|
|
R 3 = 4.766 exp [−3.228 (W /h )0.641 ] |
|
(B.27) |
||||||||
|
|
R 4 = 0.016 + (0.0514er )4.524 |
|
|
(B.28) |
|||||||
|
|
R 5 = (hf /28.843)12 |
|
|
(B.29) |
|||||||
|
|
R 6 = 22.20 (W /h )1.92 |
|
|
(B.30) |
|||||||
R 7 = 1.206 − 0.3144 exp (−R 1) [1 − exp (−R 2)] |
(B.31) |
|||||||||||
R 8 = 1 + 1.275 [1 − exp {−0.004625R 3 er1.674 (hf /18.365)2.745 }] |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
(B.32) |
|
R 9 = 5.086R |
4 |
R 5 |
|
? |
exp (−R 6 ) |
? |
(er − 1)6 |
|
|
|||
0.3838 + 0.386R 4 |
1 + 1.2992R 5 |
|
1 + 10 (er − 1)6 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
(B.33) |
|
|
|
R 10 = 0.00044er2.136 + 0.0184 |
|
|
(B.34) |
|||||||
|
|
R 11 = |
|
(hf /19.47)6 |
|
|
|
(B.35) |
||||
|
|
|
+ 0.0962 (hf /19.47)6 |
|
|
|||||||
|
1 |
|
|
|
|
|||||||
Appendix B |
387 |
R 12 = 1/[1 + 0.00245 (W /h )2 ] |
(B.36) |
R 13 = 0.9408eeR8 − 0.9603 |
(B.37) |
R 14 = (0.9408 − R 9 )eeR8 − 0.9603 |
(B.38) |
R 15 = 0.707R 10 (hf /12.3)1.097 |
(B.39) |
R 16 = 1 + 0.0503er2R 11 [1 − exp {−(W /h )/15}6 ] |
(B.40) |
R 17 = R 7 [1 − 1.1241 (R 12 /R 16 ) exp {−0.026 (hf )1.15656 − R 15 }] (B.41)
B.3 Extension Due to Fringing Field
The extension DL in the length of the patch dimension to account for the fringing fields is given by [1, 2]:
DL = hj1 j 3 j5 /j4 |
(B.42) |
where
|
|
|
|
ee0.81 + 0.26 |
(W /h )0.8544 |
+ 0.236 |
||||||
j 1 |
= 0.434907 |
|
|
|
|
|
|
|
|
(B.43) |
||
ee0.81 − 0.189 |
|
(W /h )0.8544 |
+ |
0.87 |
||||||||
|
|
|
|
|
|
|||||||
|
|
|
j 2 = 1 + |
(W /h )0.371 |
|
|
|
|
(B.44) |
|||
|
|
|
2.358er + 1 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
||||
|
|
= 1 + |
0.5274 arctan [0.084 (W /h )1.9413/j2 ] |
|||||||||
|
j3 |
|
|
|
|
|
|
|
|
|
(B.45) |
|
|
|
|
ee0.9236 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
||||
j 4 = 1 + 0.0377 arctan [0.067 (W /h )1.456 ] {6 − 5 exp [0.036 (1 − er )]}
|
(B.46) |
j 5 = 1 − 0.218 exp (−7.5W /h ) |
(B.47) |

388 |
Broadband Microstrip Antennas |
The extension in the patch dimensions reduces with an increase in frequency. The dispersion effect of the fringing fields DL ( f ) is accounted by replacing ee by ee ( f ).
B.4 Attenuation Constant
The total attenuation constant a—to account for dielectric and conductor losses in a microstrip configuration—is given by [3]:
a = ad + acs + acg |
(B.48) |
where
ad = dielectric losses in the substrate
acs = conductor losses in the strip conductor acg = conductor losses in the ground plane
Various attenuation constants are given by
|
|
|
|
|
er |
ee ( f ) − 1 |
|||||||||
|
ad = 0.5b |
|
|
|
|
|
|
|
|
|
tan d |
||||
|
er − 1 |
ee ( f ) |
|
||||||||||||
|
|
|
|
|
|
|
|||||||||
|
|
|
|
acs = an R ss FDs Fs |
|
|
|||||||||
|
|
|
|
acg = an R sg FDg |
|
|
|||||||||
|
|
|
|
R ss = √ |
|
|
|
|
|
|
|||||
|
|
|
pfm 0 /ss |
|
|
||||||||||
|
|
|
|
R sg = √ |
|
|
|
|
|
||||||
|
|
|
p fm0 /sg |
|
|
||||||||||
a n = |
1 |
|
32 − (W ′/h )2 |
for W ′/h < 1 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
4phZ 0 |
S32 + (W ′/h )2 D |
||||||||||||||
|
|
|
|||||||||||||
(B.49)
(B.50)
(B.51)
(B.52)
(B.53)
(B.54)
|
ee |
|
|
0.667W ′/h |
|
|
|
||
a n = |
√ |
|
|
(W ′/h ) + |
for W ′/h ≥ 1 |
||||
2h 0 We |
F |
(W ′/h ) + 1.444 G |
|||||||
|
|
|
|
||||||
|
|
|
|
|
|
|
|
(B.55) |
|
|
FDs |
= 1 + (2/p ) arctan [1.4 (R ss Ds ss )2 ] |
(B.56) |
||||||
|
Appendix B |
|
|
389 |
||||
FDg = 1 + (2/p ) arctan [1.4 (R sg Dg sg )2 ] |
(B.57) |
|||||||
|
W ′ S |
|
p |
t |
D |
|
||
Fs = 1 + |
2h |
|
1 − |
1 |
+ |
W ′ − W |
|
(B.58) |
|
|
|
|
|||||
where Ds and Dg are the rms surface error of the patch conductor and the ground plane, respectively. The as and ag are the conductivity of patch conductor and ground plane, respectively. Copper is the most commonly used conductor in the substrate. Its conductivity as = ag = 5.6 × 107 mho/cm.
References
[1]James, J. R., and P. S. Hall, Handbook of Microstrip Antennas, Vol. 1, London: Peter Peregrinus, Ltd., 1989.
[2]Ray, K. P., and G. Kumar, ‘‘Determination of the Resonant Frequency of Microstrip Antennas,’’ Microwave Optical Tech. Letters, Vol. 23, October 1999, pp. 114–117.
[3]Hoffmann, R. K., Handbook of Microwave Integrated Circuits, Norwood, MA: Artech House, 1987.
Appendix C:
MNM for RMSAs
C.1 Introduction
In the MNM for analyzing MSAs, electromagnetic fields underneath the patch and outside the patch are modeled separately [1]. The fields underneath the patch are modeled using Green’s function approach. The patch is analyzed as a two-dimensional planar network. The dimensions of the patch are extended outward to account for the fringing fields. Multiple numbers of ports are located along the extended periphery. The length of each port should be small so that the field over this length is uniform. The number of ports depends on the field distribution along the edge. A greater number of ports should be chosen when there is a larger variation in the field distribution. Green’s function for the rectangle is given in Section C.2.
The fields outside the patch, namely the fringing fields along the edges and the radiation fields, are incorporated by adding equivalent edge admittance networks (EANs), as described in Section C.4. The impedance matrixes corresponding to the patch and the fringing fields are combined using the segmentation method to obtain the input impedance and voltage distribution around the periphery of the patch. The radiation pattern is obtained from the voltage distribution along the periphery of the antenna [1–4].
C.2 Green’s Function for RMSAs
For a planar rectangular cavity having a perfect magnetic wall along its periphery, the mode vector C is obtained from the solution of the wave equation:
391
392 |
Broadband Microstrip Antennas |
|
|
X=2T + k 2 CC = 0 |
(C.1) |
|
The solution of C is given by |
|
C = [A sin (mp x /L ) + B cos (mp x /L )] [C sin (np y /W ) + D cos (npy /W )] (C.2)
where k is the propagation constant, also known as wave number, and is equal to 2p/l.
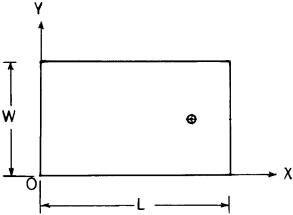
Here, L and W are the length and the width of the rectangular patch along the x and y directions as shown in Figure C.1, and m and n represent the modal indexes. The constants A, B, C, and D are obtained by applying the boundary condition: dC/dn = 0, where n represents the outward normal to the boundary.
The mode vector Cmn for the mn th mode is given by |
|
Cmn = cos (mpx /L ) cos (np y /W ) |
(C.3) |
The wave equation for a z -directed electric current source at a point (x 0, y 0) is given by
X=T2 + k 2 CG (x , y /x 0, y 0 ) = d(x − x 0, y − y 0 ) |
(C.4) |
where G (x , y /x 0, y 0 ) is Green’s function |
of the given geometry and d is |
the delta function. Green’s function of an |
RMSA is given by [1, 5] |
Figure C.1 RMSA.

394 Broadband Microstrip Antennas
where (x i , y i ) and (x j , y j ) denote the locations of the two ports of widths Wi and Wj , respectively.
The integral in (C.10) yields
|
jvm h |
∞ ∞ |
|
Z ij = |
∑ ∑ G (x i , y i /x j , y j ) sin c (k x Wi /2) sin c (k y Wj /2) |
||
LW |
|||
|
m = 0 n = 0 |
||
|
|
||
|
|
(C.11) |
Once the Z -matrix corresponding to all the ports is obtained, then the input impedance is calculated using segmentation method.
C.3 Effective Loss Tangent and Power Losses
The radiated power from the MSA is modeled by the EAN. The dielectric loss in the dielectric material of the substrate and the conductor losses in the patch and ground plane are taken into account by modifying the loss tangent tan d of the substrate to the effective loss tangent tan de . Consequently, tan de is greater than tan d as it accounts for both dielectric and conductor losses.
tan d e = |
Pd + Pc |
tan d |
(C.12) |
|
Pd |
||||
|
|
|
where Pd is the power loss due to dissipation in the dielectric and Pc is the power loss in the conductor; they are given by [1, 6]:
Pd = h |
E |
sd | E |2 ds |
(C.13) |
|
|||
|
S |
|
|
Pc = 2 |
E |
R s | H |2 ds |
(C.14) |
|
S
where E and H are the electric and magnetic fields, respectively. R s is the skin-effect surface resistance of the conductor with conductivity sc and is given by
R s = √ |
2p fm /sc |
(C.15) |
Appendix C |
395 |
and
sd = ve0 er tan d |
(C.16) |
C.4 EAN
In MNM, the EAN represents the fields external to the patch, namely the fringing and radiated fields. If the physical dimensions of the patch are taken, then the EAN consists of parallel combinations of capacitance C and conductance G. The capacitance represents the energy stored in the fringing fields and the conductance G includes the radiation conductance corresponding to the radiated power, the surface wave conductance, and the mutual conductance.
Instead of loading with capacitance, edge extensions can be added to the physical dimensions of the patch, which accounts for the fringing fields. This approach of extending the edge is preferred because then EAN consists of only conductance G. The expressions for the edge extension, which takes into account the dispersion effect, are given in Appendix B.
The radiation conductance associated with an edge of the microstrip patch is defined as conductance, which will dissipate power equal to that radiated by the edge. If the edge is of width W and the power radiated for uniform voltage distribution is Prad, then the radiation conductance per unit length of the edge is given by Gr = 2Prad /W. The closed-form expression for radiation conductance Gr is given by [7]
Gr = |
w |
2 |
(C.17) |
6p2(60 |
|
||
|
+ w 2 ) |
||
where
w = k 0We
k 0 = 2p /l0
Here, We = W + DW. The value of DW is obtained by using the edge extension formula given in Appendix B and l0 is the free-space wavelength. For n uniformly spaced ports along the edge, the radiation conductance connected to each port is chosen to be Gr /n .
The surface-wave conductance Gs is given by [1]:
