
- •2.3.2. Джиттер
- •2.4. Математическая модель канала с замираниями
- •3.4. Избыточность источника
- •3.6. Совместная энтропия двух источников
- •3.7. Скорость передачи и пропускная способность канала связи
- •4.1.2. Представление аналоговых сигналов в дискретной форме
- •4.1.4. Дискретизация полосовых сигналов
- •4.1.5. Дискретизация сигналов в реальных системах
- •4.1.7. Выводы и практические рекомендации
- •4.2. Квантование по уровню
- •4.2.3. Техническая реализация схем квантования по уровню
- •5.4. Алгоритм Лемпеля−Зива−Велча (LZW)
- •6.1. Симметричные криптосистемы
- •6.3. Криптографический протокол

4.2.2. Величина шума квантования
Квантователь определяет некоторый сигнал ошибки (см. сигнал e(t)
на рис. 4.5). Пиковое значение ошибки декодирования |
|
|||||
P |
1 |
|
1 |
, |
(4.24) |
|
2M |
2n 1 |
|||||
|
|
|
|
|||
где n – количество разрядов кодового слова.
Следовательно, для того чтобы пиковое значение не превышало P ,
цифрового преобразователя (АЦП) и при необходимости преобразователя
необходимо обеспечить разрядность кода n из условия: |
|
|
|
||||||
n log |
1 |
1 log P 1 |
3,322lg P 1 . |
|
|
(4.25) |
|||
|
|
|
|||||||
|
P |
|
|
|
|
|
Р |
||
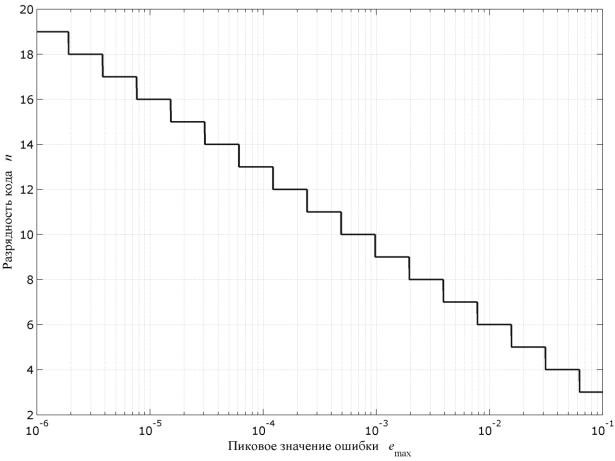
График функции для целых n представлен на рис. 4.11. |
|||||||||
|
|
||||||||
По приведѐнному графику можно определить минимально допустимую |
|||||||||
|
|
|
|
|
|
И |
|
||
разрядность последовательного кода, обеспечивающую заданное пиковое |
|||||||||
значение ошибки. |
|
|
|
У |
|
|
|||
|
|
|
|
|
|
|
|||
|
|
|
|
Г |
|
|
|
||
4.2.3. Техническая реализация схем квантования по уровню |
|
||||||||
|
|
|
|
Б |
|
|
|
|
|
Схемы формирования цифрового сигнала состоят из аналого- |
|||||||||
|
|
а |
|
|
|
|
|||
|
|
к |
|
|
|
|
|
||
параллельного кода в последоват льный. Современные АЦП строятся по |
|
Все иные т пы АЦПявляются либо модификациями, либо комбинаци- |
|
трѐм базовым схемам: |
|
– схемы с последова ельнымесчѐтом; |
|
– схемы на основе последова ельного приближения; |
|
– схемы параллельн |
кодирования. |
и |
|
л |
|
ями указанных трѐх. го В момент взят я выборки в кодере с последовательным счѐтом одно-
временнобс двоичным счѐтчиком запускается генератор линейно нарастающегоинапряжения (ГЛИН). Когда значение линейно нарастающего напряже- н я станов тся равным значению выборки кодируемого сигнала, с двоичного Бсчѐтч ка осуществляется съѐм данных в виде двоичного числа заданной разрядности. После этого происходит сброс счѐтчика и ГЛИН в состояние «нуль». Процедура повторяется в течение каждого интервала дискретизации
T . Подход отличается простотой, требует минимума элементов, однако скорость преобразования сравнительно невысока, т. к. она определяется скоростью переключения состояний счѐтчика.
Кодер с последовательным приближением, или поиском, работает по принципу сравнения значений выборок с некоторыми пробными уровнями напряжения. Следующее пробное напряжение зависит от результата предыдущего, а интервал поиска уменьшается в два раза. В связи с тем, что поиск
66
начинается в середине области допустимых значений кодируемого сигнала, т. е. является грубым, а потом всѐ уточняется, результат достигается сравнительно быстро. Опорные уровни формируются последовательностью делителей напряжения, коммутируемых друг с другом электронными ключами. Коммутация осуществляется логическими схемами аппаратно. После того, как значение выборки не будет отличаться от сформированного опорного напряжения более, чем на половину кванта, осуществляется съѐм кода, или числа, кодирующего значение выборки. Подход требует большего числа прецизионных компонентов, таких как высокостабильные делители напряжения,
однако скорость кодирования на порядок выше, чем у кодера с последова- |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
Р |
тельным счѐтом, и определяется она скоростью работы коммутаторов. |
|||||||||||
|
|
|
|
|
|
|
|
|
|
И |
|
|
|
|
|
|
|
|
|
|
У |
|
|
|
|
|
|
|
|
|
|
Г |
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
|
|
|
|
к |
|
|
|
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
и |
л |
|
|
|
|
|
|
|
|
|
|
Рис. 4.11. Зав симость минимальной длины кодового слова для заданной ве- |
|||||||||||
Б |
бличины ошибки декодирования цифрового сигнала |
|
|||||||||
|
|
||||||||||
Параллельные кодеры включают в себя множество параллельно включѐнных компараторов, каждый из которых осуществляет сравнение выборки с одним конкретным значением опорного напряжения. Последовательность выборок подаѐтся одновременно на все компараторы. Множество высоких и низких уровней на выходе компараторов после процедуры двоичного преобразования (шифрации) определяет значение кодового слова ИКМ-сигнала. Подход отличается наивысшей скоростью преобразования, однако схемно наиболее громоздок.
67
4.2.4. Шумовые эффекты в цифровых системах
Результат декодирования цифрового сигнала представляет собой аддитивную смесь аналогового сигнала и шума. Возникновение шумовых искажений на выходе декодера обусловлено двумя факторами:
1) шумами квантования; 2) ошибками в символах цифрового сигнала (битовые ошибки).
Битовые ошибки возникают из-за помех в канале передачи информации и неравномерности амплитудно-частотной характеристики (АЧХ) канала в пределах полосы частот, занимаемой цифровым сигналом. При недостаточной фильтрации аналогового сигнала на входе кодера могут возникать дополнительные искажения за счѐт перекрытия фрагментов спектра дискретного сигнала.
|
При определѐнных условиях отношение средней мощности аналогово- |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Р |
|
го сигнала к средней мощности шума на выходе декодера определяется вы- |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
И |
|
|
ражением |
|
|
|
|
|
|
|
|
У |
|
|
||
|
|
q |
|
|
|
M 2 |
, |
|
|
(4.26) |
|||
|
|
1 4(M 2 |
1)P |
|
|
||||||||
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
e |
|
Г |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
где Pe – вероятность появления ошибочного символа цифрового кода. |
|
||||||||||||
|
Как видно из (4.26), при отсутствии ошибок в цифровом сигнале каче- |
||||||||||||
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
ство декодирования определяется лишь количеством уровней квантования: |
|||||||||||||
|
|
|
|
qmax |
|
а2 |
|
|
|
|
(4.27) |
||
|
|
|
|
M . |
|
|
|
|
|
||||
|
|
|
|
|
к |
|
|
|
|
|
|
||
|
С практической очки |
|
|
|
шумы квантования в зависимости от |
||||||||
|
|
|
зрения |
|
|
|
|
|
|
|
|||
условий работы декодера можно разделить на четыре группы: |
|
|
|||||||||||
|
1) шумы перегруз к; |
|
|
|
|
|
|
|
|
|
|
|
|
|
2) случайные шумы; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
||
|
3) гранулярные шумы; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
4) шумы покоя. |
|
|
|
|
|
|
|
|
|
|
|
|
|
Случайныеишумы определяются собственно эффектом квантования вы- |
||||||||||||
борок |
а и наб юдаются при нормальном режиме работы квантователя, |
||||||||||||
|
л |
|
|
|
|
|
|
|
|
|
|
|
|
когда д нам ческий диапазон аналогового сигнала и амплитудная характе- |
|||||||||||||
рист ка квантователя согласованы. |
|
|
|
|
|
|
|
|
|
||||
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
В случае если динамический диапазон сигнала сравним с величиной |
||||||||||||
квантасигна, наблюдается так называемый гранулярный шум. На выходе декодера |
|||||||||||||
Бнаблюдается значительное ухудшение сигнал−шум, а аналоговый сигнал существенно огрубляется.
Шум покоя наблюдается при постоянных или медленно изменяющихся кодируемых сигналах. В этом случае на выходе декодера возникает некото-
рая осциллирующая с частотой fд 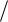 2 составляющая. Шум покоя можно исключить путѐм режекции аналоговым фильтром спектральной компоненты
2 составляющая. Шум покоя можно исключить путѐм режекции аналоговым фильтром спектральной компоненты
68
на частоте fд 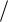 2 или исключением возможности переходов по уровню для неизменяющихся величин.
2 или исключением возможности переходов по уровню для неизменяющихся величин.
Если сигнал на входе кодера равен нулю, такой режим работы называется режимом простоя и в этом случае шум покоя можно исключить введением в амплитудную характеристику квантователя так называемой «мѐртвой зоны» – горизонтальной ступеньки при малых входных напряжениях, в отличие от вертикальной ступеньки, как это показано на рис. 4.11.
Учитывая, что M 2n , выражение для отношения С/Ш можно записать
в следующем виде: |
|
q[дБ] 6,02n α . |
(4.28) |
|
Р |
где – число, зависящее от структуры кода , формы элементарного символа, |
|
динамического диапазона и закона распределения мгновенных значений ана- |
||
|
|
И |
логового сигнала. Для цифровых символов прямоугольной формы и равно- |
||
мерного закона распределения аналогового сигнала 0. |
|
|
|
У |
|
Из полученного выражения видно, что увеличение длины кода на один |
||
Г |
|
|
Б |
|
|
разряд увеличивает предельное отношение С/Ш приблизительно на 6 дБ. Так, |
||
для обеспечения отношения С/Ш на выходе декодера не хуже 96 дБ длину кода необходимо выбрать как минимум р вной 16. Тогда полоса частот ИКМ-сигнала, определяемая первым нулѐм в спектре, будет в 32 раза шире
полосы частот, занимаемой аналоговым |
сигналом |
. |
||||
|
|
|
к |
|
||
4.2.5. Неравномерное кван |
|
|
сигналов |
|||
|
|
ование |
|
|
||
Некоторые |
|
, например речевые, имеют плотность вероятности |
||||
|
|
т |
|
|
|
|
распределения мгновенных значений с максимумом вблизи нуля. Это значит, |
||||||
что наиболее вероятнымиоявляются не пиковые значения напряжений, а |
||||||
|
сигналы |
|
|
|
|
|
л |
|
|
|
|
|
|
напряжения, имеющ е малый уровень. Для таких сигналов с неравномерным распределениембмгновенных значений гранулярный шум квантования является превалирующими с точки зрения качества систем передачи информации.
В целях адаптации к такого рода сигналам широко используется неравномерноеБквантование выборок сигнала, подразумевающее уменьшение шага квантования для значений вблизи нуля.
Неравномерное квантование может быть осуществлено путѐм предварительного компандирования сигнала с последующей его подачей на обычный цифровой кодер. В результате компандирования происходит перераспределение мгновенных значений сигнала согласно некоторому закону. В Северной Америке и Японии в качестве компандирующих используются безынерционные нелинейные преобразователи, в которых амплитудная характеристика подчиняется -закону. В Европе применяется аналогичная ха-
69
рактеристика, подчиняющаяся несколько иному A - закону. Прямое компандирование называется компрессией, обратное – экспандированием.
Характеристика -типа определена следующим образом:
y(t) sign x(t) |
ln(1 | x(t) |) |
, |
(4.29) |
|
ln(1 ) |
||||
|
|
|
где x(t) ( 1;1) и y(t) ( 1;1) – входной компрессируемый и выходной процесс соответственно; – константа, определяющая степень сжатия динами-
ческого диапазона сигнала. |
|
|
|
|
|
|
|
|
|
|
|
|
|
Р |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
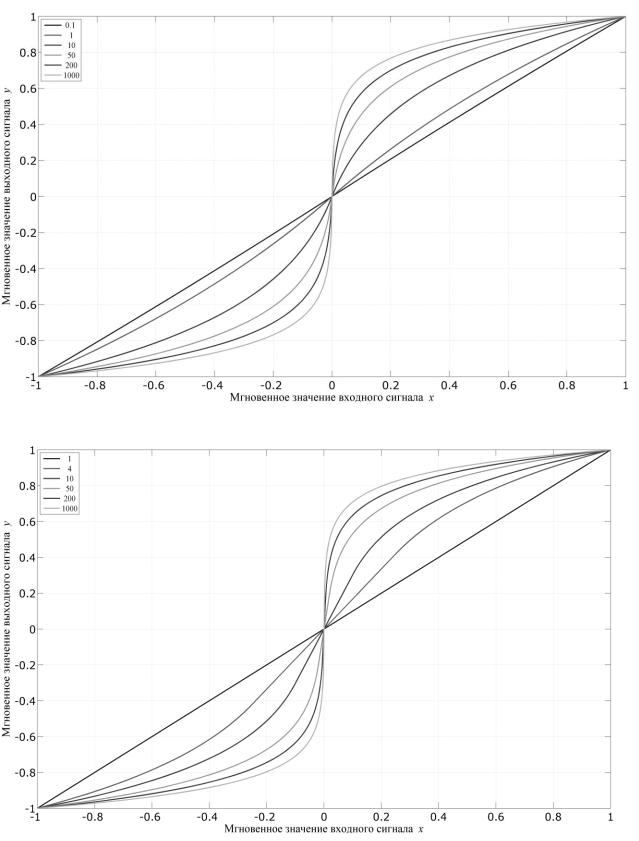
Семейство графиков зависимости (4.29) при различных значениях па- |
|||||||||||||||||||
раметра μ представлено на рис. 4.12. |
|
|
|
|
|
|
|
|
|
И |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Характеристика A -типа описывается следующей функциональной за- |
|||||||||||||||||||
висимостью: |
|
|
|
|
|
|
|
|
|
|
|
|
У |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
sign x(t) |
A | x(t) | |
, | x(t) | 0; |
1 |
; |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
||
|
|
|
|
|
|
1 ln A |
|
|
|
|
A |
|
|
|
|
|
|||
|
|
y(t) |
|
|
1 ln A | x(t) | |
|
|
Г |
|
|
(4.30) |
||||||||
|
|
|
|
|
x(t) |
|
|
|
а |
|
|
1 |
|
|
|
||||
|
|
|
sign |
1 ln A |
|
, |
| x(t) | |
|
;1 , |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|||||
|
|
|
|
|
|
|
к |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
|
|
|
||
где A 1 – параметр нелинейной фун ции преобразования. |
|
|
|||||||||||||||||
Семейство графиков зависимости (4.30) при различных значениях па- |
|||||||||||||||||||
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
раметра |
A представлено на рис. 4.13. |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
л |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
70
|
|
|
|
|
|
|
|
|
|
|
|
Р |
|
|
|
|
|
|
|
|
|
|
|
И |
|
|
|
|
|
|
|
|
|
|
|
У |
|
|
|
|
|
|
|
|
|
|
|
Г |
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
Рис. 4.12. Нелинейная характеристика μ -типа |
|
|
||||||||
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
|
|
|
|
|
к |
|
|
|
|
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
л |
|
|
|
|
|
|
|
|
|
|
|
б |
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 4.13. Нелинейная характеристика A -типа
71
4.2.6. Дифференциальное квантование
Дифференциальное квантование имеет место, когда квантованию подвергаются не сами импульсы, а разница их амплитуд. Схема кодирования может изменять диапазон возможных значений, если разница между значениями амплитуд выходит за границы текущего диапазона возможных значений. В этом случае говорят об адаптивном дифференциальном квантовании. Такой подход позволяет учесть все возможные разницы амплитуд, но может привести к увеличению погрешности квантования.
Для успешного восстановления формы аналогового сигнала принимающей стороной достаточно информации об относительном изменении амплитуды двух соседних импульсов. Поэтому для реализации метода, называемого дельта-модуляцией, требуется только один бит, указывающий на
направление изменения амплитуды. |
|
Р |
|
|
|
При дельта-модуляции каждому биту соответствует целое значение |
||
|
И |
|
|
У |
|
амплитуды. В результате при передаче каждого значения амплитуды переда- |
||
ется относительно небольшое количество информации об этом значении, что |
||
зультат. Единственный способ, позволяющий удерживатьГ оба типа искажений в допустимых пределах, − применение достаточно малого шага дискре-
тизации. Соответственно, такой способ предполагаетБиспользование частоты дискретизации, превышающей частоту Н йквиста. Для каждого значения ам-
является основной причиной, по которой зернистость может изменить ре-
перед ней задачи. Однако э о под силу другой методике, основанной на дель-
плитуды отводится 1 бит, поэтому битов я скорость соответствует скорости |
||
|
а |
|
дискретизации. Этот метод разработан, чтобы сократить расход полосы про- |
||
пускания, но не следует ради н го отказыватьсяк |
от преимуществ сжатия. |
|
Дельта-модуляция не вс гда мож т эффективно решить поставленные |
||
е |
|
|
т |
|
|
та-модуляции. Она называебо ся дельта-модуляцией с переменной крутизной наклона (CVSDMпониженияContinuously Variable Slope Delta Modulation). Метод
CVSDM позволяет наблюдать за управлением битовым потоком. Для этого можно испо ьзовать л последовательность единиц, увеличивающую размер шага д я наклона аналогового сигнала, либо последователь-
модуляц просто выполняется наблюдение за тенденциями посредством за- Бпом нан я предыдущих направлений изменения амплитуды. Если для мно-
ность нулейб,луменьшающую размер шага для увеличения крутизны наклона и ослабленияимпульсовэффекта зернистости. В других адаптивных формах дельтагих было замечено одно и то же направление изменения амплиту-
ды, то можно предположить, что наклон сигнала является достаточно пологим. Чтобы уменьшить зернистость, нужно уменьшить шаг дискретизации. И наоборот, если чередуются отрицательные и положительные направления изменения амплитуды, это говорит о том, что наклон получился выше нормы. В этом случае шаг дискретизации увеличивается во избежание завышения наклона кривой.
В дополнение к временным методам, существуют и частотные методы кодирования источника информации. Они имеют ряд преимуществ. При ис-
72
пользовании, например SB-ADPCM, входной сигнал разбивается на несколько частотных полос, которые кодируются независимо друг от друга при помощи метода ADPCM. На принимающей стороне биты декодируются, в результате чего восстанавливается исходный полосовой сигнал.
Преимущество этого метода в том, что погрешность в каждом диапазоне частот зависит только от кодирования. Поэтому можно использовать более точные схемы кодирования и шаги квантования для тех диапазонов частот, которые наиболее важны для воспроизведения сигнала. Таким образом, погрешность в этих диапазонах частот невелика, в то время, как в других до-
пустим более высокий уровень погрешности. |
Р |
|
|
Между соседними отсчѐтами речевого сигнала имеется значительная |
|
корреляция, которая слабо убывает по мере увеличения интервала между отсчетами. Это означает, что речевой сигнал изменяется медленно и разность между соседними отсчетами будет иметь меньшую дисперсию, чем исходный сигнал, что позволяет применять методы разностного квантования рече-
вого сигнала. |
И |
|
|
Линейная дельта-модуляция использует одноразрядный (двухуровне- |
|
вый) квантователь и предсказатель. Восстановление аналогового сигнала из |
|
|
У |
сигнала линейной ДМ осуществляется суммированием шага квантования. |
|
Г |
|
Б |
|
Линейная дельта-модуляция технически реализуется относительно просто, но обладает рядом недостатков: перегрузка но крутизне; шум дробления (шум незанятого канала). Кроме того, для обеспечения приемлемого
качества восстановления речевого сигн |
требуется высокая скорость пре- |
||||||
|
|
|
|
|
|
е |
|
образования (передачи) порядка 200 битла/с. |
|||||||
В адаптивной дельта-модуляцикшаг квантования меняется в зависимо- |
|||||||
|
|
|
|
|
т |
|
|
сти от крутизны исходного сигнала от минимального до максимального зна- |
|||||||
чения. |
|
|
|
о |
|
|
|
|
|
|
|
|
|
||
|
|
|
и |
|
|
|
|
|
|
л |
|
|
|
|
|
|
б |
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
73
5.КОДИРОВАНИЕ ИСТОЧНИКА
5.1.Понятие префиксного кода
Префиксный код − это код со словом переменной длины, удовлетворяющий условию Фано (Роберт Фано 1917 г. р. − итало-американский учѐный, известный специалист по теории информации).
Условие Фано. Если кодовое слово a принадлежит некоторому непустому кодовому множеству, то кодового слова ab в данном множестве не существует. Формулировка означает, что никакое кодовое слово не может быть началом другого кодового слова. Таким образом, несмотря на то что префиксный код состоит из кодовых слов разной длины, эти слова можно записывать без разделительного символа.
Примером кода, удовлетворяющего условию Р. Фано, являются теле- |
|
|
Р |
фонные номера. Если в сети существует номер 101, то номер 1012345 не мо- |
|
И |
|
У |
|
жет быть выдан: при наборе трѐх цифр АТС прекращает «понимать» даль- |
|
нейший набор и соединяет с адресатом по номеру 101. Однако для набора с |
|
завершение последовательности знаков соответствующейБГ кнопкой. Таким образом, 101, 1010 и 1012345 идентифицируются системой как различные.
сотового телефона это правило уже не действует, потому что требуется явное
является, и то же сообщение можно тратовать несколькими способами:
Код, состоящий из слов «0», «10» и «11», является префиксным, и сообщение «01001101110» можно разбить на слова единственным образом:
к «0 10 0 11 0 11 10» или «0 100 11е0 11 10». Иными словами, каждый элемент
«0 10 0 11 0 11 10». Код, состоящий из слов 0, 10, 11 и 100, префиксным не
кодового множества является и кодовым словом, и префиксом, отделяющим кодовое слово от предыдущего и последующего кодового слова в информа-
ционном потоке. При ф рмировании кодового множества недопустимые
префиксы (кодовые сл ва) |
|
быть получены путѐм последовательного |
|
|
могут |
|
|
отбрасывания последнего знака определѐнной кодовой комбинации. Напри- |
|||
мер, для кодовой комбнации |
«11101101» префиксами будут «1110110», |
||
«111011», «11101», «1110», «111», «11», «1». |
|||
и |
|
|
|
Часть кодовой комбинации, дополняющая префикс до самой комбина- |
|||
ции, называетсялсуффиксом. Таким образом, множество кодовых слов может |
|||
ксами БПрефиксные коды наглядно представляются с помощью кодовых дере-
состоять л о из одних префиксов, либо из префиксов, объединѐнных с суф- |
|
ф |
б |
. |
|
вьев. Если ни один узел кодового дерева не является вершиной данного кода, то он обладает свойствами префикса. Узлы дерева, которые не соединяются с другими, называются конечными. Комбинации, которые им соответствуют, являются кодовыми комбинациями префиксного кода. Любой код со словом фиксированной длины, очевидно, является префиксным.
74
5.2.Неравенство Крафта
Пусть заданы два произвольных конечных множества, которые называются соответственно кодируемым алфавитом и кодирующим алфавитом. Их элементы называются символами, а строки, или последовательности конечной длины, символов − словами. Длина слова − это число символов, из которого оно состоит.
В качестве кодирующего алфавита часто рассматривается множество {0, 1} − двоичный алфавит.
Схемой алфавитного кодирования, или просто алфавитным кодом, называется любое отображение символов кодируемого алфавита в слова кодирующего алфавита, которые называют кодовыми словами. Пользуясь схемой кодирования, каждому слову кодируемого алфавита можно поставить
его код − конкатенацию кодовых слов, соответствующих каждому символу |
|||||
этого слова. |
|
|
|
|
Р |
|
|
|
|
|
|
Код называется разделимым, или однозначно декодируемым, если ни- |
|||||
|
|
|
|
И |
|
каким двум словам кодируемого алфавита не может быть поставлен в соот- |
|||||
ветствие один и тот же код. |
|
|
У |
|
|
|
|
|
|
||
Префиксным кодом называется алфавитный код, в котором ни одно из |
|||||
|
|
Г |
|
|
|
|
|
Б |
|
|
|
кодовых слов не является префиксом никакого другого кодового слова. Лю- |
|||||
бой префиксный код является разделимым. |
|
|
|
|
|
Теорема 5.1 |
а |
|
|
|
|
|
|
|
|
||
Пусть заданы кодируемый и одирующий алфавиты, состоящие из m и |
|||||
n символов соответственно и заданыкж лаемые длины кодовых слов: l1, l2 , |
|||||
..., lm . Тогда необходимым и дос а очным условием существования раздели- |
|||||
мого и префиксного |
|
|
е |
|
|
|
, обладающих заданным набором длин кодовых |
||||
слов, является выполнение неравенс ва |
|
||||
|
|
т |
|
|
|
|
кодов |
m |
|
|
|
|
n li |
1. |
(5.1) |
||
и |
|
i 1 |
|
|
|
|
|
|
|
||
Это неравенствол |
известно |
под названием |
неравенства Краф- |
||
та−Макмибллана. Впервые оно было выведено Леоном Крафтом в его магистерскойБд пломной работе в 1949 г., однако он рассматривал только префиксные коды, поэтому при обсуждении префиксных кодов это неравенство часто называют просто неравенством Крафта. В 1956 г. Броквей Макмиллан доказал необходимость и достаточность этого неравенства для более общего класса кодов ‒ разделимых кодов.
75
5.3.Алгоритм Хаффмана
В 1952 г. американский математик Дэвид Хаффман (1925−1999) предложил алгоритм формирования префиксного кода для компрессии без потерь (архивации).
Предположим, что нужно устранить информационную избыточность следующей символьной последовательности «AAABCCD». При условии кодирования одного символа восемью битами эта последовательность занимает 7 байт. Компрессия по методу кодирования повторов даст следующий результат: «3A1B2C1D», т. е. объѐм сообщения стал равен 8 байтам. Алгоритм Хаффмана позволяет сократить объѐм исходного сообщения до 2 байт за счѐт использования априорной информации о частоте появления той или иной буквы в сообщении.
Составим таблицу частот появления букв для нашего примера. Симво- |
||||||
|
|
|
|
|
|
Р |
лы «A», «B», «C», «D» появляются в сообщении 3, 1, 2 и 1 раз соответствен- |
||||||
|
|
|
|
|
И |
|
|
|
|
|
У |
|
|
но. Затем эти сведения используются для построения так называемого дво- |
||||||
|
|
|
Г |
|
|
|
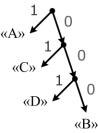
ичного дерева (рис. 5.1), используемого для генерации кодированной после- |
||||||
довательности. |
|
|
Б |
|
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
к |
|
|
|
|
|
|
е |
|
|
|
|
|
Левые ветви дерева тмечены кодом «0», а правые − «1». Слово, коди- |
||||||
|
Рис. 5.1. Кодовое дерево Хаффмана |
|
|
|||
|
о |
|
|
|
|
|
|
и |
|
|
|
|
|
рующее определѐнный с мв л, образуется при прохождении от вершины де- |
||||||
разл чной длины. Так как код Хаффмана является префиксным, то специаль- |
||||||
рева к симво у. Так м образом, буква «A» кодируется единицей, буква «C» − |
||||||
б |
|
|
|
|
|
|
последовате ьностью «01», D − последовательностью «001», а «B» − после-
довательностью «000», и различные символы кодируются кодовыми словами
Бчтоипоследовательность «1110000101001» кодирует текст «AAABBCCD» тринадцатью битами.
ного раздел теля между кодовыми словами не требуется. Отсюда следует,
Недостатки кода Хаффмана отмечены ниже.
1. Для последовательностей, представленных различными алфавитами и имеющими различную статистическую структуру, согласно методу необходимо генерировать различные двоичные деревья, что требует переформатирования дерева Хаффмана.
Например, в русскоязычных текстах чаще всего встречается буква «А», она будет стоять у вершины дерева и ей будет присвоен код, равный двоичной единице. В англоязычных текстах самая частая буква − «E», и единич-
76
