
- •2.3.2. Джиттер
- •2.4. Математическая модель канала с замираниями
- •3.4. Избыточность источника
- •3.6. Совместная энтропия двух источников
- •3.7. Скорость передачи и пропускная способность канала связи
- •4.1.2. Представление аналоговых сигналов в дискретной форме
- •4.1.4. Дискретизация полосовых сигналов
- •4.1.5. Дискретизация сигналов в реальных системах
- •4.1.7. Выводы и практические рекомендации
- •4.2. Квантование по уровню
- •4.2.3. Техническая реализация схем квантования по уровню
- •5.4. Алгоритм Лемпеля−Зива−Велча (LZW)
- •6.1. Симметричные криптосистемы
- •6.3. Криптографический протокол
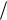
следовательности отсчѐтов. Сущность и практическую ценность теоремы В. А. Котельникова можно сформулировать двумя утверждениями:
– если сигнал имеет спектр, не содержащий значений выше некоторой частоты fm Гц, то такой сигнал в полной мере описывается своими значени-
ями – отсчѐтами, – взятыми через равные интервалы времени, не превышающие 1 2 fm с;
– сигнал может быть точно восстановлен по своим отсчѐтам, следующим друг за другом с частотой не менее 2 fm Гц.
Теорема Котельникова предполагает, что спектр сигнала строго огра-
большинства реально используемых сигналов вступает в противоречиеР с условием теоремы Котельникова. В связи с этим перед процессом дискрети-
ничен. Известно, что сигнал с конечным спектром имеет бесконечную дли-
тельность и, соответственно, сигнал с конечной длительностью имеет спектр
в бесконечно широкой полосе частот. Таким образом, конечная длительность
зации сигнала обязательно должна быть осуществлена процедура фильтра- |
|||
ции сигнала. |
|
|
И |
|
|
У |
|
|
|
Г |
|
4.2. Квантование по уровню |
|
Б |
|
|
|
|
|
|
а |
|
|
4.2.1. Место квантования сигнала в процедуре преобразования |
|||
к |
|
|
|
аналоговых сигналов в цифровые |
|
|
|
е |
|
|
|
Кодирование дискретного сигнала – |
это специальный тип аналого- |
||
цифрового преобразования, при котором значения дискретного сигнала в отсчѐтных точках кодирую ся последовательным двоичным кодом.
Полагается, что двоичный код состоит из последовательности слов
объѐмом |
n бит. |
Таким |
|
бразом, количество уникальных кодовых слов |
||
M 2n |
|
|
выборки |
т |
||
рок. |
. |
Каждое значен |
е к д вого слова соответствует некоторому извест- |
|||
|
интервалы называют квантами, а сам дискретный сигнал предва- |
|||||
ному значению |
|
ос гнала. Так как область допустимых значений вы- |
||||
борок представ яет собой континуум, то кодовые слова в действительности кодируютбне конкретные значения, а некоторые интервалы значений выбо-
рительноТакиеподвергается квантованию. В результате квантования формируется дискретныйБ с гнал, в котором значения выборок приравнены ближайшим разрешѐнным значениям – уровням квантования. Количество таких разрешѐнных значений не должно превышать объѐма M кодовых слов.
Преобразование аналогового сигнала в цифровой предполагает осуществление трѐх основных операций: дискретизации, квантования и собственно кодирования (см. рис. 4.4).
61
Операция дискретизации формирует последовательность равноотстояР - щих друг от друга плосковершинных прямоугольных импульсов, амплитуда
Рис. 4.4. Структурная схема формирователя цифрового сигнала
которых равна мгновенному значению преобразовываемогоИсигнала в отсчѐтные моменты времени. Отсчѐтные моменты времени задаются либо од-
ним из фронтов импульсов опорной последовательности, либо по некоторому |
|
уровню срабатывания УВХ. |
У |
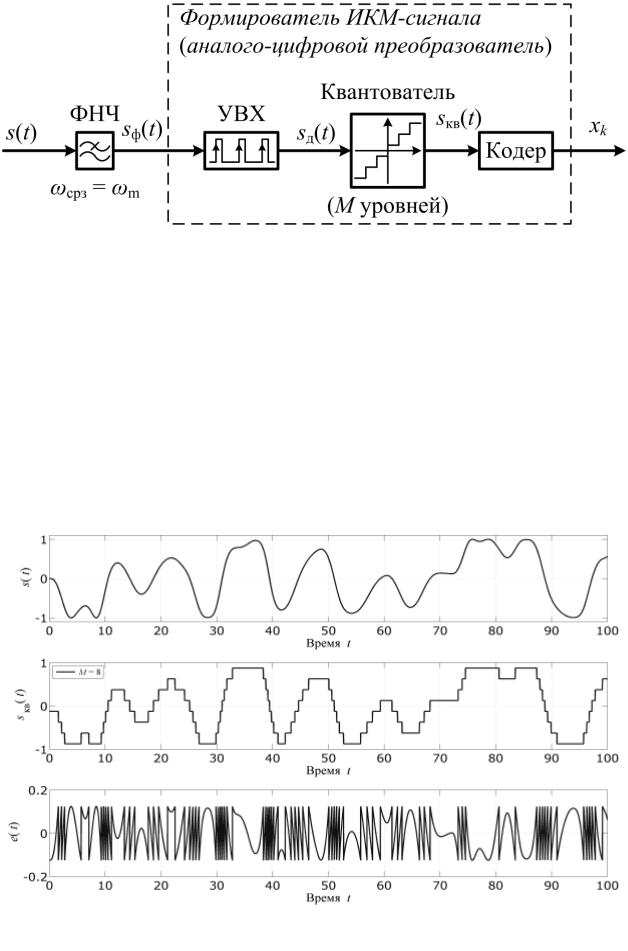
Работа 8-уровневого квантователя входного Ганалогового сигнала пока- |
|
зана на рис. 4.5. Сверху вниз показаны фрагмент реализации аналогового |
|||||||||
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
|
а |
|
сигнала, квантованный сигнал и ошибка кв нтования. Приведѐнный кванто- |
|||||||||
|
|
|
|
|
|
|
к |
|
|
ватель называется равномерным, т. . все кванты равны между собой |
|||||||||
|
|
|
|
|
|
е |
|
|
|
(см. рис. 4.6, рис. 4.7). Чем больше уровней квантования, тем больше кванто- |
|||||||||
ванный сигнал соответствует исходному аналоговому сигналу. |
|||||||||
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
л |
|
|
|
|
|
|
|
|
б |
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
|
|
Рис. 4.5. Осциллограммы процесса квантования аналогового сигнала
62
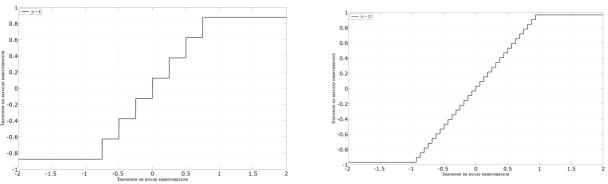
Рис. 4.6. Амплитудная характеристика Рис. 4.7. Амплитудная характеристика
квантователя с количеством уровней |
квантователя с количеством уровней |
|||||||
|
|
квантования М = 32 |
|
|||||
квантования М = 8 |
|
|
|
|
|
|||
|
|
|
|
|
|
Р |
||
Ошибка e(t) sкв (t) s(t) , |
|
|
|
|
|
|
||
неизбежно возникающая при квантовании, |
||||||||
называется ошибкой квантования. Предельная ошибка при равномерном |
||||||||
|
|
|
|
|
|
И |
|
|
квантовании равна половине шага квантования: |
У |
|
|
|||||
|
|
smax smin |
|
|
|
|||
e |
|
, |
Г |
|
|
(4.23) |
||
|
|
|
||||||
max |
|
|
2M |
|
|
|
||
где smin и smax – минимальное и максимальноБдопустимое мгновенное значение квантуемого сигнала соответственно. Для примера на рис. 4.5
emax 0,125 . Таким образом, даже при грамотном выборе частоты дискретизации сигнала квантование всегда вносит в цифровой сигнал аддитивные ис-
кажения, называемые цифровым шумом, или шумом квантования. Матема- |
||
|
к |
|
тически шум квантования явля |
р зультатом округления точного значения |
|
отсчѐта сигнала до ближайшего разрешѐнногое |
уровня. |
|
На выходе кван ва еля |
формируется сигнал с амплитуд- |
|
но-импульсной модуляцией. В практических приложениях важно, чтобы ди- |
|
и |
тся |
намический диапазон с гнала не выходил за некоторый фиксированный пре-
дел, что требует нормровки аналогового сигнала. Чаще всего для удобства
математических вык адок нормировка осуществляется по уровням 1. Если |
|
|
б |
сигнал выходит за допустимые пределы, то в квантованный сигнал вносится |
|
и |
|
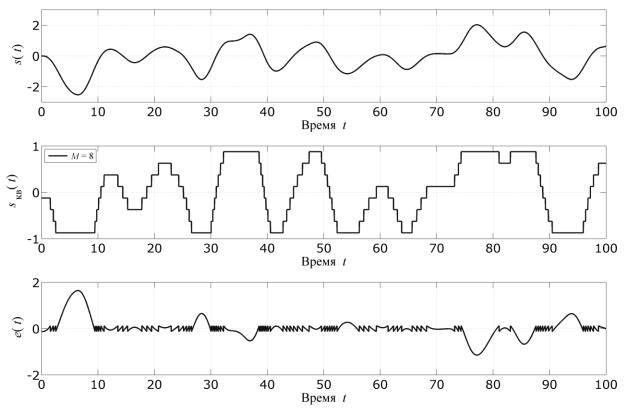
дополнительнаялпомеха, обусловленная перегрузкой квантователя |
|
(см. р с. 4.8). |
|
Б |
|
63
|
|
|
|
|
Р |
|
|
|
|
И |
|
|
|
|
У |
|
|
|
|
Г |
|
|
|
|
|
Б |
|
|
|
Рис. 4.8. Сущность эффекта перегрузки квантователя |
|
||||
|
а |
|
|
|
|
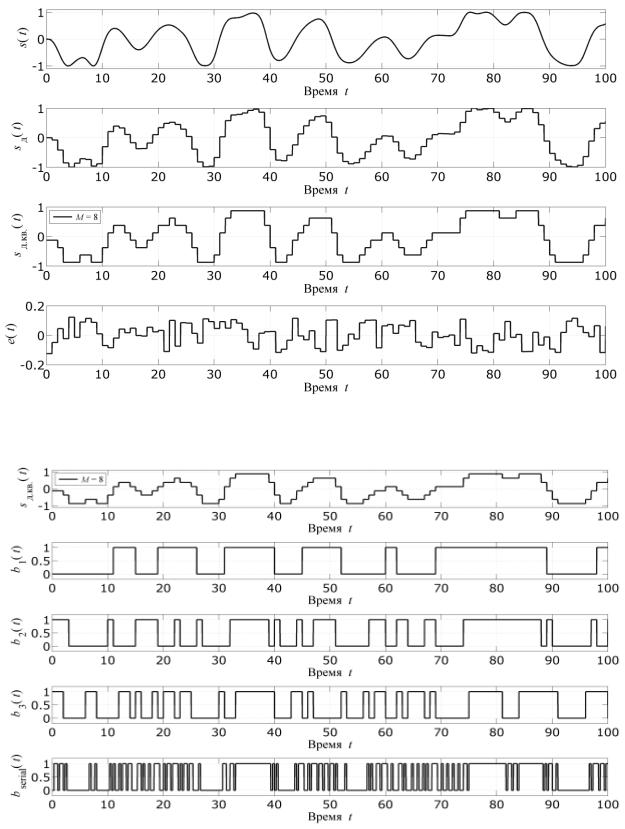
Процедура дискретизации и |
квантов |
ния налогового сигнала в полном |
|||
объѐме представлена на рис. 4.9. Сверху вниз показаны осциллограммы аналогового сигнала s(t) , дискретного во времени сигнала sд (t) , дискретного во
времени и квантованного по уровню сигнала sд.кв (t) , а также шум квантова- |
||
ния e(t) . |
о |
е |
|
|
|
Каждое из квант ванных значений дискретного во времени сигнала |
||
и |
|
|
можно представить |
параллельным двоичным кодом, как показано на |
|
рис. 4.10. В целях в зм жнстипередачи параллельного двоичного кода по одному каналулкод преобразовывается в последовательный.
Последовате ьный код формируется в течение интервала времени, не превышающегобинтервал дискретизации, путѐм последовательной передачи всехиlog(M ) ит, кодирующих квантованное значение каждого отсчѐта ис-
ходного аналогового сигнала.
БДопустимо кодировать значения отсчѐтов в системе счисления, отличной от двоичной. Для основания системы счисления q 2 количество уров-
ней квантования M qn , где n – количество разрядов, кодирующих одно со-
стояние. Разрешѐнные значения в этом случае будут кодироваться меньшим числом разрядов, однако такой вид цифрового сигнала практически нигде не используется, и в дальнейшем под цифровым сигналом будет подразумеваться только двоичный цифровой сигнал.
64
|
|
|
|
|
|
|
|
|
|
|
|
Р |
|
|
|
|
|
|
|
|
|
|
|
И |
|
|
|
|
|
|
|
|
|
|
Б |
У |
|
|
|
|
|
|
Рис. 4.9. Процесс формированияГ |
|
|
||||||
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
дискретного во времени квантованного сигнала |
|
|||||||||
|
|
|
|
|
|
|
к |
|
|
|
|
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
л |
|
|
|
|
|
|
|
|
|
|
|
б |
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
Рис. 4.10. Формирование сигнала с ИКМ: |
|
|
|||||||
|
|
|
|
|
||||||||
b1(t) – первый, или старший, бит параллельного кода; b2 (t) – второй бит параллельного кода; b3 (t) – третий, или младший, бит параллельного кода; bserial (t) – последовательный код
65
