
- •2.3.2. Джиттер
- •2.4. Математическая модель канала с замираниями
- •3.4. Избыточность источника
- •3.6. Совместная энтропия двух источников
- •3.7. Скорость передачи и пропускная способность канала связи
- •4.1.2. Представление аналоговых сигналов в дискретной форме
- •4.1.4. Дискретизация полосовых сигналов
- •4.1.5. Дискретизация сигналов в реальных системах
- •4.1.7. Выводы и практические рекомендации
- •4.2. Квантование по уровню
- •4.2.3. Техническая реализация схем квантования по уровню
- •5.4. Алгоритм Лемпеля−Зива−Велча (LZW)
- •6.1. Симметричные криптосистемы
- •6.3. Криптографический протокол
4.ДИСКРЕТИЗАЦИЯ И КВАНТОВАНИЕ СИГНАЛОВ
4.1.Дискретизация во времени
4.1.1. Вводные замечания
Для передачи по каналу связи аналоговых сообщений цифровыми методами сигнал, переносящий сообщение, должен быть представлен в цифровой форме. Процедуру, реализующую данное преобразование, называют ана- лого-цифровым преобразованием. Первым этапом аналого-цифрового преобразования является дискретизация сигнала, в результате которого формируется последовательность выборок (отсчѐтов). Значения выборок соответствуют мгновенным значениям сигнала в некоторые равноотстоящие друг от
друга моменты времени. Таким образом, на выходе устройства дискретиза- |
|||||||
|
|
|
|
|
|
|
Р |
ции формируется дискретный во времени сигнал с континуумом значений. |
|||||||
Дискретный сигнал позволяет по выборкам точно восстановить исход- |
|||||||
|
|
|
|
|
|
И |
|
ный аналоговый сигнал. Процесс дискретизация сигнала и его восстановле- |
|||||||
ния базируется на теореме В. А. Котельникова. |
|
У |
|
||||
|
|
|
|
|
|
||
|
|
|
|
Г |
|
|
|
4.1.2. Представление аналоговых сигналов в дискретной форме |
|||||||
|
|
|
Б |
|
|
|
|
Пусть s(t) − некоторый произвольный |
н логовый сигнал с ограничен- |
||||||
ным спектром, определяемым в общ мавиде комплексной функцией угловой |
|||||||
частоты S( ) S( j ) . Модуль сп |
ктральной |
плотности сигнала обозначим |
|||||
|
е |
|
|
|
|
|
|
как S( ) . Для сигнала с огранич нным спектром двухсторонняя спектраль- |
|||||||
ная плотность S( ) при | | m равна нулю. |
Угловая частота m 2 fm |
||||||
называется граничн й час |
й спектра сигнала s(t) , а сам сигнал – низкоча- |
||||||
стотным. Понят е «н зкаячастота» в данном случае является относитель- |
|||||||
ным, но не абсолютнымо. Для сигнала, формируемого датчиком температуры |
|||||||
воздуха на метеостанц , |
граничная частота |
будет порядка 10–3 Гц, для |
|||||
и |
|
|
|
|
|
|
|
аудиосигна ов – ~20 кГц, для телевизионного сигнала в классических веща- |
|||||||
тельных системах – ~6 МГц. Во всех указанных примерах сигналы называ- |
|
|
л |
ются «н зкочастотными», в англоязычной литературе – «baseband signals». В |
|
русскоязычнойблитературе иногда можно встретить понятие «видеосигнал». |
|
Каждые T секунд у сигнала берутся выборки, т. е. в данные моменты |
|
и |
|
времени определяются мгновенные значения сигнала, в результате чего фор- |
|
Бмируется последовательность импульсов (отсчѐтов) sд (t) . Значение T называется интервалом (периодом) дискретизации сигнала, величина, обратная ему, − частотой дискретизации fд 1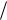 T . На практике чаще всего оперируют
T . На практике чаще всего оперируют
понятием частоты дискретизации, нежели интервалом дискретизации. Величина fд измеряется в единицах циклической частоты − герцах.
Аналитически дискретный сигнал задаѐтся следующим образом:
52

|
|
sд (t) s(kT ) s(t) T (t) s(t) (t kT ) . |
(4.1) |
k
Здесь k Z – номер отсчѐта; T (t) – опорный сигнал, представляющий собой последовательность δ -функций с периодом следования T .
Функция sд (t) представляет идеальный дискретный сигнал. При техническом осуществлении процесса дискретизации аналоговых сигналов вме-
сто -функций, в силу невозможности их физической реализации, использу- |
||
|
|
Р |
ется периодическая последовательность прямоугольных видеоимпульсов, |
||
длительность которых много меньше периода дискретизации T . |
||
4.1.3. Теорема В. А. Котельникова |
Г |
И |
|
||
|
|
|
Теория дискретизации сигналов базируется на теореме отчѐтов, сфор- |
||
m |
Бm |
|
мулированной советским академиком В. А. КотельниковымУ. Согласно теоре-
ме сигнал, спектр которого не превышает некоторую граничную частоту m ,
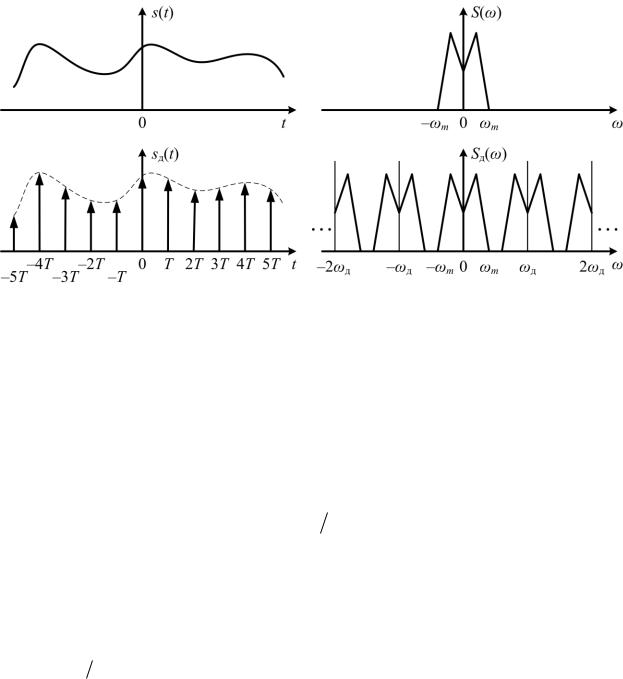
может быть точно представлен последовательностью своих отсчѐтов, взятых через равные интервалы времени T 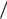 1 (2 f ) :
1 (2 f ) :
|
|
е |
а |
|
||
|
sin m (t kT ) |
|
|
|||
s(t) s(kT ) |
|
|
|
|
s(kT ) sinc m (t kT ) . |
(4.2) |
k |
m (t kT ) кk |
|
||||
|
т |
|
|
|
||
Данное интерполяционное выражение является базовым в теории ко- |
||||||
о |
|
|
|
|
|
|
дирования аналоговых ис чников. Следует отметить, что интервал времени T может быть меньше значения 1 (2 fm ) , но не превышает его. Минимально
допустимая частота д |
скретизации сигнала равна удвоенной граничной ча- |
||||||||||||||
|
|
|
|
л |
з руемого сигнала s(t) . |
|
|
|
|
|
|||||
стоте спектра дискрет |
|
|
|
|
|
||||||||||
|
|
б |
иедовательности |
T (t) определяется выражением |
|
||||||||||
Спектр пос |
|
||||||||||||||
и |
|
|
|
|
|
|
|
|
|
|
|
|
|||
Б |
|
|
|
|
|
|
S ( ) д |
( n д ) , |
|
(4.3) |
|||||
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где |
2 . |
|
|
|
|
|
|
|
|
|
|
|
|||
д |
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
Воспользовавшись свойством свѐртки двух функций, получим |
|
||||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
Sд |
( ) |
|
|
S( ) д |
( n д ) |
|
|
|
|
S( n д ) . |
(4.4) |
|||
|
|
|
|
|
|
||||||||||
|
|
|
|
|
2 |
n |
|
|
T n |
|
|||||
Здесь знак означает операцию свѐртки двух функций.
53
В частотной области операция дискретизации сигнала с ограниченным спектром означает повторение спектра исходного сигнала вдоль частотной оси. Период повторения спектра аналогового сигнала равен д 2 m или
fд 2 fm (см. рис. 4.1).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Р |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Г |
|
|
|
|
ного сигнала, не |
|
|
|
|
|
Б |
|
|
д 2 m |
или |
|||||
перекрываясь тольков том случае, если |
|||||||||||||||
|
|
|
Рис. 4.1. Преобразование |
при дискретизации сигнала |
|
||||||||||
д |
|
m |
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
Спектр S( ) |
исходного сигналаспектраповторяется в спектре Sд ( ) дискрет- |
|||||||||||||
f |
2 f |
|
|
|
|
|
|
|
част |
|
|
|
|
|
|
|
. Из рисунка видно, ч о восстановление аналогового сигнала из дис- |
||||||||||||||
|
|
|
|
|
|
|
о |
|
|
|
|
|
|
||
кретного возможно пу ѐм пропускания последнего через идеальный фильтр |
|||||||||||||||
|
|
|
|
|
и |
|
|
|
|
|
|
|
|||
нижних частот (ФНЧ) |
с |
|
той среза, заключѐнной в диапазоне от fm до |
||||||||||||
fд |
fm |
. В опт мальн м случае частота среза должна находиться посередине |
|||||||||||||
|
|
|
|
л |
|
быть равной fд |
2 . |
|
|
|
|
||||
указанного интерва а |
|
|
|
|
|||||||||||
|
Передаточная функция идеального ФНЧ определяется выражением |
|
|||||||||||||
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
б |
|
|
|
|
|
T , |
| | m ; |
|
|
|
|
||
Б |
|
|
|
|
KФНЧ ( ) |
| | m , |
|
|
|
(4.5) |
|||||
|
|
|
|
|
|
|
|
0, |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
где m T . Следовательно, |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
S( ) Sд ( )KФНЧ ( ) . |
|
|
|
(4.6) |
||
Найдя обратное преобразование Фурье, получим импульсную характеристику ФНЧ:
54
h |
(t) |
sin mt |
. |
(4.7) |
|
||||
ФНЧ |
|
mt |
||
|
|
|
||
Вычислим обратное преобразование Фурье и получим выражение для непрерывного сигнала:
|
|
|
|
|
|
sin mt |
|
|
|
|
s(t) sд (t) hФНЧ (t) s(kT ) (t kT ) |
|
|
||||||
|
mt |
|
|||||||
|
|
|
k |
|
|
|
(4.8) |
||
|
|
|
|
sin m (t kT ) |
|
|
|
||
|
|
|
|
|
|
Р |
|||
|
|
s(kT ) |
|
|
|
||||
|
|
m (t kT ) |
. |
|
|
||||
|
|
|
|
|
|||||
|
|
k |
|
|
|
|
И |
||
|
|
|
|
|
|
|
|
||
д |
Полученное выражение совпадает с общей записью теоремы Котельни- |
||||||||
m |
|
|
|
|
|
У |
|
||
кова. |
Теорема В. А. Котельникова |
налагает условие ограниченности на |
|||||||
спектр сигнала на выходе аналогового источника и определяет минимально возможную частоту дискретизации. В случае, еслиГчастота дискретизации f 2 f , происходит наложение, или перекрытиеБ, фрагментов спектра дис-
кретного сигнала. В этом случае неискажѐнное восстановление аналогового сигнала из дискретного невозможно. В реальных технических устройствах кодирования аналогового источника информ ции частоту дискретизации выбирают несколько большей, чем того требует теорема Котельникова, созда-
нием 3,4 кГц, однако частота дискр тизациик |
выбирается равной не 6,8 кГц, а |
вая в спектре дискретного сигнала |
оторый з щитный интервал. Например, |
||
не |
траспе |
|
|
в телефонии верхняя граничная частота |
сигнала определяется значе- |
||
ственно облегчает пр ек иртвание и расчѐт ФНЧ, восстанавливающего исходный сигнал из д скретн .
8 кГц. Таким образом, в спек ре дискр тного сигнала создаѐтся защитный
интервал fд 2 fm 1, 2 кГц . Введение такого защитного интервала суще-
Особым |
|
является дискретизация гармонического колебания с |
||
частотой f0 |
|
|
го |
|
. Здесь пр нц пиально необходимо, чтобы частота дискретиза- |
||||
ции была |
|
и |
fд 2 f0 , как того требует теорема |
|
fд 2 f0 |
, а не |
|||
В. А. Котельникова. Если частота дискретизации будет точно равна удвоен- |
|
|
случаем |
б |
|
и |
|
ной частоте коле ания, то возможна ситуация, когда все отсчѐты гармоническогоБколебан я будут иметь нулевые значения.
4.1.4. Дискретизация полосовых сигналов
Действительный сигнал s(t) называется полосовым, если его двухсторонний спектр везде равен нулю, за исключением интервалов ( 1; 2 ) и( 2 ; 1) , где 1 2 f1 , 2 2 f2 . Такой сигнал можно рассматривать как узкополосный процесс, для которого выполняется условие
55
|
|
|
|
f |
1, |
(4.9) |
|
|
|
0 |
|
f0 |
|||
|
|
|
|
|
|
||
где |
2 f |
2 1 – ширина |
|
полосы частот аналогового |
сигнала; |
||
0 |
2 f0 ( 1 |
2 ) 2 – центральная частота спектра. |
|
||||
Согласно теореме В. А. Котельникова частота дискретизации должна быть не менее 2 f2 . Однако в рассматриваемом случае это значение частоты
слишком велико для корректной дискретизации и последующего восстановления полосового сигнала. В действительности минимальная частота дискре-
тизации полосового сигнала определяется нижней граничной частотой f1 , |
|||||||||||||
|
|
|
|
|
|
f2 , а также их разницей f |
|
И |
|||||
верхней граничной частотой |
f2 f1 – шириной |
||||||||||||
полосы частот (см. рис. 4.2). |
|
|
|
|
У |
Р |
|||||||
|
|
|
|
|
|
|
|
|
Г |
|
|
||
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
|
|
|
|
|
|
к |
|
|
|
|
|
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|||
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
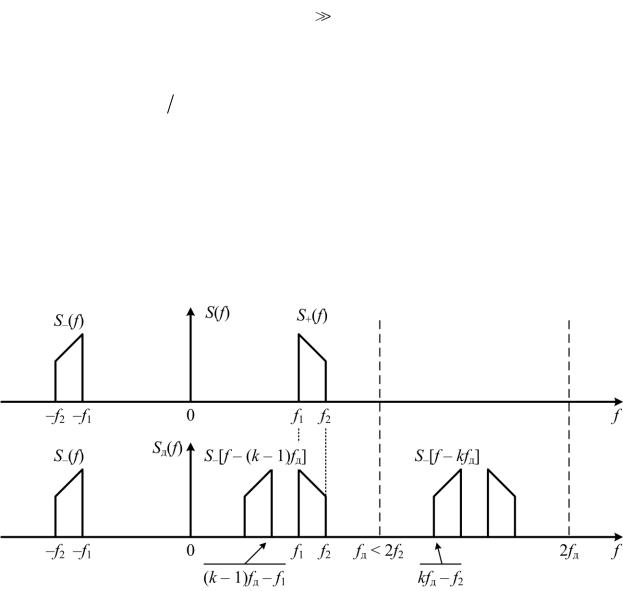
Рис. 4.2. Спектральное преобразование при дискретизации полосового сигна- |
|||||||||||||
|
б |
|
|
|
|
|
ла |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
Согласнолрис. 4.2, спектральная плотность исходного аналогового сиг- |
|||||||||||||
нала может ыть представлена суммой двух функций, |
|
первая из которых |
|||||||||||
определена для отрицательных частот, вторая – для положительных: |
|||||||||||||
Б |
|
|
|
|
S( f ) S ( f ) S ( f ) . |
|
|
|
(4.10) |
||||
|
когда |
f |
д |
2 f |
2 , при дискретизации полосового сигнала во- |
||||||||
В случае, |
|
|
|||||||||||
круг его спектра положительных частот слева и справа формируются два фрагмента его спектра отрицательных частот. Отсюда следует, что частота дискретизации fд должна быть выбрана таким образом, чтобы верхняя ча-
стота спектрального фрагмента S |
f |
(k 1) f |
|
не превышала значения |
f |
, |
|
|
|
д |
|
1 |
|
56 |
|
|
|
|
|
|
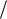
а нижняя частота спектрального фрагмента S |
f |
kf |
|
была не меньше, чем |
|
|
|
д |
|
значения f2 . В этом случае спектр исходного полосового сигнала не пере-
крывается соседними фрагментами спектра дискретного сигнала, что допускает неискажѐнное восстановление аналогового сигнала из дискретного путѐм пропускания последнего через идеальный полосовой фильтр.
Для определения частоты дискретизации полосового сигнала запишем систему неравенств:
(k 1) f |
д |
f |
f ; |
|
|
1 |
1 |
Р |
|
|
|
|
|
|
|
f2 , |
|
(4.11) |
|
kfд f2 |
|
|
||
|
|
|
|
|
где k – натуральное число. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Так как f1 f2 f |
, то выражение (4.11) можно привести к виду |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Г |
|
|
|
|
|
|
|
1 k |
|
f2 |
|
|
|
kfд |
|
|
У |
|
|||||||||||
|
|
|
|
|
|
|
|
|
. |
Б |
(4.12) |
||||||||||||||
|
|
|
|
f |
2 f |
||||||||||||||||||||
Или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k 1 |
fд |
|
|
f |
2 |
|
1. |
|
|
(4.13) |
||||||||||
|
|
|
|
|
|
|
2 |
|
f |
|
f |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Минимально возможная допустимаячастота дискретизации полосового |
|||||||||||||||||||||||||
сигнала определяется выражени м |
|
|
к |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
т |
|
|
|
2 f2 |
|
|
|
|
|
||||||||||||
|
|
|
|
|
f |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
(4.14) |
|
|
|
|
|
|
|
д minе |
f |
|
|
|
|
||||||||||||||
|
|
|
означает |
|
|
|
|
|
f |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||
где операция |
X |
|
|
|
|
|
перацию округления числа X до ближайшего |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
целого, не превышающего X. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
л |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
На рис. 4.3 пр ведено пространство допустимых частот дискретизации |
|||||||||||||||||||||||||
полосового сигна а в зав симости от отношения верхней граничной частоты |
|
|
б |
спектра сигна а к по осе занимаемых им частот. Заштрихованные области |
|
и |
|
соответствуют недопустимым значениям частоты дискретизации полосового |
|
сигнала. |
|
Б |
|
57
