
- •2.3.2. Джиттер
- •2.4. Математическая модель канала с замираниями
- •3.4. Избыточность источника
- •3.6. Совместная энтропия двух источников
- •3.7. Скорость передачи и пропускная способность канала связи
- •4.1.2. Представление аналоговых сигналов в дискретной форме
- •4.1.4. Дискретизация полосовых сигналов
- •4.1.5. Дискретизация сигналов в реальных системах
- •4.1.7. Выводы и практические рекомендации
- •4.2. Квантование по уровню
- •4.2.3. Техническая реализация схем квантования по уровню
- •5.4. Алгоритм Лемпеля−Зива−Велча (LZW)
- •6.1. Симметричные криптосистемы
- •6.3. Криптографический протокол

Сообщение |
Выбранное имя |
Криптотекст |
К |
Королѐв |
5643452 |
О |
Орехов |
3572651 |
Р |
Рузаева |
4673956 |
O |
Осипов |
3517289 |
Б |
Батурин |
7755628 |
К |
Кирсанова |
1235267 |
А |
Арсеньева |
8492746 |
Криптотекстом будет являться цепочка номеров, записанных в порядке их выбора в справочнике. Чтобы затруднить расшифровку, следует выбирать случайные имена, начинающиеся на нужную букву. Таким образом, исход-
ное сообщение может быть зашифровано множеством различных списков |
|
номеров (криптотекстов). |
Р |
|
|
Чтобы расшифровать текст, надо иметь справочник, составленный со- |
|||
гласно возрастанию номеров. Этот справочник является лазейкойИ(секрет, ко- |
|||
|
|
|
У |
торый помогает получить начальный текст), известной только легальным |
|||
|
Б |
|
|
пользователям. Не имея на руках копии справочника, криптоаналитик затра- |
|||
тит очень много времени на расшифровку. |
|
Г |
|
а |
|
|
|
к |
|
|
|
6.3. Криптографический прото ол |
|
|
|
ный или конкретный протокол, включающий набор криптографических ал-
горитмов. В основе про окола набор правил, регламентирующих ис-
Криптографический протоколлежит(Cryptographic protocol) – это абстракт-
пользование криптографических преобразований и алгоритмов в информа- |
||||
ционных процессах. |
|
|||
|
Существуют следующиетосновные виды криптографических протоко- |
|||
лов: |
|
|
|
о |
|
|
|
|
|
|
– протоко ы ш фрования / расшифрования; |
|||
|
|
и |
||
|
– протоко ы э ектронной цифровой подписи (ЭЦП); |
|||
|
– протоко ы идентификации / аутентификации; |
|||
|
|
л |
|
|
|
– протоколы аутентифицированного распределения ключей. |
|||
|
Протоколыб |
шифрования / расшифрования. В основе протокола этого |
||
и |
|
|
|
|
Б |
|
|
|
|
класса содержится некоторый симметричный или асимметричный алгоритм шифрования/расшифрования. Алгоритм шифрования выполняется на передаче отправителем сообщения, в результате чего сообщение преобразуется из открытой формы в шифрованную. Алгоритм расшифрования выполняется на приѐме получателем, в результате чего сообщение преобразуется из шифрованной формы в открытую. Так обеспечивается свойство конфиденциальности.
Для обеспечения свойства целостности передаваемых сообщений симметричные алгоритмы шифрования / расшифрования обычно совмещаются с
88
алгоритмами вычисления имитозащитной вставки (ИЗВ) на передаче и проверки ИЗВ на приѐме, для чего используется ключ шифрования. При использовании асимметричных алгоритмов шифрования / расшифрования свойство целостности обеспечивается отдельно путем вычисления электронной цифровой подписи (ЭЦП) на передаче и проверки ЭЦП на приѐме, чем обеспечиваются также свойства безотказности и аутентичности принятого сообщения.
Протоколы электронной цифровой подписи (ЭЦП). В основе протокола этого класса содержится некоторый алгоритм вычисления ЭЦП на передаче с помощью секретного ключа отправителя и проверки ЭЦП на приѐме с помо-
щью соответствующего открытого ключа, извлекаемого из открытого спра-
рация архивирования может не выполняться, если ЭЦП используетсяРтолько для обеспечения свойств целостности и аутентичности принятого сообщения,
вочника, но защищенного от модификаций. В случае положительного ре-
зультата проверки протокол обычно завершается операцией архивирования
принятого сообщения, его ЭЦП и соответствующего открытого ключа. Опе-
но не безотказности. В этом случае после проверки ЭЦП может быть уни- |
|||
|
|
|
И |
чтожена сразу или по прошествии ограниченного промежутка времени ожи- |
|||
дания. |
|
У |
|
|
|
||
Протоколы идентификации/аутентификации. В основе протокола |
|||
|
Г |
|
|
|
Б |
|
|
идентификации содержится некоторый алгоритм проверки того факта, что |
|||
вестную только заявленному объе тук, причемаметод проверки является, конечно, косвенным, т. е. без предъявл ния этой секретной информации.
идентифицируемый объект (пользователь, устройство, процесс, …), предъ-
явивший некоторое имя (идентификатор), зн ет секретную информацию, из-
Обычно с каждым именем (ид нтификатором) объекта связывается пе-
речень его прав и полномочий в сист ме, записанный в защищенной базе |
|
данных. В этом случае |
е |
окол идентификации может быть расширен до |
|
ной информации грает секретный ключ ЭЦП, а проверка ЭЦП осуществля-
протокола аутентификации, в ко ором идентифицированный объект прове- |
|
ряется на правомочн сть заказываемой услуги. |
|
|
т |
Если в проток ле дентификации используется ЭЦП, то роль секрет- |
|
про |
|
и |
|
ется с помощью открытого ключа ЭЦП, знание которого не позволяет опре-
делить соответствующий секретный ключ, но позволяет убедиться в том, что |
||
он |
|
авторулЭЦП. |
|
Протоколы аутентифицированного распределения ключей. Протоколы |
|
|
|
б |
этого класса совмещают аутентификацию пользователей с протоколом гене- |
||
рации |
распределения ключей по каналу связи. Протокол имеет двух или |
|
|
известен |
|
Б |
|
|
трѐх участников; третьим участником является центр генерации и распределения ключей (ЦГРК), называемый для краткости сервером S. Протокол состоит из трѐх этапов: генерации, регистрации и коммуникации. На этапе генерации сервер S генерирует числовые значения параметров системы, в том числе свой секретный и открытый ключ. На этапе регистрации сервер S идентифицирует пользователей по документам (при личной явке или через уполномоченных лиц), генерирует ключевую и/или идентификационную информацию для каждого объекта и формирует маркер безопасности, содержа-
89
щий необходимые системные константы и открытый ключ сервера S (при необходимости). На этапе коммуникации реализуется собственно протокол аутентифицированного ключевого обмена, который завершается формированием общего сеансового ключа.
6.4.Управление ключами
Управление ключами состоит из процедур, обеспечивающих:
– включение пользователей в систему; |
|
|
Р |
|
– выработку, распределение и введение в аппаратуру ключей; |
||||
|
||||
– контроль использования ключей; |
|
И |
||
– смену и уничтожение ключей; |
|
|||
|
|
|
||
– архивирование, хранение и восстановление ключей. |
|
|
||
|
У |
|
||
Управление ключами как основа для обеспечения конфиденциальности |
||||
обмена информацией, идентификации и целостности данных играет важней-
безопасности многочисленных ключей к проблемеГобеспечения безопасности нескольких ключей, которая может быть относительно просто решена путем
шую роль в криптографии. Важным свойством хорошо спроектированной си-
обеспечения их физической изоляции в выделенныхБпомещениях и защищенном от проникновения оборудовании. В случ е использования ключей для
стемы управления ключами является сведение сложных проблем обеспечения
обеспечения безопасности хранимой информации субъектом может быть единственный пользователь, который осущ ствляет работу с данными в последова-
к тельные промежутки времени. Управление ключами в сетях связи включает, по
крайней мере, двух субъектов – отправит ля и получателя сообщения.
Целью управления ключами является нейтрализация таких угроз, как:
– компрометация к нфиденциальности закрытых ключей; |
|||||
– компрометация аутентичности закрытых или открытых ключей. При этом |
|||||
|
|
|
|
|
т |
|
|
|
|
о |
|
|
|
|
и |
|
|
под аутентичностью п н мается знание или возможность проверки идентичности |
|||||
|
|
для |
|
|
|
корреспондента, |
|
обеспечения конфиденциальной связи с которым использу- |
|||
ется данный к юч; |
|
|
|||
|
б |
|
|
|
|
– несанкционированное использование закрытых или открытых ключей, |
|||||
Сроки |
|
|
|
|
|
например, использование ключа, срок действия которого истек. |
|||||
Б |
|
действия ключей. Одной из важных характеристик системы |
|||
управлен я ключами являются сроки действия ключей. Срок действия ключа означает промежуток времени, в течение которого он может быть использован доверенными сторонами.
Сокращение сроков действия ключей необходимо для достижения следующих целей:
–ограничения объѐма информации, зашифрованной на данном ключе, которая может быть использована для криптоанализа;
–ограничения размера ущерба при компрометации ключей;
–ограничения объѐма машинного времени, которое может быть ис-
пользовано для криптоанализа.
90
В дополнение к указанной выше классификации ключей по уровням может быть введена также следующая классификация.
–ключи с длительным сроком действия. К ним относится главный ключ, часто – ключи для шифрования ключей;
–ключи с коротким сроком действия. К ним относятся ключи для шифрования данных.
Как правило, в телекоммуникационных приложениях используются ключи с коротким сроком действия, а для защиты хранимых данных – с длительным сроком действия. Необходимо иметь в виду, что термин «короткий
срок действия» относится только к сроку действия ключа, а не к промежутку времени, в течение которого ключ должен оставаться в секрете. НапримерР, к ключу, используемому для шифрования в течение только одного сеанса связи, часто предъявляется требование, чтобы зашифрованная наИнѐм информация не могла быть вскрыта на протяжении нескольких десятков лет. В то же время электронная подпись проверяется немедленно послеУпередачи сообщения, поэтому ключ подписи должен сохраняться в тайне в течение достаточно короткого срока. Г
Жизненный цикл ключей. Ключевая информацияБдолжна быть сменена до момента истечения срока действия ключа. Для этого могут быть исполь-
зованы действующая ключевая информация, протоколы распределения ключей и ключевые уровни. Для того чтобыаснизить ущерб от компрометации ключей, следует избегать зависимостейкмежду действующей и устанавливаемой ключевой информацией. Например, не рекомендуется защищать очередной сеансовый ключ с помощьюед йствующего сеансового ключа. При хранении закрытых ключей должны быть приняты меры по обеспечению их конфиденциальности и аутентичностит . При хранении открытых ключей должны быть приняты меры, позволяющие проверить их аутентичность. Конфиденциальностьрованыи ау ен ичнос ь могут быть обеспечены криптографическими, организациинными и техническими мерами.
Все криптос стемы, за исключением простейших, в которых используемые ключи зафлкс раз и навсегда, нуждаются в периодической за-б
и |
|
ключи от момента установления до следующей замены (жизненный цикл |
|
Б |
|
ключей). |
|
1. |
Регистрация пользователей. Эта стадия включает обмен первона- |
чальной ключевой информацией, такой, как общие пароли или PIN-коды, пу- |
|
тем личного общения или пересылки через доверенного курьера. |
|
2. |
Инициализация. На этой стадии пользователь устанавливает ап- |
паратное оборудование и/или программные средства в соответствии с установленными рекомендациями и правилами.
3. Генерация ключей. При генерации ключей должны быть приняты меры по обеспечению их необходимых криптографических качеств. Ключи могут генерироваться как самостоятельно пользователем, так и специальным
91
защищенным элементом системы, а затем передаваться пользователю по защищенному каналу.
4. Установка ключей. Ключи устанавливаются в оборудование тем или иным способом. При этом первоначальная ключевая информация, полученная на стадии регистрации пользователей, может либо непосредственно вводиться в оборудование, либо использоваться для установления защищенного канала, по которому передается ключевая информация. Эта же стадия используется в последующем для смены ключевой информации.
5. Регистрация ключей. Ключевая информация связывается регистрационным центром с именем пользователя и сообщается другим пользователям ключевой сети. При этом для открытых ключей создаются сертификационным центром ключевые сертификаты, и эта информация публикуется тем или иным способом.
6. |
Обычный режим работы. На этой стадии ключи используются |
||||
для защиты информации в обычном режиме. |
|
|
|
Р |
|
|
|
|
|
||
7. |
Хранение ключа. Эта стадия включает процедуры, необходимые |
||||
|
|
|
|
И |
|
для хранения ключа в надлежащих условиях, обеспечивающих его безопас- |
|||||
ность до момента его замены. |
|
У |
|
||
|
|
|
|
||
8. |
Замена ключа. Замена ключа осуществляется до истечения его |
||||
|
|
Г |
|
|
|
|
|
Б |
|
|
|
срока действия и включает процедуры, связанные с генерацией ключей, про- |
|||||
токолами обмена ключевой информацией между корреспондентами, а также с доверенной третьей стороной. Для открытых ключей эта стадия обычно
включает обмен информацией по защищенному каналу с сертификационным |
|||||
центром. |
|
|
|
|
а |
|
|
|
кльных случаях ключевая информация по- |
||
9. |
Архивирование. В отд |
||||
сле еѐ использования для |
|
|
информации может быть подвергнута ар- |
||
|
|
|
е |
|
|
|
|
защиты |
|
|
|
хивированию для еѐ извлечения со специальными целями (например, рас- |
|||||
смотрения вопросов, связанных с о казами от цифровой подписи). |
|||||
10. Уничтожение ключей. После окончания сроков действия ключей |
|||||
они выводятся з обращения, и все имеющиеся их копии уничтожаются. При |
|||||
этом необходимо с ед ть, |
чтобы в случае уничтожения закрытых ключей |
||||
тщательно уничтожа ась и вся информация, по которой возможно их частич- |
||||
|
|
|
и |
|
ное восстанов ение. |
|
|||
|
11. Восстановлениел |
ключей. Если ключевая информация уничтоже- |
||
|
|
б |
|
|
на, но не скомпрометирована (например, из-за неисправности оборудования |
||||
Б |
|
|
|
|
или |
з-за того, что оператор забыл пароль), должны быть предусмотрены ме- |
|||
ры, |
дающие возможность восстановить ключ из хранимой в соответствую- |
|||
щих условиях его копии. |
|
|||
12. Отмена ключей. В случае компрометации ключевой информации возникает необходимость прекращения использования ключей до окончания срока их действия. При этом должны быть предусмотрены необходимые меры оповещения абонентов сети. При отмене открытых ключей, снабженных сертификатами, одновременно производится прекращение действия сертификатов.
92
7. ПОМЕХОУСТОЙЧИВОЕ КОДИРОВАНИЕ В СИСТЕМАХ ЦИФРОВОЙ РАДИОСВЯЗИ
7.1. Необходимость канального кодирования
Общее требование, предъявляемое к любой СПИ, состоит в достоверном и своевременном получении заданного объѐма информации из излучений с ограниченной энергией. Ошибочные, запоздалые или неполные сведения обесценивают полученную информацию, так как не позволяют оперативно принимать правильные решения.
Достоверному приѐму информации по реальным радиоканалам препят-
ствуют следующие факторы: |
|
|
|
|
случайные искажения радиосигнала при распространении элек- |
||
тромагнитных волн; |
|
Р |
|
|
|
||
|
неизбежное наличие внешних и внутренних помех; |
|
|
|
|
И |
|
техническое несовершенство устройств передачи, приѐма и обра- |
|||
ботки сигналов – переносчиков информации. |
У |
|
|
|
|
|
|
Улучшение качества приѐма из-за технического несовершенства аппа- |
|||
ратуры в принципе может быть достигнуто путѐм еѐГулучшения. Что же ка- |
|||
сается помех и искажений радиосигнала, то нивелированиеБ их влияния носит принципиальный характер, обусловленный х р ктеристиками сигнала, ра-
диоканала и приѐмника. Радиоканал является одним из самых сложных кана-
лов передачи информации в смысле обеспечения заданного качества переда- |
||||||
|
|
|
|
|
а |
|
чи информации. Использование СПИ в различных сферах жизнедеятельности |
||||||
человека ставит дополнительные |
|
к |
||||
|
|
бования к защите информации от попы- |
||||
ток несанкционированного дос упа к |
|
. |
||||
|
|
ней |
|
|||
В настоящее время фундамен альные задачи передачи и приѐма радио- |
||||||
сигналов сводятся к следующим |
|
рѐм: |
|
|||
1) генерац я с гнал в, |
беспечивающих повышенную помехозащи- |
|||||
|
тр |
|
|
|
||
щѐнность, скрытностьозащиту информации от несанкционированного до- |
||||||
и |
|
|
|
|
|
|
2)созданиеб о ьших ансамблей сигналов с «хорошими» взаимокорреляционнымипомехамисвойствами (для систем с множественным доступом);
3)опт мальный приѐм радиосигналов и выделение сообщений в каналахБс .
Во многих практических случаях приѐм сигналов должен осуществляться при очень малых отношениях сигнал/помеха в силу ограниченнойступа; л
единицы, выбирается преднамеренно.
Основной задачей помехоустойчивого кодирования является решение проблемы обеспечения заданной достоверности передаваемых данных за счѐт применения специальных устройств кодирования–декодирования в составе систем цифровой радиосвязи.
93
К наиболее эффективным методам обеспечения высокого качества цифровой передачи в условиях высокого уровня шума канала относятся уже весьма мощные в настоящее время алгоритмы кодирования/декодирования с использованием корректирующих кодов. За 50 лет своего интенсивного развития в технику связи были успешно внедрены пороговые декодеры, алгоритм Витерби, коды Рида–Соломона, каскадные схемы кодирования, а также разработки последнего времени: алгоритмы для турбокодов и многопороговые декодеры (МПД). Требования к алгоритмам исправления ошибок в каналах с шумами, в частности, спутниковых каналах, непрерывно растут, и
главная проблема − декодирование с эффективностью, близкой к оптимальной по энергетике канала, но при максимально простой реализации, – еще до недавнего времени была весьма далека от своего успешного решения.
методов канального кодирования является микроэлектроникаИ. ВРнастоящее время практически нет ограничений на вычислительную сложность канальных кодеров-декодеров (кодеков), как, например, при турбокодировании.
Технологической основой разработки и внедрения высокоэффективных
Другим, еще более эффективным подходом к решению проблемы син-
теза высокоэффективных декодеров являются многопороговые декодеры. |
|
|
У |
Г |
|
Б |
|
Указанный метод широко используется как для блочных, так и для свѐрточ-
ных кодов, в том числе и недвоичных. В настоящее время алгоритмы типа
МПД могут декодировать длинные коды почти так же, как и оптимальные
переборные алгоритмы. Однако сами МПД сохраняют при этом линейную
сложность реализации. При одина овой эффективности МПД выполняет |
|||||
|
|
|
|
|
е |
примерно в 100 раз меньшее число оп раций, чем соответствующие турбоде- |
|||||
кодеры. При аппаратной реализациикМПД может быть в некоторых случаях |
|||||
|
|
|
|
т |
|
более быстрым, чем турбодекод ры, почти на 3 десятичных порядка. |
|||||
|
|
|
о |
|
|
7.2. Общие принципы помехоустойчивого кодирования |
|||||
|
|
и |
|
|
|
и декодирован я |
|
|
|||
|
л |
|
|
|
|
Применен е кодов, исправляющих ошибки, является эффективным |
|||||
б |
|
|
|
|
|
средством повышения достоверности передачи информации при сохранении |
|||||
и |
|
|
|
|
|
неизменными скорости передачи и энергетических параметров сигнала или при сн жен и отношения сигнал/шум, требуемого для обеспечения заданной дБдостоверности приема информации. Так, современные помехоустойчивые коды позволяют снизить отношение сигнал/шум до 6–8 дБ. Для примера – в космических или спутниковых системах снижение отношения сигнал/шум на 1 эквивалентно снижению стоимости аппаратуры на 1 млн дол. США.
Теоретически эффективность помехоустойчивого кодирования была доказана Шенноном еще в 1948 г. Он показал, что если скорость передачи информации от некоторого источника меньше пропускной способности канала связи, то, применяя избыточное кодирование, можно обеспечить безошибочную передачу сообщения через канал связи. Внедрение помехоустой-
94
чивого кодирования сдерживалось отсутствием необходимых аппаратных средств.
Теория помехоустойчивого кодирования базируется на достаточно сложном математическом аппарате, в частности, на высшей алгебре.
Основу помехоустойчивого кодирования составляет введение в передаваемые сообщения некоторой избыточности. Например, в нашей речи вероятны ошибки, но это не мешает правильному пониманию содержания, если этих ошибок немного. Это касается как самих слов, так и связности слов в предложениях. Наша речь избыточна.
Введение избыточных символов пропорционально длине блока, т. е. относительное количество избыточных символов в блоках различной длины не зависит от длины блока. Чем длиннее блок, тем больше ошибок может быть исправлено и тем выше помехозащищенность передаваемого сообще-
ния. Но с ростом длины блока растет и сложность декодера, и задержка при |
|||||||
|
|
|
|
|
|
|
Р |
передаче сигнала. Большое влияние на выбор кода и алгоритма его декоди- |
|||||||
рования оказывает канал связи. |
|
|
|
|
|
И |
|
Три модели каналов связи перечислены ниже. |
|
|
|
||||
|
|
|
|
|
|||
1. Двоичный симметричный канал (ДСК) без памяти. |
|
|
|||||
|
|
|
|
|
У |
|
|
2. Дискретный канал без памяти. |
|
|
Г |
|
|
||
3. Дискретный канал с памятью. |
|
|
|
|
|||
|
|
|
|
|
|
|
|
В первом случае на входе модулятора и выходе демодулятора имеются |
|||||||
|
|
Б |
|
|
|
||
только двоичные символы (0,1) и демодулятор принимает жесткие решения – |
|||||||
|
а |
|
|
|
|
|
|
к |
|
|
p -ичные символы, а на |
||||
0,1. В дискретном канале без памяти на входе имеем |
|||||||
выходе – q -ичные. Дискретный канал с памятью – это канал с замираниями. |
|||||||
Кодирование представляет собой пр образование последовательности ин-
формационных символов {ai} в последовательность кодированных символов |
||||||||
|
|
|
|
|
е |
|
|
|
{ bi bi}. Наиболее наглядно акое преобразование можно представить в таб- |
||||||||
личном виде. |
|
|
т |
|
|
|||
|
|
|
|
|
|
|
||
|
|
|
|
о |
|
|
||
|
|
|
|
ai |
|
bi |
|
|
|
|
|
|
00 |
|
|
100 |
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
01 |
|
|
010 |
|
|
|
|
л |
|
|
|
|
|
|
|
|
10 |
|
|
001 |
|
|
|
|
б |
11 |
|
|
111 |
|
|
|
Рассмотрим общие принципы кодирования. Пусть на вход канала по- |
|||||||
|
и |
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
|
ступает некий сигнал S( t ) , а на выходе имеем уже другой сигнал S* ( t ) . Пусть эти сигналы являются элементами некоторого множества. На этом множестве вводится метрика D(S* , S j ) , т. е. ищется минимальное расстояние
между любыми парами сигналов S |
( t ) и |
S (t) – элементами данного мно- |
i |
|
j |
жества. Выбирается та пара сигналов, где эта метрика минимальна.
95
T |
S( t ) S * ( t ) 2dt . |
|
D( S ,S*) |
(7.1) |
|
0 |
|
|
Выражение (7.1) наиболее справедливо, если в канале связи рассматривается аддитивный белый гауссовский шум. Декодер, минимизирующий функцию (7.1), называют декодером максимального правдоподобия.
Вычислить среднеквадратичную метрику для всего ансамбля сигналов Si ( t ) достаточно сложно; индекс i принадлежит интервалу 0 i qk , q – ос-
нование кода, k |
– количество информационных символов в кодовой после- |
|
Р |
довательности. Иногда для упрощения процедуры вычисления функции (7.1) используют не сами сигналы Si ( t ) и Si* ( t ) , а их цифровые представления. Дальнейшее упрощение процедуры вычисления – это q 2 . Такие двоичные
решения на практике называют жесткими. |
У |
|
|
Принятие демодулятором жестких решений соответствует модели |
|
ДСК. Получаемая при таком методе приема метрика равна Ичислу несовпаде- |
|
ний символов между принимаемой последовательностью и опорной и назы- |
|||
вается метрикой Хемминга, или хемминговым расстоянием. |
|||
В процессе работы кодер помехоустойчивогоГкода в соответствии с не- |
|||
которыми правилами осуществляет |
|
входных символов. В зависи- |
|
мости от количества возможных значений Q Бк ждого из символов все коды |
|||
можно разделить на двоичные − при Q 2 − и недвоичные − при Q 2. |
|||
Линейные коды образуют в торное пространство и обладают следу- |
|||
|
|
обработку |
|
ющим важным свойством: два кодовыхслова можно сложить, используя |
|||
подходящее определение суммы, и получить третье кодовое слово. В случае |
|||
обычных двоичных кодов э а операция является посимвольным сложением |
|||
двух кодовых слов |
м дулю 2. |
Данное свойство существенно упрощает |
|
процедуры кодированияпоитдекодирования, а также задачу вычисления параметров кода, поск льку минимальное расстояние между двумя кодовыми словами при этом экв валентно минимальному расстоянию между кодовым
словом, состоящ м цел ком из нулей, и некоторым другим кодовым словом. |
||
|
|
и |
Таким о разом, при вычислении характеристик линейного кода достаточно |
||
рассмотреть,лчто происходит при передаче кодового слова, состоящего цели- |
||
ком з нулей. |
|
|
|
б |
|
и |
|
|
7.3. Классификация помехоустойчивых кодов |
||
Б |
|
|
В настоящее время разработаны и широко используются несколько |
||
различных классов помехоустойчивых кодов, отличающихся друг от друга структурой, функциональным назначением, энергетической эффективностью, алгоритмами кодирования и декодирования. Помехоустойчивые коды условно могут быть разделены на следующие классы:
1) блочные и свѐрточные (древовидные) коды;
96
2)линейные и нелинейные коды;
3)систематические и несистематические коды;
4)циклические и нециклические коды;
5)двоичные и недвоичные коды;
6)исправляющие независимые ошибки и исправляющие пакетные
ошибки;
7)каскадные и некаскадные коды.
Представленную выше классификацию можно разбить на две группы кодов: блоковые и древовидные.
Блоковый кодер – устройство без памяти, преобразующее одну после-
ных блоковых кодов непрерывная последовательность информационныхРбит разбивается на блоки по k бит. Все дальнейшие операции по кодированию и
довательность в другую. Кодер древовидного кода – устройство с памятью.
Блоковый код представляет собой множество последовательностей
декодированию производятся с блоками. Каждому информационномуИ блоку из k бит ставится в соответствие блок из n символов, где n k . Этот блок из
символов, которые называют кодовыми словами. При использовании двоич-
ся минимальным расстоянием, или расстоянием Хэмминга, между любыми двумя кодовыми словами длиной n .
n символов называют кодовым словом B , которое передается по каналу свя- |
|||||||
|
|
|
i |
|
|
У |
|
зи, искажается и декодируется независимо от других блоков. Величину n |
|||||||
|
|
|
|
|
Г |
в дво- |
|
называют длиной кодового слова. Число различных кодовых слов m |
|||||||
ичном блоковом коде с параметрами ( n,k ) р вно |
2k . |
|
|
||||
Основными |
параметрами блочного |
Б |
|
кода |
|||
|
являются: скорость |
||||||
R k / n , минимальное кодовое расстояние |
dmin |
между любой парой кодо- |
|||||
вых слов данного кода и вес w( B ) |
|
ода |
|
|
|
||
одового слова B , определяемый как чис- |
|||||||
ло ненулевых символов в кодовом |
к |
|
|
|
|
||
|
B . Последний параметр определяет- |
||||||
|
слове |
|
|
|
|
|
|
f d 1 ошибок |
справ тьt ( d 1) / 2 |
ошибок. Так, при d 3 код спо- |
|||||
Любой двоичный бл к вый код с dmin d |
способен обнаружить любые |
||||
|
|
и |
|
|
|
|
л |
|
|
|
|
собен исправить одну ошбку и обнаружить две. |
|||||
б |
|
|
|
|
|
Совершенные коды позволяют исправить все ошибки кратности и ни |
|||||
одной оши ки о ее высокой кратности. |
|
|
|||
и |
|
|
|
|
|
7.4. Блочное линейное кодирование |
|
||||
Значительная часть кодирующих схем, применяемых на практике, |
|||||
предполагаетБ |
использование линейных кодов. |
Блочный код длиной n с 2k |
|||
словами называется линейным (n, k)-кодом, если его кодовые слова образуют k-мерное подпространство Vk векторного n-мерного пространства Vn . Под-
пространство Vk порождается базисом из k линейно независимых векторов, которые образуют строки порождающей матрицы (n, k)-кода
97

|
g0 |
|
|
g0,0 |
|
g |
|
|
g |
G |
1 |
|
|
1,0 |
|
|
|
|
|
|
|
|
|
|
gk 1 |
|
gk 1,0 |
||
g0,1 |
g0,n 1 |
|
|
|
||
g1,1 |
|
|
|
|
|
|
g1,n 1 |
. |
(7.2) |
||||
|
|
|
|
|||
|
|
|||||
gk 1,1 |
|
|
|
|
|
|
gk 1,n 1 |
|
|
||||
Процесс кодирования блочного кода состоит в разбиении информаци- |
||||||||||
онной последовательности |
на |
сообщения U u0 , u1, ...,uk 1 |
длиной k и |
|||||||
отображении этих сообщений в кодовые слова C c0 , c1, ...,cn 1 длиной n : |
||||||||||
|
|
|
C UG . |
|
|
|
|
|
(7.3) |
|
Кодовые слова |
можно |
представлять в систематической форме |
||||||||
C (U, V) , |
образуя отдельно информационную часть U из k |
Р |
|
|||||||
символов и |
||||||||||
|
|
|
|
|
|
|
|
И |
|
|
|
|
|
|
|
|
|
|
У |
|
|
проверочную часть V из m n k символов. Порождающая матрица такого |
||||||||||
систематического кода будет иметь вид |
|
|
|
|
|
|||||
|
1 |
0 |
0 |
g0,0 |
g0,1 |
|
g0,n 1 |
|
|
|
|
|
|
|
|
|
|
Г |
|
|
|
|
G Ik P 0 |
1 |
0 |
g1,0 |
g1,1 |
|
g1,n 1 |
. |
|
(7.4) |
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
gk 1,0 |
gk 1,1 |
|
gk 1,n 1 |
|
|
||
|
0 |
0 |
0 1 |
|
|
|
|
|||
|
|
|
|
|
а |
|
|
|
|
|
7.5. |
Древовидные коды |
к |
|
|
|
|
|
|||
Древовидные |
|
е |
|
|
мгновенные значения состо- |
|||||
– э о коды, у которых |
||||||||||
яния кодера и послед ва |
ельные их изменения полностью описываются дре- |
вовидной диаграмм й. К |
дертсвѐрточного кода является устройством с памя- |
тью, на вход которогокодыпоступают наборы из k0 входных символов, а на вы- |
|
ходе появ яются наборы из n0 выходных символов, которые зависят как от |
||
|
|
и |
набора входных символов k0 , так и от v предыдущих входных символов. Па- |
||
|
л |
|
мять кодера хранит K k0 v входных информационных символов. Пара- |
||
метр K называют длиной кодового ограничения. |
||
б |
|
|
Параметры древовидного кода: скорость кода R k0 / n0 , свободное |
||
и |
|
|
кодовое расстояние dсв . |
||
БРассмотрим пример кодера древовидного типа. Он представляет ре- |
||
гистр сдвига с одним или несколькими сумматорами (рис. 7.1). |
||
Древовидная диаграмма этого кода приведена на рис. 7.2. Вертикальные линии диаграммы называются ребрами дерева, горизонтальные – ветвями. Каждое ребро дерева соответствует входному символу кодера, каждая ветвь представляет собой последовательность, состоящую из n0 кодирован-
98
ных (выходных) двоичных символов. Для рассматриваемого примера k0 1 и n0 2 . Процедура кодирования может быть описана последовательно во
времени. Входной бит 0 соответствует верхнему ребру, бит 1 – нижнему. На рис. 7.2 вершина каждой ветви (узел) обозначена числами от 0 до 3 (в двоичном представлении) в соответствии с содержимым двух левых ячеек регистра. Число означает состояние кодера. Ребра, выходящие из двух узлов, характеризуемых одинаковым состоянием, тождественны. Проследим, как формируется кодовая (выходная) последовательность символов на примере некоторой произвольной (входной) последовательности информационных бит.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Р |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Г |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Б |
1 |
|
П Выход |
|||||
|
|
|
X0 |
|
|
|
|
|
|
|
|
X1 |
|
|
|
|
|
|
X2 |
|
|
2 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
10110 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
к |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
Рис. 7.1. |
т |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
двоичного древовидного кода |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
Кодер |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
с параме рами R = 1/2, v = 2, K = 3 |
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
времени |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Пусть последовательн сть информационных бит имеет вид 10110. В |
||||||||||||||||||||||||||||||
|
|
|
л |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
начальный момент |
|
|
|
|
состояние кодера 000, на вход кодера подается |
||||||||||||||||||||||||||
|
|
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
первый бит (1), происходит движение по нижнему ребру, на выход подается ветвь (11). На вход кодера подается второй бит (0) происходит движение по верхнему ре ру, на выход подается ветвь (01). Третий бит (1) вызывает дви-
жен е по н жнему ребру, на выход подается ветвь (00) и т. д. Таким обра-
БПуть формирования ходовой последовательности выделен на рис. 7.2 жирной ломаной линией.
зом, нформационной последовательности бит (10110) соответствует кодовая |
|
последовательностьи |
символов (1101001010). |
7.6.Кодирование методом укрупнения алфавита
Данный метод передачи часто относят к методам m-ичной модуляции. Примером такой модуляции является широко используемая на практике мно-
99
гопозиционная ЧМ. Однако с полным основанием его относят и к методам кодирования блоковыми кодами (m-ичное кодирование). При m такое кодирование позволяет сколь угодно близко приблизиться к пределу Шенно-
на: Eb / N0 ln 2 .
Операция кодирования состоит в отображении блока из k последовательных независимых символов в один из m 2k подлежащих передаче сигналов, т. е. происходит переход от передачи символов двоичного алфавита к передаче символов (кодовых слов) m -ичного алфавита. Причем символы m - ичного алфавита должны приниматься в целом.
При анализе помехоустойчивости при кодировании укрупнением алфа-
бита, что ведет к повышению помехоустойчивости; Р
вита необходимо учитывать следующее:
– энергия символа укрупненного алфавита Em в k раз больше энергии
вместо передаваемого символа 1(0) можно принять только Иему альтернативный 0(1). При равновероятной передаче одного из символов m -ичного ал-
фавита ошибка может привести к приему с равнойГвероятностьюУ любого из ( m –1) оставшихся символов, что снизит помехоустойчивость системы.
– при использовании двоичных сигналов ошибка приведет к тому, что
Реализовано такое кодирование может быть с помощью ортогональных сигналов. Для этих целей могут быть применены различные алгоритмы по-
строения ансамблей ортогональных сигн лов. Второй путь – это использова- |
|||||||
|
|
|
|
|
|
|
Б |
ние симплексных сигналов. |
|
|
|
|
|||
Если используется некогерентный прием, т. е. параметры ЭС на прием- |
|||||||
|
|
|
|
|
|
а |
|
ной стороне заранее неизвестны и вычисляются статистически, то оптималь- |
|||||||
|
|
|
|
|
к |
|
|
|
|
|
|
е |
|
|
|
|
|
|
т |
|
|
|
|
ным является использование ортогональных сигналов. |
|||||||
Так же, как и при когерен ном приеме, с увеличением m требуемое для |
|||||||
|
|
вероя |
нос и ошибки отношение Eб / N0 ln 2 , при этом |
||||
обеспечения заданной |
|
||||||
потери полезного сигнала сущес венно меньше. |
|||||||
|
и |
|
|
|
|
|
|
|
л |
|
е алгебраических структур |
||||
7.7. Опреде ен |
|||||||
Важными и многочисленным классом часто используемых на практике |
|||||||
и |
|
|
|
|
|
|
|
блоковых кодов являются циклические коды. Поиск лучших среди блоковых |
|||||||
Б |
|
|
|
|
|
|
|
кодов, тб. е. таких, которые при прочих равных условиях (одинаковых n и k )
обнаруж вают или/и исправляют наибольшее количество ошибок, связан с введением некоторых ограничений на их свойства или алгоритмы их построения. Кроме того, сами алгоритмы кодирования и декодирования включают алгебраические операции суммирования и умножения. Эти алгебраические операции выполняются в соответствии с правилами определения алгебраических структур, которые имеют символы, содержащиеся в кодовых словах. Далее приводится минимальная информация для определения алгебраических структур, необходимая для изучения блоковых кодов и алгоритмов их декодирования.
100

|
|
|
|
|
|
|
Верхнее поддерево |
00 |
|
|
00 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
00 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
|
01 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
00 |
|
|
|
10 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
01 |
|
11 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
00 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
11 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
10 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
Ветвь |
|
|
|
|
|
|
1 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
01 |
|
|
|||||
|
|
|
|
|
00 |
|
|
|
|
|
|
|
3 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
|
00 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
01 |
|
|
|
11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
00 |
|
01 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
И |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|||
|
|
|
Ребро 0 |
|
|
|
|
11 |
|
|
|
10 |
1 |
|
11 |
|
Р |
||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
00 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
2 |
|
У |
||
|
|
|
|
|
|
|
|
|
|
|
|
3 |
01 |
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
01 |
|
|
|
Вход |
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
Г |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
Нижнее поддерево |
|
00 |
00 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
а |
|
|
11 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
11 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
к |
|
11 |
|
01 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|||||||
|
|
|
|
|
|
|
|
01 |
|
|
|
|
1 |
|
10 |
|
|
||
|
|
|
Ребро 1 |
|
|
е |
|
|
|
|
01 |
|
|
11 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
00 |
|
|
|
|
|
|
|
|
т |
|
|
|
|
|
00 |
|
10 |
2 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
01 |
|
|
|||
|
|
|
|
|
|
|
11 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
00 |
|
|
||
|
|
|
о |
|
|
1 |
|
|
|
|
|
11 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
11 |
|
|
|||||
|
|
|
|
Узел |
|
|
|
|
|
10 |
|
|
|
11 |
|
|
|||
|
и |
|
|
|
|
|
|
|
|
0 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
00 |
|
01 |
|
|
|||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
л |
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
||||
|
|
|
|
|
|
|
10 |
|
|
|
|
1 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
1 |
|
|
10 |
3 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
00 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
01 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
01 |
|
10 |
|
|
||
и |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
01 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Р с. 7.2.бЧасть полубесконечного дерева для двоичного древовидного кода с параметрами R = 1/2, v = 2, K=3
Группой G называют множество элементов или символов, для которых определена одна операция (сложение или умножение) и выполняются следующие аксиомы:
– операция может быть применена к двум другим элементам группы, в результате чего получается третий элемент этой же группы;
101
– для любых трех элементов a , b , c справедливо следующее:
( a b ) c a ( b c ) и ( ab )c a( bc ) ;
–в группе существует единственный (нейтральный) единичный элемент. Для сложения: a 0 0 a a . Для умножения:1a a1;
–каждый элемент группы имеет единственный обратный элемент: a ( a ) ( a ) a 0 . aa 1 a 1a 1;
–если a b b a и ab ba , то такая группа называется абелевой. Кольцом R называют множество элементов или символов, для которых
определены две операции: сложения – ( a b ) и умножения – ab . |
Р |
|||||||
Должны выполняться также следующие аксиомы: |
|
|
||||||
|
|
|
||||||
– множество R |
является аддитивной абелевой группой относительно |
|||||||
операции сложения; |
|
|
|
|
|
И |
||
|
|
|
|
|
|
|
|
|
– для любых a и b из множества R ab ba |
также является элементом R ; |
|||||||
|
|
|
|
|
У |
|
||
– для любых a |
b и c |
из множества R a( bc ) ( ab )c |
также является |
|||||
элементом R ; |
|
|
|
Г |
|
|
|
|
|
|
|
|
|
|
|
||
– для любых |
a b и |
c из множества |
R справедливы равенства: |
|||||
a( b c ) ab ac и ( b c )a ba ca . |
Б |
|
|
|
|
|||
|
|
|
|
|
|
|||
Полем F называют множество элементов, в котором определены две операции – сложение и умножение, причем это множество по операции сложения образует аддитивную абелеву группу с единичным элементом, обо-
значенным «0»; по операции умножения группу образуют все элементы поля, |
||||
кроме 0, единичный элемент этой группы обозн чается «1». |
||||
Для любого числа |
|
а |
||
q , являющ гося степенью простого числа, суще- |
||||
|
|
|
|
к |
ствует поле, содержащее q эл м нтов. Поля с конечным числом элементов |
||||
q pi , где p – простое число, еа i – любое натуральное число, называют по- |
||||
лями Галуа и обозначаю ся GP(q). |
|
|||
При i 1 элементами поля будут простые натуральные числа от 0 до |
||||
|
|
|
т |
|
p –1, и операц сл жен я и умножения над этими числами производятся по |
||||
|
|
о |
|
|
mod2. Такие по я Га уа называются простыми. При i 1 поля Галуа являют- |
||||
ся расширением простого поля. |
|
|||
|
и |
|
|
|
л |
|
|
|
|
7.8. Циклические коды |
|
|||
б |
|
|
|
|
иЦиклическим кодом называют такой блоковый код, которому вместе с |
||||
Бнекоторым кодовым словом принадлежат и другие кодовые слова, являющиеся всеми его циклическими сдвигами. Пусть B = [bn-1bn-2…b1b0] – кодовое слово. Тогда последовательность B(1) = [bn-2b1…b0bn-1], являющаяся циклическим сдвигом B , также является кодовым словом данного циклического кода.
При операциях с циклическими кодами обычное кодовое слово B удобно представлять в виде многочлена B( X ) со степенью n 1, где коэф-
фициенты при степенях переменной величины есть символы кодового слова.
102
B( X ) b |
|
|
X n 1 b |
|
X n 2 ... b X b . |
|
(7.5) |
|||||||||||
|
n 1 |
|
|
|
n 2 |
|
|
|
1 |
|
|
0 |
|
|
|
|||
Коэффициенты B( X ) |
есть |
|
элементы |
поля Галуа. Многочлен B(1 ) |
||||||||||||||
можно получить умножением многочлена B( X ) на X , т. е. это остаток от |
||||||||||||||||||
деления |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[ XB( X )] на X n 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
По аналогии |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B( i )( X ) X i B( X ) /( X n |
1). |
|
|
|
|
|
|
(7.6) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Р |
|
Представим также информационное сообщение в виде |
И |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
C( X ) c |
k 1 |
X k 1 |
|
c |
k 2 |
X k 2 |
... c X c |
, |
|
|
(7.7) |
|||||||
|
|
|
|
|
|
|
|
1 |
|
|
0 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
Г |
|
|
|
|
|||
где последовательность C [ ck 1 ,ck 2 ,...,c1 ,c0 |
] – информационные символы. |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
||
Введем некоторый порождающий многочлен, который является одним |
||||||||||||||||||
из сомножителей при разложении |
X n 1 |
|
множители. |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
на |
|
|
|
|
|
|
|
|
|||
g( X ) X |
nкk |
|
n k 1 |
... g1 X |
1. |
(7.8) |
||||||||||||
|
gn k 1 X |
|
||||||||||||||||
|
|
|
|
е |
|
|
|
|
|
|
|
|
|
|
|
|||
При практическ м п с роении |
двоичных циклических |
кодов ( n,k ) |
||||||||||||||||
и выборе порождающих мн г членов можно воспользоваться специальной |
||||
таблицей. |
|
|
т |
|
|
о |
|
||
|
|
|
||
Можно зап сать без вывода: |
|
|||
|
и |
Bi (X ) Ci (X )g(X ) , |
|
|
|
л |
|
(7.9) |
|
|
|
|
|
|
|
k |
|
|
|
где i 0,1б, ...q . |
|
|
|
|
Порождающий многочлен g( X ) является делителем двухчлена |
X n 1 |
|||
и |
|
|
|
|
. Следовательно, справедливо равенство |
|
|||
Б |
|
|
|
|
|
|
X 2 1 g( X )h( X ) . |
(7.10) |
|
Функцию h( X ) называют проверочным многочленом.
В ряде случаев при реализации кодера циклического кода на основе регистра сдвига пользуются проверочным многочленом h( X ) . Этот многочлен
103
также используют при построении декодеров для декодирования последовательностей, построенных по мажоритарным алгоритмам. В этом случае на основе проверочного многочлена h( X ) формируется n k проверочных со-
отношений:
k |
|
S j k hib j i , k j n 1. |
(7.11) |
i 0 |
|
Соотношение (7.11) называют синдромом комбинаций Bi . Равенство нулю выражения (7.11) имеет место только в том случае, если коэффициенты bij являются коэффициентами проверочного многочлена. Это означает, если
координаты синдрома S равны нулю, то для этих символов bij не искажены
помехами. |
Р |
|
|
|
И |
7.9. Наиболее распространенные циклические коды |
||||||||||||||||||||||||||||||||||||||||||||||
Коды Хемминга могут быть как двоичными, так и недвоичными. Дво- |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
|
|
|||||
ичные коды Хемминга – это совершенные циклическиеУкоды с параметрами |
||||||||||||||||||||||||||||||||||||||||||||||
n 2l 1 , |
k 2l l 1, d 3 . |
Данные коды исправляютГтолько одиночные |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
|
|
|
||||||||||
ошибки. При l 3 |
|
g( X ) X 3 X 1 |
|
и |
h(X) X3 |
X2 |
|
X 1 кодер кода |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
к |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Хемминга (7.4) на основе порождающего и проверочного многочленов пред- |
||||||||||||||||||||||||||||||||||||||||||||||
ставлен на рис. 7.3. |
|
|
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
+ |
П1 |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
П2 Выход |
||||||||||
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вход 0101 |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
л |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Многочлен сообщения |
|
|
|
|
|
|
|
|
|
|||||||||||||||
и |
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б) |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Б |
|
П1 |
|
|
|
|
0 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
Выход |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Кодовое слово |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
Вход |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
0110 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
Рис. 7.3. Кодер на основе многочленов: |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
а – порождающего; б – проверочного |
|
|
|
|
|
|
||||||||||||||||||||||||||||||
Изменения состояний регистра кодера для порождающего многочлена представлены в табличном виде ниже. В исходном состоянии в регистре – все нули.
104

Информация |
Номер шага |
Содержимое регистра |
0 |
1 |
000 |
1 |
2 |
110 |
1 |
3 |
101 |
0 |
4 |
100 |
Код Голея – двоичный совершенный циклический код с параметрами n = 23, k = 12 и d = 7.
Порождающий многочлен:
|
|
|
g( X ) X 11 X 9 X 7 X 6 X 5 X 1. |
|
Р |
||||||||
|
Проверочный многочлен |
|
|
|
|
|
|
|
|||||
|
|
h( X ) X 12 X 10 X 7 X 4 X 3 X 2 X 1 |
|||||||||||
реализуется |
|
|
|
|
|
|
|
|
|
|
И |
||
на основе регистров сдвига. Пример реализации кода приведен |
|||||||||||||
на рис. 7.4. |
|
|
|
|
|
|
|
|
У |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
Г |
|
|
||
Вход |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
10 |
11 |
12 |
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
|
|
Рис. 7.4. Р ализацияода Голея |
|
|
|
Кодовое |
|||||
|
|
|
|
|
|
|
слово |
||||||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
к |
|
|
|
|
|
|
|
|
Коды Боуза–Чоудхури–Хоквинг ма (БЧХ) |
|
|
|
|
|
|||||||
|
Для любых целых чисел m и t ( n / 2 ) |
существует двоичный код БЧХ |
|||||||||||
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
длиной n 2m 1, исправляющий все комбинации из t |
0 |
и меньшего числа |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ошибок и содержащий не б лее mt0 проверочных символов в каждом слове. |
|||
|
|
|
т |
Порождающ е многочлены БЧХ-кодов представляют собой НОК ми- |
|||
|
|
о |
|
нимальных многоч енов |
m ( X ) делителей двучлена X 2m 1 1: |
||
|
|
и |
i |
|
|
|
|
g( X ) лНОК m1( X )m3( X )...M 2t0 1 . |
|||
|
б |
|
|
Коды БЧХ – квазисовершенные коды, т. е. лучшие из двоичных кодов. |
|||
и |
|
|
|
Коды Рида–Соломона |
|||
Составляют подкласс недвоичных БЧХ-кодов. Параметры РС-кодов: |
|||
Б |
|
|
|
– длина кодового |
слова N q 1 ( 2k 1) q -ичных символов, где |
||
k 1,2,3,...,n 1;
– количество информационных символов в кодовом слове K N 2t ;
– минимальное кодовое расстояние dmin N K 1;
– кодовая скорость R K / N ;
105
|
|
– количество |
исправляемых ошибок в кодовом слове t, |
|||||
|
1 |
|
|
|
|
1 |
|
|
t |
|
(Dmin |
1) |
|
|
|
(N K ) . |
|
|
2 |
|||||||
2 |
|
|
|
|
|
|
||
Эти коды позволяют исправлять все ошибки, группирующиеся в пачки длиной не более t q -ичных символов.
7.10. Мажоритарно декодируемые коды
В основе функционирования этих кодов лежит одно правило – правило
стоит в том, что ни один из символов кодового слова не долженРвходить в систему составленных уравнений два и более раз. При этом при декодирова-
ортогональных проверок. Для каждого символа произвольного кодового сло-
ва выполняется проверка с помощью многочлена h( X ) . Суть проверки со-
нии вычисляется синдром и составляется таблица соответствия синдромов |
|||
|
|
|
И |
образцам исправляемых ошибок. Если синдром равен нулю, то символ пере- |
|||
дан правильно. |
|
У |
|
|
|
||
|
Г |
|
|
7.11. Декодирование циклических кодов |
|
|
|
|
Б |
|
|
Методы декодирования цикличес их одов разделяются на два больших |
|||
класса: алгебраические и неалгебраичес ие. В основе алгебраических методов |
|
|
а |
к |
|
е |
|
лежит решение систем уравнений, опр д ляющих места расположения и значе-
ния ошибок. При неалгебраич ских м тодах та же цель достигается с использо-
ванием известных струк урных поня ий и свойств кодов, позволяющих опреде-
лить места и значения тех же ошибок более простыми путями. Среди алгорит-
мов жесткого декодир вания выделяют алгоритм табличного декодирования по |
|||
минимуму расстоян я. Рассмтрим данный алгоритм на примере блокового ко- |
|||
да (5.2). Данный код |
образует четыре кодовых слова: |
||
00000 |
01011 |
10101 |
11110. |
|
и |
|
|
В этих с овах первые два символа информационные, три последую- |
|||
щих – проверочные. Минимальное кодовое расстояние между кодовыми сло- |
||
вами dmin |
л |
|
3 , следовательно, может быть исправлена любая, произвольно |
||
|
б |
|
расположенная одиночная ошибка. В табл. 7.1 показан принцип табличного |
||
и |
|
|
Б |
|
|
декодирования блокового кода. В столбцах расположены двоичные пятиразрядные комбинации, имеющие меньшее расстояние Хемминга до кодового слова, образующего данный столбец, чем до кодовых слов, образующих другие столбцы.
Если принята комбинация, принадлежащая первому столбцу, она отождествляется с кодовым словом 00000 и декодируется как 00.
Технически кодер реализуется в виде запоминающего устройства, по адресам которого записаны следующие комбинации: для первого столбца – 00; для второго – 01; для третьего – 10; для четвертого – 11. Современные
106

микросхемы памяти позволяют строить табличные декодеры для кодов с n < (15–20). Приведенный алгоритм является алгоритмом декодирования по минимальному расстоянию Хемминга, т. е. алгоритомом максимального правдоподобия для ДСК.
Синдромное декодирование является достаточно простым методом жесткого декодирования циклических кодов. Рассмотрим данный алгоритм в общем виде. Для всех вариантов исправляемых выбранным кодом ошибок вычисляются синдромы и составляется таблица соответствия синдромов образцам исправляемых ошибок. При этом под синдромом понимается следующее. Если вектор S определяется координатами S j k , то такой вектор
называют синдромом комбинации B j .
|
|
|
k |
|
|
|
|
|
|
|
|
|
Р |
||
|
S j k hibj i 0, |
при k j n 1. |
|
|
|||||||||||
|
|
И |
(7.12) |
||||||||||||
|
|
|
i 0 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
Таблица 7.1 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
У |
|
|
|
|
|
Табличное декодирование блокового кода |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
Г |
|
|
|
|
|||
№ п/п |
|
|
|
Кодовые слова |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
00000 |
|
01011 |
|
|
Б |
|
|
11110 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
10101 |
|
|
|
|
|
||||||
1 |
00001 |
|
01010 |
|
|
10100 |
|
|
11111 |
|
|
|
|||
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
|
|
2 |
00010 |
|
01001 |
|
|
10111 |
|
|
11100 |
|
|
|
|||
|
|
|
|
|
к |
|
|
|
|
|
|
|
|
||
3 |
00100 |
|
01111 |
|
|
10001 |
|
|
11010 |
|
|
|
|||
|
|
|
|
е |
|
|
|
|
|
|
|
|
|
||
4 |
01000 |
|
00011 |
|
|
11101 |
|
|
10110 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
5 |
10000 |
|
11011 |
|
|
00101 |
|
|
01110 |
|
|
|
|||
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
|
|
6 |
11000 |
|
10011 |
|
|
01101 |
|
|
00110 |
|
|
|
|||
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
||
7 |
10010 |
|
11001 |
|
|
00111 |
|
|
01100 |
|
|
|
|||
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
приведенал |
таблица соответствия синдромов. Если код цикличе- |
||||||||||||||
ния r( X ) , имеющий степень, меньшую, чем
ский, то с ндром вычисляется с помощью регистров сдвига путем деления |
|
|
б |
комб нац в виде многочлена B( X ) на многочлен g( X ). Остаток от деле- |
|
Ниже |
|
Б |
|
S( X ) . Дальнейшие операции по декодированию выполняются с помощью
запоминающего устройства, адресами которого являются синдромы, а в информационной части хранятся соответствующие им векторы ошибок. Далее, сложив принятую комбинацию и вычисленный вектор ошибок, определяем наиболее вероятно принятое слово и соответствующий ему блок информационных символов.
107
|
|
|
|
|
|
Таблица 7.2 |
|
|
||
|
Соответствие синдромов |
|
|
|
|
|||||
|
|
|
|
|
|
|
||||
|
№ п/п |
Вектор ошибки |
Синдром |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
00000 |
|
000 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
00001 |
|
001 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
00010 |
|
010 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
00100 |
|
100 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
01000 |
|
011 |
|
|
|
Р |
|
|
|
|
|
|
|
|
|
|
||
|
6 |
|
10000 |
|
101 |
|
|
|
||
|
|
|
|
|
|
|
|
|
||
|
7 |
|
11000 |
|
110 |
|
|
|
||
|
|
|
|
|
|
|
|
|
||
|
8 |
|
10010 |
|
111 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
|
|
|
|
|
|
|
|
|
|
||
7.12. Сверточные коды |
|
|
|
У |
|
|||||
|
|
|
|
|
|
|
|
|||
Сверточный код в отличие от блочного описывается тремя целыми |
||||||||||
|
|
|
|
|
|
Г |
|
|
||
числами – n , k , K . Отношение k / n имеет тот же смысл, что и для блочных |
||||||||||
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
кодов, однако n не определяет длину кодового слова или блока. Целое число |
||||||||||
|
|
|
|
к |
|
|
|
|
|
|
K указывает число разрядов |
k -кортежа в одирующем регистре сдвига. Его |
|||||||||
|
|
|
е |
|
|
|
|
|
|
|
называют длиной кодового ограничения. Важная особенность сверточных |
||||||||||
кодов состоит в том, что код р им |
т память – n -кортежи, получаемые в ре- |
|||||||||
|
т |
|
|
|
|
|
|
|
||
зультате кодирования, являются |
функцией |
не только одного входного |
||||||||
k-кортежа, но и предыдущих |
K 1 входных k-кортежей. |
|
|
|||||||
|
о |
|
|
|
|
|
|
|
|
|
После кодирования каждое кодовое слово состоит из двоичных кодо- |
||||||||||
вых символов, называемых канальными символами, канальными битами, или
битами кода. В отл ч е |
битов входного сообщения кодовые символы не |
являются незав с |
. |
Обычный сверточный кодер показан на рис. 7.5. Он реализован на |
|
К-разрядном регистремымисдвига с n сумматорами по модулю 2, где К – длина |
|
кодового ограничения – количество k -битовых сдвигов, после которых один |
|
л |
|
информац онный бит может повлиять на выходной сигнал кодера. В каждый |
|
момент бвремени на место первых k |
разрядов перемещаются k новых бит; |
все б ты в регистре смещаются на k |
разрядов вправо, и выходные данные n |
и |
|
сумматоров последовательно дискретизируются, формируя выходной код. |
|
Б |
|
108
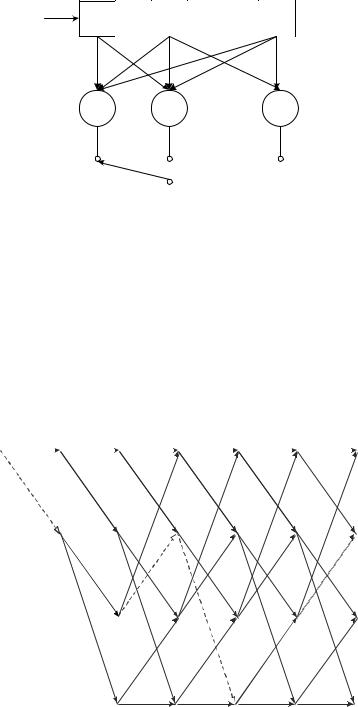
Входная |
1 |
2 |
3 |
kK |
|
последовательность m |
|||||
|
|
|
|
||
|
|
` |
|
|
|
|
+ |
|
+ |
+ |
kK- разрядный регистр сдвига
n сумматоров по модулю2
|
|
|
|
Р |
Последовательность |
|
|
|
|
кодового слова U |
|
И |
||
|
|
|
||
Рис. 7.5. Сверточный кодер с длиной кодового ограничения К |
||||
и степенью кодирования k/n |
У |
|
||
|
|
|
||
Вторым примером сверточного кодера является кодер, изображенный |
||||
|
Г |
|
|
|
на рис. 7.1, и древовидная диаграмма кода, изображенная на рис. 7.2. Для рассматриваемого сверточного кода решетчатая диаграмма приведена на рис. 7.6.
|
Ветви |
|
|
|
|
|
а |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
00 |
|
00 |
|
00 |
|
|
00 |
|
|
00 |
00 |
|
0 = (00) |
|
|
|
|
|
к |
|
Б |
|
|
|||||
|
|
|
|
е |
|
|
|
|
|
|
|||||
|
|
|
|
11 |
|
11 |
|
|
|
11 |
11 |
11 |
|||
|
|
|
|
|
11 |
|
|
|
|
||||||
1 = (10) |
|
|
т |
11 |
|
|
11 |
|
|
11 |
11 |
|
|||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
о |
|
|
00 |
|
|
|
00 |
00 |
00 |
|||
|
|
|
01 |
|
01 |
|
|
01 |
01 |
01 |
|
||||
|
и |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
2 = (01) |
|
|
|
10 |
|
10 |
|
10 |
|
|
10 |
10 |
|
||
л |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
б |
|
|
|
|
|
|
10 |
|
|
10 |
|
10 |
10 |
|
|
3 = (11) |
|
|
|
|
|
01 |
|
|
01 |
|
|
01 |
01 |
|
|
БЛинииЛ нии узлов
Рис. 7.6. Решетчатая диаграмма сверточного кода
узлов решетки представляют состояние регистра: 0 = (00), 1 = (10), 2 = (01), 3 = (11). Для рассматриваемого кода имеется четыре линии узлов. На рисунке сплошная линия перехода из одного узла в другой соответствует ветви (двум выходным символам), генерируемой после поступления входного бита), а штриховая – ветви, которая генерируется при поступлении входного бита 1.
В структуре решетчатой диаграммы, как и в структуре древовидной, имеет место периодичность повторения состояния после достижения глубины ветвления K (в нашем случае K 3). Так, из узла 0: при входном бите 0
109
происходит переход в узел 0, при этом на выходе кодера генерируется ветвь 00; при входном бите 1 происходит переход в узел 1, при этом на выходе кодера генерируется ветвь 11. Из узла 1: при входном бите 0 происходит переход в узел 2, при этом проходит ветвь 01; при входном бите 1 происходит переход в узел 3, при этом генерируется ветвь 10.
Путь на решетчатой диаграмме при исходном состоянии регистра 000 и входной последовательности 10110 отмечен жирной линией. Вышеназванной входной последовательности соответствует последовательность кодированных символов 1101001010.
Решетчатая диаграмма, как и древовидная, однозначно связывает информационную последовательность бит, последовательность состояний ко-
пороговое декодирование, декодирование по алгоритму ВитербиРи последовательное декодирование. Пороговое декодирование не нашло широкого
дера и последовательность кодированных символов на его выходе.
Известны три основных алгоритма декодирования сверточных кодов:
практического применения, хотя его модификация как многопороговое деко- |
|
|
И |
дирование позволяет получить существенный энергетический выигрыш. |
|
При декодировании по Витерби каждой последовательности информа- |
|
У |
|
ционных бит соответствует свой путь на решетчатой диаграмме выбранного |
|
Г |
|
кода. Задача декодера сверточного кода, реализующего алгоритм Витерби, |
|
сводится к тому, чтобы найти на решетч той Бдиаграмме разрешенный путь, наиболее близкий по какой-либо приемлемой метрике к пути, соответствую-
щему принятому на фоне помех последов тельности кодированных символов |
|
|
а |
и по нему принять решения о знач нии переданных информационных бит. |
|
Поскольку здесь анализируются |
кразрешенные пути и в результате анали- |
за выбирается путь с минимальнойтвсем трикой как наиболее правдоподобный,
то решающий указанную задачу декодер (декодер Витерби) является декодером максимального правд п добия.
|
и |
|
Существует неск |
реализаций алгоритмов последовательного де- |
|
кодирования сверт чных |
д в. Наиболее широкое применение в системах |
|
связи нашел а гор тмлькопоследовательного декодирования, предложений Фано |
||
б |
|
|
еще до появ ения а горитма Витерби. В отличие от декодера Витерби, этот |
||
алгоритм при приемлемой сложности реализации позволяет декодировать |
||
|
при |
|
сверточные лкоды с длиной кодового ограничения K 9 . Алгоритм Фано |
||
позволяет декодировать и коды со значениями K 9 , но поскольку он не яв- |
||
Б |
|
|
ляется алгоритмом максимального правдоподобия, то по помехоустойчиво- |
||
сти |
|
прочих равных условиях уступает алгоритму Витерби. |
|
В отличие от алгоритма Витерби, где на каждом шаге производится |
|
обновление метрик всех выживших путей, в алгоритме Фано обновляется метрика только того пути, который оценивается как наиболее вероятный. Такой подход к декодированию может рассматриваться как метод проб и ошибок для поиска правильного пути на диаграмме. Поиск осуществляется последовательно, так что в каждый момент времени происходит формирование только одного пути. Декодер может двигаться по выбранному пути вперед или назад и менять предыдущие решения. Однако основное правило при реа-
110
лизации алгоритма последовательного декодирования состоит в том, что декодер не должен двигаться ни вперед, ни назад по пути, достоверность которого ниже некоторого текущего порога. Все разрешенные переходы, исходящие из текущего узла, должны сравниваться с принятой ветвью и упорядочиваться в соответствии с их вероятностью. Декодер «движется» по наиболее вероятному пути из каждого узла до тех пор, пока значение его достоверности превышает значение текущего порога.
7.13. Основные принципы каскадного кодирования
дефиците энергетики радиолиний и т.д.). Применение в таких случаяхРболее длинных блоковых или сверточных кодов приводит к недопустимому услож-
На практике нередко возникают задачи, когда необходимо использо-
вать наиболее мощные коды (обеспечение высокой помехоустойчивости при
нению самого декодера. Форни предложил схему каскадного (многоуровне- |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
||
вого) кодирования. На практике наиболее широко используют двухуровне- |
||||||||||||||||||||||||||||||
вую схему. Структурная |
схема двухуровневого |
каскадного кодирования |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
|||||||
представлена на рис. 7.7. |
|
|
|
|
|
|
|
|
|
|
|
|
|
Г |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Ввод информации |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
Выход информации |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
PC (N,K) |
|
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
Внешний |
|
|
|
Внутренний |
N* |
|
|
|
|
|
|
N* |
|
Внутренний |
|
|
|
|
Внешний |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
ксвязи |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
кодер |
|
|
|
|
кодер |
|
|
е |
|
|
|
|
|
декодер |
|
|
|
|
|
декодер |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Цифровой канал |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Орт г нальный (2k,k) |
|
|
|
|
|
|
|
|
|
Мягкое |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
ли |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
т |
|
|
|
|
|
|
декодирование |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
сверт чный (n,k) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Помехи |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
Рис. 7.7. Схема двухуровневого каскадного кодирования |
|||||||||||||||||||||||||||
|
|
|
л |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Здесь спользуются |
два |
|
кода: внешний |
код, |
обычно блоковый |
||||||||||||||||||||||||
|
|
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ся q -ичный код ( q 2 ) Рида–Соломона. Такие коды имеют максимальное
и недво чный, и внутренний. В качестве внешних кодов обычно используют- |
|
и |
k |
Б |
|
кодовое расстояние для фиксированных N и K и относительно просто декодируются. В качестве внутренних кодов используются циклические, ортогональные и сверточные коды.
Перед кодированием внешним кодом двоичная информация разбивается на последовательные группы по k символов каждая. Такая группа представляет собой один q -ичный символ. Далее последовательности из K q -
ичных символов кодером ставится в соответствие кодовое слов РС-кода дли-
111
ной N q -ичных символов или длиной N k двоичных символов. Далее со-
общение кодируется внутренним кодом.
При использовании внутреннего кодирования каждой указанной выше группе k двоичных символов ставится в соответствие кодовое слово внутреннего кода длиной n двоичных символов. Длина полученного кодового
слова каскадного кода будет равна N* N n двоичных символов; количество информационных бит – K* Kk , скорость каскадного кода будет равна
R* R |
/ R |
Kk / Nn . |
(7.13) |
|
внешний |
внутр |
|
Р |
|
|
|
|
m - |
|
При использовании в качестве внутренних кодов ортогональных |
||||
|
|
|
И |
|
ичных кодов каждой указанной выше группе из k двоичных символов ставится в соответствие кодовое слово ортогональных m -ичных кодов. Так как при использовании ортогональных m -ичных кодов требования к полосе про-
|
|
|
|
|
|
|
|
|
|
|
Г |
|
|
пускания растут пропорционально m , то и применение таких кодов возмож- |
|||||||||||||
но только в том случае, когда имеется запас по полосе пропускания. |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
При использовании сверточных кодов РС длина Уполученного кодового |
||||||||||||
слова каскадного кода будет равна N* Nn |
0 |
, |
количество информационных |
||||||||||
бит составит K* |
Kk |
|
|
|
а |
|
|
|
|||||
|
|
|
|
0 |
|
к |
|
|
|
|
|
|
|
|
|
|
|
|
R* R |
Kk / Nn . |
|
||||||
|
|
|
|
|
/ R |
(7.14) |
|||||||
|
|
|
|
|
внешний |
внутр |
|
|
|
0 |
0 |
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
Декодирование информации осущ ствляется в обратном порядке. |
|
|||||||||||
|
Разработка |
турбокодов явилась заметным достижением в теории и тех- |
|||||||||||
|
7.14. Сверточные урбокоды |
|
|
|
|
|
|
|
|||||
|
|
л |
|
|
|
|
|
|
|
|
|
|
|
нике помехоустойч вого кодирования, так как позволила вплотную прибли- |
|||||||||||||
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
зиться к преде уиШеннона. Для таких кодов получены следующие парамет- |
|||||||||||||
ры: |
при |
1/ 2 |
в канале связи с БГШ P |
|
|
10 5 требуется соотношение |
|||||||
R |
|
|
|||||||||||
|
|
|
|
|
|
|
|
ош |
|
|
|
||
Eb / N0 0,7 дБ, что на (1,5–2) дБ меньше, чем при использовании лучших
Бкаскадных кодов при R 1/ 2 .
Турбокоды бывают следующего вида:
– сверточные турбокоды (СТК), которые формируются путем параллельного соединения двух и более сверточных кодеров;
– блоковые турбокоды (БТК), которые формируются путем параллельного соединения двух и более блоковых кодеров.
Кодер эффективного СТК строится параллельным соединением двух или нескольких рекурсивных систематических сверточных кодов (РССК) с относительно небольшой длиной кодового слова – K 3 5 . Схема кодера представлена на рис. 7.8.
112

|
|
|
Информация |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
` |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
РССК 1 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
|
|
|
|
11 |
|
|
|
|
|
|
|
12 |
|
|
|
|
|
13 |
|
|
Р |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
` |
|
|
|
|
|
|
|
|
|
|
И |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Выход |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
|
|
||||
|
Перемежитель |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
РССК 2 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
X |
|
|
|
|
|
2 |
1 |
|
|
|
|
|
|
|
2 |
2 |
|
|
|
Г2 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
к |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
е |
X |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Рис. 7.8. Кодер систематич ского сверточного турбокода с К = 4 |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
символ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Каждый кодер РССК по умолчанию работает со скоростью R 1/ 2 . |
|||||||||||||||||||||||||||||||
Значение символа на |
|
|
|
стематическом выходе верхнего РССК совпадает со |
||||||||||||||||||||||||||||
ем записываетсялв матричную память и считывается из нее на вход нижнего
значением входного б та, а на втором выходе верхнего регистра формирует-
б |
|
ся проверочный |
. Для осуществления операции перемежения выделя- |
ется некоторый |
ок из k информационных бит, который перед кодировани- |
и |
k |
РССК по псевдослучайному закону. Систематический выход нижнего реги-
зультатеБна выходе получаем: последовательность a с систематического выхода верхнего регистра (она же совпадает с входной последовательностью) и последовательно два проверочных символа с верхнего xk и нижнего
стра не спользуется, а второй его выход формирует проверочный бит. В ре-
yk регистров. Кодовая скорость сформированной таким образом последова-
тельности будет равна R 1/ 3. Если проверочные символы снимать с регистров через такт (в одном такте – с первого, во втором – со второго), то скорость можно повысить до R 1/ 2 .
113
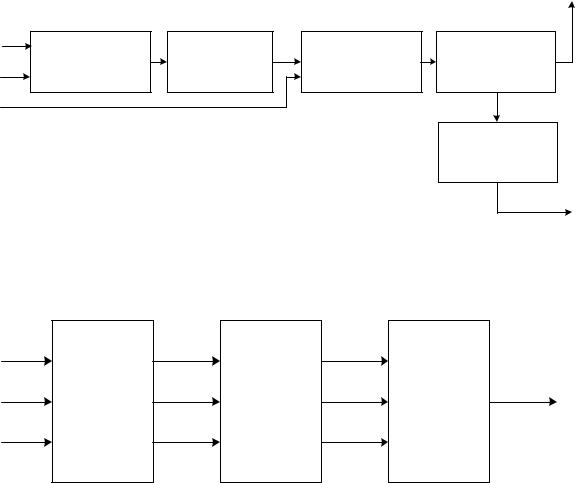
|
Анализ результатов экспериментальных исследований СТК показал, |
|||||||||||||
что структура перемежителя существенно не влияет на эффективность коди- |
||||||||||||||
рования. |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Декодер СТК, так же как и кодер, состоит из двух декодеров (рис. 7.9). |
|||||||||||||
|
В декодерах 1 и 2 используется алгоритм для учета особенностей ре- |
|||||||||||||
курсивных кодов. Это алгоритм работает на основе критерия максимальной |
||||||||||||||
апостериорной вероятности (Maximum A Posteriori) и позволяет формировать |
||||||||||||||
так называемые мягкие решения: мягкий вход – мягкий выход (Soft Input – |
||||||||||||||
Soft Output, SISO). Информация, полученная после декодирования вторым |
||||||||||||||
декодером, поступает на вход первого декодера, что повышает эффектив- |
||||||||||||||
ность декодирования. Таких операций может быть две–три. Таким образом, |
||||||||||||||
используется модульная конструкция декодера (рис. 7.10). |
|
Р |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
На следующую |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
итерацию |
ak |
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
xk |
SISO Декодер 1 |
Перемежитель |
|
SISO Декодер 2 |
УДеперемежитель |
|||||||||
yk |
|
|
|
|
|
|
|
|
|
|
Г |
|
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
Решающее |
||
|
|
|
|
|
|
|
|
|
а |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
устройство |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
к |
|
|
|
|
|
|
|
|
|
|
|
|
|
е |
|
|
|
|
|
Выход |
|
|
|
|
|
|
|
|
|
|
|
|
|
турбодекодера |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
Рис. 7.9. Схема декодера СТК (одна итерация) |
||||||||||
|
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
(ak)0 |
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
(ak)1 |
|
|
|
(ak)2 |
|
|
|
Декодированная |
||
|
|
|
|
и |
|
|
|
|
|
|
|
|
||
(xk)0 |
|
|
л |
(xk)1 |
Модуль 2 |
|
(xk)2 |
Модуль 3 |
информация |
|||||
|
|
|
|
|
|
|
|
|||||||
|
|
Модуль 1 |
|
|
|
|
|
|||||||
(yk)0 |
|
б |
|
(yk)1 |
|
|
|
(yk)2 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
и |
|
|
|
|
|
|
|
|
|
|
|
|
||
Б |
Рис. 7.10. Модульная схема итеративного декодера СТК |
|||||||||||||
|
|
|||||||||||||
114
7.15. Блоковые турбокоды |
|
|
|
|
|
|
|
|
|
|
||||||||
Блоковые турбокоды в сочетании с алгоритмом SISO с несколькими |
||||||||||||||||||
итерациями позволяют приблизиться к пределу Шеннона. БТК более эффек- |
||||||||||||||||||
тивны, |
чем сверточные при R 0,7 . БТК могут формироваться как последо- |
|||||||||||||||||
вательным, так и параллельным соединением двух или нескольких блоковых |
||||||||||||||||||
кодов. Последовательное построение блоковых кодов – турбокоды произве- |
||||||||||||||||||
дения (ТРС) – является более эффективным. Структура такого турбо-кода |
||||||||||||||||||
представлена на рис. 7.11. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
n1 |
|
|
|
|
|
|
Р |
|
|
|
|
|
|
|
k1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k2 |
|
|
|
Информационные биты |
|
|
|
Символы проверокИпо |
||||||||||
|
|
|
|
|
|
|
|
|
строкам |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
|
|
n2 |
|
|
|
|
|
|
|
|
|
|
|
|
Г |
|
||||
|
|
|
|
Символы проверок по |
|
|
Символы проверок проверочных |
|||||||||||
|
|
|
|
|
|
столбцам |
|
|
|
|
Б |
символов |
|
|||||
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
к |
|
|
|
|
|
|
|
|
|
|
Рис. 7.11. Струк ура ТРС, сформированного из блоков кодов |
||||||||||||||||
|
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
||
Исходный массив инф рмационных бит последовательно, например, |
||||||||||||||||||
по строкам, записывается |
виде матрицы. Каждая строка матрицы представ- |
|||||||||||||||||
|
|
|
|
|
|
|
т |
|
|
|
|
|
|
|
и содержит k1 инфор- |
|||
ляет собой кодовое |
|
|
некоторого кода длиной n1 |
|||||||||||||||
|
|
|
|
|
слово |
|
|
|
|
|
|
|
|
|
|
|
||
мационных симво ов |
соответственно ( n1 k1 ) |
проверочных. Этот код по |
||||||||||||||||
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
||
аналогии с каскадным можно назвать внутренним кодом. Каждый столбец |
||||||||||||||||||
матрицы также представляет собой кодовое слово такого или другого блоко- |
||||||||||||||||||
|
|
|
л |
|
|
|
информационных и ( n2 k2 ) проверочных |
|||||||||||
вого кода дл ны n2 |
и содержит k2 |
|||||||||||||||||
|
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
символов. Это внешний код. |
|
|
|
|
|
|
|
|
|
|
|
|||||||
Скорость ТРС определяется как R R R k k |
2 |
/ n n . Расстояние Хем- |
||||||||||||||||
и |
|
|
|
|
|
|
|
|
1 |
2 |
1 |
|
1 |
2 |
|
|||
минга |
для |
ТРС |
равно |
произведению |
расстояния |
|
составляющих кодов: |
|||||||||||
dБd d |
. В качестве исходных блоковых кодов часто выбирают коды Хем- |
|||||||||||||||||
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
минга (расширенные или укороченные) или коды проверки на четность. |
||||||||||||||||||
Описанный метод кодирования обеспечивает независимость строк и столб- |
||||||||||||||||||
цов, поэтому введение более сложного перемежения не приводит к какому- |
||||||||||||||||||
либо заметному положительному результату. |
|
|
|
|
|
|
|
|||||||||||
115
Структурная схема кодера ТРС практически не отличается от схемы кодера каскадного типа: сначала информационные биты кодируются внешним кодом, а затем кодовые слова записываются в матричную память (например по строкам), считываются по строкам и кодируются внутренним кодом.
Структурная схема декодера ТРС также не отличается от декодера каскадного типа. Однако на первой итерации декодер внутреннего кода по каждому декодированному символу на основе критерия максимума апостериорной вероятности формирует мягкие решения для декодера внешнего кода. Но
второй итерации на вход декодера внутреннего кода подаются мягкие решения, достоверность которых уточнена после первой итерации и по строкам, и по столбцам. Окончательное решение о каждом переданном бите информации выносится после заданного числа итераций внешним декодером.
Основное отличие декодера турбокода от других декодеровРсостоит в том, что декодер турбокодов вычисляет мягкие решения для декодируемых
символов на всех итерациях их декодирования (кроме последнейИ), т.е. декодирование производится по принципу SISO. Асимптотически выигрыш от
кодирования с ростом отношения сигнал/шум при мягком декодировании |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
У |
|
может быть оценен по следующей формуле: |
|
Г |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
G 10 lg( R dmin ), . |
|
|
(7.15) |
||||
|
|
|
|
|
|
|
|
|
дБ |
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
|
|
|
|
|
к |
|
|
|
|
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
л |
|
|
|
|
|
|
|
|
|
|
|
б |
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
|
|
|
|
|
116

8.ПЕРЕМЕЖЕНИЕ ДАННЫХ
8.1.Общие сведения о перемежении данных
Перемежитель, или интерлевер (от англ. Interleaver, Interleaving) – фундаментальный компонент помехоустойчивого кодирования, предназначенный для борьбы с групповыми ошибками. Суть перемежения состоит в том, что производится изменение порядка следования символов информационной последовательности таким образом, что стоящие рядом символы оказываются разделенными несколькими другими. По сути дела, перемежение обеспечивает преобразование групповых ошибок в канале связи в одиночные.
Перемежители подразделяются на блоковые и свѐрточные. Блоковые устройства работают с двухмерными массивами информации, запись данных
в которых осуществляется по столбцам, а считывание – по строкам. На приѐ- |
|
ме запись и считывание осуществляются в обратном порядке. |
Р |
|
|
Перемежитель является одним из основных основным элементов тур- |
|
|
И |
бо-кодов, который меняет порядок символов входного сигнала или передает |
|
блок данных на вход следующего кодирующего устройства (рис. 8.1). Пере- |
|
|
У |
Г |
|
Б |
|
межение выполняется процессором в соответствии с алгоритмом перемеши- |
|
вания. Объединение перемеженных блоков данных с входными используется |
|
для снижения частоты ошибочных бит ав р ссм триваемом канале. Процесс перемежения увеличивает разнородность в д нных, поступающих в кодер, что приводит к исправлению ошибок в де одере (на приемной стороне) с помощью алгоритма исправления, сли символы искажаются при передаче.
Основная цель перемежит ля состоит в том, чтобы предложить каждо- |
|||||||||||||
|
|
|
|
|
|
|
|
|
к |
|
|
|
|
му кодеру некоррелированную или случайную версию информации, в ре- |
|||||||||||||
|
|
|
|
|
|
|
|
е |
|
|
|
||
зультате чего паритетные би ы каждого кодера становятся независимыми. |
|||||||||||||
|
|
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
|
о |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
и |
|
|
|
|
Кодер |
|
|
||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
л |
|
|
|
|
|
|
|
|
|
|
|
б |
|
|
|
|
|
|
|
|
||||
|
|
|
Переме- |
|
Кодер |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
||||
и |
|
|
|
|
жение |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||
Б |
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 8.1. Структурная схема устройства турбокодирования с перемежителем
Блок перемежения функционирует на основе матрицы, строки которой формируются последовательностью входных символов. Затем определенное число бит в зависимости от алгоритма перемежения образует блок. Из перемежителя данные передаются в блок кодера с помощью последовательного
117
вывода столбцов матрицы. В результате сигналы в расположенных рядом строках матрицы в потоке достоверных сигналов различаются номерами.
В соответствии с идеальной ситуацией количество столбцов и строк надо выбрать так, чтобы расстояние (разница в индексах символов входной последовательности) между соседними битами после перемежителя было наибольшим (для более эффективного исправления ошибок в декодере).
Из-за неконтролируемого увеличения числа строк образуется сигнальная задержка в схеме. В результате необходимо ограничивать размеры перемежителя с целью обеспечения задержки сигналов в допустимых пределах. С
другой стороны, уменьшение размеров матрицы ограничивает разделение |
|
|
Р |
сигналов на большое расстояние, а следовательно, снижает эффективность |
|
коррекции ошибок в декодере. |
И |
Существуют два основных метода перемежения: однородное (равно- |
|
мерное) и неоднородное (псевдонеравномерное). В случае однородного перемежения расстояние между двумя любыми соседними битами будет одинаковым. Это не является положительным качеством, поскольку результирующий выходной сигнал (на выходах обоих кодеров) характеризуется отно-
сительно невысоким минимальным расстоянием. |
|
У |
|
|
|
Неоднородное перемежение позволяет получить наилучшее «макси- |
||
|
Г |
|
Б |
|
|
мальное разбрасывание» данных и «максимальное упорядочивание» выход- |
||
а последовательности турбокодера. Минимкльное расстояние между символа-
ной последовательности информации. Это озн чает, что избыточность, вно-
симая двумя элементарными кодами, р вномерно распределена в выходной
однородного перемежения заключается в достижении достаточной неоднородности. К тому же условное перемежение требует существенного объема
ми в неоднородном перемеж нии при больших значениях блока увеличивается по сравнению с однородным п р м жением. Основная проблема для не-
памяти в кодере. Матрицы условного перемежения также требуют компенса-
ции задержек, которые |
граничивают их применение в соответствии с совре- |
|
менными требован |
|
т |
|
. |
|
|
о |
|
Помимо турбокодов перемежители является основным компонентом в |
||
кодах Рида–Со омона, в мобильных протоколах передачи данных (3GPP |
||
|
|
ями |
technical specification 36.212), в LDPC-кодах. Использование в системе пере- |
||
межителя повышаетлеѐ латентность, так как для обработки необходимо при- |
||
нять весь перемешанный блок данных. |
||
|
б |
|
и |
|
|
8.2. Кодирование информации в каналах связи на базе стандарта |
||
TETRA |
|
|
Б |
|
|
Рассмотрим, как обеспечивается применение перемежения информации для повышения помехоустойчивости передачи в реальных каналах связи. В каналах радиосвязи на базе стандарта TETRA для защиты от ошибок используется помехоустойчивое канальное кодирование сигнала, которое осуществ-
118

ляется путем введения в состав передаваемого сигнала достаточно большого объема избыточной информации (рис. 8.2).
|
|
|
|
|
|
|
|
|
|
Р |
|
|
|
|
|
|
|
|
|
И |
|
|
|
|
|
|
|
|
|
У |
|
|
|
|
|
|
|
|
|
Г |
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
|
|
|
к |
|
|
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
л |
|
|
|
|
|
|
|
|
|
|
б |
|
|
|
|
|
|
|
|
|
|
Р с. 8.2. Общая схема канального кодирования в стандарте TETRA |
||||||||||
иВ стандарте TETRA канальное кодирование реализуется в виде четы- |
||||||||||
рех процедур: |
|
|
|
|
|
|
|
|
|
|
БD – блочного кодирования; |
|
|
|
|
|
|
||||
E – сверточного кодирования; F – перемежения;
G – скремблирования.
При блочном кодировании входная информация разбивается на блоки по k символов, которые преобразуются по определенному закону в n-символьные блоки, где n k . Блочное кодирование предназначено в ос-
119
новном для обнаружения одиночных и групповых ошибок в канале связи и в определенных случаях для их исправления.
При сверточном кодировании каждый символ входной информационной последовательности, состоящий из k бит, преобразуется в n -битовый символ выходной последовательности, причем n k . Сверточное кодирование является мощным средством борьбы с одиночными ошибками, хотя и не обеспечивает их обнаружения.
При перемежении производится изменение порядка следования символов информационной последовательности таким образом, что стоящие рядом
символы оказываются разделенными несколькими другими. Перемежение |
|
|
Р |
обеспечивает преобразование групповых ошибок в канале связи в одиноч- |
|
ные. |
И |
|
Скремблирование состоит в преобразовании входной информационной |
последовательности в выходную путем ее побитного сложения по модулю 2 со специально формируемой шифровальной последовательностью. Скремблирование используется для определенной защиты передаваемой информации, а также для аутентификации абонентов.
Стандарт TETRA описывает процесс канального кодирования как по- |
|
|
У |
следовательное преобразование данных на четырех уровнях, при этом вход- |
|
Г |
|
Б |
|
ные данные обозначаются как биты типа 1 в блоках типа 1, данные после |
|
блочного кодирования – биты типа 2 в блок х типа 2 и т. д. После блочного кодирования к битам, закодированным блочным кодом, добавляются так
называемые «хвостовые» биты. |
|
|
а |
|
|
|
|
бит входной по- |
|
При перемежении обесп чива тся преобразование K3 |
||||
следовательности, полученной в р кзультате сверточного кодирования, в K 4 |
||||
бит выходной последовательности, причем K3 K 4 , т. е. |
перемежение не |
|||
|
е |
|
|
|
Таким образ м, в системах |
связи, работающих на базе данного стан- |
|||
вносит в сигнал избыточнос ь, а |
олько производит перестановку бит в ин- |
|||
формационном блоке. |
|
|
|
|
дарта, перемежен е осп льзуется для преобразования групповых ошибок, возникающих в канале связи из-за наличия глубоких замираний сигнала в
условиях много учевого распространения, в одиночные, с которыми легче |
|||
|
|
|
и |
бороться с помощью блочного и сверточного кодирования. |
|||
В стандартелTETRA применяется 2 вида перемежения: блочное и пере- |
|||
межен е по |
N |
локам. |
|
|
б |
||
и |
|
|
|
8.3. |
Блочное перемежение |
||
Б |
|
|
|
Обозначим блочный перемежитель как K , J , где K означает количе-
ство бит во входном информационном блоке, а J – количество бит, на которое разносятся соседние для входного блока биты. При блочном перемежении соответствие бит выходного блока битам входной последовательности, т. е. b4( k ) b3( i ), где i 1,2,...,K 1, производится по следующему правилу:
120
k 1 (J i)modK . |
(8.1) |
Работу схемы блочного перемежителя можно представить как проведение последовательной построчной записи входной информационной последовательности в матрицу, в которой длина строки соответствует J (число столбцов ( K div J 1) ), а затем считывание записанной информации по
столбцам. Оператор div J означает результат целочисленного деления.
пользуется в каналах SCH/HD, SCH/HU, SCH/F, BNCH, STCH, BSCH и
TCH/S.
Блочное перемежение с различными параметрами преобразования ис- Р
8.4.Перемежение по N блокам
|
|
|
И |
|
|
У |
|
Перемежение по |
Г |
|
|
N блокам применяется в логических каналах переда- |
|||
|
Б |
|
|
чи данных типа TCH/2,4 и TCH/4,8, информация по которым передается блоками, длиной 432 бита.
При данной схеме перемежения блочная перестановка бит дополняется так называемым диагональным перемежением. Его особенностью является то, что оно производится одновременно для нескольких последовательных
блоков, т. е. может осуществляться перест новка битов из одного блока в |
|||||||
другой. Количество блоков N , участвующихав перемежении, может быть |
|||||||
равным 1, 4 или 8 ( N 1 |
– вырожд нный случай, при котором перемежение |
||||||
|
|
|
|
|
к |
|
|
осуществляется в пределах одного блока). При этом в результате перемеже- |
|||||||
ния образуется M N 1 блоковепо 432 бита, где M – целое число, т. е. про- |
|||||||
цедура перемежения |
N бл кам может увеличивать общее количество ин- |
||||||
формационных блок в. |
|
|
т |
|
|
|
|
Таким образом, |
|
|
|
|
|
||
|
|
перемежении по N блокам преобразование вход- |
|||||
ной информации про позвод тся в 2 этапа: 1-й этап – диагональное перемеже- |
|||||||
|
при |
|
|
|
|
||
ние с увеличением общего количества блоков, 2-й этап – блочное перемеже- |
|||||||
M N 1блокB3'(1), B3'(2),..,B3'( M N 1). Если обозначить k -й бит бло- |
|||||||
ние в каждом из по ученных блоков. |
|
|
|||||
и |
|
|
|
|
|
|
|
ПервоначальнолM |
блоков B3(1), B3(2),.., B3(M), участвующих в преоб- |
||||||
разован , с помощью |
|
диагонального перемежителя преобразуются в |
|||||
Б |
|
|
k 1,2,...,432 , а m 1,2,...,M N 1, то |
|
|||
ка B3'(m) как b3'(m,k), где |
|
||||||
|
|
|
|
|
|
при 1 m j M , |
(8.2) |
|
b3 ( m,k ) b3( m j, j 1 ( i N )) |
||||||
|
|
|
|
|
1 m j |
и m j M , |
(8.3) |
|
b3 ( m,k ) 0 при |
||||||
при этом j и k определяются следующими выражениями:
121
j ( k 1) div ( 432 / N ), |
(8.4) |
|
|
i (k 1) mod (432 / N). |
(8.5) |
Практически это означает формирование M N 1 блоков, каждый из которых состоит из 1/ M частей следующих друг за другом M блоков (при M = 2 это половина блока, при M = 3 – 1/3 блока и т. д.). Для первых
и последних блоков, количество которых соответствует увеличению общего числа блоков, свободные разряды заполняются нулями. При M = 2 нулями заполняется вторая половина первого и первая половина последнего блока, при M = 3 нулями заполняются первые две трети первого блока, первая треть второго блока, первая треть предпоследнего блока и первые две трети последнего блока. При этом следует учитывать, что предварительно в каждом
из блоков биты также переставляются путем сборки в блоке сначалаРбит с |
||||||||||||
номерами 1,1+M,1+2M,…, затем 2,2+M,2+2M,… и т. д. |
|
|
||||||||||
На втором этапе производится блочное перемежение Ибит в каждом из |
||||||||||||
полученных блоков в соответствии с правилом |
У |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(8.6) |
|
|
|
|
|
|
b4(m,i) b3 (m, k),Г |
||||||
|
|
|
|
|
|
|
|
|
|
Б |
|
(8.7) |
|
|
|
|
|
где i 1 (103k) mod 432 , |
|
||||||
|
|
|
|
|
|
k 1, 2,...,432 . |
|
|
|
(8.8) |
||
|
|
|
|
|
|
|
|
а |
|
|
||
|
|
|
|
|
|
|
к |
|
|
|
|
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
л |
|
|
|
|
|
|
|
|
|
|
|
б |
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
|
|
|
|
|
122
9.ФОРМИРОВАНИЕ ЦИФРОВЫХ ПОТОКОВ
9.1.Вводные замечания
Цифровые потоки – это последовательности 0 и 1, передаваемые по линии связи. Нули и единицы могут нести информацию о речи, тексте, изображении и т.д. При этом скорости потоков будут, естественно, отличаться: для текста – 50...100 бит/с, для компьютерных данных – 200 бит/с и выше, для речи – 64 кбит/с, для подвижной «картинки» – более 100 Мбит/с.
Как же «строить» цифровые системы передачи? Сколько цифровых потоков можно объединять и направлять в одну линию связи – провод в электрическом кабеле, ствол в радиорелейной или спутниковой линиях, волоконный световод в оптическом кабеле? Можно ли стандартизировать скорости
передачи? |
Р |
|
|
Начнем с того, что узлы различных систем передачи должны быть од- |
|
нотипными, или унифицированными. |
И |
|
|
Цифровые системы передачи создают во всем мире; коммуникации |
|
связи не знают государственных границ. Каждая страна должна выпускать |
|
|
У |
Г |
|
Б |
|
аппаратуру, согласовывая ее со стандартами, принятыми в других странах. Государства должны договориться, на каких принципах строить аппаратуру. С этой целью создан межгосударственный орг н – Международный союз
|
к |
электросвязи (МСЭ). Он рекомендует строить цифровые системы передачи |
|
по иерархическому принципу. |
е |
Примером иерархического построания системы является календарь. |
|
Иерархия календаря состоит в сл дующ м. За единицу измерения выбраны сутки. Семь суток объединяются в н д лю. Из четырех или четырех с половиной недель образуется месяц. Три месяца составляют квартал. Четыре квартала – это год. Г ды складываю ся в десятилетия и века, а века – в тыся-
хожа на иерархиюлдимока ендаря. Прежде всего необходимо было выбрать некоторую единицу измерения – «элементарную» скорость цифрового потока, единую для всех стран и предприятий, выпускающих аппаратуру систем пе-
челетия. При необх |
сти |
иерархию можно продолжить и «вниз» от |
суток: сутки состоят |
эту |
|
з 24 час в, час – из 60 мин и т.д. |
||
Иерархия, рекомендованнаяо |
для цифровых систем передачи, чем-то по- |
|
редачи, позволяющую измерять скорость суммарных цифровых потоков. |
||
|
|
б |
Такая «ед н чная» скорость во всем мире – скорость передачи оцифрован- |
||
ной |
|
, равная 64 кбит/с. Выбор этой величины в качестве единицы объ- |
|
речи |
|
единения цифровых потоков связан, скорее, с традициями, нежели с какими- |
||
то другими соображениями. |
||
Б |
|
|
|
Канал, в котором информация передаются со скоростью 64 000 бит/с, |
|
получил название основного цифрового канала (ОЦК). Возможности любой цифровой системы передачи оцениваются числом организованных с ее помощью именно таких стандартных каналов.
123

9.2.Цифровые иерархии
9.2.1. Плезиохронная цифровая иерархия
Исторически появившаяся первой плезиохронная цифровая иерархия (ПЦИ) имеет европейскую, североамериканскую и японскую разновидности
(табл. 9.1).
Для цифровых потоков ПЦИ применяют соответствующие обозначе- |
||||||||||||||||
ния. Для североамериканской и японской ПЦИ применяется обозначение T |
||||||||||||||||
(иногда DS), для европейской ПЦИ – Е. Цифровые потоки первого уровня |
||||||||||||||||
обозначаются соответственно Т-1 и E-1, второго Т-2 и Е-2 и т.д. |
Р |
|||||||||||||||
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
И |
||||
|
|
|
|
|
|
|
|
|
|
|
У |
|
|
Таблица 9.1 |
||
|
|
|
|
Иерархия цифровых потоков |
|
|
|
|
|
|||||||
Уровень |
Европа |
|
Северная Америка |
|
|
Япония |
||||||||||
иерархии |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
|
Скорость, |
|
Коэф. |
|
Скорость, |
|
Коэф. |
Скорость, |
Коэф. |
|||||||
|
Мбит/с |
|
мульти- |
|
Мбит/с |
|
мульти- |
|
|
|
|
|
мульти- |
|||
|
|
|
|
плекс. |
|
|
|
|
|
плекс. |
|
|
|
|
|
плекс. |
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
|
||
0 |
0,064 |
|
|
- |
|
0,064 |
|
|
- |
|
0,064 |
|
|
- |
||
1 |
2,048 |
|
|
30 |
|
1,544 |
|
|
24 |
|
1,544 |
|
|
24 |
||
2 |
8,448 |
|
|
4 |
|
6,312 |
|
|
4 |
|
6,312 |
|
|
4 |
||
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
|
|
|
3 |
34,368 |
|
|
4 |
|
44,736 |
|
|
7 |
|
32,064 |
|
|
5 |
||
|
|
|
|
|
|
к |
|
|
|
|
|
|
|
|
||
4 |
139,264 |
|
|
4 |
|
- |
|
|
- |
|
97,728 |
|
|
3 |
||
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
|
|
Чем выше ступень иерархии, тем мощнее цифровой поток, т. е. тем |
||||||||||||||||
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
||
выше его скорость. К сис емам передачи, |
стоящим в самом низу иерархиче- |
|||||||||||||||
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ской лестницы, отн сится цифровой поток E1 (30 стандартных |
|
основных |
||||||||||||||
цифровых каналов). У п д бных систем передачи скорость цифрового потока относите льно невысока (около 2 Мбит/с для E1), что ограничивает сферу их примененияб.
и9.2.2. Структура цифрового потока Е1
БЦифровой поток преобразуется в блоки стандартной логической структуры – циклы. Цикловая структура обеспечивает работу процедур мультиплексирования и демультиплексирования («вставки» и «вырезки» конкретного основного цифрового канала), передачу управляющей информации, а также встроенную диагностику по параметру ошибок в цифровой системе передачи. Существует три основных варианта цикловой структуры Е1: неструктурированный поток, поток с цикловой структурой и с цикловой и сверхцикловой структурой.
124
Неструктурированный поток Е1 используется в сетях передачи данных
ине имеет цикловой структуры, т. е. разделения на каналы (основные цифровые каналы).
Поток Е1 с цикловой структурой предусматривает разделение на 32 канала ОЦК по 64 кбит/с в форме разделения на канальные интервалы (Time Slot – TS) от 0 до 31. Цикловая структура приведена на рис. 9.1. Для каждого канального интервала в составе цикла отводится 8 бит, таким образом длина цикла равна 256 бит, что при заданной скорости передачи Е1 составляет 125 мкс (длительность одного цикла). Тридцать канальных интервалов (1–15
и17–31) используются для передачи информации (например голоса). Нулевой канальный интервал отводится под передачу сигнала цикловойРсинхронизации FAS (Frame Alignment Signal), шестнадцатый – для передачи служебной информации. И
Структура FAS представлена на рис. 9.2. Различаются четные и нечетные циклы. В TS0 нечетных циклов передается сигналУFAS (на рисунке – первая строчка), который включает в себя последовательность цикловой синхронизации 0011011 и один служебный бит, зарезервированныйГ под задачи международного использования. В TS0 четныхБциклов передается сигнал NFAS, не содержащий кодовой последовательность цикловой синхронизации.
Всоставе сигнала NFAS передаетсяабит Si, зарезервированный под задачи международного использованияк, бит А, используемый для передачи сигналов о неисправностях, а также пять служебных бит Sn4, Sn5, Sn6, Sn7, Sn8, используемые для передачиесигналов сетевого управления первичной сети Е1, диагностики и дополнит льных процедур контроля ошибок.
Вотечественной терминологиит вариант потока Е1 с цикловой структурой получил название ИКМ-31. Он используется в ряде систем передачи данных, а также в нек от рых приложения ОКС7, ISDN и B-ISDN.
Сверхцикловаяиструктура потока Е1. В этом случае поток Е1 имеет дополнительно к ц кл в й структуре еще и сверхцикловую структуру (MFAS – MultiлFrame Alignment Signal). В отечественной терминологии такой вариант цикбовой структуры Е1 получил название ИКМ-30. При этом 16 циклов о ъединяются в сверхцикл размером 4096 бит и длительностью 2 мс. Когдаидетпередача/прием информации в виде сверхциклов MFAS, индивидуальная нформация FAS каждого цикла теряет значимость. Необходимо рассматрБ вать всю информацию FAS – 16 циклов.
Первый цикл содержит информацию MFAS о сверхцикле в шестнадцатом канальном интервале, а остальные 15 интервалов используются для передачи сигнальной информации. Структура MFAS показана на рис. 9.3.
Процедуры контроля ошибок передачи. Использование избыточного кода CRC-4. Передача потока Е1 с цикловой структурой ИКМ-30 имеет важный механизм – процедуру встроенной диагностики параметров
125
|
|
|
|
|
|
|
|
|
|
|
|
Р |
|
|
|
|
|
|
|
|
|
|
|
И |
|
|
|
|
|
|
|
|
|
|
|
У |
|
|
|
|
|
|
|
|
|
|
|
Г |
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
|
|
|
|
|
к |
|
|
|
|
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
л |
|
|
|
|
|
|
|
|
|
|
|
б |
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
|
|
|
|
|
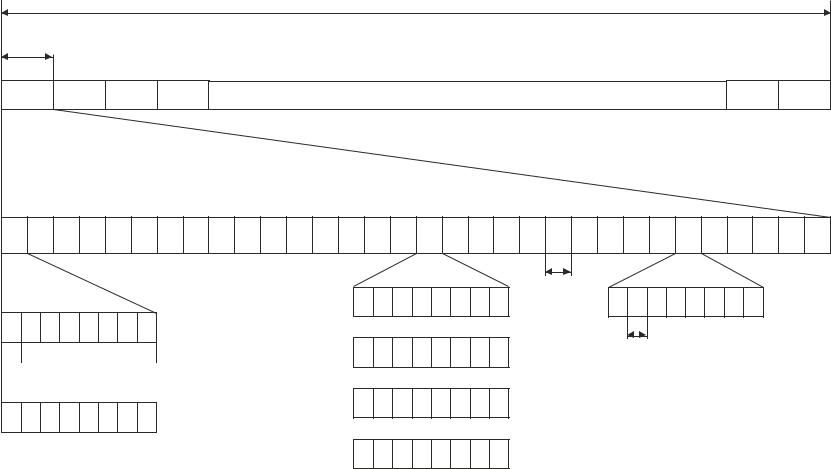
126 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Сверхцикл 2мс |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
125 мкс |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Ц0 |
|
|
Ц1 |
|
Ц2 |
|
|
Ц3 Циклы ИКМ-30 группируются в сверхциклы Ц0-Ц15 для распределения сигналов СУВ |
|
Ц14 |
Ц15 |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Р |
|
|
|
|
||
Каждый цикл разбит на 32 канальных интервала КИ0-КИ31 по |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
|
|
|
|
|
|
|||||||||||||||||||
восемь тактовых интерваловразрядов Р1-Р8. В течение КИ длительностью 3,91 мкс |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
передаѐтся кодовая комбинация одного телефонного канала, состоящая из последовательности |
|
|
У |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
символов 0 и 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
КИ КИ КИ КИ КИ КИ КИ КИ КИ КИ КИ КИ КИ КИ КИ КИ КИ КИ КИ КИ КИ КИ КИ КИ КИ КИ КИ КИ КИ КИ КИ КИ |
|||||||||||||||||||||||||||||||||||||||||
0 |
1 |
|
2 |
3 |
4 |
|
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
|
15 |
16 |
17 |
|
18 |
19 |
|
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
31 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Г |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3,91 мкс |
|
Кодовая комбинация |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
|
0 |
0 |
1 |
Y |
0 |
1 |
Б |
P1 P2 P3 P4 P5 P6 P7 P8 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Цикл Ц0 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
КИ0 в четном цикле |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
ДИ 0 |
|
0 |
1 |
1 |
0 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Цикл Ц1 |
|
СК СК |
0 |
|
|
|
|
|
|
|
|
488 нс |
|
|
|
|
|
|
|
|||||||||
Цикловой синхросигнал |
|
|
|
|
|
|
1 СК СК |
0 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
16 |
16 |
|
|
|
|
Начало сверхцикла определяется по цикловому синхросигналу |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
к |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вида 0000. Разряд Р6 КИ16 ВЦ0 используется для передачи |
||||||||||||
КИ0 в нечетном цикле |
|
|
|
|
|
|
Цикл Ц2 |
|
СК СК |
0 |
1 |
СК СК |
0 |
1 |
|
|
аварийного сигнала в сбое сверхциклового синхронизма “Y”. |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
е |
|
|
|
|
|
В циклах Ц5-Ц15 в КИ16 передаются сигналы управления |
|||||||||||||||||
ДИ 1 |
|
X |
|
|
A |
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
17 |
17 |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. . . . . . . . |
|
|
и взаимодействия (СУВ) между АТС. |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
СК СК |
0 |
1 СК СК 0 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Ц кл Ц15 |
15т15 |
30 30 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Начало цикла определяется по цикловому синхрос гналу |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
вида 0011011, передаваемому в разрядах Р2-Р8 КИ0 ЧЦ. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Первый разряд КИ0 отводится для передачи дискретной информации, разряд КИ3 НЦ – для передачи сигналов аварии о |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
потери цикловой синхронизации “X”. |
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Прием значения 0 соответствует норма ьному состоянию, а 1 – аварийному. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
В тактовом интервале Р2 постоянно передаѐтся 1 (в отличие от Р2 в цикловом синхросигнале), что необходимо для |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
л |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
проверки в процессе поиска ЦСС. Остальные разряды могут быть использованы для служебной информации. |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
Так, в первых модификациях АЦО шестой разряд используется для передачи сигнала контроля остаточного затухания A |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
Рис. 9.1 Структура потока E1 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
Р |
|
|
|
|
|
|
|
|
|
|
|
И |
|
|
|
|
|
|
|
|
|
|
|
У |
|
|
|
|
|
|
|
|
|
|
|
Г |
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
|
|
|
|
|
к |
|
|
|
|
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
л |
|
|
|
|
|
|
|
|
|
|
|
б |
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
|
|
|
|
|
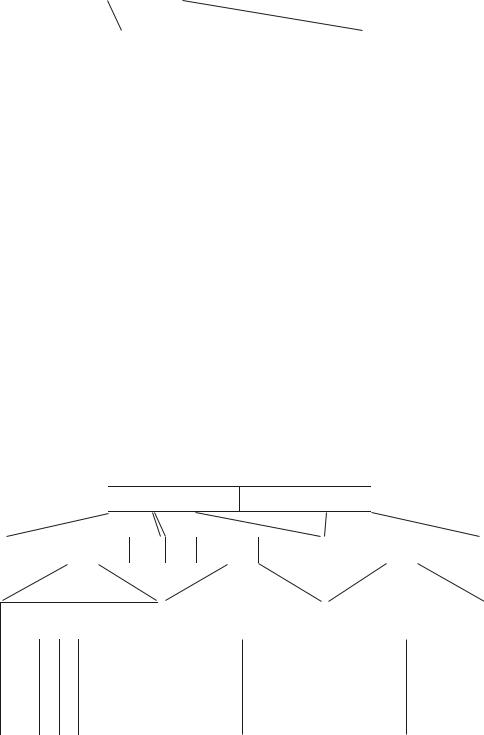
|
|
|
|
Time slot 0 |
1 |
... |
31 |
|
|
|
|
|
|
|
BITS |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
|
|
|
|
|
|
Si |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
|
|
|
|
|
|
|
|
Si |
1 |
A |
Sn |
Sn |
Sn |
Sn |
Sn |
|
|
|
|
|
|
|
|
Рис. 9.2. Структура нулевого канального интервала потока E1
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Первая строка содержит сигнал FAS. |
|
|
Р |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Вторая строка содержит сигнал NFAS. |
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
Sn = биты, зарезервированные под задачи национального исполь- |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
зования. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
Si = биты, зарезервированные под задачи международного исполь- |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
зования. |
|
|
|
|
|
|
|
|
|
У |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Последовательность FAS = 0011011. |
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Г |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
|
|
|
|
||||||
ошибки. Для этой цели используется биты Si в составе циклового заголовка |
|||||||||||||||||||||||||||||||||||||||||||||||
FAS и NFAS. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
метра |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Процедура использует сверхцикловую структуру в 16 циклов, как пока- |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
к |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
зано на рис. 9.3, и механизм расчета п р |
|
|
ошибки по контрольному из- |
||||||||||||||||||||||||||||||||||||||||||||
быточному коду CRC-4 (полином X(4) +X + 1). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
Цикл 0 |
|
|
|
т |
|
2 |
|
Цикл 3 |
... |
|
|
Цикл |
15 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Цикл 1 |
|
Цикл |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
TS 0 |
... |
|
TS 16 |
... |
|
TS 31 |
|
|
|
TS 0 |
... |
|
TS 16 ... |
TS 31 |
|
|
TS 0 |
... |
|
TS 16 |
... |
TS 31 |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
л |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Биты |
|
|
|
|
|
|
|
|
|
|
|
|
Биты |
|
|
|
|
|
|||||||||
|
|
|
|
|
Б ты |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
3 |
4 |
5 |
6 |
|
7 |
8 |
|
|
1 |
2 |
|
3 |
4 |
|
5 |
6 |
7 |
8 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A B C D A B C D |
|
A B C D A B C D |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
Б |
0 |
0 |
0 |
0 |
|
X |
Y |
X |
|
X |
|
|
|
|
Канал 1 |
|
|
|
|
Канал 16 |
|
|
|
|
Канал 15 |
|
|
|
Канал 30 |
|
|
|
|||||||||||||||
|
|
|
|
|
|
(TS-1) |
|
|
|
|
(TS-17) |
|
|
|
|
(TS-15) |
|
|
|
|
(TS-31) |
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 9.3. Структура сверхцикла Е1
Сигнал MFAS = 0000XYXX
X – запасные биты (1 обычно не используется);
Y – удаленная неисправность MFAS ( равно 1 в случае, если потеряна сверхцикловая синхронизация).
Принцип CRC-4 базируется на простом математическом расчете, производимом в каждом сверхцикле данных. Оборудование передачи Е1 произ-
127
водит расчет суммы CRC-4 и включает результаты суммы в сигнал следующего сверхцикла. Оборудование приемника принимает сигнал и производит аналогичный расчет и сравнение полученной суммы и переданной в следующем сверхцикле. Если в двух полученных суммах имеется расхождение, генерируется сигнал ошибки CRC-4. В настоящее время в оборудование и системы самодиагностики цифровых каналов ИКМ встраивается функция анализа по CRC-4. Часто возникает вопрос о целесообразности проведения анализа по BER, если система и так анализирует параметр ошибки по CRC-4.
Отвечая на этот вопрос, необходимо учесть два основных принципа |
|
использования CRC-4. Во-первых, каждая ошибка CRC-4 необязательно свя- |
|
|
Р |
зана с ошибкой одного бита информации. Несколько битовых ошибок в од- |
|
ном сверхцикле дадут только одну ошибку CRC-4 для блока. Во-вторых, не- |
|
И |
|
сколько битовых ошибок могут компенсировать друг друга в смысле значе- |
|
ния суммы CRC-4. CRC-4 является удобным методом контроля ошибок в |
|
У |
|
процессе сервисного мониторинга при работающем канале, когда практиче- |
|
ски невозможно измерить реальные параметры ошибок по битам, поскольку
менее, в режиме с отключением канала необходимоГпроводить измерения ошибок по битам, поскольку результаты таких измерений более точны.
невозможно добиться синхронизации тестовой последовательности. Тем не
этой информации используется сверхциклов Бя структура. Однако сверхцикл CRC-4 необязательно связан со сверхциклом MFAS. Каждый сверхцикл мо-
Рассмотрим механизм передачи информации о CRC-4. Для передачи
а жет быть разбит на 2 подцикла (SMF)к. В т бл. 9.2 ниже они отмечены как
SMF#1 и SMF#2 и содержат пое8 ци лов аждый. Соответственно отмечены по 4 бита, используемые для п р дачи CRC-4 каждого сверхцикла (биты С). Биты CRC-4 вычисляются м тодом д л ния двоичной суммы содержания 8 последовательных циклов на ес овый полином, остаток от деления в виде 4-
битового сообщения вс авляе ся в следующий сверхцикл для передачи в по-
токе Е1. |
|
т |
|
|
|
Структура сверхцикла CRC-4 включает несколько сообщений |
||
|
о |
|
|
и |
|
сверхцикловой структуры CRC-4. В четных циклах MFAS битами Si переда-
ется |
сообщение |
сверхцикловой синхронизации CRC-4 – комбинация 001011, |
|
||
которая испо ьзуется на приемной стороне для синхронизации по CRC. Кро- |
||
и |
|
|
ме этого, в лсоставе сверхцикла SMF передается его главная информация – |
||
сообщен е C1C2C3C4. В качестве дополнительного сообщения, передавае- |
||
Б |
|
|
мого в направлении передачи при обнаружении ошибки по CRC-4, используется 2-битовое сообщение Е1Е2. Каждый бит Е связан с одним из принятых сверхциклов SMF (в составе сверхцикла MFAS используется два сверхцикла SMF, поэтому сообщение использует два бита Е). Когда оборудование приемника получает информацию об ошибке CRC-4, оно генерирует бит Е для сообщения передатчику о принятой ошибке.
Мониторинг по CRC производится в режиме реального времени непосредственно после установления циклового синхронизма. В этом случае возникает цикловая синхронизация по CRC-4 и сверхциклам SMF по кодовой последовательности 001011. Эта синхронизация достаточно устойчивая, по-
128

теря цикловой синхронизации по CRC-4 отображается только после того, как более чем 914 сообщений CRC в секунду не соответствует ожидаемым значениям.
|
|
|
|
|
|
|
|
|
|
|
|
|
Канальный интервал 0 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Биты |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Сверхцикл |
Подцикл |
Цикл |
|
|
Бит 1 |
|
Бит 2 |
Бит 3 |
Бит 4 |
Бит 5 Бит 6 |
Бит 7 |
Бит 8 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
FAS |
|
1 |
|
|
С1 |
|
0 |
|
0 |
1 |
1 |
|
|
0 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
NFAS |
|
2 |
|
|
0 |
|
1 |
|
А |
Sn4 |
Sn5 |
|
|
Sn6 |
Sn7 |
Sn8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
С1 |
|
0 |
|
0 |
1 |
1 |
|
|
0 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
SMF#1 |
|
4 |
|
|
0 |
|
1 |
|
А |
Sn4 |
Sn5 |
|
|
Sn6 |
Sn7 |
Sn8 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
5 |
|
|
С3 |
|
0 |
|
0 |
1 |
1 |
|
|
0 |
1 |
1 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
Sn7РSn8 |
|
||
|
|
|
|
|
|
6 |
|
|
0 |
|
1 |
|
А |
Sn4 |
Sn5 |
|
|
Sn6 |
|
||
|
|
|
|
|
|
7 |
|
|
С4 |
|
0 |
|
0 |
1 |
1 |
|
|
0 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
|
|
|
|
|
|
|
|
|
8 |
|
|
0 |
|
1 |
|
А |
Sn4 |
Sn5 |
|
|
Sn6 Sn7 |
Sn8 |
|
|
|
|
|
|
|
|
9 |
|
|
С1 |
|
0 |
|
0 |
1 |
1 |
|
|
0 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
1 |
|
1 |
|
А |
Sn4 |
Sn5 |
|
|
Sn6 |
Sn7 |
Sn8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Г |
|
|
|
|
|
|
|
|
|
|
|
|
11 |
|
|
С2 |
|
0 |
|
0 |
1 |
1 |
|
0 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
|
|
|
|
SMF#2 |
|
12 |
|
|
1 |
|
1 |
|
А |
Sn4 |
Sn5 |
|
|
Sn6 |
Sn7 |
Sn8 |
|
||
|
|
|
|
|
|
13 |
|
|
С3 |
|
0 |
к |
Б1 1 |
|
|
0 |
1 |
1 |
|
||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
||||||||
|
|
|
|
|
|
14 |
|
|
E1 |
|
1 |
|
А |
Sn4 |
Sn5 |
|
|
Sn6 |
Sn7 |
Sn8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
15 |
|
|
С4 |
|
0 |
|
0 |
1 |
1 |
|
|
0 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
16 |
|
|
E2 |
|
1 |
|
А |
Sn4 |
Sn5 |
|
|
Sn6 |
Sn7 |
Sn8 |
|
|
|
|
|
|
|
Рис |
|
. 9.4. |
|
Серуктура подциклов SMF: |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
и |
|
SMF#1 – подцикл 1; |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
тSMF#2 – подцикл 2; |
|
|
|
|
|
|
|
|||||||||
|
|
|
л |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
с1, с2, с3, с4 – биты CRC; |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
001011 – с гнал сверхцикловой синхронизации CRC; |
|
|
|
|||||||||||||||
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Биты E1 и Е2 идентифицируют ошибку по CRC (E=1 – нет ошибки, |
|
|
||||||||||||||||||
и |
|
|
|
|
|
|
Е=0 – ошибка по CRC). |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Sn = ты, зарезервированные под задачи национального использования |
|
|
|||||||||||||||||||
Б |
|
|
для передачи управляющей информации сетевого уровня |
|
|
|
|||||||||||||||
|
|
|
|
|
|
||||||||||||||||
Сетевой уровень потока Е1. Стандартизация систем передачи Е1 охватывает также третий, сетевой уровень, где осуществляются процедуры управления первичной сетью. При работе процедур управления они широко используют сигналы о неисправностях, генерируемые в современных цифровых системах передачи, а также сигналы о возникновении ошибок, фиксируемые встроенными средствами диагностики. Эта информация собирается в узлах системы управления и обрабатывается. Таким образом, сетевой уровень Е1 включает в себя набор определенных служебных сигналов и сообще-
129
ний, используемых системой управления первичной сетью. Такие сообщения делятся на три категории:
–сообщения о возникновении ошибок в системе передачи;
–сообщения о неисправностях, возникающих в системе передачи;
– сообщения, используемые для реконфигурации первичной сети и восстановления плана синхронизации.
Последняя категория сообщений сетевого уровня Е1, получивших название сообщений SSM (System Synchronization Messages – сообщения в системах синхронизации), будет отдельно рассматриваться в главе, посвя-
щенной проблемам построения и эксплуатации современных систем синхро- |
|
|
Р |
низации. Здесь же мы рассмотрим первые две категории сообщений. |
|
Сообщение о возникновении ошибок в системе передачи Е1 использует |
|
И |
|
сообщения E1E2. Действительно, сообщения, передаваемые битами Е, слу- |
|
жат подтверждением возникновения блоковой ошибки CRC и могут служить |
|
У |
|
критерием качества цифровой системы передачи. Система управления анали- |
|
зирует значения бит Е и собирает информацию о возникающих в системе пе- |
|
редачи Е1 ошибках. |
Г |
|
Б |
Сообщения о неисправностях в системе передачи передаются циклами |
|
NFAS, а также битами MFAS в случае, если поток Е1 имеет сверхцикловую |
|
структуру. Как было описано в предыдущем подразделе, в состав четных циклов NFAS входят биты, зарезервиров нные под задачи национального использования – бит А и биты Sn4, Sn5, Sn6, Sn7, Sn8. Именно эти биты ис-
пользуются для передачи различных сообщений о неисправностях в цифро- |
|||
|
|
|
а |
вой систем передачи. Биты Sn образуют своего рода канал управления, ре- |
|||
сурсы которого используются с вымкуровнем Е1. Помимо битов Sn для пе- |
|||
редачи сообщений о неисправностях могут использоваться биты XXYX |
|||
MFAS. |
|
е |
|
|
|
|
|
Эти биты исп льзую ся главным образом для передачи сигналов о не- |
|||
исправностях в |
в й структуре Е1 (так, бит Y непосредственно и |
||
определяется как |
т |
|
|
нд кат р неисправности MFAS на удаленном конце). Бит |
|||
|
о |
|
|
А (иногда он называется также Sn3) представляет собой бит оперативного |
|||
сигнала о неисправности. В случае возникновения существенной неисправ- |
|
|
сверхцикл |
ности, тре ующей оперативного вмешательства, бит А становится равным |
|
единице. Такуюлсущественную неисправность называют RDI (Remote Defect |
|
Indication – ндикация дефекта на удаленном конце). |
|
б |
|
В случае возникновения так называемого «неоперативного» сигнала |
|
Бнеисправностии , система передачи генерирует NFAS с инверсией бита Sn4 с 0 на 1. Рекомендации ITU-T устанавливают следующие возможные причины генерации такого сигнала:
–в случае, если параметр ошибки BER в FAS становится хуже, чем
10(–3);
–в случае неисправности в цепи питания кодека;
–в случае, если потерян входной сигнал или имеет место сбой цикловой синхронизации.
130
Неоперативный сигнал о неисправности дает возможность получения информации о значительном увеличении параметра ошибки на стороне передатчика. Оборудование приемника обычно имеет установленные пороговые значения для генерации сигнала Sn4. В случае увеличения параметра ошибки более порога приемник генерирует сигнал «неоперативной» неисправности в направлении передатчика. При получении этого сигнала система управления может перевести передачу на резервный канал Е1, за счет чего достигается высокое качество связи.
Биты Sn5, Sn6, Sn7, Sn8 образуют служебный канал передачи данных
емкостью 2 кбит/с, который может использоваться для передачи сигналов о
важно не абсолютное значение бит Sn, а последовательность сигналовР, генерируемых в этих битах. Каждый бит образует так называемый «вертикаль-
неисправностях. В последнее время в связи с развитием систем управления (в частности платформы TMN) возможности этого канала используются до-
вольно широко. Речь здесь идет именно о канале, поскольку в этом случае
ный протокол», т. е. сообщение о неисправности передается не одним, а не- |
|||
сколькими последовательными битами Sn. |
|
|
И |
|
|
|
|
Тип передаваемых сообщений и алгоритм их генерации устанавливает- |
|||
|
|
У |
|
ся национальными стандартами, производителями оборудования или специ- |
|||
|
Г |
|
|
|
Б |
|
|
альными требованиями (например операторов ведомственных сетей). |
|||
а маемые оборудованием сообщения могуткуспешно использоваться системами
Наибольшее распространение получил ст нд рт ETS 300-233, определяющий
использование бит Sn в мультиплексор х PRI ISDN. Генерируемые и прини-
управления, которые работают на принципах анализа именно этих сообщений. Таким образом, сообщения о н исправностях представляют собой базу
для создаваемых систем управл ния, их количество непосредственно опреде- |
|||||
|
|
|
|
е |
|
ляет максимальный уровень ин еллектуальности системы управления и пе- |
|||||
речень параметров, д ступных для контроля сети. |
|||||
Использование бит в Sn |
|
возможность разграничить степень ответ- |
|||
|
|
|
дает |
|
|
ственности разл чных перат ров. В качестве иллюстрации рассмотрим не- |
|||||
|
|
|
о |
|
|
сколько примеров (р с. 9.2), где представлены два варианта использования |
|||||
битов Sn, позво яющихопределить сторону, ответственную за ухудшение |
|||||
качества передачи. |
|
|
|
||
|
|
л |
|
|
|
|
б |
|
|
|
|
9.2.3. Мультиплексирование цифровых потоков |
|||||
и |
|
|
|
|
|
Б |
|
|
|
|
|
К системам передачи, стоящим в самом низу иерархической лестницы, относится аппаратура ИКМ-30 (30 – число организуемых основных цифровых каналов), использующая цифровой поток первого уровня Е1). У подобных систем передачи сравнительно невысокая скорость передачи (около 2 Мбит/с), что делает их пригодными для организации связи между АТС по обычным городским и сельским линиям связи, образующим довольно обширную сеть магистралей.
131
Скорость передачи по линиям связи более высокой иерархии увеличивается до 8 Мбит/с (цифровой поток Е2). В этом случае происходит мультиплексирование (объединение 4 потоков Е1. Аппаратура, осуществляющая это объединение, называется по числу образованных каналов – ИКМ-120. Скорость потока на выходе этой аппаратуры 8,448 Мбит/с.
Для образования высокоскоростных потоков объединяют цифровые потоки четырех систем ИКМ-120 (поток Е3). В результате скорость передачи в линии возрастает до 34,368 Мбит/с. Число каналов в новой системе равно 480, поэтому она получила название ИКМ-480.
Поступая далее аналогичным образом, получаем при слиянии четырех потоков систем передачи ИКМ-480 суммарный цифровой поток со скоростью 139,264 Мбит/с (цифровой поток Е4). Это уже аппаратура ИКМ-1920. На этом иерархия цифровых систем передачи не заканчивается. Можно про-
должать укрупнять потоки и дальше. |
|
|
|
|
|
|
Р |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
кбит/с |
|
|
|
|
|
|
|
|
|
|
|
И |
|||
|
|
|
64,0 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
У |
|
|
||||
1 |
|
|
|
Мбит/с |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
2,048 |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
2 |
|
|
|
|
|
|
|
|
|
|
Г |
|
|
|
||||
|
|
|
|
|
|
|
Мбит/с |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
3 |
|
|
ИКМ-30 |
2,048 |
|
|
|
8,448 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
Мбит/с |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
8,448 |
|
|
Б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
2,048 |
|
ИКМ-120 |
|
аИКМ-480 |
34,368 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
30 |
|
|
2,048 |
|
|
|
8,448 |
|
34,368 |
|
|
|
|
Мбит/с |
||||
|
. . . |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
к |
|
|
|
|
|
|
139,264 |
||||
|
|
64,0 |
|
|
|
|
|
34,368 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
8,448 |
|
|
|
|
|
ИКМ-1920 |
|
||
|
|
|
|
|
|
|
|
е |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
34,368 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
Рис. 9.5. Иерархия плезиохронных цифровых систем передачи |
||||||||||||||
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Принципыисинхронизации остаются неизменными для систем передачи |
||||||||||||||||
всех ступенейблиерархии, сколько бы их не было: точно так же выделяются из ц фрового потока тактовые импульсы и точно так же для обеспечения синхронной (а если точнее, синфазной) работы мультиплексоров и демульти-
Бплексоровипосылаются в линию комбинации импульсов цикловой синхронизации. Правда, некоторые отличия все же есть. О них и пойдет речь дальше.
Дело в том, что в системах передачи, начиная со второй ступени иерархии (это аппаратура ИКМ-120, ИКМ-480, ИКМ-1920 и т.д.), объединение потоков выполняется по принципу чередования битов (на рис. 9.6) дан пример объединения двух потоков). Таких потоков – четыре, и скорость каждого из них 2,048 Мбит/с. Четыре «двери» мультиплексора передающей станции поочередно открываются и пропускают в линию по одному биту из каждого цифрового потока. Разумеется, что они должны успеть это сделать за время,
132

пока данные биты не успели смениться следующими. Затем все снова повторяется.
|
1 |
|
|
0 |
|
|
0 |
|
1 |
|
|
1 |
|
1 |
|
|
|
0 |
|
|
|
1 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0 |
0 |
|
1 |
|
0 |
1 |
|
1 |
0 |
1 |
|
0 |
1 |
|
1 |
|
0 |
1 |
1 |
|
0 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Р |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
1 |
|
|
1 |
|
0 |
|
|
0 |
|
1 |
|
|
|
1 |
|
|
|
0 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
|
|||||||
|
|
Рис. 9.6. Мультиплексирование двух потоков |
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
по принципу чередования бит |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Г |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
|
|
|||||
Понятно, что объединение потоков становится возможным только за |
|||||||||||||||||||||||||||||||||
счет укорочения |
|
в |
|
|
4 |
|
раза |
|
длительности |
передаваемых импульсов, |
|||||||||||||||||||||||
т. е. фактически за счет уменьшения в 4 раза времени передачи каждого из них. Но как же в этом случае ввести в цифровой поток сигнал цикловой синхронизации, ведь места-то для него нет? Вероятно, путь только один – укоро-
тить информационные импульсы еще чуть-чуть. Пусть они немного «потес- |
|
нятся», тогда в цикле передачи появятсяа«пустые» временные интервалы, в |
|
которые и можно будет вставлять синхросигнал. |
|
|
к |
Вот как это делается |
ски. Приходящие на вход системы пере- |
дачи биты из четырех информационныхепотоков записываются в ячейки па- |
|
мяти ЗУ, а затем считываю ся с них и направляются в линию. Зачем так де-
лать? Казалось бы, |
не изменилось, только усложнилась аппаратура. |
|
практич |
Но это не так. Поск льку шины записи и считывания ЗУ независимы друг от |
|
друга, становится возможнымозаписывать биты с одной скоростью, а считы- |
|
вать – с другой, чуть чаще. «Прочитали» содержимое ячеек памяти быстрее – |
||
|
|
ничего |
вот и появи ась во времени «дырка» для вставки синхроимпульсов (рис. 9.7). |
||
Если |
лсчитывания не «отстают» и не «убегают вперед», а «идут» |
|
|
б |
|
|
импульсы |
|
весьма ста льно, то в каждом потоке регулярно появляются «пустые» интервалыБ. В с стеме передачи ИКМ-120 таким «пустым» интервалом, не несущим никакой информации, является во всех потоках каждый 33-й интервал. При объединении потоков в линию поочередно посылаются импульсы каждого из них, а так как на указанных «пустых» интервалах ни в одном из потоков никаких информационных импульсов нет, то в общем потоке периодически образуются «дырки» шириной в четыре интервала. В них-то и «вставляют» синхроимпульсы, а также другую служебную информацию. Напомним, что строгая периодичность синхросигнала – это одно из важнейших свойств, используемое для его распознавания.
133
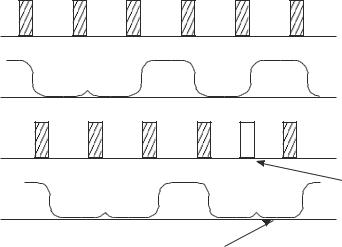
Импульсы
записи
Биты в ячейках |
1 |
0 |
0 |
1 |
0 |
1 |
|
1 |
|
памяти |
|
||||||||
|
|
|
|
|
|
|
|
||
Импульсы |
|
|
|
|
|
|
|
|
|
считывания |
|
|
|
|
|
|
|
|
|
Считываемый |
|
|
|
|
|
|
|
Лишний |
|
1 |
0 |
0 |
1 |
0 |
? |
1 |
импульс |
||
цифровой поток |
|||||||||
Р |
|||||||||
|
|
|
|
|
|
|
|||
|
|
|
«Пустой» временной |
|
|||||
|
|
|
|
интервал |
И |
||||
|
|
|
|
|
|
|
|||
Рис. 9.7. Формирование «пустых» интервалов в цифровом потоке |
|||||||||
|
|
|
|
|
Г |
|
|
|
|
Совсем иная картина будет наблюдаться, если местный генератор ока- |
|||||||||
|
|
|
|
Б |
|
|
|
||
жется не очень стабильным. В этом случае главные «часыУ» цифровой систе-
мы передачи (тактовые импульсы) могут «отставать» или «убегать вперед» по сравнению с их нормальным «ходом». В свою очередь, это будет вызывать смещение во времени «пустых» интерв лов в каждом цикле передачи, и, значит, нарушится строгая периодичность их повторения. На каком-то этапе
процедура реализована прак ич ски во всех современных системах передачи
может произойти полный сбой в |
|
системы синхронизации и, как след- |
|
а |
|
ствие, – всей аппаратуры в ц лом. Чтобы такого не случилось, местные «ча- |
||
|
к |
|
сы» (тактовые импульсы) нужно систематически «подводить». Подобная |
||
работе |
|
|
т |
|
|
высших (начиная со ) иерархий и называется «согласованием», а ино-
гда «выравниванием», ск р с ей цифровых потоков, или скоростей следования тактовых импульс в записи и считывания.
Как же все пр |
сх дит? Специальное устройство следит за взаимным |
|
|
|
второй |
положением импу ьсов записи и считывания. Пусть расстояние между со- |
||
седними парами |
|
импульсов постепенно начинает уменьшаться. Значит, |
|
этих |
|
л |
|
|
б |
|
|
местный генератор ускорил свой бег и импульсы считывания начали следо- |
||
вать быстрее. Как только контролируемый интервал уменьшится до критиче- |
||
скойивел ч ны, наш строгий «контролер» подаст сигнал тревоги: «пустой» Бинтервал появился раньше времени. Поскольку ему еще не время появляться, другое устройство введет в этот пустой интервал ложный импульс, не несущий никакой информации. Все происходит так же, как и в случае с нашими часами, когда, подводя их вперед, мы добавляем потерянные секунды. Вот и здесь мы тоже добавляем как бы потерянный импульс. Так достигается согласование, или выравнивание, скоростей записи и считывания цифровых потоков, которое в данном случае называется положительным (рис. 9.8).
Почему же обязательно нужно вставлять ложный импульс, не лучше ли взять да и притормозить чуть-чуть генератор тактовых импульсов? Дело в
134
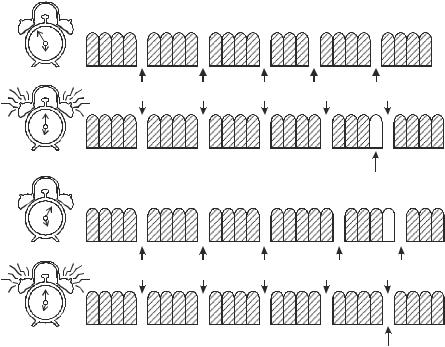
том, что тактовые импульсы разных цифровых потоков могут, в принципе, и не совпадать точно друг с другом, а генератор – один на всю систему передачи. Представим, что будет, если начать его непрерывно подстраивать то под один цифровой поток, то под другой. Тут единственный путь – вставлять по мере необходимости в каждый из потоков ложные импульсы.
В американской технической литературе описанная выше процедура согласования скоростей называется коротко одним словом: «staffing», что порусски произносится как «стаффинг», а переводится как «вставка».
После того как в цифровой поток введен ложный импульс, нужно пе-
редать на приемную станцию команду: «Внимание! Произошло согласование
один из «законных» пустых интервалов, не занятый синхроимпульсомР. Итак, если на приемной стороне в служебном интервале объединенного цифрового
скоростей». Она служит сигналом для ликвидации на приеме ложного им-
пульса. Такой командой может служить, например, посылка по служебному
каналу единичного бита. В качестве служебного канала можно использовать
потока появляется 1, это означает, что из выделенного низкоскоростного по- |
|||||||||||||||
тока нужно исключить очередной импульс – он ложный. |
|
И |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
||
|
12 |
|
|
|
|
|
|
|
|
|
|
Г |
|
||
9 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
Б |
|
Запись отстает |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
6 |
|
|
|
|
|
|
|
|
|
|
|
от считывания |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
«Пустые» интерв лы |
|
|
|
|
||||
|
12 |
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
9 |
|
3 |
|
|
|
|
|
|
|
|
|
Положительное |
|||
|
6 |
|
|
|
|
|
|
|
|
к |
|
|
согласование |
||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
Вс авлен ложный импульс |
|
|
||||
|
|
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
т |
|
|
|
|
|
|
|
9 |
|
3 |
|
|
|
|
|
|
|
|
|
Запись опережает |
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
6 |
|
|
|
|
|
|
|
|
|
|
считывание |
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
«Пустые» интервалы |
|
|
|
|
||||
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
||
|
12 |
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
9 |
|
3 |
|
|
|
|
|
|
|
|
|
Отрицательное |
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
л |
|
|
|
|
|
|
|
согласование |
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
б |
Исключѐн информационный импульс |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
и |
Рис. 9.8. Согласование скоростей цифровых потоков |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
Посылать по линии команду, состоящую всего из одного бита, является |
|||||||||||||||
крайнеБнеэффективным. Под воздействием помех 1 может превратиться в 0, а |
|||||||||||||||
0 в 1, и тогда случится непоправимое – информация будет декодирована неправильно. Поэтому для большей надежности команду согласования скоростей многократно дублируют, например, посылая ее 3 раза. В данном случае она будет иметь вид 111. Теперь, если в ней после воздействия помех останется только одна 1, команда все равно будет воспринята. Комбинация же
135
000 говорит о том, что согласование скоростей не производилось и пока все идет нормально.
До сих пор речь шла о том, что местный генератор может только «убежать вперед». Но с таким же успехом он может и «отставать», вырабатывая импульсы считывания реже, чем необходимо. Может случиться так, что в цифровом потоке уже должен появиться «пустой» интервал, а тактовые импульсы из-за замедленной их скорости до сих пор еще не считали из ЗУ предшествующий ему информационный импульс. Что делать в таком случае? Придется исключить из цифрового потока этот бит и предоставить временной интервал «по расписанию» для передачи очередной порции служебной информации (скажем, синхроимпульса). Только так можно согласовать, или выровнять, скорости тактовых импульсов записи и считывания. Такое согласование получило название отрицательного (см. рис. 9.8).
Если местные «часы» системы передачи (тактовые импульсы) подво- |
|
|
Р |
дятся и в ту, и в другую сторону, то одной команды: «Внимание! Произошло |
|
И |
|
У |
|
согласование скоростей» будет мало. Нужно еще сообщить на приемную |
|
станцию, какое согласование произошло: положительное или отрицательное, |
|
вводят команду «Вид согласования», посылая по другомуГслужебному каналу 1 при положительном согласовании и 0 – при отрицательном. Для надеж-
вставлен ложный импульс или исключен информационный. Для этой цели
ности ее также повторяют 3 раза. Комбин цияБ111 во втором служебном канале (организованном также за счет ч сти «пустых» интервалов) будет вос-
принята как сигнал о том, что в цифровой поток вставлен ложный импульс, а |
||
остальные «погибнут» в борьбепомехамис |
. |
|
комбинация 000 – что из потока «вырзан» информационный бит. Устрой- |
||
ства распознавания команд выполнкны таким образом, что они сработают |
||
|
т |
|
даже в том случае, если в командах «выживут» всего по одному биту, а |
||
Исключенный при передаче информационный бит также посылают по |
||
и |
|
|
третьему служебному каналу, причем для верности тоже повторяют 3 раза. Итак, приемник ц фр в й системы передачи по первой команде (комбинация 111) узнает, что прозошло согласование, по второй команде поймет, что нужно или иквидировать ложный импульс (комбинация 111), или восстано-
вить пропущенный информационный (комбинация 000), а по информации, |
|
взятой |
третьеголслужебного канала, определит, какой бит пропущен – 1 |
(комб нац я 111) или 0 (комбинация 000). |
|
|
б |
Объед нение потоков с выравниванием скоростей получило название |
|
из |
|
Б |
|
плезиохронного (почти синхронного), а существующая иерархия скоростей передачи цифровых потоков, а значит, и систем передачи типа ИКМ – плезиохронной цифровой иерархией (в англоязычном написании Plesiohronous
Digital Hierarhy – PDH).
Плезиохронная цифровая иерархия была разработана в начале 80-х годов прошлого столетия. На системы передачи данной иерархии возлагались большие надежды. Однако она оказалась очень негибкой: чтобы вводить в
цифровой поток высокоскоростной или выводить из него низкоскоростные потоки, необходимо полностью «расшивать», а затем снова «сшивать» высо-
136

коскоростной поток. Это требует установки большого числа мультиплексоров и демультиплексоров. Ясно, что выполнять эту операцию часто весьма дорого. На рис. 9.8 показана операция выделения потока со скоростью 2 Мбит/с из PDH потока со скоростью 140 Мбит/с.
В этом случае пришлось один поток со скоростью 140 Мбит/с демультиплексировать в четыре потока со скоростями 34 Мбит/с; затем один поток в 34 Мбит/с – в четыре потока 8 Мбит/с и только после этого «расшить» один поток 8 Мбит/с на четыре потока со скоростями 2 Мбит/с. Только таким сложным путем можно вывести или ввести поток пользователя в PDH-
системах передачи. |
Р |
|
Недостатком систем передачи плезиохронной цифровой иерархии является также то, что при нарушении синхронизации группового сигнала вос-
становление синхронизации первичных цифровых потоков происходит мно- |
||||||||||||||||||||||||||||||
гоступенчатым путем, а это занимает довольно много времени. |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
|||||
|
|
|
|
|
|
|
|
|
|
|
34 Мбит/c |
|
|
|
|
|
|
|
|
|
И |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Г |
|
|||||||
|
|
|
|
140 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
140 |
|
|||||
|
|
140 Мбит/c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
140 Мбит/c |
|
|
|
|
|
|
|
|
|
|
|
|
8 Мбит/c |
|
|
Б |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
34 |
|
34 |
|
|
|
|
|
|
|
|
|
|
|
34 |
|
|
|
34 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
2 Мбит/c |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
а |
|
8 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
к |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 Мбит/c |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
Пользоват ль |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Рис. 9.9. Выделение сигнала со скоростью 2 Мбит/с из плезиохронного циф- |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
рового по ока 140 Мбит/с |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
кбит |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
В настоящее время среди систем передачи PDH «выживают» только |
||||||||||||||||||||||||||||
системы первого ур вня |
|
ерархии, снабженные новой аппаратурой так назы- |
||||||||||||||||||||||||||||
|
|
л |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
ваемого гибкого му ьт |
плексирования, |
|
которая обеспечивает кроссовые со- |
|||||||||||||||||||||||||||
|
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
единения кана ов 64 |
|
|
/с; выделение и ввод отдельных каналов 64 кбит/с в |
|||||||||||||||||||||||||||
любом на оре; по ьзовательские интерфейсы от двухпроводных окончаний для телефонаидо окончаний базового доступа в цифровую сеть с интеграцией услуг; в деоконференц-связь и многое другое.
БНо самое главное, что заставило уже в середине 80-х годов XX в. искать новые подходы к построению цифровых иерархий систем передачи, это почти полное отсутствие возможностей автоматически контролировать состояние сети связи и управлять ею. А без этого создать надежную сеть связи с высоким качеством обслуживания практически невозможно. Все эти факторы и побудили разработать еще одну цифровую иерархию.
137

9.2.4. Синхронная цифровая иерархия
Синхронные транспортные модули. Новая цифровая иерархия была за-
думана как скоростная информационная автострада для транспортирования цифровых потоков с разными скоростями. В этой иерархии объединяются и разъединяются потоки со скоростями 155,520 Мбит/с и выше. Поскольку способ объединения потоков был выбран синхронный, то данная иерархия получила название синхронной цифровой иерархии (Synchronous Digital
Hierarchy – SDH).
Для передачи цифрового потока в SDH генерируются синхронные |
|
транспортные модули. |
Р |
|
|
Важной особенностью SDH является то, что в заголовках, помимо |
|
|
И |
маршрутной информации, наличествуют данные, позволяющие обеспечить |
|
управление всей сетью в целом, обеспечивать дистанционные переключения |
|
|
У |
в мультиплексорах, реализовывать эффективность эксплуатации сети и со- |
|
хранять качество на должном уровне. |
Г |
Для транспортирования цифрового потока со скоростью 155 Мбит/с создается синхронный транспортный модуль (Synchronous Transport Module) STM-1. Его упрощенная структура дана на рис. 9.10.
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
9 байт |
|
|
|
|
|
261 бБйт |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
к |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
3 |
|
RSOH |
|
|
|
|
|
|
|
||
строки |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
е |
|
|
|
|
|
1строка |
|
PTR |
|
|
|
|
|
||||||
|
|
|
9 |
||||||||||
|
|
|
|
|
о |
|
Полезная нагрузка |
строк |
|||||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
и |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
5 |
|
MSOH |
|
|
|
|
|
|
|
||
|
строк |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б |
|
|
|
|
Цикл передачи рамки 125 мкс |
|
|
|||||
и |
|
|
|
|
|
|
|
|
|||||
|
лРис. 9.10. Структура синхронного транспортного модуля |
||||||||||||
|
|
|
|||||||||||
БМодуль представляет собой фрейм (рамку) 9 270 = 2430 байт. Кроме передаваемой информации (называемой в литературе полезной нагрузкой), он содержит в 4-й строке указатель (Pointer, PTR), определяющий начало записи полезной нагрузки.
Чтобы определить маршрут транспортного модуля, в левой части рамки записывается секционный заголовок (Section Over Head – SOH). Нижние 5 9 = 45 байт (после указателя) отвечают за доставку информации в то место сети, к тому мультиплексору, где этот транспортный модуль будет переформировываться. Данная часть заголовка так и называется: секционный заголовок мультиплексора (MSOH). Верхние 3 9 = 27 байт (до указателя) представ-
138
ляют собой секционный заголовок регенератора (RSOH), где будут осуществляться восстановление потока, «поврежденного» помехами, и исправление ошибок в нем.
Один цикл передачи включает в себя считывание в линию такой прямоугольной таблицы. Порядок передачи байт – слева направо, сверху вниз (так же, как при чтении текста на странице). Продолжительность цикла передачи STM-1 составляет 125 мкс, т.е. он повторяется с частотой 8 кГц. Каждая клеточка соответствует скорости передачи 8 бит 8 кГц = 64 кбит/с. Значит, если тратить на передачу в линию каждой прямоугольной рамки 125 мкс, то
за секунду в линию будет передано 9 270 64 кбит/с = = 155520 кбит/с, т.е. |
|
155 Мбит/с. |
Р |
|
|
Для создания более мощных цифровых потоков в SDH-системах фор- |
|
|
И |
мируется следующая скоростная иерархия (табл. 9.3): 4 модуля STM-1 объединяются путем побайтового мультиплексирования в модуль STM-4, передаваемый со скоростью 622,080 Мбит/с; затем 4 модуля STM-4 объединяют-
ся в модуль STM-16 со скоростью передачи 2488,320 Мбит/с; наконец, 4 мо- |
|||||||||
дуля STM-16 могут быть объединены в высокоскоростной модуль STM-64 |
|||||||||
(9953,280 Мбит/с). |
|
|
|
|
|
|
У |
||
|
|
|
|
|
|
|
Г |
Таблица 9.3 |
|
|
|
|
|
|
|
Б |
|
||
|
|
|
|
|
|
|
|
||
|
|
|
Синхронн я цифров я иерархия |
|
|||||
Уровень иерархии |
|
Тип синхронного тр нс- |
Скорость передачи дан- |
||||||
|
|
|
|
|
|
а |
|
ных, Мбит/с |
|
|
|
|
|
портного модуля |
|
||||
|
|
|
|
|
к |
|
|
|
|
1 |
|
|
|
|
STM-1 |
|
|
155,520 |
|
2 |
|
|
|
|
STM-4 |
|
|
622,080 |
|
|
|
|
|
е |
|
|
|
|
|
3 |
|
|
|
STM-16 |
|
|
2488,320 |
||
4 |
|
|
|
STM-64 |
|
|
9953,280 |
||
|
|
|
т |
|
|
|
|
|
|
Мультиплекс р ван е происходит по следующей схеме: сначала |
|||||||||
|
|
о |
|
|
|
|
|
|
|
каждые 4 моду я STM-1 с помощью мультиплексоров с четырьмя входами |
|||||||||
объединяются в модуиь STM-4, затем четыре модуля STM-4 мультиплек- |
|||||||||
сируются таким же 4-входовым мультиплексором в модуль STM-16. Сле- |
|||||||||
|
л |
|
|
|
|
|
|
|
|
дует отмет ть, что существует мультиплексор на 16 входов, с помощью |
|||||||||
которого можно одновременно объединить 16 модулей STM-1 в мо- |
|||||||||
б |
|
|
|
|
|
|
|
|
|
дуль STM-16. |
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
Формирование модуля STM-1. В сети SDH применены принципы кон- |
|||||||||
тейнерныхБ перевозок. Подлежащие транспортировке сигналы предварительно размещаются в стандартных контейнерах (Container – С). Все операции с контейнерами производятся независимо от их содержания, чем и достигается прозрачность сети SDH, т. е. способность транспортировать различные сигналы, в частности, сигналы PDH.
Наиболее близким по скорости к первому уровню иерархии SDH (155,520 Мбит/с) является цифровой поток со скоростью 139,264 Мбит/с, образуемый на выходе аппаратуры плезиохронной цифровой иерархии ИКМ-
139
1920 (использует поток Е4). Его проще всего разместить в модуле STM-1. Для этого поступающий цифровой сигнал сначала «упаковывают» в контейнер (т. е. размещают на определенных позициях его цикла), который обозначается С-4.
Рамка контейнера С-4 содержит 9 строк и 260 однобайтовых столбцов. Добавлением слева еще одного столбца – маршрутного или трактового заголовка (Path Over Head – РОН) – этот контейнер преобразуется в виртуальный контейнер VC-4.
|
Наконец, чтобы поместить виртуальный контейнер VC-4 в модуль |
|
STM-1, его снабжают указателем (PTR), образуя таким образом администра- |
||
|
|
Р |
тивный блок AU-4 (Administrative Unit), а последний помещают непосред- |
||
ственно в модуль STM-1 вместе с секционным заголовком SOH (рис. 9.11 и |
||
9.12). |
И |
|
|
|
|
|
Синхронный транспортный модуль STM-1 можно загрузить и плезио- |
|
|
У |
|
хронными потоками со скоростями 2,048 Мбит/с. Такие потоки формируются |
||
аппаратурой ИКМ-30, они широко распространены в современных сетях. Для первоначальной «упаковки» используется контейнер С12. Цифровой сигнал размещается на определенных позициях этого контейнера. Путем добавления
маршрутного, или транспортного, заголовка (РОН) образуется виртуальный |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Г |
|
|
|
контейнер VC-12. Виртуальные контейнеры формируются и расформировы- |
||||||||||||||||||||
ваются в точках окончаниях трактов. |
|
Б |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
STM-1 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
261 байт |
|
AU-4 |
|
|
|
||
|
|
|
|
|
|
RSOH |
|
|
|
|
|
к |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
1 |
е |
260 байт |
|
VC-4 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
байт |
|
|
|
|||||||
|
|
|
|
|
|
PTR |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
9 |
|
|
|
|
|
|
|
т |
|
|
|
|
260 байт |
C-4 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
строк |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
MSOH |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
P |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
Полезная |
|
|
|||
|
|
|
|
|
|
и |
|
|
|
O |
|
9 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
нагрузка |
|
|
||||||
|
|
|
|
|
|
|
|
|
H |
|
строк |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
л |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
Рис. 9.11. Преобразования потока Е4 в STM-1 |
|
|
|||||||||||||||
Б |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В модуле STM-1 можно разместить 63 виртуальных контейнера VC-12. При этом поступают следующим образом. Виртуальный контейнер VC-12 снабжают указателем (PTR) и образуют тем самым транспортный блок TU-12 (Tributary Unit). Теперь цифровые потоки разных транспортных блоков можно объединять в цифровой поток 155,520 Мбит/с (cм. рис. 9.12). Сначала три транспортных блока TU-12 путем мультиплексирования объединяют в груп-
140

пу транспортных блоков TUG-2 (Tributary Unit Group), затем семь групп |
|||||||||||||
TUG-2 мультиплексируют в группы транспортных блоков TUG-3, а три |
|||||||||||||
группы TUG-3 объединяют вместе и помещают в виртуальный контейнер |
|||||||||||||
VC-4. Далее путь преобразований известен. |
|
|
|
|
|
||||||||
На рис. 9.12 показан также способ размещения в STM-1 трех потоков |
|||||||||||||
от аппаратуры плезиохронной цифровой иерархии ИКМ-480 (34,368 Мбит/с). |
|||||||||||||
Плезиохронные цифровые потоки всех уровней размещаются в контей- |
|||||||||||||
нерах С с использованием процедуры выравнивания скоростей (положитель- |
|||||||||||||
ного, отрицательного и двухстороннего). |
|
|
|
|
|
|
|||||||
Наличие большого числа указателей (PTR) позволяет совершенно чет- |
|||||||||||||
ко определить местонахождение в модуле STM-1 любого цифрового потока |
|||||||||||||
со скоростями 2,048; 34,368 и 139,264 Мбит/с. Выпускаемые промышленно- |
|||||||||||||
стью мультиплексоры ввода–вывода (Add/Drop Multiplexer-ADM) позволяют |
|||||||||||||
ответвлять и добавлять любые цифровые потоки. |
|
|
|
Р |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
155,520 Мбит/c |
|
|
|
|
|
|
|
139,264 Мбит/c |
|||||
|
STM-1 |
|
AU-4 |
|
VC-4 |
|
|
|
|
|
|
И |
|
|
|
|
|
|
|
|
|
У |
C-4 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
||
155,520 Мбит/c |
|
|
|
|
|
|
|
34,368 Мбит/c |
|||||
|
|
|
|
|
|
|
|
|
|
Г |
|
|
|
|
STM-1 |
|
AU-4 |
|
VC-4 |
|
TUG-3 |
|
TU-3 |
|
VC-3 |
|
C-3 |
|
|
|
|
|
|
x3 |
|
|
Б |
|
|
|
|
155,520 Мбит/c |
|
|
TUG-а3 TUG-2 |
|
2,048 Мбит/c |
||||||||
|
|
|
|
||||||||||
|
STM-1 |
|
AU-4 |
|
VC-4 |
|
|
TU-12 |
|
VC-12 |
|||
|
|
|
|
|
|
x3 |
к |
|
x3 |
|
|
|
|
|
|
|
|
|
|
|
x7 |
|
|
|
C-12 |
||
|
|
|
|
|
|
е |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
Рис. 9.12. Размещение по оков Е1, Е3 и Е4 в контейнере STM-1 |
|||||||||||||
Важной особенн стью аппаратуры SDH является то, что в тракто- |
|||||||||||||
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
вых и сетевых заг л вках п мимо маршрутной информации создается |
|||||||||||||
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
много информац , позволяющей обеспечить наблюдение и управление |
|||||||||||||
всей сетью в це ом, дистанционные переключения в мультиплексорах по |
|||||||||||||
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
требованию к иентов, осуществлять контроль и диагностику, своевре- |
|||||||||||||
|
|
л |
|
|
|
|
|
|
|
|
|
|
|
менно о наруживать и устранять неисправнссти, реализовать эффектив- |
|||||||||||||
ную эксплуатацию сети и сохранить высокое качество предоставляемых |
|||||||||||||
услуг. |
б |
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
Б9.2.5. Методы асинхронной передачи |
|
|
|
|
|
||||||||
В последнее десятилетие к передаче информации стали предъявляться более широкие требования. Одному и тому же абоненту могут быть переданы различные по характеру сообщения: движущиеся изображения (видеотелефон, видеоконференция); компьютерные данные (файлы); электронная почта; информация из системы дистанционного обучения (в том числе муль-
141
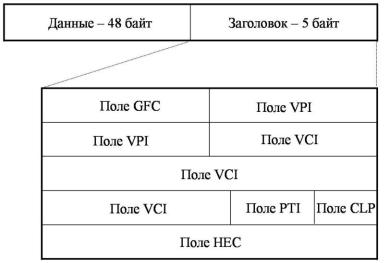
тимедийная); фильмы по кабельному телевидению и др. Причем источники этой информации являются, как правило, асинхронными. Информация от одних источников может поступать непрерывно, от других – время от времени. Скорость поступления информации от различных источников различная. Так, речевой поток поступает со скоростью 64 кбит/с, а передача движущегося изображения требует скорости от 1,5 до 100 Мбит/с.
Для согласования всех этих различных требований в 1980–1990-х гг. была предложена новая технология передачи, получившая название моды асинхронной передачи (Asynchronous Transfer Mode – ATM). Асинхронный
режим передачи (Asynchronous Transfer Mode, ATM, МАП в русской тран-
менялись для передачи информации, когда задержки сигнала нежелательныР ; сети с коммутацией пакетов применялись в случае, когда некоторые задерж-
скрипции) – сетевая технология, предоставляющая возможность передавать данные, оцифрованную видео- и аудиоинформацию, а также изображения.
Пользователь сам выбирал тип сети: сети с коммутацией каналов при-
ки допустимы. АТМ объединяет в себе преимущества первой и второй тех- |
||||||||||
нологий. |
|
|
|
|
|
|
|
|
|
И |
|
|
|
|
|
|
|
|
|
|
|
В основе технологии АТМ лежит передача данных в виде ячеек фикси- |
||||||||||
|
|
|
|
|
|
|
|
|
У |
|
рованной длины (53 байта) главным образом из одной локальной сети в дру- |
||||||||||
|
|
|
|
|
|
|
|
Г |
|
|
|
|
|
|
|
|
|
|
Б |
|
|
гую с помощью глобальной сети. Эта технология предполагает запись любо- |
||||||||||
|
|
|
|
|
|
|
а |
|
|
|
го вида информации в ячейки (Cells) фиксированной длины. Ячейки содер- |
||||||||||
|
|
|
|
|
|
к |
|
|
|
|
жат (рис. 9.13) полезную информацию и з головок (Header). |
|
|||||||||
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
л |
|
|
|
|
|
|
|
|
|
б |
|
|
|
|
|
|
|
|
|
|
и |
|
|
Рис. 9.13. Структура ATM-ячейки |
|
||||||
БПоле GFC (Generic Follow Control) занимает первые 4 байта и предна- |
||||||||||
значено для управления потоком между АТМ-сетью и пользователями. |
||||||||||
Поле VPI |
(Virtual Path Identifier) определяет виртуальный маршрут, |
|||||||||
представляющий собой набор каналов, по которым передается информация (длина 8 бит или 12 бит, в зависимости от используемого интерфейса).
142
Второй частью идентификатора соединения является поле VCI (Virtual Channel Identifier). Имеет длину 16 бит и предназначено для идентификации соединения двух АТМ-станций.
Поле PTI (Payload Type Identifier – идентификатор полезной нагрузки) имеет длину 3 бита и определяет тип информации, передаваемой АТМ ячейкой (управляющая или данные).
Значение в поле CLP (Cell Loss Priority – приоритет ячейки) имеет длину 1 бит и определяет относительный приоритет данных, передаваемых в ячейке.
В поле HEC (Header Error Control), имеющее длину 8 бит, записывается |
|
|
Р |
результат контроля ошибок в заголовке, вычисленный с помощью цикличе- |
|
ского избыточного кода (CRC). |
И |
Цифровая информация от источников сообщений заполняет ячейки. |
|
Поскольку ячейки имеют фиксированную длину, то нет необходимости отде-
появляющиеся через большие временные интервалыГ, могутУбыть собраны для наполнения ячеек либо могут передаваться в отдельных ячейках. В последнем случае в полупустые ячейки добавляется «наполнитель». Ячейки
лять их друг от друга (т. е. определять их начало и конец) с помощью слу-
жебной информации. Если у источника отсутствует потребность в передаче
информации, то передаются пустые ячейки. Небольшие объемы информации,
рабатывать при прохождении через коммутатор. Прочитав идентификатор канала в заголовке ячейки, коммутатор переправляет ее из одного порта в другой вне зависимости от той информации, которая находится в ячейке.
формируются источниками по мере потребности. В случае непрерывной пе- |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|||||||||||||
редачи (речь, видеоконференция и т. п.) ячейки следуют через строго опреде- |
||||||||||||||||||||||||||||||||||
ленное время. |
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
Поток А |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
к |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Поток B |
|
|
|
|
|
|
|
|
|
|
|
A C A A B A B C |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Муль и- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
плексор |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Поток C |
|
|
|
|
|
|
т |
|
|
|
|
|
|
Поток ячеек в |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
соединительном кабеле |
|||||||||||||||||
|
|
|
|
|
|
|
|
о |
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Р с. 9.14. Структура ATM-ячейки |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
ячеек от различных источников могут быть объединены с по- |
|||||||||||||||||||||||||||||
|
|
|
|
л |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
мощью временного мультиплексирования (рис. 9.14). |
||||||||||||||||||||||||||||||||||
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Пре муществом МАП-ячеек является то, что их очень легко об- |
||||||||||||||||||||||||||||||||||
Потоки |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Коммутатор может переключать целые группы виртуальных каналов, не проводя анализа информации по каждому каналу в отдельности. Для этого несколько виртуальных каналов, проходящих по одному и тому же направлению на каком-либо участке сети связи, объединяют в виртуальный путь. VCI и VPI образуют уникальный индивидуальный адрес маршрута на каждом отдельном участке сети. Изменение идентификаторов может происхо-
143
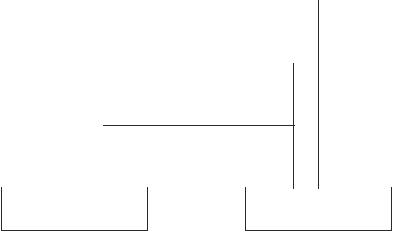
дить в каждом промежуточном коммутаторе. Назначение маршрута передачи ячеек может быть осуществлено оператором сети или сигнальной системой.
Технология АТМ имеет свою эталонную модель по аналогии с 7-уровневой моделью взаимодействия открытых систем (OSI – Open System Interconnection).
Основу эталонной модели АТМ составляют физический уровень, уровень АТМ и уровень адаптации АТМ (рис. 9.15). В АТМ фактически физический уровень не определяется – при создании данной технологии изначально была предусмотрена возможность ее работы с различными средами.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Р |
|
|
Конечная точка АТМ |
|
|
|
|
|
Конечная точка АТМ |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
|
|
|
|
Уровень |
|
|
|
|
|
|
|
|
|
Уровень |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
У |
|
|
|
|
адаптации АТМ |
|
|
|
|
|
|
|
адаптации АТМ |
|
|||||
|
Уровень АТМ |
|
|
Уровень АТМ |
|
Г |
ровень АТМ |
|
|||||||
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Физический уровень |
|
а |
|
|
Физический уровень |
|||||||||
|
Физический уровень |
|
|
||||||||||||
|
|
|
|
|
|
|
к |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Набор АТМ-протоколов |
|
|
|
|
||||
|
|
|
|
|
Рис. 9.15. Э алонная модель АТМ |
|
|
|
|||||||
|
Технология |
АТМ |
х рошо согласуется с |
технологией SDH: |
|||||||||||
|
|
|
|
они |
|
|
|
|
|
|
|
|
|
||
МАП-ячейки могут бытьтп мещены в синхронный транспортный модуль |
|||||||||||||||
|
|
|
л |
осначала «упаковываются» в виртуальный контейнер |
|||||||||||
STM-1. Для этого |
|||||||||||||||
VC-4, а в заго овке (РОН) этого контейнера отмечается начало записи МАП- |
|||||||||||||||
|
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
ячеек (рис. 9.16). Затем контейнер, как обычно, помещается в модуль STM-1. |
|||||||||||||||
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
144
|
|
|
1 байт |
|
|
260 байт |
|
|
|
|||
|
|
|
|
|
|
|
|
|
VC-4 |
|
|
|
|
|
9 строк |
|
|
|
|
MАП-ячейки |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
POH |
|
Указатель расположения |
|
|
Р |
||||
|
|
|
VC-4 |
|
|
MАП-ячеек |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 9. 16. Размещение потоков ATM-ячеек в контейнере STM-1 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
И |
|
|
|
|
|
|
|
|
|
|
|
У |
|
|
|
|
|
|
|
|
|
|
|
Г |
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
|
|
|
|
|
к |
|
|
|
|
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
л |
|
|
|
|
|
|
|
|
|
|
|
б |
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
145 |
10. МОДУЛЯЦИЯ В ОСНОВНОЙ (ИНФОРМАЦИОННОЙ)
ПОЛОСЕ ЧАСТОТ (BASEBAND MODULATION)
10.1. Основные принципы модуляции
Для начала определим понятие «модуляция». В наиболее широком понимании модуляция это процесс изменения по заданному закону во времени величин, характеризующих какой-либо регулярный физический процесс.
Одна из особенностей информации как объекта заключается в ее взаи-
мосвязи с материальными объектами. Информация непосредственно связана
цесс информационной модуляции данных объектов. Таким образомР, информация вне материальных объектов не существует и ее передача возможна
с событиями, происходящими с реальными объектами, и таким образом,
наличие той или иной информационной нагрузки в процессах, происходящих
только посредством использования материального носителяИ. Применительно к технике электросвязи в качестве носителей выступают сигналы. В качестве
с материальными объектами, может, в общем случае, трактоваться как про-
первому относится так называемая BaseBand-модуляцияБ , или модуляция в основной полосе частот. Отличительная особенность данного вида модуляции
данных сигналов используется электромагнитное поле в направляющих си- |
||
стемах (проводниках) или в пространстве. |
У |
|
Г |
||
|
||
Следует различать два вида модуляции, используемых в электросвязи. К |
||
заключается в том, что скорость измененияаво времени сигнала-переносчика соизмерима со скоростью изм н ния информации. В этом случае сигнал-
переносчик может ассоциироваться |
непосредственно с информацией. |
|
|
к |
|
Например, голосовое сообщ |
, носителем которого являются звуковые |
|
волны, непосредственно ассоциируетсяние |
с воспринимаемым звуком. Данное |
|
формационной пол сеочастт.
свойство позволяет называ ь э от вид модуляции также модуляцией в ин-
скорость измененлия которого во времени значительно превосходит скорость изменения информации. Данный вид информации получил название полосовой модуляции. Характерным примером полосовой модуляции являются ра-
Ко второму в ду м дуляции относится модуляция, использующая в качестве переносч ка нформационной составляющей физического носителя
диосигналыб, у которых сигнал-переносчик представляет собой гармоническое колебание, скорость изменения которого значительно выше модулирующей информационной составляющей.
Бвичная или «получающаяся сама собой» (информация как бы самостоятельно присоединяется к носителю), а полосовая модуляция – как вторичная, т. е. результат воздействия первично модулированных носителей информации на другие материальные объекты.
Модуляция в основной полосе частот может рассматриваться как пер-
Применительно к технике цифровой радиосвязи информация преобразуется в наборы символов, которые ассоциируются с конкретными сигналами (например, символ логической «1» связывается с высоким уровнем сигнала, а
146
символ логического «0» – с низким уровнем), таким образом происходит первичная модуляция или модуляция в основной полосе частот электрического сигнала.
Особенность систем электросвязи заключается в необходимости передачи информации на достаточно большие расстояния. Данная особенность накладывает определенные требования на сигналы-переносчики информации.
Применительно к сигналам, модулированным в основной полосе частот, к основным требованиям можно отнести:
1.Отсутствие постоянной составляющей в сигнале-переносчике информации.
2.Нечувствительность к смене «полярности» используемой линии передачи. Р
3.Простота и надежность восстановления информации на приемной стороне (высокая помехоустойчивость, простота процесса синхронизацииИи др.).
В системах цифровой связи сигналы с модуляцией в основной полосе частот часто называют кодами линии или линейными кодамиУ(не следует путать с линейными помехоустойчивыми кодами).
Коды линии можно условно разделить на две группыГ: сигналы с импульсной модуляцией (ИМ) и сигналы с импульсно-кодовойБмодуляцией (ИКМ).
К группе сигналов с импульсной модуляцией относятся сигналы,
сформированные в соответствии с методами, изложенными ниже.
Амплитудно-импульсная модуляция а(АИМ). Сигнал в этом случае пред-
ставляет собой последовательность импульсовкпостоянной длительности, следующих с фиксированной частотой. Информ ционн я составляющая закладывается
вамплитуду данных импульсов. е
лоб
Информационная составляющая закладывается в изменение временного положенБя мпульсов относительно опорного (синхронизирующего импульса).
Примечание. Указанные выше методы импульсной модуляции могут использоваться для переноса как непрерывной, так и дискретной (цифровой информации).
К группе сигналов с импульсно-кодовой модуляцией относятся сигналы, в которых информационная составляющая представляется сменой определенных кодовых последовательностей элементарных импульсов. При этом каждому информационному символу соответствует своя последовательность импульсов. Например, если информационные – это n -разрядные двоичные числа, то данные
147
последовательности, как правило, представляют собой комбинацию из n импульсов, представляющих логические символы «1» и «0».
В настоящее время в системах цифровой связи наиболее широкое распространение получили методы модуляции в основной полосе частот, основанные на ИКМ. Именно данные сигналы чаще всего называют кодами линии. Рассмотрим их более подробно.
10.2.1. Код без возвращения к нулю (NRZ)
Код без возвращения к нулю (NRZ – non-return-to-zero) является двоичным
кодом линии, в котором символ логической «1» кодируется одним уровнем, а |
|
|
Р |
символ логического «0» – другим уровнем. При кодировании кодом NRZ отсут- |
|
ствует третье (промежуточное, нейтральное состояние). |
И |
|
|
Код NRZ не относится к числу кодов, обеспечивающих тактовую самосин- |
|
хронизацию. Иными словами, для обеспечения тактовой синхронизации необхо- |
||||||
|
|
|
|
|
|
У |
|
|
|
|
|
Г |
|
|
|
|
|
Б |
|
|
дима реализация специальных мер по выделению тактовой частоты, поскольку в |
||||||
спектре сигнала с NRZ отсутствуют компоненты, представляющие тактовые им- |
||||||
пульсы. |
|
|
кода |
|
|
|
|
|
к |
|
|
|
|
Существует несколько разновидностей |
|
без возвращения к нулю: уни- |
||||
полярный код без возвращения к нулю (UNRZ); биполярный код без возвращения |
||||||
|
е |
|
|
|
|
|
к нулю (BNRZ); код без возвращ ния нулю с инверсией (NRZI). |
||||||
При кодировании UNRZ символ логической «1» кодируется высоким |
||||||
|
т |
|
|
|
|
|
уровнем, а символ логического «0» – низким уровнем. |
|
|||||
При кодировании BNRZ символ логической «1» кодируется высоким уров- |
||||||
нем, а символ логическ «0» – высоким уровнем другой полярности.
При кодировании NRZI при передаче логического «0» не происходит сме- |
|||||
|
|
|
при |
|
|
ны состояния кода, а |
|
передаче логической «1» происходит смена состояния |
|||
|
|
л |
го |
||
на противоположное. |
|||||
На рис. 10.1 пр веден пример кодирования последовательности двоичных |
|||||
|
б |
|
|
|
|
символов раз ичными разновидностями кода NRZ. |
|||||
и |
|
|
|
|
|
Б |
|
|
|
|
|
10.2.2. Манчестерский код (Manchester code)
Манчестерский код является бинарным кодом линии, в котором во время передачи информационного символа происходит по крайней мере одно изменение состояния. Данный код может рассматриваться как фазовая манипуляция некоторого колебания в виде меандра потоком информационных символов. Чаще всего в качестве «несущего» колебания используется сигнал тактового генератора. Если поток данных и сигнал тактового генератора представлены в коде BNRZ,
148

то результат кодирования манчестерским кодом эквивалентен перемножению этих кодов (см. рис. 10.2).
Передаваемый |
Передаваемый |
Передаваемый |
Передаваемый |
||||
символ |
|
символ |
|
символ |
|
символ |
|
1 1 0 |
0 1 |
0 1 |
0 |
0 0 |
1 1 |
0 0 |
1 |
UNRZ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
Р |
||
BNRZ |
|
|
|
|
|
|
|
И |
|
|
|
|
|
|
|
|
|
|
У |
|
t |
||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
Г |
|
|
|
|
|
UNRZI |
|
|
|
|
|
Б |
|
|
|
t |
|
|
|
|
|
|
а |
|
|
|
|
|
|
|
|
|
|
к |
|
|
|
|
|
|
|
BNRZI |
|
|
е |
|
|
|
|
|
|
|
|
|
|
т |
|
|
|
|
|
|
t |
||
|
|
|
|
|
|
|
|
|
|
||
|
о |
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
Рис. 10.1. Пр мер к дирования передаваемых символов кодом NRZ |
|||||||||||
Линейный манчестерский код не содержит постоянной составляющей и яв- |
|||||||||||
б |
|
|
|
|
|
|
|
|
|
|
|
ляется самосинхронизирующимся. Данный линейный код нашел широкое рас- |
|||||||||||
и |
|
|
|
|
|
|
|
|
|
|
|
пространение влсетях Ethernet и в системах радиочастотной идентификации RFID. |
|||||||||||
Б |
|
|
|
|
|
|
|
|
|
|
|
10.2.3. Код с возвращением к нулю (RZ) |
|
|
|
|
|
||||||
Код с возвращением к нулю (RZ – return-to-zero) является двоичным кодом линии, в котором символ логической «1» кодируется одним уровнем, а символ логического «0» другим уровнем. При кодировании кодом NRZ вводится третье промежуточное, нейтральное состояние (нуль). Переход от одного символа к другому осуществляется только через промежуточное состояние. Промежуточное состояние вводится для реализации возможности самосинхронизации. Как и код
149

NRZ, код с возвращением к нулю может быть униполярным и биполярным
(см. рис. 10.3).
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
Data
|
|
|
|
|
|
|
|
|
|
|
|
|
Р |
||
Clock |
|
|
|
|
|
|
|
|
И |
|
|||||
|
|
|
|
|
|
|
У |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
Г |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
к |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
|
|
|
|
|
о |
|
Manchester |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Рис. 10.2. Пример кодирования передаваемых символов манчестерским кодом |
|||||||||||||||
|
|
|
|
и |
т1 |
|
|
|
|
|
|
|
|
||
|
|
|
|
0 1 |
0 0 1 |
|
0 |
0 |
|
||||||
б |
л |
|
|
|
|
|
|
|
|
|
|
|
|||
URZ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
BRZ |
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
Рис. 10.3. Пример кодирования передаваемых символов кодом RZ
150
10.2.4.Код с чередующейся инверсией (AMI)
Код с чередующейся полярностью импульсов (ЧПИ) – Alternate Mark Inversion (AMI) – биполярный код, представляющий одну из разновидностей троичного кода: нулям соответствует отсутствие импульса, а единицам – попеременно чередующиеся прямоугольные импульсы отрицательной и положительной полярности. Так как постоянная составляющая импульсной последовательности равна нулю, то возможна передача по линиям, содержащим разделительные трансформаторы. Преимуществом данного кода является простота преобразова-
ния в двоичный код. |
|
Р |
|
|
|
AMI-код использует следующие представления символов (рис. 10.4): |
||
символы логического «0» представляются нулевым напряжением (0 В); |
||
|
И |
|
символы логической «1» представляются поочерѐдно значениями -U |
||
или +U (В). |
У |
|
AMI-код обладает хорошими синхронизирующими свойствами при пере-
лов) нулей в потоке данных, поскольку длинные последовательности нулей ведут к потере синхронизации.
даче серий единиц и сравнительно прост в реализации. Недостатком кода является ограничение на плотность (количество последовательноГпоявляющихся симво-
|
|
|
|
Передаваемый |
Передаваемый |
|
ПередБв емый |
Передаваемый |
||||||||
|
|
|
|
символ |
|
символ |
|
|
|
|
символ |
символ |
|
|
||
|
|
|
1 1 0 |
0 1 |
0 1 |
|
а1 1 |
0 0 |
1 |
|
||||||
|
|
|
|
|
||||||||||||
|
|
|
0 |
0 |
|
0 |
|
|
||||||||
|
|
|
|
|
|
|
|
к |
|
|
|
|
||||
|
AMI |
|
|
|
|
е |
|
|
|
|
|
|
|
|||
|
|
|
|
т |
|
|
|
|
|
|
|
t |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 10.4. Пример кодирования передаваемых символов кодом AMI |
|||||||||||||||
|
|
л |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
б |
Биполярный код высокой плотности порядка n (HDB-n) |
||||||||||||||
10.2.5. |
|
|
||||||||||||||
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Наиболее существенным недостатком кода с AMI является необходимость передачи по линейному тракту сигнала с длинными сериями нулей, что может нарушить нормальную работу регенераторов, так как затрудняется процесс выделения тактовой частоты. С целью устранения этого недостатка было разработано несколько модификаций кода с AMI, наибольшее распространение среди которых получил код HDB-n (наибольшее распространение получила версия HDB-3, принятая за стандартную для цифровых линий связи в Европе).
151

Принцип построения кода HDB-n такой же, как и кода с AMI, до тех пор, пока между двумя единичными символами не появится более n 1 следующих подряд нулевых символов. При этом каждая последовательность из n нулевых символов (00…00) в исходном двоичном коде заменяется одной из двух последовательностей из n 1 символов вида В0…0V или 00…0V, где B – импульс, по полярности противоположной предыдущему импульсу (отвечает правилу кодирования AMI), V (Violation) – импульс, по полярности соответствующий предыдущему импульсу (нарушающий правило кодирования AMI). Выбор замены (В0…0V или 00…0V) осуществляется таким образом, чтобы число импульсов B между двумя последовательно расположенными импульсами V было нечетным. На рис. 10.5 представлен пример кодирования в соответствии с правилами преобразования в HDB-3.
кода, что, в свою очередь, позволяет устранить влияние этих символов на среднее
|
Информационный |
|
Информационный |
Информационный |
нформационный |
||||||||||||
|
|
символ |
|
|
|
символ |
|
|
|
символ |
|
|
Р |
||||
|
|
|
|
|
|
|
|
|
|
символ |
|||||||
|
0 1 0 0 0 0 0 1 1 1 1 0 0 0 0 1 |
0 1 1 0 0 0 0 0 0 1 1 0 |
|
||||||||||||||
NRZ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
||
|
|
|
|
|
|
|
|
|
|
|
|
У |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
AMI |
|
|
|
|
|
|
|
|
|
|
Г |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
B 0 0 V |
|
|
|
B 0 0 |
V |
|
0 |
0 0 |
V |
|
|
|
|||
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
|
||
|
B |
|
B |
|
|
B |
B |
|
V |
B |
|
|
|
|
|
B |
|
HDB-3 |
|
|
|
|
|
|
к |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
V |
B |
|
B |
|
B |
|
B |
|
|
V |
|
B |
||
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 10.5. Пр мер ктдирования передаваемых символов кодом HDB-3 |
||||||||||||||||
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Испо ьзован е двух замещающих последовательностей обеспечивает че- |
|||||||||||||||||
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
редование по ярности символов V, появляющихся в различных местах линейного |
|||||||||||||||||
|
л |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
значение, которое так же, как и у кода AMI, оказывается равным нулю. Б
152
11.ПОЛОСОВАЯ МОДУЛЯЦИЯ/ДЕМОДУЛЯЦИЯ (модуляция/демодуляция радиосигналов)
11.1. Основные принципы полосовой модуляции
Для передачи информации на расстояние применяются сигналы, эффективно излучаемые с помощью антенных устройств, обладающие способностью распространяться в виде свободных радиоволн в среде, разделяющей отправителя и получателя информации. Такими сигналами являются высокочастотные колебания. Передаваемая информация должна быть тем или иным способом заложена в высокочастотное колебание, называемое несущим. Несущее колебание необязательно должно являться гармоническим. В качестве несущего колебания могут
использоваться квазигармонические («почти» или очень похожие на гармониче- |
||||
|
|
|
|
И |
ские) колебания. Центральная частота 0 несущего колебания выбирается в за- |
||||
висимости от ряда технических и экономических факторов. Но в любомРслучае |
||||
|
|
|
У |
|
частота 0 должна быть велика по сравнению с наивысшей частотой спектра пе- |
||||
|
|
Г |
|
|
редаваемого сообщения и шириной спектра |
c |
самого несущего колебания. |
||
|
|
Б |
|
|
Это объясняется тем, что для неискаженной передачи сообщения через радиотехнические цепи, а также для устранения искажений, обусловленных распространением радиоволн, необходимо, чтобы ширина спектра радиосигнала Fs pb
(определяется шириной спектра сообщения Fi и шириной спектра несущего ко- |
||||||
|
|
|
|
к |
|
|
лебания Fc ) была мала по сравнению с |
f0 0 |
/ 2 ; чем меньше отношение |
||||
F |
|
|
|
е |
|
|
/ f |
0 |
, |
тем меньше проявляется несовершенство характеристик системы. |
|||
s pb |
|
|
|
а |
|
|
Поэтому чем выше требуемая скорость п р дачи информации, и, следовательно, шире спектр радиосигнала Fs pb , м выше должна быть несущая частота. Как
правило, выполняется неравенс во Fs pb / f0 1.
Любой радиосигнал м жно поэ ому трактовать как «узкополосный» про-
кажений передаваемых сообщений.
цесс даже при передаче «ш р к полосных» сообщений. |
||||||
|
|
|
|
|
|
т |
Основной пр |
п полосовой модуляции заключается в переносе инфор- |
|||||
|
|
|
|
|
о |
|
мационного сообщен я в несущий сигнал и последующей его передаче по физи- |
||||||
|
|
|
|
нци |
|
|
ческому кана у. По осовая демодуляция – это обратный процесс извлечения ин- |
||||||
формационного сообщения из принятого полосового (радиосигнала). |
||||||
|
|
|
л |
|
|
|
Искажения передаваемого радиосигнала в физическом канале могут приво- |
||||||
дить к ош |
|
в процессе демодуляции. Основная цель полосовой модуляции – |
||||
|
бкам |
|
|
|
||
передача |
|
нформационных сообщений с высокой скоростью и минимизацией ис- |
||||
и |
|
|
|
|
||
Б |
|
|
|
|
|
|
В общем случае модулированный радиосигнал может содержать информацию, закодированную в закон изменения амплитуды A(t) , частоты f (t) или фа-
зы (t) несущего колебания.
Таким образом, модулированный радиосигнал может быть представлен следующим образом:
s(t) A(t) cos 2 f0 f (t) t (t) 0 A(t) cos 2 fot (t) , (11.1)
153
где (t) 2 f (t)t (t) 0 – фазовый набег относительно гармонического несущего колебания cos 2 fot . Следует отметить, что законы изменения амплитуды, частоты и фазы A(t) , f (t) , (t) могут комбинировать в себе
как закон изменения соответствующих параметров под воздействием передаваемого сообщения, так и законы изменения данных параметров в квазигармоническом несущем колебании.
Разложив косинус суммы, можно представить радиосигнал как комбинацию синфазной и квадратурной компонент:
|
s(t) SI (t)cos 2 f0t SQ (t)sin 2 f0t , |
(11.2) |
||
где |
SI (t) A(t) cos (t) и SQ (t) A(t)sin (t) – синфазная и квадратурная |
|||
|
|
|
И |
|
компонента модулированного радиосигнала соответственно. Следует отме- |
||||
тить, что рассмотренные представления радиосигнала представляютРкомби- |
||||
нированную амплитудно-угловую модуляцию. |
У |
|
||
|
|
Г |
|
|
|
Выбор метода модуляции (метода наложения передаваемой информа- |
|||
ции на параметры несущего колебания) определяется различными требова- |
||||
|
|
|
|
Б |
ниями, предъявляемыми к радиосигналам. К данным требованиям относятся: |
||||
1. Спектральная эффективность – отношение скорости передачи ин- |
||||
формации к необходимой полосе |
|
, занимаемой радиосигналом |
||
|
|
|
частот |
|
[(бит/с)/Гц]. (Необходимая ширина полосы ч стот: ширина полосы частот, |
||||
|
|
к |
|
|
которая достаточна при данном классе излучения для обеспечения передачи |
||||
|
е |
|
|
|
сообщений с необходимой скоростью и |
чеством при определенных усло- |
|||
виях). |
т |
|
|
|
2. Помехоустойчивость – минимальное отношение мощности полезного сигнала к мощности помехи (шума), обеспечивающее демодуляцию с качеством не хуже заданного (для сис ем цифровой радиосвязи принято характеризовать минимальным ношением энергии приходящейся на один бит
передаваемой инф рмац и к спектральной плотности шума на входе демоду- |
||
лятора, обеспеч вающее вероятность ошибки, не более заданной). |
||
3. |
|
о |
Компактность спектральной плотности – характеризуется уровнем |
||
мощности, проникающейив соседний частотный канал. |
||
4. |
Постоянство огибающей – характеризуется глубиной амплитудной |
|
модуляц |
л |
|
радиосигнала и накладывает существенные ограничения на воз- |
||
можность спользования нелинейного усиления (например, усилителей, ра- |
|
|
б |
и |
|
Б |
|
ботающ х в режиме С) в радиотрактах с целью повышения их энергетической эффективности.
11.2. Краткий обзор методов цифровой (дискретной) модуляции
Краткая характеристика и принятые международные сокращения основных видов цифровой модуляции приведены в табл. 11.1.
154

Таблица 11.1
Основные методы цифровой модуляции
Аббревиатура |
|
Альтернативная |
|
Описание |
|
|
|||||
|
аббревиатура |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
||
1 |
|
|
|
2 |
|
|
|
3 |
|
|
|
|
|
Частотная манипуляция (Frequency Shift Keying) |
|
||||||||
|
|
|
|
|
|
|
Бинарная (двухпозиционная) частотная |
||||
BFSK |
|
|
|
FSK |
|
|
манипуляция |
(Binary |
Frequency Shift |
||
|
|
|
|
|
|
|
Keying) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Р |
MFSK |
|
|
|
|
|
|
М-позиционная частотная манипуляция |
||||
|
|
|
|
|
|
|
(M-ary Frequency Shift Keying) |
|
|||
|
|
|
|
Фазовая манипуляция (Phase Shift Keying) |
И |
||||||
|
|
|
|
|
|
||||||
BPSK |
|
|
|
PSK |
|
|
Бинарная (двухпозиционная) фазовая |
||||
|
|
|
|
|
манипуляция (Binary Phase Shift Keying) |
||||||
|
|
|
|
|
|
|
|||||
QPSK |
|
|
|
4PSK |
|
|
Квадратурная фазовая манипуляция |
||||
|
|
|
|
|
(Quadrature Phase Shift Keying) |
|
|||||
|
|
|
|
|
|
|
|
||||
OQPSK |
|
|
|
SQPSK |
|
|
Квадратурная |
фазовая |
манипуляция со |
||
|
|
|
|
|
|
У |
|
||||
|
|
|
|
|
|
|
сдвигом (Offset QPSK, Staggered QPSK) |
||||
|
|
|
|
|
|
|
Г |
||||
π/4-QPSK |
|
|
|
|
|
π/4-Квадратурная фазовая манипуляция |
|||||
|
|
|
|
|
(π/4-Quadrature Phase Shift Keying) |
||||||
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
Б |
||||
|
|
|
|
|
|
|
М-позиционн я фазовая манипуляция |
||||
MPSK |
|
|
|
|
|
|
к |
|
|
|
|
|
|
|
|
|
|
|
(M-ary Phase Shift Keying) |
|
|
||
|
|
а |
|||||||||
Модуляция c непрерывной фазой (Continuous Phase Modulations – CPM) |
|||||||||||
|
|
|
|
|
т |
Одноинде сная фазовая модуляция |
|||||
SHPM |
|
|
|
|
(Single-h (modulation index) Phase Modu- |
||||||
|
|
|
|
|
|
|
еlation) |
|
|
|
|
MHPM |
|
|
|
|
|
|
Многоиндексная фазовая модуляция |
||||
|
|
|
и |
|
|
(Multi-h Phase Modulation) |
|
|
|||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
FFSKо |
|
Минимальная манипуляция. Быстрая ча- |
|||||
MSK |
|
|
|
|
стотная манипуляция (Minimum Shift |
||||||
|
|
|
|
|
|
|
Keying. Fast FSK) |
|
|
|
|
|
б |
|
|
|
|
|
|
|
|
|
|
GMSK |
|
л |
|
|
Гауссовская минимальная манипуляция |
||||||
и |
|
|
(Gaussian Minimum Shift Keying) |
||||||||
Ампл тудная и амплитудно-фазовая модуляция (Amplitude and Amplitude- |
|||
Б |
|
Phase Modulations) |
|
|
|
||
ASK |
|
|
Амплитудная манипуляция |
|
|
(Amplitude Shift Keying) |
|
|
|
|
|
OOK |
ASK |
|
Амплитудная манипуляция с пассивной |
|
паузой (Binary On-Off Keying) |
||
|
|
|
|
|
|
|
М-позиционная амплитудная манипуля- |
MASK |
MAM |
|
ция (M-ary ASK, M-ary Amplitude Modu- |
|
|
|
lation) |
QAM |
|
|
Квадратурная амплитудная модуляция |
|
|
(Quadrature Amplitude Modulation) |
|
|
|
|
|
155

Для систематизации существующей классификации методов модуляции на рис. 11.1 приведена схема, позволяющая определить взаимосвязь тех или иных модуляционных схем, широко используемых в современных телекоммуникационных системах.
Методы цифровой модуляции
|
|
|
|
|
Методы, обеспечивающие |
|
|
|
|
|
|
|
Методы, реализующие |
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
постоянство огибающей |
|
|
|
|
|
|
|
амплитудные изменения |
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
сигнала |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
сигнала |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
FSK |
|
|
|
|
|
|
|
PSK |
|
|
|
|
|
|
|
|
|
|
CPM |
|
|
|
|
|
ASK |
|
|
QAM |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Р |
||
|
|
|
|
|
|
N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
OOK |
|
|
MASK |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
BPSK |
|
|
|
MPSK |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D |
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
N |
|
|
N |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
QPSK |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Г |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
π/4-QPSK |
|
|
OQPSK |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
BFSK |
|
|
|
|
MFSK |
|
|
|
|
|
|
|
|
|
|
MSK |
|
|
SHPM |
|
MHPM |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N |
|
|
|
|
|
N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
к |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
GMSK |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Рис. 11.1. Классификация методов цифровой модуляции |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Следует отметчтоть, |
некоторые из видов модуляции, в зависимости |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
от исходных предпосылок могут быть получены (классифицированы) больше |
||
|
б |
|
чем из одной «родительской» ветви (схемы). Кроме того, методы, где может |
||
иметь |
|
|
быть примененолдифференциальное (относительное) кодирование, отдельно |
||
марк рованы символом D, аналогично методы модуляции, которые могут |
||
Б |
|
|
обеспеч вать некогерентную демодуляцию, маркированы символом N. Сле- |
||
дует |
|
в виду, что принципы когерентной демодуляции применимы к |
любой модуляционной схеме.
Все виды модуляции можно разделить на две большие категории: методы модуляции, обеспечивающие постоянство огибающей радиосигнала, и методы модуляции, приводящие к амплитудным изменениям сигнала. В каждой из указанных категорий можно выделить базовые методы модуляции. Это FSK (частотная манипуляция), PSK (фазовая манипуляция) и CPM (непрерывная фазовая модуляция) для категории модуляционных схем, обеспечивающих постоянство огибающей радиосигнала и ASK (амплитудная мани-
156
пуляция) и QAM для категории модуляционных схем, приводящих к амплитудным изменениям сигнала.
Остальные модуляционные схемы являются производными от базовых и получаются на основе базовых методов путем их видоизменения, комбинации и наложения ограничений на параметры и характеристики.
Охарактеризуем кратко основные методы модуляции.
BFSK – бинарная (двухпозиционная) частотная манипуляция. Сигнал представляет собой непрерывное гармоническое колебание, закон изменения частоты которого представляет прямоугольное колебание в соответствии с
передаваемыми символами (один символ модуляции кодирует один бит пе- |
|
редаваемого цифрового потока). |
Р |
|
|
MFSK – М-позиционная частотная манипуляция. Сигнал представляет |
|
|
И |
непрерывное гармоническое колебание, закон изменения частоты которого |
|
представляет М-уровневый прямоугольный процесс в соответствии с переда- |
||
|
|
У |
ваемыми символами (один символ модуляции соответствует группе из не- |
||
скольких бит передаваемого цифрового потока). |
Г |
|
BPSK – бинарная фазовая манипуляция. Сигнал представляет непре- |
||
Б |
|
|
рывное гармоническое колебание с постоянной частотой, фаза которого может принимать одно из двух заданных значений в соответствии с передаваемыми символами (один символ модуляции кодирует один бит передаваемого цифрового потока).
QPSK – квадратурная фазовая м нипуляция. Сигнал представляет со-
бой непрерывное гармоническое |
ние с постоянной частотой, фаза ко- |
||
|
|
а |
|
торого может принимать одно из ч тыр х значений в соответствии с переда- |
|||
ваемыми символами (один символ модуляциик |
кодирует два бита передавае- |
||
мого цифрового потока). |
колеб |
|
|
|
|
|
|
OQPSK – квадратурная фазовая манипуляция. Разновидность QPSK, |
|||
исключающая одновременную смену символов в квадратурных составляю-
щих совокупного |
сигнала. |
|
|
|
т |
/4-QPSK – разн в дн сть QPSK, обеспечивающая сдвиг фазы между |
||
|
о |
|
сигналами, представ яющ ми различные символы, кратный /4. Может рас- |
||
сматриваться как комбинация двух сигналов с /2-BPSK квадратурных не- |
||
сущих коле аний.ради |
|
|
л |
|
|
M-PSK – М-позиционная фазовая манипуляция. Сигнал представляет |
||
непрерывноеибгармоническое колебание с постоянной частотой, фаза которого можетБпр н мать одно из М заданных значений в соответствии с передаваемыми символами (один символ модуляции кодирует несколько бит передаваемого цифрового потока).
SHPM – непрерывная фазовая модуляция с постоянным индексом модуляции. Модуляция осуществляется импульсами специальной формы без разрывов во временной области (сглаженных по тому или иному закону).
MHPM – непрерывная фазовая модуляция безразрывными импульсами специальной формы при которой индекс циклически принимает одно из М возможных значений.
157

MSK – минимальная манипуляция. Частотная манипуляция с минимальным сдвигом и непрерывной фазой. Под минимальным сдвигом понимается такое значение девиации частоты, при которой фазовый набег сигнала за длительность передаваемого символа составляет /2 относительно несущего колебания.
GMSK – разновидность MSK. Манипуляция осуществляется импульсами гауссовской формы.
ASK – амплитудная манипуляция. Сигнал представляет собой гармоническое колебание с постоянной частотой и фазой, закон изменения ампли-
туды которого определяется передаваемыми символами. |
Р |
|
|
OOK – разновидность амплитудной манипуляции. Особенность данно- |
|
го вида модуляции заключается в пассивной паузе при передаче одного из |
|
двух возможных передаваемых символов. |
И |
|
|
MASK – M-позиционная амплитудная манипуляция. зменение амплитуды радиосигнала осуществляется по одному из М возможных законов (со-
|
Г |
|
стояний). Один символ модуляции кодирует несколько бит передаваемого |
||
цифрового потока. |
Б |
|
QAM – квадратурная фазовая манипуляция. ПередаваемыеУ |
символы |
|
кодируются одним из нескольких возможных состояний амплитуды и
начальной фазы гармонического колебания с постоянной частотой. Один |
||
|
|
а |
символ модуляции кодирует несколько бит передаваемого цифрового потока. |
||
|
е |
|
11.3. Представление радиосигнала в комплексном виде. |
||
Аналитический сигнал |
к |
|
11.3.1. Комплексные числа |
|
|
измерениях. Они класс математических объектов, определяемый
Комплексныесоставляютчислат(иногда называемые мнимыми числами) не являются числами в элементарн м смысле слова, применяемыми при подсчетах и
описанными н же свойствами. |
|
|
|
|
||||
|
|
|
и |
|
|
можно поставить в соответствие |
||
|
|
|
|
|
|
|||
|
Каждому комплексному числу c |
|||||||
единственную пару a, b |
действительных чисел a и b и обратно. |
|||||||
|
|
л |
|
|
|
|
|
|
|
Каждое комплексное число |
|
в виде суммы |
|||||
|
c может быть записано |
|||||||
|
б |
|
|
|
|
|
jb , мнимая еди- |
|
|
|
|
|
|
|
|
||
c a jb действительного числа a и чисто мнимого числа |
||||||||
ницаиj определяется условием j |
2 |
1 . |
|
|
||||
|
Действительные числа a Re c и |
|||||||
|
|
|
|
|
|
|
|
|
b Im c соответственно называются действительной частью и мнимой ча- |
||||||||
Б |
|
|
|
|
|
|
|
|
стью комплексного числа c . Два комплексных числа c a jb и c* a jb, |
||||||||
имеющие одинаковые действительные и противоположные |
мнимые части, |
|||||||
называются сопряженными комплексными числами. Два комплексных числа равны в том и только том случае, если соответственно равны их действительные и мнимые части.
158
Любое действительное число можно представить точкой на действительной оси (это «одномерные» числа). Комплексное число тоже можно представить точкой, только на плоскости (см. рис. 11.2). Эту плоскость называют комплексной плоскостью, она дает нам возможность изображать комплексные числа, имеющие как действительную, так и мнимую части.
|
|
|
|
|
|
|
|
b |
|
|
|
Мнимая ось |
|
|
|
|
|
|
Комплексное число |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
arctg |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c a jb |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
a |
|
|
|
|
jb |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Р |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
φ |
|
|
|
|
|
|
|
|
|
|
|
И |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
a |
2 |
b |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
c |
|
|
|
|
|
|
cc * |
|
|
|
|
|
|
a |
Действительная ось |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
Рис. 11.2. Графическое представление комплексного числа |
|
|||||||||||||||||||||||||||
|
В соответствии с рис. 11.2 мы можем использоватьГ |
геометрические |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
числа |
|
|
|
|
|
|
|
|
|
|
|
|||
свойства прямоугольного треугольника для получения нескольких различных |
|||||||||||||||||||||||||||||||||
способов представления комплексного |
|
|
|
.Б |
|
|
|
|
|||||||||||||||||||||||||
|
|
c |
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
к |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Комплексное число c |
может быть з пис но несколькими различными |
|||||||||||||||||||||||||||||||
способами, показанными в табл. 11.2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Предс авлениеекомплексного числа |
Таблица 11.2 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Название |
|
т |
|
|
|
Математическое выражение |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a jb |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
|
|
||||||||||||
Алгебраическая (прям уг льная форма) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
о |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
Тригонометр ческая форма |
|
|
|
c |
|
c |
|
cos(υ) j sin(υ) |
||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Экспоненциа ьная (по ярная) форма |
|
|
c |
c |
e |
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
jυ |
|
|
|
|||||||||||||
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Модуль-аргумент |
|
|
|
|
|
|
c |
|
c |
υ |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
л |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Экспоненциальная форма записи непосредственно вытекает из тригонометрической на основании разложения в ряд функций cos( x ) и sin( x ) :
159

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
2n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
cos(x) 1 |
|
|
( 1)n |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
(2n)! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
2n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
sin(x) |
|
|
|
|
|
|
|
|
|
( 1)n 1 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(11.3) |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
n 1 |
|
(2n 1)! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
( jx) |
n |
|
|
|
|
|
|
|
|
|
|
x |
2n |
|
|
|
|
|
|
|
|
|
x |
2n 1 |
|
|
|
|
|||||||||||||||||||
|
|
|
e jx 1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
( 1)n j |
|
|
|
|
|
( 1)n 1 |
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
n! |
|
|
|
|
|
|
|
|
n 1 |
|
(2n)! |
|
|
|
|
|
|
n 1 |
|
(2n 1)! |
|
|
|||||||||||||||||||||||
|
|
|
cos(x) j sin(x) (формула Эйлера) |
|
|
|
|
|
|
|
|
|
Р |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Математические операции над комплексными числами подчиняются |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
|
тем же правилам, что и операции над действительными числами. |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
c1 a1 jb1; |
|
|
c2 a2 jb2 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
c1 c2 a1 a2 j(b1 b2 ); |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Г |
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
c c (a jb )(a jb ) a a j |
2b b j(a b |
|
a b ) |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
1 |
2 |
|
|
1 |
|
1 |
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|
1 |
2 |
1 |
2 |
|
|
2 |
1 |
|
|
|
|
||||||||||||
a a b b j(a b a b ) |
|
c |
|
|
|
|
c |
|
e j (υ1 υ2 ) ; |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
1 |
2 |
|
1 |
2 |
|
|
|
|
1 |
|
|
|
2 |
|
|
|
2 |
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
c1 |
|
c1c2* |
|
c1c2* |
|
|
|
|
e jυ1 |
|
c2 |
|
e jυ2 |
|
|
|
|
c1 |
|
|
e j (υ1 |
υ2 ) . |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
c1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
c2 |
|
|
|
c2c2* |
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c2 |
|
|
|
Б |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
11.3.2. Комплексное пр дставлкние радиосигнала |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Рассмотрим радиосигнал как комбинацию синфазной и квадратурной |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
компонент: |
|
|
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
л |
|
|
|
|
|
|
|
s(t) SI (t)cos 2 f0t SQ (t)sin 2 f0t , |
|
|
|
(11.4) |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
где |
S |
(t) |
A(t)cos |
(t) |
и |
|
|
S |
Q |
(t) A(t)sin (t) |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
I |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
– синфазнаяиквадратурная компонента модулированного радиосигна- |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
ла, соответственно. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Определим некоторую функцию S(t) через синфазную и квадратурную |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
составляющую следующим образом: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
S(t) SI ( t ) jSQ( t ).
Данная функция несет всю информацию об изменениях амплитуды, частоты и фазы модулированного радиосигнала.
Умножим определенную выше функцию на комплексную экспоненту
e j 0t :
160

S(t)e j 0t SI (t) jSQ (t) e j 0t |
SI (t) jSQ (t) cos( 0t) jsin( 0t) |
|
||||||||||
S |
(t)cos( t) S |
Q |
(t)sin( t) |
j S |
(t)sin( t) S |
Q |
(t)cos( t) . |
|
|
|||
I |
0 |
0 |
|
I |
|
0 |
|
0 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Действительная часть функции |
S(t)e j 0t полностью определяет моду- |
||||||||||
лированный радиосигнал |
|
|
|
|
|
|
|
|
|
|||
|
Re S(t)e j 0t SI (t)cos( 0t) SQ (t)sin( 0t), |
|
|
|
|
Р |
||||||
мнимая часть Im S(t)e j 0t |
SI (t)sin( 0t) SQ (t)cos( 0t) |
|
|
|||||||||
является сопряженным |
||||||||||||
по Гильберту отображением модулированного радиосигнала. |
И |
|||||||||||
|
|
|||||||||||
|
Преобразование Гильберта – это процедура, выполняемая над действи- |
|||||||||||
|
|
|
|
|
|
|
|
|
|
У |
|
|
тельным сигналом s( t ) и дающая новый действительный сигнал sht ( t ) (со-
пряженный по Гильберту). При этом sht ( t ) представляет собой сдвинутую
по фазе на 90° версию сигнала s( t ) . |
Б |
|
|
Отличие нового сигнала sht ( t ) от исходного наиболее заметно при |
|
анализе их Фурье-образов (преобразований Фурье). ГА именно: все компонен- |
|
|
равны |
ты sht ( t ) с положительными частотами |
компонентам s( t ) с положи- |
тельными частотами, сдвинутым по ф зе на минус 90°, а все компоненты
sht ( t ) с отрицательными частотами р вны |
омпонентам s( t ) с отрицатель- |
|||||||||||||
|
|
|
|
|
|
|
|
фазе |
|
|
|
|
||
ными частотами, сдвинутым по |
|
на +90°. |
|
|
|
|
||||||||
|
Комплексную |
|
нент |
к |
|
|
j 0t |
принято называть |
||||||
|
функцию |
вр м ни sa( t ) S(t)e |
|
|||||||||||
аналитическим сигналом, а функцию |
|
|
|
|
|
|||||||||
S(t) – комплексной огибающей радио- |
||||||||||||||
сигнала. |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Спектральные |
с бенн с и сопряженных по Гильберту сигналов обу- |
||||||||||||
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
словливают отсутств е к мп |
|
с отрицательными частотами в спектре |
||||||||||||
аналитического с гналао. Действительно, для области отрицательных частот |
||||||||||||||
выполняется соотношен е |
Sht ( j ) jS( j ), а для области положительных |
|||||||||||||
|
|
|
б |
|
|
|
Sht ( j ) и S( j ) – |
|
|
|
||||
частот |
Sht ( j ) jS( j ) , |
где |
комплексные спектраль- |
|||||||||||
ные |
функции |
л(спектры) сопряженного по Гильберту сигнала sht ( t ) и исход- |
||||||||||||
|
|
|
||||||||||||
ного с |
гнала s( t ) . Тогда спектр аналитического сигнала может быть записан |
|||||||||||||
Б |
|
|
|
|
|
|
|
|
|
|
|
|
||
следующ м образом: |
|
|
|
|
|
|
|
|
|
|||||
161
|
|
s( t ) jsht ( t ) e j t dt |
|
|
|||
Sa ( j ) sa ( t )e j t dt |
|
|
|
||||
|
|
|
|
|
|
||
|
S( j ) j( jS( j )); |
0 |
|
||||
S( j ) jSht ( j ) |
|
|
|
|
|
|
|
|
S( j ) j( jS( j )); |
0 |
|
||||
S( j ) S( j ); |
0 |
|
2S( j ); |
0; |
|
|
|
|
|
|
0. |
|
|
|
|
S( j ) S( j ); |
0 |
0; |
|
|
|
||
Таким образом, модулированный радиосигнал может быть представлен
экспоненциальную форму записи аналитического сигнала, несетРинформацию только о центральной частоте исходного радиосигнала (не включает в
комплексной функцией времени (аналитическим сигналом), сохраняющей
все особенности исходного сигнала. Поскольку множитель e j 0t , входящий в
себя законы информационной модуляции и особенности формы несущего
колебания), то при решении широкого круга задач формирования и обработ- |
|||||||||||
|
|
|
|
|
|
|
|
|
|
И |
|
ки модулированных радиосигналов достаточно рассмотрения только ком- |
|||||||||||
плексной огибающей |
|
|
|
|
|
|
реального |
||||
S(t) , включающей в себя все особенностиУ |
|||||||||||
сигнала. |
|
|
|
|
|
|
|
Г |
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
11.3.3. Замечания по поводу отриц тельных частот |
|
|||||||||
|
|
|
|
|
|
|
|
а |
|
|
|
|
Понятие отрицательной частоты служит состоятельным и мощным ин- |
||||||||||
струментом при анализе и |
|
к |
|
|
|
||||||
|
сигналов. Использование отрицательной |
||||||||||
|
|
|
|
|
|
зе |
|
|
|
|
|
|
|
|
|
|
синт |
|
|
|
|
|
|
частоты становится обяза ельным при представлении действительных сигна- |
|||||||||||
лов в комплексной записи. |
|
|
|
|
|
|
|||||
|
Трудности п нимания идеи о рицательной частоты сродни тому оце- |
||||||||||
пенению, которое |
щущал сь в среде средневековых математиков, когда они |
||||||||||
впервые |
|
|
|
с отрицательными числами. Вплоть до тринадцатого |
|||||||
|
|
|
|
о |
|
|
|
|
|
|
|
века отрицате ьные ч сла рассматривались как фиктивные, потому что числа |
|||||||||||
обычно испо ьзоваись для счета и измерения. Соответственно, отрицатель- |
|||||||||||
|
|
столкнул |
|
|
|
|
|
|
|
|
|
ные |
|
просто не имели смысла (как может существовать нечто, которое |
|||||||||
числа |
|
|
|
|
|
|
|
|
|
||
меньше, чем ничто?). Идея вычитания шести из четырех должна была казать- |
|||||||||||
Б |
|
|
|
|
|
|
|
|
|
|
|
ся бессмысленнойб |
. Историки математики предполагают, что отрицательные |
||||||||||
числа впервые были введены в оборот в Италии. Как свидетельствует история, около 1200 г. итальянский математик Фибоначчи работал над некой финансовой проблемой, единственное допустимое решение которой включало отрицательные числа. Отважный Лео писал: «В отношении этой проблемы я показал, что она неразрешима, если только не допустить, что первый человек имел долг».
Современное понимание отрицательных чисел связано с направлением. назад от нуля в том смысле, что положительные числа показывают направление вперед от нуля. Таким образом, понятие отрицательного числа вполне
162
состоятельно, если мы определяем его соответствующим образом. Как бы ни были для нас привычны отрицательные числа, отрицательная частота остается трудным и сомнительным понятием для многих.
Отрицательная частота представляет собой вполне состоятельное понятие, если мы правильно определяем ее по отношению к тому, что мы называем положительной частотой.
Как нам уже известно, гармоническое колебание с круговой частотой0 в комплексном виде может быть представлено функцией следующего ви-
да – e j 0t . Геометрическая интерпретация данной функции представляет со-
бой вращающуюся по единичной окружности в направлении против часовой
смотрим поведение комплексной экспоненты в случае отрицательногоРзначения круговой частоты. В этом случае направление вращения точки, пред-
стрелки точку на комплексной плоскости (см. рис. 11.3). Проекция данной
точки на действительную ось является функцией сигнала – cos( 0t) . ас-
ставляющей комплексную экспоненту, изменится на противоположноеИ . При этом проекция точки на действительную ось не изменится и останется преж-
ней ( cos( |
|
0 |
|
t) ), изменению подвергнется только проекция точки на мнимую |
||||||||||||||||
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
|
ось ( sin( 0t) , для 0 сменится на sin( |
|
0 |
|
|
|
|||||||||||||||
|
t) , для 0 ). |
|||||||||||||||||||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Г |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
||
|
|
|
|
|
|
|
|
|
jy |
|
|
|
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
j 0t |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
е |
к |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
0 0 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
т |
|
|
|
|
|
|
1 |
|
х |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
л |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
б |
Рис. 11.3. Интерпретация отрицательной частоты |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
иПоскольку физически реализуемым сигналом является проекция ком- |
||||||||||||||||||||
плекснойБ экспоненты на действительную ось, то смысл в отрицательной частоте отсутствует (так же, как отсутствовал смысл отрицательных чисел для средневековых математиков). Но это применимо только для нулевой точки
отсчета. Рассмотрим линейную комбинацию колебаний e j 0t e j 0t . Данное колебание есть не что иное, как 2cos( 0t) . Осуществим линейное изменение
системы координат в виде сдвига точки отсчета частоты на значение , в результате этого получим
163
|
e j 0t e j 0t |
|
e j t |
e j ( 0 )t e j ( 0 )t |
|
|
|
|
11.5 |
|
Действительная часть полученной комплексной функции соответствует физическому колебанию, подчиняющемуся следующему закону:
Re e j 0t e j 0t e j t Re e j ( 0 )t e j ( 0 )t
Re cos 0 t jsin 0 |
|
t |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Re cos 0 |
t jsin 0 |
t |
|
|
|
(11.6) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Р |
||
cos t |
cos |
|
|
|
t . |
|
|
|
|||||||
|
|
|
|
|
|||||||||||
|
0 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Как можно заметить, «абсолютно» эквивалентные в нулевой точке от- |
|||||||||||||||
счета колебания e |
j 0t |
и |
e |
j 0t |
|
|
|
|
|
|
И |
||||
|
|
|
|
совершенно не эквивалентны и дают совер- |
|||||||||||
шенно разный результат, если пронаблюдать их «со стороны». |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
|
|
Таким образом, отрицательное значение частоты можно определить как |
|||||||||||||||
направление вращения вектора сигнала. |
|
Г |
|
|
|||||||||||
|
|
|
|
|
|||||||||||
Понятие отрицательной частоты является крайне важным в теории сиг- |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
налов, поскольку его использование позволяет осуществлять синтез сигналов |
|||||||||||||||
с повышенной спектральной эффе тивностьюа, также является основополагающим при так называемой квадратурной обработке сигналов.
Мы определили отрицат льную частоту в частотной области. Если |
|||||||
коллеги хотят заявить, что |
к |
||||||
|
льная частота не существует во времен- |
||||||
ной области, мы не будем спориеь. Однако наше определение отрицательной |
|||||||
частоты в частотной |
|
блас и являе ся однозначным, совместимым с действи- |
|||||
тельными сигналами |
|
чень полезным, и мы будем его придерживаться. |
|||||
|
|
|
|
отрицат |
|
|
|
|
|
о |
|
|
|
||
11.3.4. Зак юч тельные замечания |
|||||||
|
и |
|
|
|
|
||
Может возникнуть вопрос: зачем необходимо комплексное (более |
|||||||
|
л |
|
|
|
|
|
|
«сложное») представление сигналов? Чтобы ответить на данный вопрос, еще |
|||||||
раз обратбм внимание на некоторые особенности, присущие комплексному |
|||||||
представлен ю модулированных радиосигналов. |
|||||||
и |
|
|
|
|
|
|
|
1. Составной частью комплексного описания (аналитического сигнала) |
|||||||
является комплексная экспонента e |
j 0 |
, которая несет информацию только о |
|||||
Б |
|
|
|
|
|
|
|
центральной частоте модулированного радиосигнала.
2. Вся информация о законах модуляции содержится непосредственно
в комплексной огибающей аналитического сигнала S(t).
3. Поскольку спектр (образ Фурье) аналитического сигнала sa ( t ) не содержит компонент с отрицательными частотами и повторяет физический
164
спектр реального радиосигнала s( t ) , то спектр комплексной огибающей S(t) полностью копирует спектр модулированного радиосигнала s( t ) при условии перемещения его центральной частоты в нуль.
4. Спектр комплексной огибающей S(t) содержит как компоненты с
отрицательными, так и компоненты с положительными частотами. При этом отрицательная область частот необязательно является симметричной копией положительной области частот относительно ноля (область отрицательных частот становится информативной, а не просто «формальной»).
Указанные особенности аналитического сигнала и комплексной огиба-
сигнала с последующим формированием комплексной огибающейИРметодами преобразования Фурье и переносом ее на рабочую частоту квадратурным преобразователем частоты, что позволяет исключать информационное дуб-
ющей позволяют:
осуществлять непосредственный синтез спектра итогового радио-
лирование прилегающих снизу и сверху к центральной частоте полос частот модулированного радиосигнала;
|
осуществлять основную обработку радиосигналов (включая демо- |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
У |
дуляцию) в области нулевой частоты путем получения комплексной огиба- |
||||||||||||
ющей методами квадратурного преобразования частотыГ; |
||||||||||||
|
широко использовать цифровые методы, реализуемые специализи- |
|||||||||||
рованными процессорами, в задачах синтеза, |
Б |
|
||||||||||
н лиза и обработки радиосиг- |
||||||||||||
налов; |
|
|
|
|
|
|
|
|
|
|
|
|
|
повысить «информационную» эффективностьа |
дискретных преобра- |
||||||||||
|
|
|
|
|
|
|
|
|
|
к |
|
|
зований Фурье (количество информативных спектральных отсчетов увеличи- |
||||||||||||
вается в два раза). |
|
|
|
|
тать |
|
|
|
||||
|
Таким образом, комплексноееописание радиосигналов позволяет суще- |
|||||||||||
|
|
|
|
|
|
о |
|
|
|
|
||
ственно упростить ф рмир вание и обработку сигналов с использованием |
||||||||||||
|
|
|
онными |
|
|
|
|
|
||||
цифровых методов, разраб |
|
унифицированные алгоритмы модуляции и |
||||||||||
демодуляции сигнал в, |
существлять более «гибкое» управление спектраль- |
|||||||||||
|
|
л |
|
|
|
|
|
|
|
|||
ными, корреляц |
|
|
|
|
|
другими характеристиками формируемого сигна- |
||||||
ла. |
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11.4. Прямой и обратный переход между радиосигналом |
|||||||||||
Б |
|
|
|
|
|
|
|
|
|
|
|
|
|
егобкомплексным представлением |
|
|
|||||||||
|
Рассмотрим радиосигнал как комбинацию синфазной и квадратурной |
|||||||||||
компонент (11.4). |
|
|
|
|
|
|
|
|
|
|||
|
Комплексное представление такого сигнала (аналитический сигнал) |
|||||||||||
определяется следующим образом: |
|
|
|
|||||||||
|
|
|
S |
|
( t ) jS |
( t ) e |
j t |
s( t ) js |
( t ) . |
(11.7) |
||
|
s( t ) |
I |
0 |
|||||||||
|
|
|
|
|
|
Q |
|
|
|
ht |
|
|
165
где sht ( t ) – рассмотренный ранее сигнал, сопряженный по Гильберту с исходным сигналом s( t ) .
Таким образом, для получения комплексного представления радиосигнала достаточно иметь преобразователь Гильберта, формирующий мнимую составляющую аналитического сигнала. По сути, преобразователь Гильберта является широкополосным фазовращателем, обеспечивающим сдвиг каждой частотной компоненты исходного сигнала на 90°. Физическая реализация подобного фазовращателя затруднена, поэтому для получения действительной и мнимой составляющих аналитического сигнала, сдвинутых в частотной области относительно исходного сигнала, используют квадратурные преобразователи частоты. При этом сдвиг в частотной области обычно осуществляется в область нулевой частоты, что существенно облегчает дальнейшие опе-
рации над полученным комплексным представлением сигнала. Структурная |
|||||||||||||||
схема квадратурного преобразователя частоты представлена |
наРрис. 11.4. |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
|
|
Возможная ошибка установки частоты квадратурных опорных колебаний |
|||||||||||||||
учтена фазовым набегом ( t ) . |
|
|
Г |
И |
|||||||||||
|
|
|
|
|
|||||||||||
В результате операции квадратурного преобразования частоты имеем |
|||||||||||||||
|
x(t) SI (t)cos 0t SQ (t)sin 0t cos( 0t υ(t)) |
|
|
||||||||||||
|
SI (t)cos υ(t) |
SQ |
(t)sin υ(t) ; |
Б |
|
, |
(11.8) |
||||||||
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
к |
|
|
|
|
|
|
|
y(t) SI (t) cos 0t SQ (t) sin 0t sin( 0t υ(t)) |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
(11.9) |
|
|
SI (t) sin υ(t) SQ (t) cos υ(t) . |
|
|
|
|
|
|
||||||||
Для сравнения рассмо римеоперацию сдвига в область нулевых частот |
|||||||||||||||
|
|
|
|
о |
|
|
|
|
|
|
|
||||
аналитического сигнала: |
|
|
|
|
|
|
|
|
|||||||
|
|
|
и |
j (т0t (t )) |
|
|
|
|
|
|
|||||
SI (t) jSQ |
(t) e |
j 0t |
e |
(t) e |
j (t ) |
|
|
|
|
||||||
|
|
|
SI (t) jSQ |
|
|
|
|
||||||||
|
|
л |
|
|
|
|
|
|
|
|
|
|
|
|
|
SI (t) jSQ (t) cos(υ(t)) j sin(υ(t)) |
|
|
|
|
|
(11.10) |
|||||||||
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
SI (t) cos(υ(t)) SQ (t) sin(υ(t)) j SI (t) sin(υ(t)) SQ (t) cos(υ(t)) . |
|||||||||||||||
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
166

|
|
Х |
|
ФНЧ |
|
x(t) |
||
|
|
|
|
|
|
|
|
|
s(t) |
|
|
|
cos( 0t+ (t)) |
||||
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
||
|
|
|
Х |
|
|
|
|
ФНЧ |
|
|
y(t) |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
Р |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-sin( 0t+И(t)) |
|||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
У |
|
Рис. 11.4. Квадратурный преобразователь частоты |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
Г |
|
||
Сопоставляя полученные выражения, можно сделать вывод, что квад- |
|||||||||||||
ратурный преобразователь формирует |
|
своем выходе действительную и |
|||||||||||
|
|
|
|
|
|
|
|
|
Б |
|
|
||
мнимую компоненты комплексной огиб ющей исходного аналитического |
|||||||||||||
сигнала (его комплексного представления): |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
на |
|
|
||||
SI ( t ) jSQ( t ) e |
j ( t ) |
|
|
к |
|
|
|
|
(11.11) |
||||
|
|
x( t ) jy( t ). |
|
|
|
|
|
||||||
|
|
|
|
е |
|
|
|
|
|
|
|||
При этом наличие фаз вой ошибки при преобразовании частоты при- |
|||||||||||||
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|||
водит к фазовому запаздыванию полученного комплексного представления |
|||||||||||||
исходного радиос гнала на величину данной ошибки. Данное обстоятель- |
|||||||||||||
ство, как правило, требует принятия дополнительных мер по синхронизации
(компенсации ош |
) опорных колебаний квадратурного преобразователя |
бки |
|
частоты с несущим ко ебанием радиосигнала с точностью до фазы ( t ) 0 . |
|
Вопросы фазовойлсинхронизации при демодуляции будут рассмотрены поз- |
|
же. Следуетибзаметить, что при осуществлении квадратурного преобразования частотыБобязательным условием является опережение опорным колебанием в канале, формирующем действительную компоненту аналитического сигнала, опорного колебания в канале, формирующем мнимую компоненту аналитического сигнала, на фазовый угол, равный / 2 .
Обратное преобразование аналитического сигнала осуществляется квадратурным модулятором (рис. 11.5), реализующим перенос комплексной огибающей из области нулевой частоты в область рабочей частоты 0 .
Принцип формирования радиосигнала с заданной комплексной огибающей поясняется следующим соотношением:
167

Re SI (t) jSQ (t) e j 0t SI (t)cos 2 f0t SQ (t) sin 2 f0t s(t) . (11.12)
По аналогии с квадратурным преобразованием частоты принципиальным моментом при формировании радиосигнала является опережение опорным колебанием в синфазном канале ( I ) опорного колебания в квадратурном канале (Q ) на фазовый угол, равный / 2 .
|
SI ( t ) |
|
Х |
|
|
|
|
|
ПФ |
|
|
|
|
|
|
|
|
Р |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos( 0t+ (t)) |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
s(t) |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
|
|
||
|
SQ ( t ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
Г |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Х |
|
|
|
|
|
ПФ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
–sin( 0t+ (t)) |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
к |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
Рис. 11.5. Квадратурный модулятор |
|
|
|
|
|||||||||||||
11.5. Квазиоптимальн е принятие решений при приеме сигналов |
|
|||||||||||||||||||
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
с дискретной м дуляцией |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
11.5.1. Общая методология синтеза решающих правил при квази- |
|
|||||||||||||||||||
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
оптима ьном приеме сигналов с дискретной модуляцией |
|
|||||||||||||||||||
|
л |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Предположим, что сигнал зависит от нескольких параметров, часть из |
||||||||||||||||||||
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
которых подлежит определению, т.е. одни являются существенными, а |
||||||||||||||||||||
остальныеинесущественны. |
|
К первым относятся параметры 1,..., k |
, |
|||||||||||||||||
Б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
возможные значения которых известны и образуют область L . Ко вторым относятся параметры 1,..., l , возможные значения которых образуют
область F . Сигнал может быть записан в виде s( t, , ).
Сигнал s( t ) комбинируется с шумом n( t ) , образуя случайный процесс x( t ) . Процесс x( t ) наблюдается в моменты времени t1,...,tn . Выборочные значения X x1,...,xn образуют пространство входов решающего устройства .
168

Предполагаются известными статистика шума n( t ) и статистика пара-
метров и . По наблюдаемой выборке X x1,...,xn необходимо решить, какие значения имеют параметры 1,..., k .
Решающее устройство формирует на выходе решения D d1,...,dk ,
образующие область возможных решений G .
Будем считать, что когда принимается решение D , а параметры сигнала имеют значение , решающее устройство терпит ущерб, величина которого описывается заданной функцией потери W( D, ).
Введем решающую функцию (решающее правило) ( D X ) как услов-
ную плотность распределения вероятности случайной величины D при условии, что наблюдаются выборочные данные X . Обычно используется ва-
риант неслучайной решающей функции следующего вида |
|
Р |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(D |
|
X ) D * ( X ) |
d * ( X ) |
d |
|
* ( X ) ... |
|
И |
|||||||||||||||
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|
2 |
2 |
|
|
||||||
|
|
|
|
|
|
|
|||||||||||||||||
... d |
k |
* ( X ) |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
|
||||
* *1 ,..., *k . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Г |
|
|
|||||||||
|
|
|
|
|
|
|
* |
|
|
|
|
* |
|
|
|
|
Б |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Компоненты 1( x1,...,xn ) ,…, k ( x1 ,...,xn ) |
называют обычно оценками |
||||||||||||||||||||||
параметров 1,..., k . |
|
|
|
явля тсятакназываемый средний риск, ко- |
|||||||||||||||||||
Мерой качества оценки |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
к |
|
|
|
|
|
|
|
||||
торый определяется следующим образом. |
|
|
|
|
|
|
|
|
|
||||||||||||||
Образуется условная пло нос ь в роятности случайной величины D |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
|
|||
при условии, что параме ры сигнала имеют значение : |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
P( D |
|
) ( D |
|
X )P( X |
|
)dX , |
|
|
(11.13) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
где P( X |
|
) – функцияиправдоподобия вектора параметров (многомерная |
|||||||||||||||||||||
|
|||||||||||||||||||||||
плотность распределения вероятности выборочных значений x1,...,xn наблю- |
|||||||
|
|
л |
|
|
|
1,..., k |
|
даемого процесса x( t ) |
при условии конкретных значений |
вектора |
|||||
|
б |
|
|
|
|
|
|
параметров ). |
|
|
|
|
|
||
Совместная плотность распределения вероятности векторов D и за- |
|||||||
и |
|
|
|
|
|
|
|
писывается следующим образом: |
|
|
|||||
Б |
|
|
P( D, ) P( D |
|
)P( ), |
|
|
|
|
|
|
|
(11.14) |
||
|
|
|
|
|
|
|
|
где P( ) Pap ( ) – априорная (известная статистика параметров ) плот-
ность распределения вектора параметров .
Средний риск, по определению, равен средним потерям, присущим выбранному решающему правилу, т.е.
169
R dDd W( D, )P( D, )
G L |
|
||||
dXdDd W( D, ) ( D |
|
X )P( X |
|
)Pap( ) . |
(11.15) |
|
|
||||
|
|||||
G L |
|
|
|
|
|
Задавая различные функции потери, можно получать различные правила построения оценок параметров сигнала. Однако, какой бы вид не имели эти правила, все они будут основаны на операциях с апостериорной вероят-
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
ностью Pac( ) kP( X |
)Pap ( ) вектора параметров |
. При этом функция |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Р |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
правдоподобия существенных параметров P( X |
) получается усреднением |
|||||||||||||||||||||||||||||
по несущественным параметрам |
|
|
|
|
|
|
|
|
|
|
|
|
И |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
У |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
P( X |
|
) P( X |
|
, )Pap ( )d , |
|
(11.16) |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F |
|
|
|
|
|
|
|
|
|
Г |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
X при условии за- |
||||
где P( X , ) – плотность распределения вероятности |
||||||||||||||||||||||||||||||
данных конкретных значений и ; |
Pap ( ) – априорная плотность рас- |
|||||||||||||||||||||||||||||
пределения вероятности вектора . |
а |
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
Применительно к решению з д чи кв зиоптимальной демодуляции |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
к |
|
|
|
|
|
|
|
||||||
сигналов с дискретной модуляцией н иболее подходящей является простая |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
|
|
|
||||
функция потерь, имеющая следующий вид: |
|
|
|
|
|
|
|
|||||||||||||||||||||||
W( D, ) 1 ( D ) 1 ( d1 1 ) ( d2 2 )... ( dk k ) . |
(11.17) |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Минимизируем средний риск для простой функции потери: |
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
R |
1 |
dX dDт( D |
X )P( X |
D )Pap( D ) |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
G |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
1 |
|
|
dX |
|
dD D * ( X ) P( X |
|
D )P ( D ) |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ap |
|
|
|
* |
* |
|||||
и |
|
|
|
|
G |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
* |
|
|
|||
1 |
|
|
dX P( X |
|
* )P |
|
( * ) . |
|
|
|
|
|
|
|
|
|
(11.18) |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
л |
|
|
|
|
|
|
|
ap |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
)Pap( ) , |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
М н мум среднего риска соответствует максимуму P( X |
||||||||||||||||||||||||||||||
который достигается, |
если в качестве вектора оценок (в общем случае |
|||||||||||||||||||||||||||||
* ( X ) ) выбирать то значение, |
которое при любом значении X максимизи- |
|||||||||||||||||||||||||||||
рует апостериорную вероятность Pac( ). |
|
|
|
|
|
|
|
|||||||||||||||||||||||
В соответствии с вышеизложенным средний риск для простой функции потери минимизируется следующим правилом построения оценки парамет-
ров : в качестве оценок *1( x1 ,...,xn ) ,…, *k ( x1 ,...,xn ) выбирают значения,
170

обращающие |
в |
|
максимум |
апостериорную |
вероятность |
Pac ( 1 ,..., k ) kP( X |
|
1 ,..., k )Pap ( 1 ,..., k ). |
|
||
|
|
||||
В случае, если априорная вероятность вектора параметров постоянна на интервале существенного изменения функции правдоподобия, максимум апостериорной вероятности соответствует максимуму функции правдоподо-
бия P( X 1,..., k ) .
Оценки по максимуму правдоподобия находятся как решение системы уравнений правдоподобия:
|
|
ln P( X |
|
,..., |
k |
|
) 0 , |
|
|
|
Р |
|||||||
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|||||||||||||
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
ln P( X |
|
,..., |
k |
|
) 0. |
|
|
|
|||||||
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
||||||||||||
|
k |
|
|
1 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
В выражении для среднего риска |
|
|
И |
|||||||||||||||
|
|
|
|
|
|
|
R 1 |
|
|
dX |
|
dD ( D X )P( X D )P |
У |
(11.19) |
||||
|
|
|
|
|
|
|
|
|
( D ) |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
apГ |
|
|
||||
G
|
|
|
Б |
|
|
а |
|
интеграл в правой части представляет среднюю по априорной вероятности |
|||
|
к |
|
|
вероятность правильного решения. Миним льный средний риск при этом ра- |
|||
|
средней |
|
|
вен минимально возможной |
вероятности неправильного решения |
||
(вероятности ошибки). |
|
|
|
Необходимо отметить, |
получ нные правила построения оценок су- |
||
щественных параметров сигнала могут быть записаны и для случая непре-
|
|
|
о |
рывного наблюдения пу ем осущес вления соответствующих предельных |
|||
переходов. |
|
что |
|
|
л |
|
|
11.5.2. Синтез функции правдоподобия для канала связи |
|||
|
б |
|
|
с аддитивнымибелым гауссовским шумом |
|||
и |
|
|
|
11.5.2.1. |
Белый гауссовский шум |
||
Б |
|
|
|
Рассмотрим стационарный случайный процесс n( t ) , функция автокорреляции
которого равна дельта-функции, умноженной на некоторую постоянную величину
N0 / 2 :
R ( ) |
N0 |
( ) . |
(11.20) |
n |
2 |
|
Как известно, дельта-функция равна нулю всюду, за исключением точки0, где ( 0 ) , причем интеграл от дельта-функции по любому интервалу,
содержащему особую точку 0, равен единице.
171
Отсюда следует, что рассматриваемый случайный процесс характеризуется тем, что значения n( t ) в любые два сколь угодно близкие моменты времени не-
коррелированы. Поэтому такой процесс n( t ) можно назвать абсолютно случайным
процессом.
Спектральная плотность (распределение мощности по полосе частот) абсолютно случайного процесса определяется на основании теоремы Винера– Хинчина следующим образом:
|
|
|
j |
|
N0 |
|
|
|
j |
|
N0 |
|
|
j |
|
||||
|
Sn ( ) Rn ( )e |
|
d |
|
( )e |
|
d |
|
( |
)e |
|
d |
|
||||||
|
|
2 |
|
2 |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
N0 |
e j 0 |
|
N0 |
. |
|
|
|
|
|
|
|
|
(11.21) |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
Р |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Таким образом, спектральная плотность абсолютно случайного процесса |
||||||||||||||||||
постоянна при всех частотах. |
|
|
|
|
|
|
|
|
|
|
И |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Случайный процесс n( t ) , обладающий равномерным спектром в очень ши- |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
|
|
||
роком диапазоне частот, является «белым шумом» по аналогии с белым светом, |
|||||||||||||||||||
имеющим в видимой части равномерный сплошной спектр. |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Г |
|
|
|
|
||
|
Для белого шума формула спектральной плотности дает физически непонят- |
||||||||||||||||||
ный |
результат: |
дисперсия |
(средняя |
|
мощность) |
|
такого шума |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
||
n2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Sn( )d . Этот результат объясняется тем, |
что белый шум следует |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
|
|||
рассматривать как идеализацию, |
|
|
как реальные процессы всегда имеют |
||||||||||||||||
|
|
|
|
|
|
|
так |
|
|
|
|
|
|
|
|
||||
энергетический спектр, убывающий с частотой, и, следовательно, ограничен- |
|||||||||||
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
|
т |
|
|
|
|
|
||
ной средней мощностью. Белый шум является полезной математической иде- |
|||||||||||
|
|
|
о |
|
|
|
|
|
|
||
ализацией, |
применим й в |
|
ех случаях, когда время корреляции шума много |
||||||||
|
|
ли |
|
|
|
|
|
|
|
|
|
меньше всех существенных постоянных времени системы, на которую воз- |
|||||||||||
действует шум, |
, наче, к гда в пределах амплитудно-частотной характе- |
||||||||||
|
л |
|
|
|
|
|
|
|
|
|
|
ристики системы спектральную плотность воздействующего реального шума |
|||||||||||
можно |
иженно считать постоянной. |
|
|
|
|
|
|||||
Укажем, что ес и белый шум n( t ) представляет случайное напряжение, |
|||||||||||
и |
|
|
|
|
|
|
|
|
|
|
|
то вел ч на N0 |
имеет размерность N0 в |
2 |
/Гц |
в |
2 |
с . |
|||||
|
|
||||||||||
Б |
|
|
|
|
|
|
|
|
|
|
|
Определимприб многомерную плотность распределения вероятности белого |
|||||||||||
гауссовского шума на интервале времени 0,T . Для этого определим выбо- |
|||||||||||
рочные значения белого шума в момент времени ti |
следующим образом: |
||||||||||
|
|
|
ni |
1 |
ti t / 2 |
|
|
|
|
|
|
|
|
|
|
n( t )dt , |
|
|
|
|
(11.22) |
||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
t ti t / 2 |
|
|
|
|
|
|
где t – интервал дискретизации во времени. При этом реализация непрерывного случайного процесса на интервале времени 0,T представляется
172

набором выборочных значений n0 ,...,nM определенных для моментов времени t0 0,...,tk k t,...,tM M t T . Определим элементы автокорреляционной матрицы вектора выборочных значений n0 ,...,nM :
|
|
|
|
|
|
|
|
|
|
|
|
1 |
ti t / 2 |
|
|
|
|
1 |
|
ti t / 2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
nin j |
|
|
|
|
|
n( x )dx |
|
|
|
|
|
|
n( y )dy |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t ti t / 2 |
|
|
|
|
t ti t / 2 |
|
|
|
|
|
|
|
|
(11.23) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ti t / 2 ti t / 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n( x )n( y )dxdy . |
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
( |
t )2 ti t / 2 t j t / 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
где . |
– операция усреднения по ансамблю реализаций. Ввиду линейности |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
|
|
операций усреднения и интегрирования по времени очередность данных опе- |
||||||||||||||||||||||||||||||||||||||||||||
раций может быть изменена, тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
Г |
|
Р |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
ti t / 2 ti t / 2 |
|
|
|
|
|
|
У |
|
|
|||||||||||||||||
|
|
|
|
ni n j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n(x)n( y) dxdy . |
|
(11.24) |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
( t)2 t t / 2 t |
j |
t / 2 |
|
|
|
Б |
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n( x )n( y ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
Заметим, |
что |
|
|
|
по |
|
определению |
есть |
автокорреляционная |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
к |
|
|
|
|
|
|
|
|
|
|||||||||||
функция случайного процесса n( t ) : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
n( x )n( y ) R ( x y ) |
N0 |
( x y ) . |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
оN |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
С учетом этого перепишем выражение для элементов автокорреляци- |
|||||||||||||||||||||||||||||||||||||||||||
онной матрицы выб р чных значений n0 ,...,nM : |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
л |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
ti |
t / 2 ti |
t / 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
ni n j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
( x y )dxdy |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
( t )2 |
|
t |
tи/ 2 t t / 2 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
и |
|
|
i |
|
|
|
|
|
|
|
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
1 |
|
|
ti |
t /2 |
|
N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
N |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
0 |
|
dx; |
i j |
|
|
|
|
|
|
|
0 |
|
t; |
i |
j |
|
0 |
|
i j; |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|||||||||||||||||
|
|
( t) |
2 |
|
|
|
|
|
|
|
|
( t) |
2 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
ti t / 2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 t |
|
K |
(11.25) |
|||||||||||||
Б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
||||
|
|
|
0; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i j |
|
0; |
|
|
|
|
|
|
|
|
|
i |
j |
|
0; |
|
|
i j. |
|
||||||
|
Автокорреляционная матрица выборочных значений n |
,...,n содержит |
||||||||||||||||||||||||||||||||||||||||||
ненулевые элементы, расположенные только на главной диагонали. Это позволяет сделать заключение о взаимной некоррелированности выборочных значений n0 ,...,nM .
Пусть мгновенные значения исходного случайного процесса n( t ) подчиняются гауссовскому (нормальному) закону распределения вероятности,
173

тогда ввиду линейности операции дискретизации по времени выборочные значения n0 ,...,nM также будут распределены в соответствии с нормальной плотностью распределения вероятности.
|
1 |
|
( n )2 |
|
|
W( ni ) |
|
exp |
i |
, |
|
2 n |
2 n2 |
||||
|
|
|
где 2 |
n2 |
|
N0 |
– диагональный элемент автокорреляционной матрицы |
||
|
||||||
n |
i |
|
2 t |
|
Р |
|
|
|
|
|
|||
выборочных значений шума. |
||||||
|
||||||
В случае гауссовских случайных величин некоррелированность авто- |
||||||
|
|
|
|
|
И |
|
матически предполагает независимость, на основании этого многомерная |
||||||
плотность распределения вероятности совокупности выборочных значений |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
У |
|
|
|||
записывается следующим образом: |
|
|
|
Г |
|
|
|
|||||||||
|
|
|
|
|
|
M 1 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
||
|
|
M |
) |
|
1 |
exp |
|
|
1 |
|
M |
|
. |
|
||
W ( n ,...,n |
) W ( n |
|
|
|
|
|
|
n2 t |
(11.26) |
|||||||
0 |
M |
i |
|
|
N0 |
|
|
|
N0 i 0 |
i |
|
|
||||
|
|
i 0 |
|
|
|
|
|
|
||||||||
|
|
|
|
2 |
а |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
2 t |
|
|
|
|
|
|
|
|
|
||
Осуществив предельный переход при t 0 и M , получим выражение для функционала распр д л ния вероятности белого гауссовского
|
|
|
т |
к |
|
|||
шума на интервале времени 0,T |
: |
|
||||||
|
|
о |
|
|
|
|
|
|
|
|
|
|
1 |
T |
|
||
F n( t ) h0 exp |
|
n( t ) 2 dt , |
(11.27) |
|||||
|
и |
|
N |
0 0 |
|
|
||
|
|
|
||||||
л |
|
|
|
|||||
|
|
|
|
|
|
|
||
где h0 – неопреде енная (бесконечно малая) константа, не зависящая от ста- |
||||||||
б |
|
|
|
|
|
|
|
|
тистических свойств случайного процесса. |
|
|||||||
и |
|
|
|
|
|
|
|
|
11.5.2.2. Комплексное представление полосовых случайных про- |
||||||||
цессов |
|
|
|
|
|
|
|
|
Комплексное представление полосовых сигналов в подразд. 11.3 каса- |
||||||||
Бется детерминированных сигналов. В этом |
подразделе рассмотрим ком- |
|||||||
плексное представление полосовых стационарных случайных процессов. Предположим, что n( t ) является реализацией стационарного в широ-
ком смысле случайного процесса N( t ) с нулевым средним и спектральной плотностью мощности Sn( f ) . Примем, что спектральная плотность мощности равна нулю вне интервала частот, группирующихся около частот f0 ,
174

где f0 – |
центральная частота. Случайный процесс N( t ) называется узкопо- |
||||||||||||||||||||||||||||||||||||||
лосным случайным процессом, если |
ширина его |
|
|
полосы частот f намного |
|||||||||||||||||||||||||||||||||||
меньше |
|
|
f0 . С учетом этого условия реализация процесса n( t ) может быть |
||||||||||||||||||||||||||||||||||||
представлена в одной из трех форм, а именно: |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
n(t) a(t)cos 2 f0t (t) ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(11.28) |
|||||||||||||||||||
|
n(t) nI (t)cos 2 f0t nQ (t)sin 2 f0t ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
(11.29) |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
( t )e |
j2 f |
|
t |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(11.30) |
||||
n( t ) Re n |
z |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Р |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
nz ( t ) nI ( t ) jnQ( t ), |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(11.31) |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
||
где a( t ) |
– |
|
огибающая, a |
|
|
( t ) – фаза вещественного сигнала, |
|
nI ( t ) , nQ( t ) – |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
квадратурные компоненты и nz ( t ) – комплексная огибающая процесса n( t ) . |
|||||||||||||||||||||||||||||||||||||||
Определим автокорреляционную функцию случайного процесса N( t ): |
|||||||||||||||||||||||||||||||||||||||
|
Rn ( ) N (t)N (t |
|
|
|
|
|
|
|
|
|
|
Б |
У |
|
|||||||||||||||||||||||||
|
|
|
nI (t)cos 2 f0t nQ (t) sin 2 f0t |
|
|
|
|
|
|
|
|
Г |
|
|
|
||||||||||||||||||||||||
|
|
|
|
n (t ) cos 2 f |
|
|
t n |
|
(t ) sin 2 f |
|
|
t |
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
0 |
|
0 |
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
I |
|
|
|
|
|
|
|
Q |
к |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
cos 2 f |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
2t |
|
(11.32) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
R ( ) R |
|
( ) |
|
|
R ( ) R |
( ) |
cos |
2 f |
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|||||||||||||||||||||||||||||
2 |
|
|
I |
Q |
|
|
|
|
|
|
|
0 |
|
|
I |
|
аQ |
|
|
|
|
0 |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
R ( ) R |
( ) |
sin |
2 f |
|
|
|
R ( ) R |
( ) |
sin 2 f |
0 |
2t |
, |
||||||||||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
о |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
где RI ( ), |
RQ( ) , RQI |
( ) |
и RQI |
( ) – автокорреляционные и взаимокорреля- |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
ционные функции квадратурных компонент случайного процесса n( t ) . |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
л |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Стационарность случайного процесса предполагает отсутствие зависи- |
|||||||||||||||||||||||||||||||||||||||
мости автокорре яц онной функции от абсолютного момента времени t , по- |
|||||||||||||
этому |
б |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||
|
2 и |
|
|
|
2 |
|
|
|
|
|
|
||
Rn ( ) |
N( t )N( t |
|
|
|
|
|
|
|
|
|
|||
|
1 |
R ( ) R ( ) cos 2 f |
|
|
1 |
R |
( ) R |
( ) sin 2 f |
|
, |
(11.33) |
||
|
0 |
|
0 |
||||||||||
|
|
I |
|
Q |
|
|
QI |
IQ |
|
|
|
||
Би, следовательно: |
|
|
|
|
|
|
|
|
|
||||
|
|
RI ( ) RQ( ) , |
|
|
|
|
|
|
|
|
(11.34) |
||
|
|
RQI ( ) RIQ ( ). |
|
|
|
|
|
|
|
|
(11.35) |
||
175

Таким образом, окончательное выражение для автокорреляционной функции случайного процесса записывается следующим образом:
Rn ( ) RI ( )cos(2 f0 ) RQI ( )sin(2 f0 ) . |
|
|
|
|
(11.36) |
||||||||
Автокорреляционная функция комплексной огибающей nz ( t ) опреде- |
|||||||||||||
ляется следующим образом: |
|
|
|
|
|
|
|
|
|||||
|
1 |
|
|
* |
|
1 |
RI ( ) RQ( ) jRQI ( ) jRIQ ( ) , |
||||||
Rz ( ) |
|
|
nz ( t )nz |
( t ) |
|
||||||||
|
|
|
|||||||||||
|
2 |
|
|
|
|
2 |
|
|
|
|
|
Р |
|
|
|
Rz ( ) RI ( ) jRQI ( ) . |
|
|
|
|
|
(11.37) |
|||||
Таким образом, |
автокорреляционная функция исходного случайного |
||||||||||||
|
|
|
|
|
|
|
|
|
|
У |
|
|
|
процесса n(t) определяется автокорреляционной функцией его комплексной |
|||||||||||||
огибающей nz (t) : |
|
|
|
|
|
|
Г |
И |
|
||||
|
|
R ( ) |
Re R ( )e j2 f0 . |
Б |
|
|
|
(11.38) |
|||||
|
|
|
n |
|
z |
|
а |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Взаимокорреляционная функция кв др турных компонент полосового стационарного случайного процесса удовлетворяет условию симметрии.
Кроме того, любая взаимокорреляционн я функция удовлетворяет условию |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
R |
|
( ) R |
к( ) . |
|
|
|
|
|
|
|
|
(11.39) |
||||||
|
|
|
|
|
|
следует |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
xy |
|
|
|
yx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
о |
|
|
|
, что RIQ( ) RIQ( ), то есть функция |
|||||||||||||||
Из этих особеннос ей |
|
|
|
|||||||||||||||||||
RIQ ( ) является нечетн |
й и RIQ ( 0 ) 0 . Из последнего следует, что квадра- |
|||||||||||||||||||||
|
|
ми |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
турные компоненты случайн го процесса являются некоррелированными при |
||||||||||||||||||||||
|
|
л |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
отсутствии между н |
|
|
временного сдвига. |
|
|
|
|
|
|
|
|
|
||||||||||
Когда стационарный случайный процесс N( t ) является гауссовским, |
||||||||||||||||||||||
квадратурные компоненты NI ( t ) |
и NQ( t ) совместно тоже гауссовские. |
|||||||||||||||||||||
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Более того, при 0 |
они статистически независимы, |
и, |
следовательно, их |
|||||||||||||||||||
совместнаябплотность вероятности |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Б |
|
|
|
1 |
|
|
|
n2 |
n2 |
|
|
1 |
|
|
* |
|
||||||
|
|
|
|
|
|
|
I |
Q |
|
|
|
|
n |
z |
n |
z |
|
|
||||
W( nI ,nQ ) |
|
|
|
exp |
|
|
|
|
|
|
exp |
|
|
, |
(11.40) |
|||||||
2 2 |
|
2 2 |
2 2 |
2 2 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
где дисперсия 2 определяется как 2 R |
( 0 ) R |
( 0 ) R ( 0 )). |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
I |
|
|
Q |
|
|
|
n |
|
|
|
Белый шум является случайным процессом, который имеет постоянную спектральную плотность в неограниченном диапазоне частот.
176

В вопросах, связанных с демодуляцией узкополосных сигналов на фоне шумов, математически удобно представить аддитивный шум как белый и выразить его через квадратурные компоненты. Это можно выполнить, предполагая, что сигнал и шум на приѐмной стороне прошли через идеальный полосовой фильтр, имеющий полосу пропускания более широкую, чем полоса сигнала. Такой фильтр может внести пренебрежимо малые искажения в сигнал, но он исключает частотные компоненты шума вне полосы пропускания фильтра.
|
Белый шум, прошедший через идеальный полосовой фильтр, называют |
|||||||||||||||||||||||||||||||
полосовым белым шумом. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Спектральная плотность мощности белого и полосового белого шума сим- |
|||||||||||||||||||||||||||||||
метрична относительно точки f |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Р |
||||||||||
|
0 , данная симметрия спектральной плотности |
|||||||||||||||||||||||||||||||
приводит к тому, что RIQ ( ) 0 |
|
для всех . Следовательно, |
|
И |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Rz ( ) RI ( ) RQ( ) Rn( ) . |
|
|
|
|
|
|
|
|
|
|
|
У |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Г |
|
|
||
|
Это означает, что квадратурные компоненты белого шума некоррели- |
|||||||||||||||||||||||||||||||
рованы при любых временных сдвигах . |
|
|
|
|
Б |
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
Таким образом, рассмотрение исходного случайного процесса в виде |
|||||||||||||||||||||||||||||||
белого гауссовского шума n( t ) |
может быть заменено рассмотрением его |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
||||||||
комплексного представления |
n( t ) n |
( t )e |
0 |
|
. При этом одномерная и мно- |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
к |
|
|
|
|
|
|
|
|
|
||||||
гомерная плотность распределения вероятности комплексных выборочных |
||||||||||||||||||||||||||||||||
|
|
nI 0 |
|
|
|
|
|
|
|
|
nIM jnQM может быть записана следую- |
|||||||||||||||||||||
значений n0 |
jnQ0 ,...,nM |
|
||||||||||||||||||||||||||||||
щим образом: |
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
о |
|
е |
|
|
|
|
|
|
|
|
* |
|
|
|||||||||||||||
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
nIi |
nQi |
|
|
|
|
n n |
|
||||||||||||||||||
W ( ni |
) W ( nIi ,nQi |
) |
|
|
|
exp |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
exp |
|
i i |
, |
(11.41) |
||||||
|
N0 |
|
|
|
|
|
N0 |
|
|
2 2 |
|
N0 |
||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|||||||||||||||
|
|
|
|
2 t |
|
|
|
|
|
2 t |
|
|
|
|
|
|
|
|
|
2 t |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
ли |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
M |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
M * |
|
|
|
|
||||
W ( n0 |
,...,nM |
) W ( ni ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
exp |
|
|
|
|
nini |
t . |
|
(11.42) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
N0 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
i 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N0 i 0 |
|
|
|
|
|||||||
иб |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
2 t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Соответственно функционал распределения вероятности для случая |
|||||||||||||||||||||||||||||||
непрерывного наблюдения можно записать |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
T |
|
|
* |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
F n( t ) h0 exp |
|
|
|
|
n( t )n ( t )dt |
. |
|
|
|
|
(11.43) |
|||||||||||||||||||
|
|
|
N0 |
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
177
Следует заметить, что приведенные выражения для многомерной плотности распределения вероятности комплексного представления белого гаус-
совского шума инвариантны к множителю e j2 f0t .
11.5.2.3. Функция правдоподобия для канала связи с аддитивным белым гауссовским шумом
Оценки компонент вектора информационных параметров 1,..., k
по методу максимума правдоподобия находятся как решение системы уравнений правдоподобия:
|
|
|
ln P( X |
|
|
,..., |
k |
) 0 , |
|
|
|
|
|
|
(11.44) |
|||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
Р |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
ln P( X |
|
,..., |
k |
) 0 . |
|
|
У |
|
(11.45) |
|||||||||||
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
k |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Г |
|
|
|
|
где P( X |
1,..., k ) P( X |
) – функция правдоподобия вектора параметров |
||||||||||||||||||||||
|
|
Б |
|
|||||||||||||||||||||
(многомерная плотность распределения вероятности |
выборочных значе- |
|||||||||||||||||||||||
ний x1,...,xn наблюдаемого процесса x( t ) ( |
ддитивной смеси полезного сиг- |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
е |
|
|
|
|
|
||
нала и помехи при условии конкр тныхазначений 1,..., k вектора информа- |
||||||||||||||||||||||||
ционных параметров ). |
т |
к |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Определим статистические свойства случайного процесса |
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
о |
x( t ) s( t, ) n( t ), |
|
|
|
|
|||||
где s( t, ) |
|
и |
|
|
|
|
|
|
|
|
|
|||||||||||||
– полезный с гнал, являющийся известной функцией времени и |
||||||||||||||||||||||||
|
|
|
|
|
|
|
сигнала |
|
|
|
|
|
|
|
|
|
|
|
||||||
вектора информац онных параметров ; |
n( t ) – белый гауссовский шум с |
|||||||||||||||||||||||
|
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
известной спектра ьной плотностью N0 / 2 . Считаем, что информационные |
||||||||||||||||||||||||
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
параметры |
|
|
|
|
|
|
известны. Зафиксируем момент времени и для него опре- |
|||||||||||||||||
дел м условное выборочное значение (при условии конкретного значения |
|
Б |
x s( ) n . |
информац онных параметров сигнала): |
|
Поскольку сигнал является известной функцией времени, то для его выборочного значения плотность распределения можно записать следующим
образом: |
|
Ws s s s( t, ) . |
(11.46) |
Плотность распределения вероятности выборочного значения шума является гауссовской:
178

W ( n ) |
|
1 |
|
|
|
|
n |
2 |
|
|
|
|
|
exp |
|
|
|
. |
(11.47) |
||||
|
|
|
|
|
|||||||
n |
2 2 |
|
|
|
2 2 |
|
|
||||
|
|
|
|
|
|
|
|
|
|||
Условная плотность распределения вероятности суммы двух независимых случайных величин s и n (при условии конкретного значения информационных параметров) находиться следующим образом:
|
|
|
|
|
|
Р |
|
Wx ( x |
) Ws ( x y )Wn ( y )dy Ws ( y )Wn ( x y )dy |
|
|
||||
|
|
|
|
|
И |
|
|
|
|
|
|
|
|||
|
y s( t , ) Wn ( x y )dy Wn x s( t , ) . |
|
|
|
(11.48) |
||
|
|
|
У |
|
|||
|
|
|
|
||||
|
|
|
|
|
|
||
|
|
|
Г |
|
|
|
|
Производя аналогичные преобразования для многомерного случая век- |
|||||||
|
|
|
Б |
|
|
|
|
тора выборочных значений процесса x( t ) на интервале времени 0,T , полу-
чим выражение для функции правдоподобия и ее предельного случая – функционала правдоподобия:
|
|
|
|
|
|
|
|
|
|
|
|
M 1 |
|
|
|
|
|
|
|
|
|
|
|
|
а2 |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
е |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
M |
|
|
|
|
|
|
|
|||||||
P( X |
) |
|
|
|
|
|
|
|
|
|
|
|
|
exp |
|
|
|
xi |
si ( ) t , |
|
|
(11.49) |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
N0 |
|
|
|
|
|
|
|
N0 i 0к |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
2 t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
F n( t ) |
|
h0 exp |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
x( t ) s( t , ) 2 dt , |
|
|
|
(11.50) |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
л |
|
|
N |
0 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
1 |
|
ti t / 2 |
|
|
|
|
|
1 |
ti t / 2 |
|
|
|
|
|
|
|
||||||||||||||||||||
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
) |
|
|
|
s( t , )dt |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
где x |
|
|
|
|
|
|
|
|
|
x( t )dt |
s ( |
|
|
|
|
|
|
– выборочные значения смеси |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
б |
и |
|
|
|
|
|
t ti t / 2 |
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
t ti t / 2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
сигнала |
|
шума и сигнала соответственно; M 1 – число выборочных значе- |
|||||||||||||||||||||||||||||||||||||
ний на рассматриваемом интервале времени |
0,T ; t |
– шаг дискретизации |
|||||||||||||||||||||||||||||||||||||
Б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
во времени. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
Аналогичные выражения получаются и для комплексного представле- |
|||||||||||||||||||||||||||||||||||||
ния полезного сигнала и шума |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
M |
|
|
* |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
P( X |
|
) |
|
|
|
|
|
|
|
|
|
|
exp |
|
|
|
|
( xi |
si |
)( xi si ) |
t . |
(11.51) |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
N0 |
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
N0 i 0 |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
179 |
Соответственно функционал распределения вероятности для случая непрерывного наблюдения можно записать
|
|
|
1 |
T |
|
|
|
|
* |
|
|
|
|
|
|
|
|||||||||
F x( t ) |
|
h0 exp |
|
|
( x( t ) s( t , ))( x( t ) s( t , )) |
dt |
, |
(11.52) |
||||
|
|
|||||||||||
|
|
|
N0 0 |
|
|
|
|
|
|
|
|
|
где знак обозначает комплексное представление соответствующего процесса, а * – операцию комплексного сопряжения.
Р |
|
квазиоптимальном |
|
11.5.3.1. Демодуляция информационного символа в целом |
|
информационныхИ |
па- |
раметров |
. Бу- |
дем считать, что на заданном интервале времениГ(Удлительность |
символа |
c |
|
модуляции) информационный параметр является постоянным и принимает |
|||||
одно из L известных значений ( L является размером ансамбля символов мо- |
|||||
дуляции). Например, |
|
|
к |
Б |
|
|
|
|
|
||
s(t, k ) A0cos( 0t k ) , |
е |
а |
|||
1 |
т2 |
|
|
|
|
где k – одно из возможных знач ний начальной фазы сигнала. |
|||||
о |
|
|
|
1 |
|
Конкретное значение информационного параметра соответствует кон- |
|||||
кретному значению симв ла передаваемой информации. Например, для слу- |
||||
чая L |
|
и |
|
|
2 значен е 0 и могут соответствовать передаче двоичной |
||||
«1» и двоичного «0», соответственно, |
или, при L 32 , значения |
0 , |
||
2 / 16 , 3 2 / 16 …, 32 31 / 16 |
могут соответствовать буквам |
ки- |
||
|
б |
|
|
|
риллицы. Схема кодирования может быть, в общем случае произвольной и |
||||
и |
|
|
|
|
определяетсялвидом модуляции. |
|
|
||
О щ м для всех видов модуляции является то, что каждому модули- |
||||
Б |
|
|
|
|
рующему с мволу ставится в соответствие свой конкретный несущий сигнал. Так в первом примере конкретным несущим сигналом для двоичной «1» является
s(t, ) s1 |
(t) A cos( t) , |
|
(11.53) |
|||
|
1 |
|
0 |
0 |
|
|
а для двоичного «0» |
|
|
|
|
|
|
s(t, ) s2 |
(t) A cos( t ) A cos( t ) . |
(11.54) |
||||
2 |
|
0 |
0 |
0 |
0 |
|
180

Таким образом, вне зависимости от схемы модуляции (вида модуляции) полезный сигнал может быть представлен как:
s1( t )
2 s(t, ) s ( t )
sL ( t )
1
2 . (11.55)
L
В соответствии с этим квазиоптимальный демодулятор должен сформировать (вычислить) L значений функции правдоподобия (для каждого
конкретного несущего сигнала) sk (t) |
|
|
|
|
|
|
|
|
|
|
Р |
|||||||||||
|
|
|
|
|
|
|
|
M 1 |
|
|
|
|
|
|
|
|
|
|
И |
|||
|
|
|
|
|
1 |
|
|
|
|
|
1 |
M |
|
|
k |
|
k * |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||
P( X |
|
|
k |
) |
|
|
|
|
exp |
|
|
|
|
( x |
s |
)( x |
Уs ) t |
|
. |
(11.56) |
||
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
i |
i |
i |
i |
|
|
|
||||
|
|
|
|
|
2 |
N0 |
|
|
|
|
|
N0 i 0 |
|
|
Г |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
2 t |
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|||
Множитель при экспоненте и |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
льн я плотность мощности шума |
||||||||||||||||||
наблюдения входят во все выражения для ч стных функций правдоподобия и |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
||
не оказывают влияние на поиск ма симального значения, на основании этого |
||||||||||||||||||||||||
функцию правдоподобия можно упростить: |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
спектр |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
е |
|
|
|||
|
|
|
|
|
|
|
|
|
|
1 |
M |
|
|
k |
|
k * |
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
P( X |
k |
) exp |
|
|
|
( xi |
si |
)( xi |
si ) |
t |
||||||||||||||
N0 |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
i 0 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
k |
|
|
|
т |
|
|
|
|
||||||||
exp |
|
M |
|
|
|
|
|
|
|
k * |
|
2 |
|
|||||||||||
|
|
( x |
s |
|
)( x |
|
|
s |
) /( 2 |
|
) . |
|
||||||||||||
|
|
|
|
i 0 |
i |
|
i |
|
|
|
i |
|
i |
|
|
|
|
(11.57) |
||||||
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
л |
|
|
t |
|
|
|
|
|
|
|
||||||||||
Множ тель |
|
|
1 |
|
|
практического значения для реализации алго- |
||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
||||||||||||||
|
б |
|
2σ |
|
|
|
|
N0 |
|
|
|
|
|
|
|
|||||||||
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ритма демодуляции не имеет, но оставлен для сохранения правильной размерности в математических выражениях.
Для уменьшения вычислительной сложности поиск максимума можно вести не между непосредственными значениями функции правдоподобия, а между любыми монотонными преобразованиями от нее (в частности, ее натурального логарифма), тогда оптимальная оценка информационного параметра определяется следующим образом:
181

* k max P( X |
|
), 1,..., L |
|
||
|
|
||||
|
M |
|
|
|
|
max (xi sik )(xi sik )* / (2 2 ), |
s s1,..., sL . |
(11.58) |
|||
|
i 0 |
|
|
|
|
В соответствии с полученной оценкой информационного параметра * (значения k , которое наиболее вероятно принимает информационный параметр в полезном сигнале, наблюдаемом совместно с шумом на интервале времени c ) и принятой схемой модуляции в дальнейшем производится декодирование принятого информационного символа.
11.5.3.2. |
|
|
Поэлементная демодуляция информационного символа |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Р |
При передаче цифровых сообщений каждому информационному сим- |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
|
волу (символу модуляции, конкретному несущему сигналу, представляюще- |
||||||||||||||||||
му информационный символ) соответствует двоичное число, содержащее K |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Г |
|
|
|
двоичных символов dm , где m – номер двоичного разряда, например в слу- |
||||||||||||||||||
чае 8-позиционной частотной манипуляции: |
Б |
|
|
|
||||||||||||||
d d |
d |
3 |
|
si (t) A cos( t) sd1d2d3 (t) |
|
|
|
|||||||||||
1 2 |
|
|
|
|
|
|
0 |
i |
|
|
|
|
|
|
|
|
|
|
000 |
|
|
s1 (t) A |
cos( t) s000 (t) |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
0 |
|
1 |
|
а |
|
|
|
|||
|
|
|
|
|
|
2 (t) A |
cos( |
|
|
|
|
|
||||||
001 |
|
|
s |
2 |
t) s001 |
(t) |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
0 |
|
|
к |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
010 |
|
|
s |
3 (t) A |
cos( t) s010 |
(t) |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
0 |
|
3 |
|
|
|
|
|
|
|
|
011 |
|
|
s |
4 (t) A |
е |
|
(t) |
|
|
|
|
|||||||
|
cos( |
4 |
t) s011 |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
100 |
|
|
s5 (t) A |
cos( t) s100 |
(t) |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
0 |
|
5 |
|
|
|
|
|
|
|
|
101 |
|
|
s |
6 |
(t) |
т |
|
|
|
101 |
(t) |
|
|
|
|
|||
|
|
A0 |
cos( 6t) s |
|
|
|
|
|||||||||||
110 |
|
|
s |
7о |
|
|
|
|
110 |
(t) |
|
|
|
|
||||
|
|
(t) |
A0 |
cos( 7t) s |
|
|
|
|
||||||||||
|
|
|
|
|
|
8 |
|
|
|
|
|
|
111 |
|
|
|
|
|
111 |
|
|
и |
A0 |
cos( 8t) s |
(t) |
|
|
|
|
||||||||
|
|
s (t) |
|
|
|
|
||||||||||||
|
|
л |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Сущность поэлементного приема (демодуляции) заключается в том, |
||||||||||||||||||
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
что демодулируется не значение информационного символа d1d2d3 непо- |
||||||||||||||||||
Бсредственнои с последующим его декодированием, а производиться оценка (демодуляция) непосредственно элементов dm , m 1,2,3... , составляющих
информационный символ.
При поэлементном приеме также применима методология синтеза решающих правил на основе максимума правдоподобия.
Поскольку каждый элемент информационного символа принимает только одно из двух возможных значений, то более удобным является использование не функции правдоподобия, а так называемого отношения правдоподобия, определяемого следующим образом:
182

|
|
|
|
|
|
|
1) |
|
|
|
|
|
|
P( X |
d |
m |
|
|
|||
|
|
L ( X ) |
|
|
|
|
, |
(11.59) |
||
|
|
|
|
|
|
|||||
|
|
|
m |
P( X |
dm |
0 ) |
|
|
||
|
|
|
|
|
|
|||||
|
dm 1) и |
|
dm 0 ) – функции правдоподобия (в общем случае |
|||||||
где P( X |
P( X |
|||||||||
апостериорные вероятности принятия элементом dm значений «1» и «0»),
соответственно.
Принятие решения о принятом значении элемента осуществляется в
соответствии со следующим правилом: |
|
|
|
Р |
|||
|
|
|
|
|
|
||
|
d |
* |
1, |
И |
|
||
0 |
|
|
|
||||
L ( X ) L |
m |
|
|
|
|||
m |
0 |
|
|
|
|
(11.60) |
|
L ( X ) L d |
* 0, |
У |
|
||||
m |
0 |
m |
|
|
|
|
|
где L – порог принятия решения. Для случая симметричного канала (равно-
вероятного принятия значений «1» и «0» рассматриваемым элементом dm и |
|||||||||
|
|
|
|
|
|
|
|
|
Б |
одинаковых потерь при искажении передаваемых «1» и «0») значение порога |
|||||||||
принятия решения равно L0 1. |
|
|
|
|
|
Г |
|||
С порогом можно сравнивать не непосредственно отношение правдо- |
|||||||||
|
|
|
|
к |
|
|
|||
подобия, а любое монотонное преобразов ние от него, в частности натураль- |
|||||||||
ный логарифм. Тогда для симметричного |
|
н ла правило принятия решения |
|||||||
можно переписать: |
|
|
е |
а |
|||||
|
|
т |
|
|
* |
1, |
|
||
|
ln Lm ( X ) 0 dm |
|
|||||||
|
|
|
|
|
|
|
|
|
(11.61) |
|
о |
( X ) 0 |
dm* |
0. |
|
||||
|
ln Lm |
|
|||||||
|
|
|
|
|
|
|
|
|
|
kи |
|
|
|
|
|
|
|
|
|
Учитывая несовместн сть событий присутствия на входе демодулятора |
|||||||||
л |
|
|
|
|
|
|
|
|
|
конкретных несущ х с гналов (одновременно передается только один сим- |
|||||||||
вол модуляции , соответственно, только один несущий сигнал sk ( t ) ),
апостериорная вероятность (функция правдоподобия) принятия значений «1» |
|||||||
и |
|
|
|
|
|
|
|
и «0» конкретным элементом может быть определена на основании теоремы |
|||||||
Б |
|
|
|
|
|
|
|
сумм рованбя вероятностей: |
|
|
|
|
|
||
|
|
dm 1) |
|
|
k ) , |
(11.62) |
|
|
P( X |
P( X |
|||||
|
|
|
k dm 1 |
|
|
|
|
|
P( X |
dm 0 ) |
|
P( X |
|
k ) . |
(11.63) |
|
|
|
k dm 0 |
|
|
|
|
Таким образом, при поэлементном приеме необходимо сформировать (вычислить) для каждого элемента dm свое отношение правдоподобия
183

|
|
|
|
k ) |
|
|
P( X |
|
|||
k dm 1 |
|
|
|
|
|
Lm( X ) |
|
|
|
(11.64) |
|
|
|
|
|||
|
|||||
|
P( X |
|
k ) |
||
|
k dm 0 |
|
|
|
|
и по результатам его сравнения с пороговым значением сформировать решение d*m о переданном значении элемента.
Проиллюстрируем полученное решающее правило на примере передачи трех рассмотренных выше элементных двоичных символов при условии
наблюдения сигнала на фоне белого гауссовского шума с заданными харак- |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Р |
|
теристиками. |
Запишем отношение правдоподобия для второго элемента d2 |
||||||||||||||||||||||||
модулирующего (информационного) символа d1d2d3 , |
|
И |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
M |
|
010 |
|
|
010 |
* |
|
|
|
У |
|
|
|||
|
|
|
|
|
|
|
|
|
|
( xi |
si |
|
)( xi si |
) |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
i 0 |
|
|
|
|
|
|
|
|
|
Г |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
P( X |
|
d |
|
|
M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
|
|
|
|||||||
|
2 1) exp |
|
|
|
|
2 2 |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
011 |
|
|
|
011 |
* |
|
|
|
|
110 |
|
110 |
* |
||||
|
|
|
|
|
( xi si |
|
)( xi si |
) |
|
а |
si |
)( xi si |
) |
||||||||||||
|
|
|
|
|
|
|
( xi |
||||||||||||||||||
|
|
|
|
|
i 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
exp |
|
|
|
|
2 2 |
|
|
|
|
exp |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 2 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
|
111 |
|
|
111 * |
|
|
к |
|
|
|
|
|
|
|
||||||||
|
|
( xi si |
|
)( xi si |
т |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
exp |
i 0 |
|
|
|
|
|
|
|
|
е, |
|
|
|
|
|
|
(11.65) |
||||||||
|
|
|
|
|
|
2 2 |
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
л |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
184

|
|
|
|
|
M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(xi si000 )(xi si000 )* |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
P( X |
d2 |
0) exp |
i 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
2 2 |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
|
|
|
|
|
|
|
|
|
|
M |
|
|
|
|
|
|
|||||
|
|
|
(xi |
si001 )(xi |
si001 )* |
|
|
|
|
|
|
|
|
|
(xi si100 )(xi |
si100 )* |
|
|||||||
|
|
|
i 0 |
|
|
|
|
|
|
|
|
|
|
|
|
i 0 |
|
|
|
|
|
|
|
|
exp |
|
|
|
|
|
|
exp |
|
|
|
|
|
|
|
||||||||||
|
2 2 |
|
|
|
|
|
2 2 |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(xi |
si101 )(xi |
si101 )* |
|
|
|
|
|
|
|
|
|
|
|
И |
|
||||||
|
|
|
i 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
exp |
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
(11.66) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
2 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
Р |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Г |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
1) |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
P( X |
d2 |
|
Б |
|
|
|
|
|
||||||||
|
|
|
|
|
L2( X ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
d2 |
|
|
|
, |
|
|
|
|
(11.67) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
P( X |
|
0 ) |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где xi − отсчеты комплексного предст вления входной смеси полезного сиг- |
|||||||||||||||||||||||
|
|
d d |
|
d |
|
|
|
|
компле |
|
|
|
|
|
|
c |
|
|
|||||
нала и шума; |
s 1 |
2 |
|
|
3 |
– отсчеты |
|
|
сного представления конкретного |
||||||||||||||
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
сигнала, несущего информационный символаd d |
2 |
d |
3 |
; M 1 – количество вы- |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
||
борочных отсчетов |
|
приходящихся |
на |
длительность |
|
|
информационного |
||||||||||||||||
|
|
|
|
|
|
|
|
т |
N |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
– |
|
дисперсия выборочных значений |
|||||||||
символа (символа модуляции); е |
|
||||||||||||||||||||||
ных представлен й |
|
процессов |
x( t ) и s |
1 2 3 ( t ) как координаты векторов на |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 t |
|
|
|
|
|
|
|
|
|
|
|
|
шума наблюдения. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d d |
d |
|
||||
|
|
оскости |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Если представ ть выб рочные значения соответствующих комплекс- |
|||||||||||||||||||||||
|
л |
|
|
|
|
d d |
d |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
комплексной п |
|
|
|
|
|
, то полученное правило принятия решения, по сути, |
|||||||||||||||||
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 2 |
|
3 ( t ), изображаю- |
|||
является прави ом поиска (выбора) того из сигналов s |
|
||||||||||||||||||||||
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
щий вектор которого максимально близок к входному процессу x( t ). |
|||||||||||||||||||||||
Б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11.6. Помехоустойчивость процесса демодуляции |
|
|
|||||||||||||||||||||
11.6.1. Общее соотношение для вероятности ошибочного приема
Будем считать, что на заданном интервале времени c (длительность
символа модуляции) информационный параметр является постоянным и принимает одно из L известных значений ( L является размером ансамбля символов модуляции).
185

Как отмечалось выше, вне зависимости от схемы модуляции (вида модуляции) полезный сигнал может быть представлен как
s1( t ) |
, |
|
||||
|
|
|
1 |
|
|
|
2( t ) |
|
|
, |
|
||
s |
2 |
|
||||
s(t, ) |
|
|
|
|
(11.68) |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L |
( t ) |
L , |
|
||
s |
|
|
||||
где |
|
и sk ( t ) |
Р |
|
k |
|
|
кретный несущий сигнал, представляющие k-й передаваемый информацион- |
||||||||||||||||||||||||||||||||
ный символ. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Демодулятор формирует (вычисляет) L значений функции правдопо- |
||||||||||||||||||||||||||||||||
добия (для каждого конкретного несущего сигнала) sk ( t ) |
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
M |
|
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|||||||
P( X |
) |
|
|
|
|
(x s k )(x s k )* / (2 2 ), |
k |
1,..., L, |
|
|
||||||||||||||||||||||
|
|
|
|
|
k |
|
|
|
|
|
|
i |
i |
|
|
|
|
i i |
|
|
|
|
|
|
|
|
У |
(11.69) |
||||
|
|
|
|
|
|
|
|
i 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Г |
|
|
||||||
|
|
|
|
|
|
|
M |
|
|
|
|
|
|
|
M |
|
|
|
|
M |
|
|
|
|
|
|
||||||
|
|
|
|
) |
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
* |
|
/ 2 2 . |
(11.70) |
||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
P( X |
|
|
|
|
x |
|
|
|
|
s |
|
|
2 Re x |
|
s k |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
|||||
|
|
|
k |
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
i |
|
|
|
|
|
i |
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i 0 |
|
|
|
|
i 0 |
|
|
|
|
i 0 |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
к |
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
|
|
|
|||||
Первые два слагаемых в выр жении для функции правдоподобия, |
||||||||||||||||||||||||||||||||
представляют собой величины, пропорциональные энергии смеси полезного |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
сигнала с шумом и энергии k-го н сущ го сигнала s |
|
(t). При условии равен- |
||||||||||||||||||||||||||||||
ства энергий несущих колебаний (случай симметричного канала связи) дан- |
||||
|
|
о |
||
ные слагаемые дают одинаковый вклад в итоговые значения функций прав- |
||||
|
и |
|
||
доподобия рассчитанных для конкретных сигналов sk (t). В соответствии с |
||||
|
|
|
k ) |
|
этим максимум |
P( X |
д стигается при достижении максимума третьим |
||
л |
|
|
|
|
M |
|
|
|
|
слагаемым Re xi sik * . |
Данное слагаемое представляет собой значение |
|||
б |
|
|
|
|
i 0 |
|
|
|
|
оценки ненормированного коэффициента корреляции между совокупностью выборочныхи значений входной смеси сигнала с шумом и k-го несущего сиг-
Бнала sk (t). Формально при определении несущего сигнала sk ( t ) , приводяще-
го к его максимизации функции правдоподобия при конкретном наблюдении входного процесса x( t ) демодулятор вычисляет L значений оценки ненор-
мированного коэффициента корреляции между совокупностью выборочных значений входной смеси сигнала с шумом и всех возможных несущих сигна-
лов sk ( t ) , k 1,...L и находит среди них максимальное. На основании данно-
го замечания определим среднюю вероятность ошибки приема информационного символа в целом.
186

Вероятность ошибки Pec определяется как взвешенная (с учетом априорной вероятности символов) линейная комбинация вероятностей ошибки (искажения) Pe( k ) каждого символа:
Pec |
1 |
L |
|
|
Pe( k ). |
(11.71) |
|
|
|||
|
L k 1 |
|
|
Обозначим значение ненормированного коэффициента корреляции между совокупностью выборочных значений входной смеси сигнала с шу-
мом и несущего сигналов sk ( t ) следующим образом:
|
|
M |
|
|
s |
k * |
|
c |
|
|
|
|
|
k |
* |
|
c |
|
|
|
k |
И |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
Z |
|
|
|
|
|
|
|
|
|
x( t )s |
( t )dt |
. |
|
(11.72) |
|||||||||||||||||||
k |
Re |
|
x |
|
|
|
|
|
|
Re |
x( t ) s |
|
( t ) dt |
|
|
|
|||||||||||||||||
|
|
|
|
|
i |
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Р |
|||||||
|
|
i 0 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Г |
|
|
|
|
||||
Определим вероятности ошибки Pe( k ) . Для этого сначала предполо- |
|||||||||||||||||||||||||||||||||
жим, что передавался, например, первый символ и определимУ |
вероятность |
||||||||||||||||||||||||||||||||
искажения при передаче первого символа Pe(1). |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
шума |
|
|
|
|
|
|
|
|
|
|
|
Вычисляемые |
|
значения |
|
Zk |
|
являются случайными величинами, по- |
|||||||||||||||||||||||||||
скольку в их формировании участвует шум н блюденияБ |
, входящий во вход- |
||||||||||||||||||||||||||||||||
ную смесь x( t ) . Гауссовский хара тер |
|
н блюдения и линейные опера- |
|||||||||||||||||||||||||||||||
ции формирования значений Z |
|
е |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
позволяют сделать заключение, что данные |
||||||||||||||||||||||||||||||||
случайные величины также |
|
|
|
|
|
подчинятьсяк |
гауссовскому закону распре- |
||||||||||||||||||||||||||
деления вероятности. |
k |
|
будут |
|
|
1 |
k |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Найдем математические ожидания случайных величин Zk : |
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
c |
и |
|
|
|
|
|
c |
n( t ) s ( t ) s ( t )dt |
|
|
|
|
|
|
|
||||||||||||||
|
|
Zk |
|
|
x( t )s ( t )dt |
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
0 |
л |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s1( t )sk ( t )dt Ec 1k , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(11.73) |
|||||||||||||||||
иk |
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Б |
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где Ec s |
( t )s |
|
|
( t )dt |
|
k |
m |
– энергия, |
приходящаяся на один информаци- |
||||||||||||||||||||||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
онный символ (для симметричного канала одинакова для всех передаваемых
|
|
|
|
символов); 1k |
1 |
c s1( t )sk ( t )dt – нормированный коэффициент корреля- |
|
E |
|||
|
0 |
||
|
c |
ции между первым и k -м несущими сигналами.
187

Аналогично находятся коэффициенты ковариации между случайными величинами Zk :
|
cov( Zk ,Zm ) Zk Zm Zk |
|
Zm |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
c |
|
c n( t ) s1( t ) sk ( t ) n( u ) s1( u ) sm ( u )dtdu |
Ec2 1k 1m |
|
|
|
|||||||||||||||||||
|
|
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
c |
c sk ( t )sm ( u ) n( t )n( u ) dtdu c |
|
c sk ( t )sm ( u ) |
N0 |
( t u )dtdu |
|
||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||
|
|
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
2 |
|
|
Р |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
N0 Ec |
km , |
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
(11.74) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
где |
km |
1 |
|
c sk |
( t )sm( t )dt – |
|
нормированный |
коэффициент |
корреляции |
||||||||||||||||||
E |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
между k -м и m -м несущими сигналами. |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
Коэффициенты cov( Zk ,Zm ) образуют корреляционнуюУматрицу мно- |
||||||||||||||||||||||||||
гомерной случайной величины |
Z1, Z2 ,...,ZL . |
Г |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
|
|
|
После того как таким образом определены статистические характери- |
||||||||||||||||||||||||||
стики случайных величин Zk , легко н йти вероятностьБ |
ошибки Pe(1) или ве- |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
к |
|
|
|
|
|
|
|
|
||
роятность правильного приема |
Pпр(1) 1 Pe(1) |
первого информационного |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
|
||||
символа. Она равна вероятности того, что величина Z1 |
будет иметь большее |
||||||||||||||||||||||||||
значение, чем величины |
остальных |
знач ний Z2 , Z3 ,...,ZL . |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
о |
|
|
|
Z1 |
|
Z1 |
|
|
|
|
|
|
|
|
||
|
Pпр |
(1) P Z1 |
max Zk |
|
... W( Z )dZ2 ...dZL dZ1 , |
|
|
(11.75) |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
k 1,...,L |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
л |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
где |
W( Z ) W( Z1 |
, Z1,...,ZL ) – L -мерная нормальная плотность вероятности с |
|||||||||||||||||||||||||
|
|
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Zk . Следу- |
||||||||
корреляционной матрицей cov( Zk ,Zm ) и средними значениями |
|||||||||||||||||||||||||||
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|||||
ет |
меть в в ду, что для некоторых наборов несущих сигналов s |
|
( t ) матри- |
||||||||||||||||||||||||
Б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ца коэфф ц ентов ковариации является сингулярной. Это означает, что невозможно определить многомерную гауссовскую плотность распределения вероятности W( Z ) ввиду однозначного определения одних случайных вели-
чин Zk другими.
Осуществив ряд замен переменных интегрирования, произведем дальнейшую формализацию выражения для вероятности правильного приема.
188

|
|
|
|
|
|
|
|
|
|
vk |
Zk Zk |
, |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
v1 Z1 Z1 |
Z1 v1 Z1 , |
|
|
|
|
|
||||||||||||||||
|
Pпр (1) |
dvk dZk , |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
Zk |
vk |
, |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
Zk Z1 vk v1 Z1 |
Zk |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
v1 |
Z1 |
Z2 |
|
v1 Z1 |
ZL |
|
|
|
|
|
|
|
|
|
(11.76) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
Р |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
... |
|
|
|
|
|
|
|
|
w(V)dv2 ...dvL dv1 . |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
uk 2 / (Ec N0 )vk |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Pпр (1) |
|
duk 2 / (Ec N0 )dvk |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
uk |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
vk |
|
|
|
|
|
|
|
|
|
|
И |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
vk v1 Z1 |
Zk |
|
uk |
u1 2 / (Ec N0 )( Z1 |
|
Zk |
) |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Г |
|
|
|||
|
u1 2/( Ec N0 ) ( Z1 Z2 ) |
|
u1 2/( Ec N0 ) ( Z1 ZL ) |
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
... |
|
|
|
|
|
|
|
|
|
|
wн (U)du2 ...duL du1 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(11.77) |
||||
|
Z1 Zk |
|
Ec (1 1k ) |
|
|
к |
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
|
||
|
u1 2 Ec |
/ N0 (1 12 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
u1 2 Ec / N0 (1 1L ) |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
... |
|
|
|
|
|
|
|
|
wн (U)du2 ...duL |
du1 , |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
где w( V ) – L -мерная гауссовская плотность распределения вероятностей с |
||||||||||||||||||||||||||||||||
корреляционной |
матрицей, состоящей из элементов cov( Zk ,Zm ) и нулевым |
|||||||||||||||||||||||||||||||
вектором средних значений; |
w (U) – L-мерная гауссовская плотность рас- |
|||||||||||||||||||||||||||||||
|
|
л |
|
|
|
|
|
|
|
|
н |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
пределен я вероятностей с нормированной корреляционной матрицей, со- |
||
|
б |
и нулевым вектором средних значений. |
стоящей з элементов km |
||
Таким образом, вероятность правильного приема первого символа бу- |
||
дет равна |
|
|
Б |
|
|
189

Pпр (1) 1 Pe (1)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
1 |
|
|
|
|
|
|
u1 2Ec / N0 (1 12 ) |
|
|
||||||||
|
|
|
|
|
( |
|
|
|
|
|
|
... |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
( 2 )L / 2 |
|
ρ |
|
1 / 2 |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
(11.78) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
u1 2Ec / N0 (1 1L ) |
|
1 |
|
T |
|
1 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
exp |
|
u |
|
ρ |
u du2 |
...duL )du1 |
, |
|||||||
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||||||
где ρ – определитель нормированной корреляционной матрицы; ρ 1 – матрица, обратная нормированной корреляционной матрице.
|
|
|
Аналогичным образом могут быть получены выражения для вероятно- |
||||||||||||||||||||||||||||||||||||||||||
сти правильного приема Pпр (k) всех остальных символов и вероятностиР |
|||||||||||||||||||||||||||||||||||||||||||||
ошибочного |
|
приема |
|
для |
|
|
всех |
|
символов |
Pe( k ) 1 Pпр( k ) |
, определяющие |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
L |
|
|
И |
||
общую вероятность ошибки приема символов Pc |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
P ( k ). |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
|
|
L |
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k 1 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Г |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|||||
налов нормированная корреляционная матрица представляет собой единич- |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
11.6.2. Случай ортогональных сигн лов |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
Рассмотрим случай ортогональных несущих сигналов. Для таких сиг- |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
ную матрицу rm 0, k m . В этомкслучае вероятность правильного прие- |
|||||||||||||||||||||||||||||||||||||||||||||
ма, например, условно первого символа равна |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
о |
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
u 2 / 2 |
1 u1 2Ec / N0 |
|
|
u 2 / 2 |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
P (1) 1 P (1) |
|
|
|
|
|
|
|
|
e |
1 |
|
|
|
|
|
|
|
|
|
e |
|
|
k |
|
du |
k |
du |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
пр |
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
т |
|
2 |
|
|
|
|
|
|
|
|
|
|
1 |
||||||||||||||||
|
|
|
|
|
|
|
л |
2 |
|
|
|
|
|
|
k 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(11.79) |
|||||||
|
|
|
|
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
e x 2 / 2 F( x |
|
|
|
|
L 1dx , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
2Ec / N0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
иF( x ) |
|
1 |
|
|
x |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
где |
|
|
|
e y |
|
/ 2dy – функция распределения вероятности нормаль- |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
2 |
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Бной случайной величины с нулевым математическим ожиданием и единич- |
|||||||||||||||||||||||||||||||||||||||||||||
ной дисперсией. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
Следовательно, вероятность искажения первого символа равна |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Pe(1) 1 |
|
1 |
|
|
|
|
e x2 / 2 F( x |
2Ec / N0 |
L 1dx . |
|
|
(11.80) |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
190

Полученное выражение справедливо для любого из L используемых информационных символов. Поэтому Pe( k ) Pe(1) для k 1, 2,...,L . Соот-
ветственно, вероятность ошибки может быть определена следующим образом:
Pec |
1 |
|
L |
|
|
1 |
|
|
|
|
||||
|
|
Pe ( k ) |
|
|
LPe (1) Pe (1) |
|
||||||||
|
|
L |
|
|||||||||||
|
|
L k 1 |
|
|
|
|
|
(11.81) |
||||||
|
|
|
|
|
|
|
|
|
|
F( x |
|
L 1 dx . |
||
|
|
1 |
|
|
|
|
|
|
||||||
1 |
|
|
|
|
e x 2 / 2 |
|
|
|||||||
|
|
|
|
2Ec / N0 |
Р |
|||||||||
|
|
|
|
|
|
|
||||||||
|
2 |
|||||||||||||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Полученная вероятность ошибочного приема соответствует вероятно- |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
сти ошибочного приема информационного символа (символа модуляции), |
||||||||||||||
она удобна при передаче символов соответствующих, например, буквам алфавита или конкретным командам. Если передается последовательность независимых двоичных элементов (бит), группы из которых формируют информационный символ, более удобной мерой качества является вероятность
ошибочного приема отдельного бита. Если при ортогональных несущих сиг- |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
||
налах произошла ошибка, то может быть выбрано с одинаковой вероятно- |
||||||||||||||||||
стью любое из L 1 неправильных решений. |
Г |
|
||||||||||||||||
Б |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11.6.3. Переход от вероятности ошиб и на символ модуляции |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|||
к вероятности ошибки на эл м нт (бит) модуляции |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
к |
|
|
|
|
||||
Пусть информационный символ формируется группой из k бит, тогда |
||||||||||||||||||
|
|
|
|
|
|
|
е |
|
|
|
|
|
k |
. Если произошла |
||||
общее количество информационных символов равно L 2 |
|
|||||||||||||||||
ошибка при приеме симв ла, |
о вероятность того, что исказятся ровно m из |
|||||||||||||||||
k бит, составляющих |
|
|
|
л, равна |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
о |
|
Ckm |
|
Ckm |
|
|
|
|
|||||||
|
|
m / k |
|
Ckm |
|
|
|
|
|
|
||||||||
|
|
Pe |
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
(11.82) |
|
|
|
|
k |
|
|
k |
|
L 1 |
|
|
||||||||
|
|
симв |
|
|
2 |
|
1 |
|
|
|
|
|
||||||
|
|
|
|
|
Ckj |
|
|
|
|
|
|
|
|
|
||||
|
л j 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где C m |
k! |
|
– число возможных сочетаний из k |
элементов по m , |
||||||||||||||
|
|
|||||||||||||||||
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
иm!( k m )! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
т. е. наборов из m элементов, выбранных из данных k элементов, наборы, отличающиеся только порядком следования элементов (но не составом), считаются одинаковыми.
Среднее количество искаженных бит при искажении символа модуляции определяется следующим образом:
191
|
|
k |
|
|
|
|
|
|
k |
|
iCki |
|
k 2 |
k 1 |
|
||
i / k |
|
i 1 |
|
|
|
|
||
mср iPe |
|
|
|
|
|
|
|
|
k |
|
k |
1 . |
(11.83) |
||||
i 1 |
|
j |
2 |
|
||||
|
|
Ck |
|
|
|
|
|
|
j 1
Таким образом, средняя вероятность искажения одного бита при ошибочном приеме символа модуляции равна
Peбит |
mср |
|
2k 1 |
. |
(11.84) |
|
|
||||
|
k |
2k 1 |
|
||
Для упрощения понимания изложенных выше соображенийРрассмотрим пример определения условной вероятности искажения конкретного бита
при искажении принятого информационного символа. |
|
И |
|||||
Правильная комбинация : |
000 |
|
|
|
|
||
|
|
|
У |
||||
|
|
|
|
|
|
||
Ошибочные комбинации : |
001 |
ошибка в одном символеГ |
|
||||
|
|
010 |
ошибка в одном символе |
|
|
||
|
|
|
|
|
Б |
|
|
|
|
011 ошибка в двух символах |
|
|
|||
|
|
100 |
ошиб в одном символе |
|
|
||
|
|
101 |
|
а |
|
|
|
|
|
ошиб а в двух символах |
|
|
|||
|
|
|
|
к |
|
|
|
|
|
110 ошибка в двух символах |
|
|
|||
|
|
111 |
ошибкаев трех символах |
|
|
||
В случае |
чн |
приема символа 000 имеется 7 возможных равно- |
|||||
|
|
т |
|
|
|
|
|
вероятных ош бочных к мбинаций, из которых три комбинации отличаются |
|||||||
|
го |
|
|
|
|
|
|
от правильной то ько в одном элементе, три – в двух элементах и только од- |
|||||||
ошиб на искажаетблвсе э ементы. Следовательно, можно определить вероятность
искажения одного, двух и трех элементов:ивероятность искажения одного элемента – 3/7;вероятность искажения двух элементов – 3/7;вероятность искажения трех элементов – 1/7.
Обратим внимание на то, что искажение одного элемента из трех соот-
ветствует вероятности ошибки 1/3; искажение двух элементов из трех соот- |
||||||
Б |
|
|
|
|
|
|
ветствует вероятности ошибки 2/3; искажение трех элементов из трех воз- |
||||||
можных соответствует вероятности ошибки 3/3. |
|
|
||||
Таким образом, средняя вероятность ошибки с учетом вероятностей |
||||||
искажения |
одного, |
двух |
и |
трех |
элементов |
составляет |
1/3 3/7+2/3 3/7+3/3 1/7 0,571 (1 3/7+2 3/7+3 1/7)/3.
192

При этом среднее количество искаженных символов
1 3/7+2 3/7+3 1/7=1,714.
Рассчитанное таким образом значение вероятности ошибки соответ-
ствует значению, определяемому в соответствии с |
2k 1 |
|
при k 3. |
|
2k 1 |
||||
|
|
|||
С учетом вероятности ошибочного приема информационного символа, состоящего из k бит (элементов) имеем вероятность ошибки приема отдельного бита
Pb |
2 |
k 1 |
Pc |
|
2 |
k 1 |
1 |
1 |
|
|
e x 2 / 2 F( x |
|
|
|
|
L 1 dx |
|
|
|
|||||||||
|
|
|
|
|
|
|
2E |
c |
/ N |
0 |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
e |
|
2k 1 |
|
e |
|
2k 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
(11.85) |
|||||||||||
|
2k 1 |
1 |
1 |
e x 2 / 2 F( x |
|
|
|
|
2k 1 dx |
|
|
|
|
Р |
||||||||||||||
|
|
2kE / N |
0 |
, |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
||||||
|
2k 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
|
||
где Eb Ec / k – энергия, приходящаяся на один бит передаваемой информа- |
||||||||||||||||||||||||||||
ции. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
На рис. 11.6 и 11.7 приведены зависимости вероятностиУ |
ошибочного |
|||||||||||||||||||||||||||
приема одиночных бит от отношения энергии, приходящейсяБГ на один бит передаваемой информации, к спектральной плотности мощности шума наблю-
дения Eb / N0 и от отношения энергии, приходящейся на один информационный символ, к спектральной плотности мощности шума наблюдения Ec / N0
при различной длине информационного |
символа |
k log |
2 |
L. |
|
Беглый взгляд на привед |
кзависимости оставляет противоречивое |
||||
ощущение: в соответствии с одними зависимостями лучшей помехоустойчи- |
|
востью (меньшей вероя |
нные |
ью ошибочного приема при одинаковом отно- |
|
шении сигнал/шум) бладают схемы модуляции с большим количеством ин-
формационных симв л в L 2k , а в соответствии с другими – наоборот. Ес- |
|
ли здесь противореч е? |
т |
нос |
|
Во-первых, с едует обратить внимание на то, что на обоих рисунках |
|
кривые для с учая бинарной модуляции ( k 1) совпадают. Различия возни- |
|
|
и |
л |
|
б |
|
кают для так называемых многопозиционных методов модуляции. Чтобы разобратьсяис данными различиями проанализируем полученные зависимо-
сти подробнее. Б
193
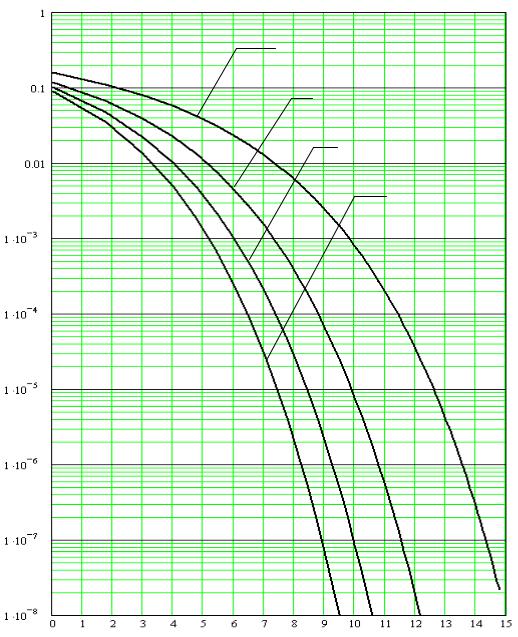
|
Pb |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k = 1 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k = 2 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
k = 3 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k = 4 |
Р |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
Г |
|
|
|
|||
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|||
|
|
|
|
|
|
|
а |
|
|
|
|
|
|||||
|
|
|
|
|
|
к |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
л |
|
|
|
|
|
|
|
|
|
|
|
|
Eb / N0 |
, дБ |
||
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 11.6. Зависимость вероятности ошибки от отношения сигнал/шум |
|||||||||||||||||
Энерг я, приходящаяся на один информационный символ, |
Ec Ps c , |
||||||||||||||||
Б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
численноиравна произведению мощности несущего данный символ сигнала Ps на его длительность c . В случае, когда информационный символ пред-
ставляет один передаваемый элемент (бит), вся эта энергия затрачивается на передачу данного бита, т. е. Ec Eb и c b . В случае, когда информацион-
ный символ представляет k элементарных бит, энергия Ec распределяется между несколькими элементами и Eb Ec / k , при этом возрастает в k раз количество переданных элементов (бит) за интервал времени c , т. е. одна и та же энергия Ec затрачивается на перенос значительно большего количества
194

информации, что закономерно ухудшает качество (помехоустойчивость) данного переноса. В то же время, если сравнивать различные схемы модуляции при фиксированной энергии, приходящейся на один элементарный бит Eb , увеличение количества элементов, которые представляет информацион-
ный символ, приводит к увеличению энергии несущего сигнала Ec kEb , что при, например, фиксированной длительности c эквивалентно повышению мощности Ps , т. е. кажущееся повышение помехоустойчивости (рис. 11.6) с ростом величины k эквивалентно ухудшению чувствительности демодуля-
тора. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Р |
|
|
Pb |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
||
|
|
|
|
|
|
|
|
|
|
k = 1 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
k = 2 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Г |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
Б |
k = 3 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
k = 4 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
к |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
л |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ec / N 0 , дБ
Рис. 11.7. Зависимость вероятности ошибки от отношения сигнал/шум
195
11.7. Основные методы дискретной модуляции
11.7.1. Фазовая манипуляция (PSK)
11.7.1.1. Бинарная фазовая манипуляция (BPSK)
Бинарная фазовая манипуляция – вид дискретной модуляции, при которой радиосигнал в общем виде может быть представлен следующим образом:
|
|
|
Р |
s(t) A0 gF (t k b )cos 0t υ0 Ck , |
(11.86) |
||
k 0 |
|
|
|
где A0 , 0 , 0 – амплитуда, центральная частота и начальная фаза несущего |
|||
|
|
У |
|
колебания; – принятая девиация фазы; Ck 1 – последовательность, со- |
|||
|
Г |
|
|
ответствующая передаваемым информационным символам И«0» и «1» (обыч- |
|||
но +1 соответствует «0», а–1 представляет «1»); gF ( t ) 0 t 0, b – фор- |
|||
|
Б |
|
|
мирующий импульс; b – длительность информационного символа (бита); k |
|||
– текущий номер передаваемого информационного символа. |
|
||
основных процедур при демодуляции сигналов далее будем считать, что |
|||
Примечание. Длительность формирующего импульса может превос- |
|||
к |
|
|
|
ходить длительность информационного символа, при этом |
происходит |
||
наложение передаваемых символов друг на друга. Для упрощения понимания |
||||
|
|
общем |
|
|
длительность формирующего импульса соответствует длительности мо- |
||||
дулирующего символа. |
т |
|
|
|
|
|
|
|
|
Формирующий импульс в |
|
случае может иметь произвольную |
||
о |
|
пилообразную и пр.) gF ( t ) . Обычно |
||
форму (прямоугольную, реугольную, |
||||
и |
|
|
|
|
форма импульса выбирается исходя из требований к форме спектра форми- |
||||
руемого радиос гнала ли прямоугольной. Влияние длительности и формы |
||||
формирующего мпульса будет рассмотрено позже в подразд. 11.8, посвя-
|
|
б |
щенном спектра ьным характеристикам модулированных радиосигналов. |
||
|
Пример временной функции, соответствующей радиосигналу при |
|
и |
||
услов |
|
девиациилфазы, равной / 2, и прямоугольной формы формирую- |
щего |
|
мпульса, приведен на рис. 11.8. |
Б |
|
|
196

S(t)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Р |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
Рис. 11.8. Форма радиосигнала с BPSK |
|
|
|||||||||||||
|
|
Комплексное представление радиосигнала с BPSK можетИбыть опреде- |
|||||||||||||||||||||
лено следующим образом: |
|
|
|
|
|
|
|
|
Г |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
Ck gF ( t k b )cos cos 0t |
|
|
|
|
|
|||||||||||||||
|
|
k 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|||
s( t ) A0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
к |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ck gF ( t k b ) sin sin 0t |
|
|
|
|
|
|
|||||||||||||||
|
|
|
k 0 |
|
|
|
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
|||
SI ( t )cos 0t SQ ( t ) sin 0t |
; |
|
|
|
|
|
|
|
|
(11.87) |
|||||||||||||
|
|
|
|
|
|
|
|
о |
|
; |
|
|
|
|
|
|
|
|
|||||
SI ( t ) A0 |
gF ( t k b |
)cos Ck |
|
|
|
|
|
|
|
(11.88) |
|||||||||||||
|
|
k 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
) sin C |
; |
|
|
|
|
|
|
|
|
|||
S |
Q |
( t ) A |
g |
F |
( t k |
b |
|
|
|
|
|
|
|
(11.89) |
|||||||||
|
0 |
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
k 0 |
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos t C |
|
|
|||||||
|
|
s (t) SI (t) jSQ (t) e j 0t |
|
|
|
|
|
|
0 k |
|
|
||||||||||||
|
|
Ao gF (t k b ) |
|
|
|
||||||||||||||||||
|
|
и |
л |
|
|
|
|
|
|
|
k 0 |
|
|
j sin 0t Ck |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(11.90) |
Б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
)e jCk e j 0t . |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
бA g (t k |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
0 k 0 |
F |
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Комплексная огибающая сигнала с бинарной фазовой манипуляцией полностью определяется его квадратурной и синфазной компонентами и представляется следующим выражением:
S(t) A0 |
|
(t k b )e jCk A0 |
|
(t k b ) cos Ck jsin Ck . (11.91) |
gF |
gF |
|||
|
k 0 |
|
k 0 |
|
|
|
|
|
197 |

Векторная диаграмма сигнала с бинарной фазовой манипуляцией пред- |
||||||||||||||||||||||||
ставлена на рис. 11.9. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
jy |
|
|
|
|
|
|
|
0t |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
Р |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
|
|
|
|
|
|
Рис. 11.9. Векторная диаграмма сигнала с -BPSK |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
|
|
||
При квазиоптимальном приеме решение (решающее правило при демо- |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Г |
|
|
|
||
дуляции) принимается на основании наблюдения входной смеси сигнала и |
||||||||||||||||||||||||
шума на интервале времени, соответствующем длительности b , с учетом |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
||
этого для интервала наблюдения на k -м интервале модуляции комплексная |
||||||||||||||||||||||||
огибающая может быть переписана в следующем виде: |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
|
||
S (t) A g |
|
|
(t k |
|
)e jCk |
A g |
|
к |
|
) j sin(C |
) |
|
|
|||||||||||
F |
b |
F |
(t k |
b |
) cos(C |
|
|
|||||||||||||||||
|
|
0 |
|
|
|
|
0 |
|
|
|
k |
|
|
k |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
|
|
|||
A0 gF (t k b ) cos( ) jCk |
sin( ) . |
|
|
|
|
|
|
|
|
|
|
(11.92) |
||||||||||||
|
|
|
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
|
|
||||
А соответствующой ей радиосигнал будет иметь следующий вид: |
||||||||||||||||||||||||
|
|
|
|
|
и |
k |
|
) cos( )cos( t) C |
sin( )sin( t) . |
|
(11.93) |
|||||||||||||
|
|
s(t) A g |
F |
(t |
b |
|
||||||||||||||||||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
0 |
|
k |
|
|
|
0 |
|
|
||
|
|
л |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Так м образом, сигнал, несущий информацию о передаче двоичной |
||||||||||||||||||||||||
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
«1», можно записать как |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s1 (t) A0 gF (t k b ) cos( ) cos( 0t) sin( )sin( 0t) , |
|
|
(11.94) |
|||||||||||||||||||||
Б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и сигнал несущий информацию о передаче двоичного «0»: |
|
|
||||||||||||||||||||||
s0 (t) A0 gF (t k b ) cos() cos(0t) sin() sin(0t) . |
(11.95) |
Функционал правдоподобия, соответствующий передаче двоичной «1»:
198

|
|
|
b |
|
|
|
|
|
* |
|
|
|
1 |
|
1 |
|
|
1 |
|
|
|
|
|
|||||||||
P( X |
1) exp |
|
|
|
|
dt |
||||
|
|
|
|
|||||||
N0 |
X (t) S (t) |
X (t) S |
|
(t) |
|
|||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
b |
X (t) A0 gF (t k b ) cos( ) j sin( ) |
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
N0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
exp |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(11.96) |
||||||||
|
|
|
|
|
|
|
X (t) A0 gF (t k b ) cos( ) j sin( ) |
* |
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
dt |
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и передаче двоичного «0»: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Р |
|||||||||||||||||||||
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
* |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
И |
||||||
P( X |
0) exp |
|
|
|
X (t) S |
|
(t) |
X (t) S |
|
(t) |
|
dt |
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
N0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
|
||||
|
|
1 |
|
|
X (t) |
|
A0 gF (t k b ) cos( ) j sin( ) |
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
N0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
exp |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Г |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|||
|
|
X (t) A g |
|
(t k ) cos( ) j sin( ) |
* |
dt |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
F |
|
|
|
|
b |
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где X ( t ) – комплексная огибающая входной смеси полезного сигнала |
||||||||||||||||||||||||||||||||||||||||
и шума. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
к |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Решение о значении передаваемого информационного символа Ck на |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
е |
основании |
|
|
|
|
|
|
|
|
||||||||||
k -м шаге модуляции формируется на |
|
сравнения рассчитанных |
||||||||||||||||||||||||||||||||||||||
значений функционала |
|
(функции для дис ретного времени наблюдения) |
||||||||||||||||||||||||||||||||||||||
правдоподобия. |
|
|
|
|
|
|
|
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
P(X |
0) |
P(X |
1) |
Ck* 1 |
|
|
(передавался «0») |
|
|
(11.97) |
||||||||||||||||||||||||||
|
|
|
|
P(X |
|
0) P(X |
|
1) C* |
1 |
|
(передавалась «1») |
|
|
|
(11.98) |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
л |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
При демоду яц |
|
|
|
с гнала с BPSK особое внимание следует обратить |
||||||||||||||||||||||||||||||||||||
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
на точность восстановиения опорного колебания, используемого при квадра- |
||||||||||||||||||||||||||||||||||||||||
турном прео разовании частоты, для получения комплексной огибающей
входной |
полезного сигнала и помехи (рис. 11.10). |
|
||||
При квадратурном преобразовании частоты выполняются следующие |
||||||
соотношен я: |
|
|
|
|
|
|
смеси |
|
|
|
|
|
|
Б |
X |
I |
( t ) jX |
Q |
( t ) e j ( t ) I( t ) jQ( t ) , |
(11.99) |
|
|
|
|
|||
|
|
|
|
|
|
|
где X I ( t ) и XQ ( t ) – синфазная и квадратурная компоненты комплексной огибающей входной смеси полезного сигнала и шума; ( t ) – ошибка опор-
ного колебания квадратурного преобразователя частоты относительно несущего колебания полезного сигнала. Для правильного принятия решений при
199

демодуляции необходимо выполнение условия ( t ) 0 (условие когерентной демодуляции). Вопросы компенсации фазовой ошибки ( t ) будут рассмотрены позже.
Х |
|
ФНЧ |
I(t) |
|
|
|
|
|
|
x(t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Р |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos( 0t + (t)) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Г |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Х |
|
|
|
|
|
|
ФНЧ |
|
|
|
|
Q(t) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
-sin( 0t + (t)) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
к |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
Рис. 11.10. Квадратурный преобразователь частоты. |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Рассмотрим вероятность ошиб и. Определим элементы нормированной |
|||||||||||||||||||||||||||||||
корреляционной матрицы сигнала с BPSK. |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
о1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|||||||
|
|
|
|
|
|
1 |
|
b |
sk ( t )sm( t )dt |
1 |
b |
sk ( t )sm( t )dt ; |
|
|
|||||||||||||||||
|
|
|
|
иb |
0 |
|
|
|
|
Eb |
|
0 |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
km |
|
|
Eb |
|
0 |
|
т |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
11 22 |
|
|
A0 cos( )cos( 0t) |
|
A0 sin( ) sin( 0t) |
dt |
|||||||||||||||||||||||
|
|
E |
|
|
|||||||||||||||||||||||||||
и2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
л |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(11.101) |
|||||
Б |
1 |
|
A2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
б |
|
|
|
0 |
|
b |
|
1 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
Eb |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
где Eb A0 b .
2
200

|
|
|
|
|
1 |
b |
A cos( ) cos( t) A sin( ) sin( t) |
|
|||||||||||||||||||||
|
|
E |
|
|
|||||||||||||||||||||||||
12 |
|
|
|
|
|
21 |
|
|
|
0 |
|
|
|
|
|
0 |
|
0 |
|
|
|
0 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
b |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A0 cos( )cos( 0t) A0 sin( ) sin( 0t) dt |
|
(11.102) |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
1 |
|
A2 |
cos( ) cos( t) 2 |
sin( ) sin( t) 2 dt |
|
|||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
Eb |
0 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
0 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
1 |
|
A02 b |
cos(2 ) cos(2 ) |
; |
|
|
|
|
|
|
Р |
|||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
Eb |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
cos(2 ) |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
(11.103) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos(2 ) |
|
|
1 |
|
|
|
У |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вероятность ошибочного приема информационного символа (бита) |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Г |
|
||
можно определить на основании общего выражения для ошибкиИприема, по- |
|||||||||||||||||||||||||||||
лученного ранее: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u1 2Eb / N0 (1 12 ) |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1/2 ( |
|
|
|
|
uT ρ 1u du2 )du1. |
|
|||||||
|
|
|
|
|
Peb 1 |
|
|
|
|
|
|
|
exp |
|
(11.104) |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
(2 ) |
ρ |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
к |
|
|
|
|
|
|
||||
одинаковые слагаемые, предс |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
авляющие немодулированное несущее колеба- |
|||||||||||||||||||||||||||||
Рассмотрим бинарную фазовую манипуляцию с изменением фазы на |
|||||||||||||||||||||||||||||
/2. Если внимательно присмотр ться |
|
|
сигналам, несущим различные ин- |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
|
||||
формационные символы s1( t ) |
и s0( t ), то можно заметить, что они содержат |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
ние – A0 gF (t k b )cos( ) cos( 0t) |
и не зависящие от передаваемой инфор- |
||||||||||||||||||||||||||||
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
мации (т. е. не являющиеся н сителями информации). Наличие данных сла- |
|||||||||||||||||||||||||||||
гаемых привод т к не правданному расходу энергии радиосигнала и, как |
||
л |
|
|
следствие, к пон жен ю помехоустойчивости его приема. |
||
б |
0 |
0 |
Наибо ее це есообразным с точки зрения повышения энергетической |
||
эффективности метода модуляции является случай использования девиации |
|||
и |
( π/2-BPSK или просто BPSK). При этом неинформа- |
||
фазы равной / 2 |
|||
Б |
|
A cos( / 2)cos( t) 0 |
|
тивная составляющая |
радиосигнала |
|
и вся энергия |
расходуется на передачу информационных символов.
В этом случае комплексная огибающая радиосигнала на интервале k -го шага модуляции равна
S (t) A0 gF (t k b )e |
jCk |
|
|
|
|
|
|
|
2 |
A0 gF (t k b ) jCk |
sin |
|
|||
|
|
|
|
|
2 |
|
(11.105) |
|
|
|
jA0 gF (t k b ), Ck |
|
1 «0», |
||
jA0 gF (t k b )Ck |
|
|
|||||
|
jA0 gF (t k b ), Ck |
1 «1», |
|
||||
|
|
|
|||||
201

а нормированная корреляционная матрица будет иметь следующий вид:
|
1 |
1 |
(11.106) |
|
|
|
|
. |
|
|
1 |
1 |
|
|
|
|
|
||
Функционал правдоподобия, соответствующий передаче двоичной «1»:
|
|
|
|
|
|
|
|
|
1 |
b |
|
|
|
|
|
|
* |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
P( X |
1) exp |
|
|
|
|
|
|
X ( t ) S1( t ) X ( t ) S |
1( t ) dt |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
N |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
1 |
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
* |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
exp |
|
|
|
|
|
X ( t ) jA0 gF ( t k b ) X ( t ) jA0 gF ( t k b ) dt |
|
(11.107) |
|||||||||||||||||||||||||
|
N |
|
|
||||||||||||||||||||||||||||||
|
|
|
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Р |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
и передаче двоичного «0» |
|
|
|
|
|
|
|
|
|
У |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
* |
|
|
|
|
|||||||
P( X |
0 ) |
exp |
|
1 |
|
|
X ( t ) S |
0 ( t ) X ( t ) S 0( t ) |
dt |
|
И |
|
|
||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 0 |
|
|
|
|
|
|
|
|
Г |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
1 |
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
* |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
exp |
|
|
|
|
X ( t ) jA0 gF ( t k b ) X ( t ) jA0 gF ( t k b ) |
dt , |
(11.108) |
||||||||||||||||||||||||||
|
N |
|
|
||||||||||||||||||||||||||||||
|
|
|
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
||
|
– комплексная огибающая входной Бсмеси полезного сигнала и шу- |
||||||||||||||||||||||||||||||||
где X ( t ) |
|||||||||||||||||||||||||||||||||
ма. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
к |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Решение о значении передаваемого информационного символа C |
|
на |
|||||||||||||||||||||||||||||||
k-м шаге модуляции формиру тся на основании |
сравнения рассчитанных |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
значений функционала (функции для дискретного времени наблюдения) |
|||||||||||||||||||||||||||||||||
правдоподобия: |
|
|
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
оk |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
P(X |
|
|
|
|
|
|
и |
|
1 |
(передавался «0»); |
|
|
|
|
|
|
|
|
|||||||||||||||
0) P(X 1) |
C* |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
является |
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
P( X |
0) P( X 1) |
C* 1 |
(передавалась «1»). |
|
|
|
|
|
|
|
|
||||||||||||||||||||||
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Поско ьку |
|
|
нормированная корреляционная |
матрица |
сигнала |
с |
|||||||||||||||||||||||||||
π/2-BPSK |
|
|
|
|
|
|
|
|
|
|
сингулярной (вырожденной, |
|
|
0 ), общее выражение для |
|||||||||||||||||||
нахожден я вероятности ошибки непосредственно применено быть не мо-
жет. Это вызвано тем, что корреляционные интегралы находятся в следющей |
||||||||||||
зависимостии. |
|
|
|
|
|
|
|
|
|
|
|
|
Б M |
|
|
k * |
|
c |
|
k |
* |
c |
|
k |
( t )dt , k 0,1. |
|
|
|
x( t )s |
|||||||||
Zk Re xi si |
Re x( t ) s |
( t ) dt |
|
|||||||||
i 0 |
|
|
|
|
0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Однозначно определяют друг друга лишь Z1 Z2 . В этом случае сов-
местная плотность распределения вероятности случайных величин отличается от гауссовской и может быть записана следующим образом:
202
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
Z1 Z1 |
|
2 |
|
|
|
|
|
||||||||||||
W Z1 ,Z2 ( Z1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
Z2 ) |
|
|
|
|
|
|
|
|
|
|
exp |
|
|
|
2 2 |
|
|
, |
|
|
|
(11.109) |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
2 2 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где 2 |
N0 Eb |
и |
Z |
E . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
2 |
|
|
|
|
1 |
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
Z1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
Z |
Z |
|
2 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Peb 1 |
|
( Z1 Z2 ) |
|
|
|
|
|
|
|
|
|
exp |
1 |
1 |
|
dZ1dZ2 |
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 2 |
|
|
|
|
||||||||||||||||||||||||||
2 2 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Р |
|
0 |
|
|
|
1 |
|
|
|
|
|
|
|
Z |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Z1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
1 |
|
|
|
|
|
|
|
exp |
|
|
|
2 2 |
|
|
|
|
|
dZ |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
0 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
У |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
Z Eb |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
1 |
|
|
|
|
|
|
|
|
exp |
|
|
|
|
|
|
|
|
|
|
|
|
dZ . |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
N |
0 |
E |
|
|
|
|
|
N |
E |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Г |
|
|
(11.110) |
|||||||||||
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
0 b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Воспользуемся стандартной и модифицированной функцией ошибок |
||||||||||||||||||||||||||||||||||||||||||
соответственно: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
аerfc(x) 1 erf (x) , |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
x |
|
|
|
2 dt и |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
erf (x) |
|
|
e t |
|
|
(11.111) |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
к |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
тогда выражение для вероятности ошибочного приема можно перепи- |
||||||||||||||||||||||||||||||||||||||||||
сать так: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
E |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
тPb |
|
|
|
erfc |
|
|
|
b |
. |
|
|
|
|
|
|
(11.112) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
о |
e |
|
|
|
2 |
|
|
|
|
|
N0 |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
что |
π/2-BPSK |
метод модуляции |
обладает |
|||||||||||||||||||||||||
Необходимо отметить, |
||||||||||||||||||||||||||||||||||||||||||
наивысшей помехоустойчивостью. На рис. 11.11 изображены зависимости |
|||
|
|
л |
Eb / N0 для сигнала с π/2- |
вероятности оши очного приема от отношения |
|||
|
б |
|
|
BPSK с гнала с двухпозиционной модуляцией, использующего ортого- |
|||
и |
|
|
|
Б |
|
|
|
нальные несущие сигналы с одинаковой энергией (бинарная ортогональная модуляция). Высокая помехоустойчивость объясняется обеспечением максимально возможного расстояния между векторами, представляющими сигналы, несущие двоичные «1» и «0».
203
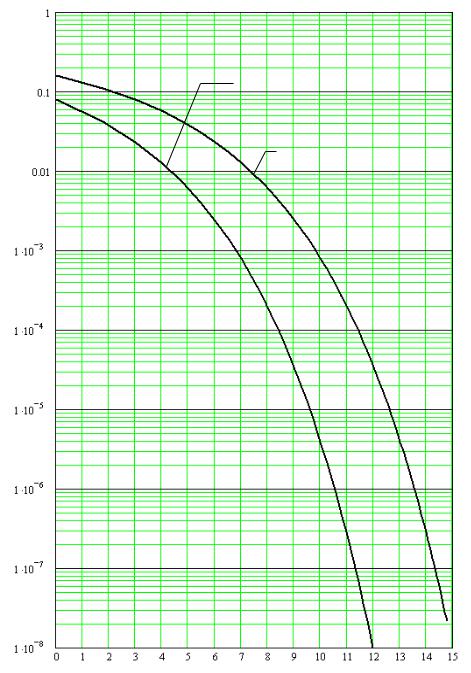
|
Pb |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
/2 BPSK |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
Ортогональная |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
модуляция |
|
|
Р |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
|
||
|
|
|
|
|
|
|
|
|
|
|
У |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
Г |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
к |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
л |
|
|
|
|
|
|
|
|
|
|
Eb / N 0 |
, дБ |
||
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Б |
Р с. 11.11. Сравнение помехоустойчивости сигналов с π/2-BPSK |
|||||||||||||||
|
|
и бинарной ортогональной модуляцией |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
||||||||||
204
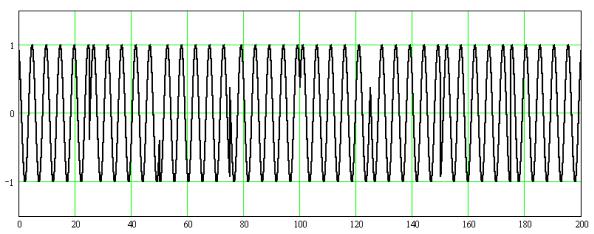
11.7.1.2.M-ичная фазовая манипуляция (M-PSK)
M-ичная фазовая манипуляция – вид дискретной модуляции, при которой радиосигнал в общем виде может быть представлен следующим образом:
|
|
s(t) A0 gF (t k c )cos 0t 0 (k) , |
(11.113) |
k 0 |
|
где A0 , 0 , 0 – амплитуда, центральная частота и начальная фаза несущего |
|
колебания; ( k ) – фазовый набег соответствующий передаваемой информа- |
||||||||||||||||||||
|
|
|
t 0, c – |
|
|
|
|
|
|
|
|
|
|
|
|
|
Р |
|||
ции; |
gF ( t ) 0 |
формирующий импульс; |
c – длительность ин- |
|||||||||||||||||
формационного символа; k |
– |
текущий номер передаваемого информацион- |
||||||||||||||||||
ного символа. Фазовый набег ( k ) |
|
|
|
|
|
|
|
|
|
И |
||||||||||
постоянен на интервале времени, совпа- |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
|
|
дающем с интервалом действия информационного символа и принимает одно |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Г |
|
|
||
из M |
известных значений |
|
(обычно |
|
|
2 ( m 1) |
). |
|
|
|||||||||||
|
|
|
|
|
|
|
|
m |
|
|
|
m |
|
|
M |
|
|
|
|
|
|
Пример временной функции, |
соответствующей радиосигналу 8-PSK |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|||
при прямоугольной форме формирующего импульса, приведен на рис. 11.12. |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
|||
S(t) |
|
|
|
|
|
|
|
|
|
к |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
л |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
||
|
и |
|
|
|
Рис. 11.12. Форма радиосигнала с 8-PSK |
|
||||||||||||||
Б |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Комплексное представление радиосигнала с M -ичной PSK может быть |
|||||||||||||||||||
определено следующим образом:
205

|
|
|
|
|
|
|
gF (t k c ) cos (k) cos 0t |
|
|||
s(t) A0 |
k 0 |
|
|
|
|
|
|
|
|
||
|
|
(t k c ) sin (k) sin 0t |
|
|
|
|
|
|
|||
|
gF |
|
|
||
|
|
k 0 |
|
|
|
SI (t) cos 0t SQ (t) sin 0t , |
|
|
|
|
(11.114) |
||||||
|
|
|
|
|
|
k c )cos ( k ) , |
|
|
|
||
|
|
|
|
SI ( t ) A0 |
gF ( t |
|
|
(11.115) |
|||
|
|
|
|
|
k 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
SQ ( t ) A0 gF ( t k c ) sin ( k ) , |
|
|
|
|
(11.116) |
|||||
|
|
|
|
k 0 |
|
|
|
|
|
|
Р |
|
|
|
|
|
|
cos t (k) |
|
||||
s (t) SI |
(t) jSQ (t) e j 0t |
|
|
0 |
|
|
|
||||
Ao gF (t k c ) |
|
|
|
||||||||
|
|
|
|
|
k 0 |
|
|
У |
|
|
|
|
|
|
j sin 0t (k) |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(t k |
|
)e j (k )e j 0t . |
|
|
|
|
И |
||
A g |
|
|
|
|
|
|
|||||
0 k 0 |
F |
|
c |
|
|
|
|
|
|
|
(11.117) |
Комплексная огибающая сигнала с многопозиционнойГ |
фазовой мани- |
||||||||||
пуляцией полностью определяется его квадратурной и синфазной компонен- |
|||||||||||||||||||
тами и представляется следующим выр жениемБ: |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
к |
|
|
|
|
|
|
|
|
||
S(t) A |
|
g |
|
(t k |
|
е |
|
cos |
(k) |
j sin |
(k) |
|
|
||||||
F |
)e j (k ) A |
|
gа(t k ) |
. |
(11.118) |
||||||||||||||
|
0 |
|
|
|
c |
|
|
0 |
|
F |
c |
|
|
|
|
|
|||
|
|
k 0 |
|
|
|
т |
|
k 0 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Векторная диаграмма сигнала («созвездие») с восьмипозиционной фа- |
|||||||||||||||||||
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
||||
зовой манипуляцией предс авлена на рис. 11.13. Информационные (модули- |
|||||||||||||||||||
рующие символы) |
m |
усл вно закодированы двоичным трехразрядным |
|||||||||||||||||
|
и |
|
|
|
|
|
|
|
|
|
|
Pb . |
|
||||||
кодом Грея |
уменьшения вероятности ошибочного приема |
Поскольку |
|||||||||||||||||
|
для |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
||
несущие сигна ы разл чных модуляционных символов являются коррелированнымиб, наи о ее вероятными являются ошибки восприятия соседних информационных символов, например 111 и 110 или 111 и 101. Приведенная схемаикод рования символов обеспечивает искажение только одного инфор- Бмац онного элемента (бита) при подобных наиболее вероятных ошибках.
206

jy |
010 |
|
0t |
|
|
||
011 |
|
|
110 |
001 |
|
m |
111 |
|
|
x
000 |
|
101 |
|
|
Р |
|
|
|
|
||
|
100 |
|
|
И |
|
|
|
|
|
||
|
|
|
У |
|
|
Рис. 11.13. Векторная диаграмма сигнала с 8-PSK |
|
||||
|
|
Г |
|
|
|
При квазиоптимальном приеме решение принимается на основании |
|||||
|
|
Б |
|
|
|
наблюдения входной смеси сигнала и шума на интервале времени, соответствующем длительности c , с учетом этого для интервала наблюдения на k -
м интервале модуляции комплексная огибающая может быть переписана в |
||||||||||||||||||||||||||||||
следующем виде: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
к |
|
|
|
|
|
|
||||||
|
|
|
S(t) A0 gF (t k c )e j (k ) |
е |
|
|
|
|
|
|
|
|
|
(11.119) |
||||||||||||||||
|
|
|
A0 gF (t |
k c ) cos( (k)) j sin( (k)) , |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
а соответствующий ей радиосигнал: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
s(t) A0 gF |
(t k c ) |
cos( (k)) cos( 0t) sin( (k))sin( 0t) . |
(11.120) |
||||||||||||||||||||||||
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Поскольку параметр ( k ) может принимать одно из возможных зна- |
|||||||||||||||||||||||||||||
чений |
|
|
л |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
m |
|
|
M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ний |
функции |
(функционала) правдоподобия |
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Б |
б |
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
* |
|
||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
m |
|
|
|
|
m |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
P( X |
m) exp |
|
|
|
|
|
S |
|
|
|
|
|
dt |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
N0 |
|
X (t) |
|
(t) |
X (t) S |
|
(t) |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
1 |
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
X (t) A0 gF (t k c ) cos( m ) j sin( m ) |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
N0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
exp |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
(11.121) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(t k |
|
) cos( |
|
|
) j sin( |
|
) |
* |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
||||||||||||
|
|
|
|
|
X (t) A g |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
0 |
F |
|
|
c |
|
|
|
|
|
m |
|
m |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где X ( t ) – комплексная огибающая входной смеси полезного сигнала и шума.
207

Решение о значении передаваемого информационного символа ( k )
на k -м шаге модуляции формируется на основании сравнения (нахождения максимального из рассчитанных значений) полученных величин функционала (функции для дискретного времени наблюдения) правдоподобия:
* (k) m max P( X k), k 1, 2, ..., M .
Правило принятия решения о значении передаваемого информационного символа может быть получено и без непосредственного формирования
(вычисления) значений функционала правдоподобия. Для этого формализуем |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k ), k 1, 2, ...,M следующим обра- |
||||||||||||||||
процедуру поиска максимума max P( X |
||||||||||||||||||||||||||||||||||||||||||
зом: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Р |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X ( t ) |
S( t , ) |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
У |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
||||||
|
|
P( X |
) |
|
|
|
|
exp |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 . |
|
(11.122) |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N0 |
|
|
|
|
|
* |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
0 X ( t ) S( t , ) |
* |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
Тогда правило принятия решения определится процедурой поиска та- |
||||||||||||||||||||||||||||||||||||||||
кого значения m информационного параметра сигналаГ, которое наиболее |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ла |
|
|
|
|
|
, m 1,...M . |
||||||||||||
«близко» к полученной оценке * |
или * (k) min |
* m |
||||||||||||||||||||||||||||||||||||||||
|
|
Поиск точки экстремума фун цион |
|
пр вдоподобия |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
к |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
X ( t ) S( t , ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
е* |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
exp |
N |
|
|
|
|
|
|
|
|
dt |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
0 0 |
|
X ( t ) S( t , ) |
|
|
* |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
чки |
экстремума функционала следующего вида |
||||||||||||||||||||||||||||||
равноценен по ску т |
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
X ( t ) S( t , ) X ( t ) S( t , ) * dt |
|
|
|
|
0 . |
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
0 |
л |
|
|
|
|
|
|
|
|
|
|
|
|
|
* |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
иПредставим полезный сигнал в следующем виде: |
|
|
|
|
|
|
e j , |
|||||||||||||||||||||||||||||||||
|
|
S( t, ) |
|
S( t, ) |
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
учитывая, что при рассматриваемом виде модуляции |
S( t, ) |
|
S( t ) |
не зави- |
||||||||||||||||||||||||||||||||||||||
сит от передаваемых информационных символов, имеем |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
X ( t )e j |
X * ( t )e j dt |
|
0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
* |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
208

|
|
|
|
|
|
|
|
Поскольку |
X ( t ) X I jXQ , окончательно получим |
|
|||||
|
c |
|
|
|
|
c |
|
|
cos( * ) XQ (t)dt sin( * ) X I (t)dt |
|
|||||
|
0 |
|
|
|
0 |
|
|
или |
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
XQ |
(t)dt |
|
||
|
* arctg |
0 |
|
|
|
|
(11.123) |
|
c |
|
|
|
|||
|
|
|
|
|
. |
||
|
|
|
X |
|
(t)dt |
Р |
|
|
|
|
I |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
И |
Полученное выражение определяет принцип работы квадратурного фа- |
|
зового детектора. |
У |
|
|
Точность восстановления опорного колебания, используемого при квадратурном преобразовании частоты для получения комплексной огибаю-
щей входной смеси полезного сигнала и помехи, |
оказывает существенное |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
||||
влияние на правильность принятия решений. При демодуляции необходимо |
|||||||||||||||||||||||||||||||
выполнение условия ( t ) 0 (условие когерентнойГдемодуляции). |
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
аc |
|
|
|
|
|
|
||||
Определим элементы нормированной корреляционной матрицы не- |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
к |
|
|
|
|
|
|
|
||||
сущих информационные символы сигн лов. |
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
sk ( t )sm( t )dt |
1 |
|
|
sk |
( t )sm( t )dt ; |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
(11.124) |
|||||||||||||||||||||
|
|
km |
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
Ec |
|
|
|
|
|
|
т |
|
Ec |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
c |
|
|
е |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
E |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
km |
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
A0 cos( k ) cos( 0t) A0 sin( k ) sin( 0t) |
|
|||||||||||||||||||
|
|
|
л |
|
|
|
|
c |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
A0 cos( m )cos( 0t) A0 sin( m ) sin( 0t) dt |
|
|||||||||||||||||||||||||
|
|
Aб |
1 |
|
|
A2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
0 |
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
и |
cos( k |
m ) cos( k m ) , |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
и |
|
|
|
|
|
Ec |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(11.125) |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где E |
|
0 c |
– энергия, приходящаяся на один информационный символ, |
||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||
c |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
1 |
|
|
|
|
|
|
|
|
cos( 1 2 ) |
|
|
|
cos( 1 M ) |
|
|||||||||||||||
|
|
cos( |
|
) |
|
|
|
|
1 |
|
|
|
|
|
cos( |
|
|
|
) |
|
|||||||||||
ρ |
|
|
|
2 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
M |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos( M 2 ) |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
cos( M 1 ) |
|
|
|
|
|
|
1 |
|
|
|
|
||||||||||||||||||
209

Нормированная корреляционная матрица сигнала с M-PSK является сингулярной (вырожденной) с 0. Общее выражение для нахождения ве-
роятности ошибки непосредственно применено быть не может.
Для нахождения вероятности ошибки рассмотрим подробнее правило принятия решения о передаваемом символе подробнее. Итак, демодулятор осуществляет поиск максимальной из рассчитанных величин
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
* |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
P( X |
m ) exp |
|
|
|
|
X ( t ) S m ( t ) X ( t ) |
S m ( t ) |
dt |
. |
|
|
|
|
|
(11.126) |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N |
0 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
Преобразуем данное выражение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
* |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Р |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
* |
|
|
|
m |
|
|
|
m |
|
|
|
|
|
|
|
m |
|
|
|
* |
|
|
|
|
|
|
|
|||||||
P( X |
m ) exp |
|
|
|
|
|
|
|
X ( t )X |
|
|
|
( t ) S |
|
|
( t ) S |
|
( t ) |
2 Re S |
|
( t )X |
|
( t ) dt |
|
. |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m соответствуетУпоиску |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
Поиск |
максимума |
|
P( X |
m ) |
по |
|
|
|
|
максимума |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
* |
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt Ec |
Г |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Re S m( t )X* ( t ) , поскольку |
|
|
S m( t ) S m( t ) |
|
и |
|
X ( t )X |
* ( t )dt |
не зави- |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
Б |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
сят от передаваемого информационного |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
Таким образом, корреляционный демодулятор проецирует принимае- |
||||||||||||||||||||||||||||||||||||||||||||||||
мый сигнальный вектор |
|
|
|
X I , XQ |
|
|
символа |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
X |
|
на М возможных сигнальных векторов |
||||||||||||||||||||||||||||||||||||||||||||||||||
m |
|
|
m |
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
к |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
S |
|
SI |
,SQ |
. Решение принима тся в пользу сигнала с наибольшей проек- |
||||||||||||||||||||||||||||||||||||||||||||||||
цией. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
Корреляционный де ек ор эквивалентен фазовому детектору, |
который |
|||||||||||||||||||||||||||||||||||||||||||||||
определяет фазу принимаем го сигнала |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
X ( t ) и выбирает сигнальный вектор |
||||||||||||||||||||||||||||||||||||||||||||||||||||
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
S |
( t ), фаза которого бл же всего к фазе |
X ( t ) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
Подтверд м данное утверждение. Корреляционный демодулятор вы- |
||||||||||||||||||||||||||||||||||||||||||||||||
числяет значенияфункций |
|
(функционалов) правдоподобия для всех возмож- |
||||||||||||||||||||||||||||||||||||||||||||||||||
ных |
|
|
ов, несущих различные информационные символы. Если внима- |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
л |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
тельно пр смотреться к структуре функционала, то можно увидеть операцию |
||||||||||||||||||||||||||||||||||||||||||||||||||||
выч слен я среднего (с точностью до постоянного множителя 1 / |
c |
) во вре- |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
мени расстояния между вектором входного процесса |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
X ( t ) и вектором кон- |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
сигна |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
кретного несущего сигнала |
|
S |
|
|
( t ): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
Б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
* |
|
c |
|
|
|
|
|
m |
|
|
|
|
2 |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
X ( t ) S m( t ) X ( t ) S m( t ) |
dt |
|
X ( t ) S |
( t ) |
|
dt |
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
210
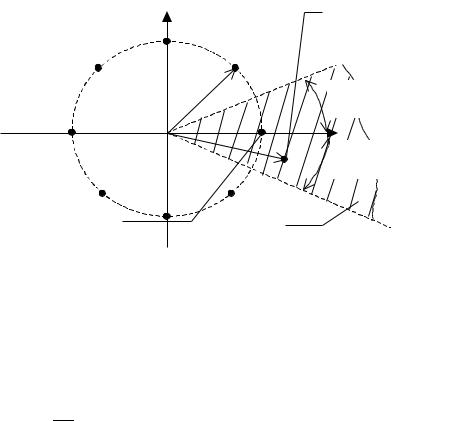
|
|
c |
|
|
|
|
|
m |
|
2 |
|
|
|
m |
|
2 |
|
|
(11.127) |
||
|
|
Re X ( t ) Re S |
( t ) |
Im X ( t ) Im S |
( t ) |
dt . |
|||||||||||||||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение о передаваемом символе принимается путем поиска мини- |
|||||||||||||||||||||
мального из всех возможных определенных расстояний. Геометрически это |
|||||||||||||||||||||
интерпретируется следующим образом (рис. 11.14). Из рисунка видно, что |
|||||||||||||||||||||
определение минимального расстояния между каждой из точек, представля- |
|||||||||||||||||||||
ющих возможные передаваемые полезные сигналы, и точкой, представляю- |
|||||||||||||||||||||
щей входную смесь сигнала и шума, эквивалентно определению факта попа- |
|||||||||||||||||||||
дания точки, представляющей смесь сигнала и шума, в область принятия того |
|||||||||||||||||||||
или иного решения. Нахождение точки, представляющей смесь сигнала и |
|||||||||||||||||||||
шума в области принятия конкретного решения, может быть реализовано пу- |
|||||||||||||||||||||
тем сравнения фазы вектора входной смеси и фазы несущего сигнала, пред- |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Р |
|
ставляющего конкретный информационный символ. Кроме того, из рисунка |
|||||||||||||||||||||
видно, что при демодуляции сигнала с M-PSK отсутствует необходимость |
|||||||||||||||||||||
амплитудного нормирования входной смеси сигнала и шума. |
И |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
|
|
|||
|
|
|
|
|
|
|
|
jy |
|
|
|
|
|
|
Вектор входной |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
смеси сигнала и |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Г |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
шума |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
/M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
к |
x |
- /M |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
Вект р |
|
|
|
Область |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
передаваем го |
|
правильного |
|
|
|
|
|
|
|
|
||||||||||
полезного с |
гнала |
т |
|
|
|
|
|
|
|
|
|
|
|||||||||
принятия решения |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 11.14. Геометрическая интерпретация принятия решения |
||||||||||||||||||||
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вероятность ошибки при приеме равновероятных информационных |
|||||||||||||||||||||
|
|
|
|
л |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
символов может |
ыть определена следующим образом: |
|
|
|
|
|
|
||||||||||||||
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
и |
c |
|
|
1 M |
|
|
|
|
/ M |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
Pe( k ) Pe( k ) 1 |
W( x )d( x ), |
|
|
|
(11.128) |
||||||||||||
Б |
Pe |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
M k 1 |
|
|
|
|
/ M |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где Pe( k ) – вероятность ошибочного приема k -го символа; W( x ) – плот- |
|||||||||||||||||||||
ность распределения вероятности разности фаз x входной смеси сигнала |
|||||||||||||||||||||
и помехи и присутствующего в ней полезного сигнала. |
|
|
|
|
|
|
|||||||||||||||
На основании вышеизложенного определим вероятность ошибки при |
|||||||||||||||||||||
приеме сигнала с M-PSK. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
211
|
|
|
X |
Q |
|
|
Поскольку фаза входного процесса |
|
|
|
|
, опре- |
|
X ( t ) равна x arctg |
X I |
|
||||
|
|
|
|
|
||
делим плотность распределения вероятности фазы через статистические ха-
рактеристики вектора X (t) .
Рассмотрим случай, когда фаза передаваемого сигнала S1(t) равна
1 0 . Для упрощения записи будем считать, что формирующий импульс имеет прямоугольную форму gF (t) 0, t 0, c и gF (t) 1, t 0, c . Сле-
довательно, вектор переданного сигнала на интервале k -го шага модуляции |
||||||
|
|
cos |
j sin |
A |
|
Р |
равен S A e j ( k ) |
E |
j0 . |
||||
0 |
c |
1 |
1 |
0 |
|
|
Здесь для получения общего энергетического соотношения используется ам- |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A2 |
|
|
|
плитудный множитель комплексной огибающей |
|
E |
|
|
|
|
0 |
|
c |
, учитываю- |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
щий энергетический параметр несущего колебания |
A0 |
|
и учитывается опера- |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Г |
|
|
|
|
||||||
ция интегрирования на интервале времени c . Вектор принимаемого сигнала |
|||||||||||||||||||||||||||||||||
имеет следующие компоненты: |
|
|
|
|
|
Б |
У |
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X I jXQ |
Ec nI jnQ . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
X |
|
а |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
к |
|
|
|
|
|
|
|
|
|
|
и nQ являются сов- |
||||||||
Поскольку квадратурные составляющие шума nI |
|||||||||||||||||||||||||||||||||
местно гауссовскими случайными величин ми с нулевыми средними, то |
|||||||||||||||||||||||||||||||||
квадратурные компоненты принима мого процесса X I |
и X Q тоже являются |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
вместная |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
совместно гауссовскими случайными в личинами со средними значениями |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
о |
е2 |
|
2 |
|
|
2 |
|
N0 |
|
|
|
|
|
|
|
||||||||||
X I |
|
Ec , XQ |
|
0 |
|
и дисперсиями I |
Q |
|
|
|
2 |
|
. |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Следовательно, |
с |
|
|
|
|
плотность |
распределения |
|
вероятности |
||||||||||||||||||||||||
квадратурных комп нент вх дного процесса будет равна |
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
л |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||
|
б |
и |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
1 |
|
|
X I Ec |
XQ |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
W ( X I , XQ ) |
|
|
|
exp |
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
(11.129) |
|||||||||
|
|
|
2 2 |
|
|
|
2 2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Используя правила преобразования статистических характеристик, |
|||||||||||||||||||||||||||||||||
можно |
|
перейти |
|
к |
|
|
плотности |
|
распределения |
|
|
вероятности модуля |
|||||||||||||||||||||
|
|
|
|
|
|
X |
Q |
|
|
|
|
X 2 |
X 2 |
||||
V |
|
|
и фазы вектора входного воздействия x arctg |
|
. |
|||
x |
|
|
||||||
|
|
I |
Q |
|
X I |
|||
|
|
|
|
|
||||
W (Vx , x ) Vr
2 2
|
V 2 |
E |
2 |
E V cos( |
) |
|
|||
|
x |
c |
|
|
c x |
x |
|
|
|
exp |
|
|
|
|
|
|
|
. |
(11.130) |
|
|
2 |
2 |
|
|
||||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
212

Проинтегрировав по области возможных значений модуля вектора входного воздействия [ 0, ), получим следующую плотность распределения
фазы вектора входного воздействия:
|
|
|
E |
|
sin2 ( x ) |
|
|
Ec |
|
2 |
|
|
|
1 |
2 |
|
c |
|
Vx 4 |
|
|
|
/ 2 |
|
|
|
N |
|
|
|||||||||
|
|
|
|
|||||||||
W( x ) W(Vx , x )dVx |
|
e |
N0 |
Vxe |
|
0 |
|
dVx . |
(11.131) |
|||
2 |
|
|
||||||||||
0 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
На рис. 11.15 изображены кривые плотности распределения вероятно- |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Р |
сти фазы вектора входного сигнала (плотности распределения вероятности |
||||||||||||
W ( x ), разности фаз x |
входной смеси сигнала и помехи и присутству- |
|||||||||||
ющего в ней полезного сигнала) для различных отношений Ec / N0 .
Как видно из рисунка, плотность распределения вероятности «концен- |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
||||||||
трируется» около истинного значения 1 0 по мере увеличения отношения |
|||||||||||||||||||||||
сигнал/шум Ec / N0 . |
|
|
|
|
|
|
|
Г |
|
И |
|||||||||||||
|
|
|
|
|
|
Б |
|
|
|
|
|
||||||||||||
W( x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
к |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
е |
а |
|
|
|
Ec |
|
6, дБ |
|
|
||||
|
|
|
|
Ec |
10, дБ |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
N0 |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
N0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
Ec |
3, дБ |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N0 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
л |
о |
|
|
|
|
|
|
|
|
Ec 0, дБ |
|
||||||||||
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
N0 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x, рад |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Рис. 11.15. Плотность распределения вероятности фазы вектора |
|||||||||||||||||||||||
Б |
|
|
|
|
|
|
|
входного воздействия |
|
|
|
|
|
|
|
|
|
|
|||||
Вероятность ошибочного приема символа находится в соответствии с приведенным выше выражением:
213

Pec 1 |
/ M |
|
/ M |
|
W( x )d( x ) 1 |
|
W( x )d( x ) , |
(1.132) |
|
|
/ M |
|
/ M |
|
а верхняя граница (все возможные ошибки при приеме информационного символа равновероятны) вероятности ошибочного приема конкретного элемента (бита) передаваемого сообщения будет определяться следующим образом:
|
|
Pb |
2k 1 |
|
Pc , k log ( M ). |
|
|
|
|
|
|
(11.133) |
||||||||
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
e |
|
|
2k 1 |
|
e |
|
2 |
|
|
|
|
|
|
|
Р |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
||||
На рис. 11.16 приведены зависимости вероятности ошибочного приема |
||||||||||||||||||||
передаваемых бит |
|
информации |
от отношения энергии, приходящейся на |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
|
|
|
|||
один передаваемый бит, к спектральной плотности мощности шума Eb / N0 |
||||||||||||||||||||
Pb |
|
|
|
|
|
|
|
|
|
|
|
|
Г |
|
|
|
|
|
||
для многопозиционной фазовой манипуляции. |
|
|
|
|
|
|
|
|
||||||||||||
e |
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
32-PSK |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
к |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
т |
8-PSK |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
о |
|
|
|
|
|
|
16-PSK |
|
|
|
||||||
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
л |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Б |
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Eb / N 0 , дБ |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 11.16. Вероятность ошибочного приема при многопозиционной |
||||||||||||||||||||
|
|
|
|
|
|
|
|
фазовой манипуляции |
|
|
|
|
|
|
|
|||||
В реальной |
ситуации |
при |
достаточно |
высоких отношениях Eb / N0 |
||||||||||||||||
наиболее вероятными являются ошибки, связанные с выбором соседних значений фазы i 1 и i 1 относительно фазы передаваемого сигнала i . В этом случае при использовании кода Грея для кодирования состояний фазыm данные ошибки приводят к искажению только одного из k элементов
214
(бит), определяющих передаваемый информационный символ, и вероятность ошибки конкретного бита может быть примерно оценена следующим образом:
Pb |
1 |
Pc , k log |
( M ). |
(11.134) |
|
|
|||||
e |
k e |
2 |
|
|
|
11.7.1.3. Квадратурная фазовая |
манипуляция и |
квадратурная |
|||
фазовая манипуляция со сдвигом (QPSK и OQPSK) |
|
||||
Квадратурная фазовая манипуляция и квадратурная фазовая манипуля-
ция со сдвигом являются частными случаями 4-позиционной фазовой мани- |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
||
пуляции. Это вид дискретной модуляции, при которой радиосигнал в общем |
||||||||||||||||||||||||||||||||||||||
виде может быть представлен следующим образом. |
|
|
|
|
|
|
Р |
|||||||||||||||||||||||||||||||
Сигнал с QPSK: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Г |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|||||
|
|
|
|
s( t ) |
|
|
|
|
|
g |
|
( t k ) |
|
|
C I cos t |
|
CQ sin t |
, |
(11.135) |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
F |
|
|
c |
|
|
k |
|
0 |
|
|
0 |
|
k |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
k |
0 |
|
|
|
|
|
|
|
k 0 |
|
|
|
|
|
|
|
|||||
сигнал с OQPSK: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
к |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k c )cos 0t 0 |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
A |
|
CkI gF ( t |
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
s( t ) |
|
k 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
(11.136) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
k |
|
g |
F |
( t ( k |
|
|
) |
c |
)sin t |
|
0 |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
0 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
ратурных |
|
несущ х колебаний; CkI |
1 и CkQ 1 – |
синфазная и квадратур- |
||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||
где A0 / |
|
|
2 , 0 , |
|
|
|
ьности |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
0 |
– амплитуда, центральная частота и начальная фаза квад- |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
л |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
ная последовате |
|
|
|
|
|
|
, соответствующие передаваемым информационным |
|||||||||||||||||||||||||||||||
|
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
символам «0» и «1» (обычно +1 соответствует «0», а–1 представляет «1»); |
||||||||||||||||||||||||||||||||||||||
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
gF ( t ) |
0 |
t 0, c – формирующий импульс; |
c |
– длительность символа |
||||||||||||||||||||||||||||||||||
модуляц |
|
; k – индекс текущего шага модуляции. |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
Б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пр мер временных функций, соответствующих радиосигналам с QPSK и OQPSK при прямоугольной форме формирующего импульса, приведен на рис. 11.17 и 11.18. На данных рисунках также приведены временные диаграммы, соответствующие основным компонентам рассматриваемых сигналов и поясняющие принцип их формирования.
Как видно из рисунков, исходный поток данных D( t ) разбивается на два параллельных потока, при этом синфазный поток DI ( t ) содержит условно нечетные биты исходного потока данных, а квадратурный DQ( t ) – условно четные. Длительность элементов синфазного и квадратурного потоков со-
215
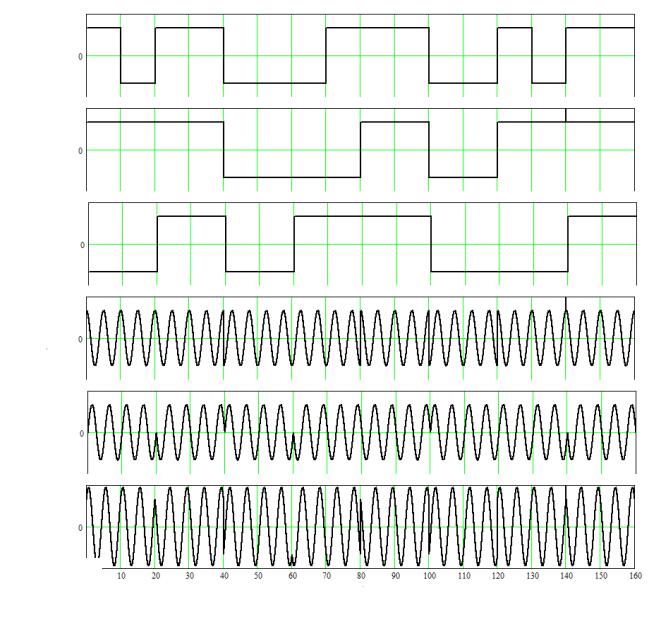
ответствует длительности символа модуляции c 2 b , равной удвоенной длительности информационного элемента (бита) исходного потока D( t ) . Результирующий радиосигнал получается путем суммирования квадратурных компонент, модулированных потоками DI ( t ) и DQ ( t ) , в соответствии с
/2-BPSK схемой модуляции.
Отличие метода модуляции OQPSK от QPSK заключается во временном сдвиге на b одного модулирующего потока, например DQ ( t ) , относи-
тельного другого. Данный сдвиг делает невозможным одновременную смену
состояний модулирующих потоков и, как следствие, исключает скачки фазы в результирующем радиосигнале на , что уменьшает паразитную амплитудную модуляцию и межсимвольные переходные искажения при прохождении радиосигнала через избирательные цепи.
|
|
|
|
|
|
|
|
|
|
|
|
|
Р |
D(t) |
1 |
2 3 4 5 |
6 |
7 8 |
9 10 |
11 12 13И14 15 16 |
|||||||
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
У |
|
|
|
|
|
|
|
|
|
|
|
|
Г |
|
|
DI(t) |
1 |
|
3 |
|
5 |
|
7 |
|
9 |
|
11 |
13 |
15 |
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
||
DQ(t) 2 |
|
4 |
|
6 |
|
к |
10 |
12 |
14 |
16 |
|||
|
|
|
|
|
|
8 |
|
|
|
||||
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
SI(t) |
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
SQ(t) |
|
л |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
S(t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
|
|
|
|
|
|
t
Рис. 11.17. Форма радиосигнала с QPSK:
D(t) – поток передаваемых данных;
216

DI(t) – синфазный поток передаваемых данных;
DQ(t) – квадратурный поток передаваемых данных;
SI(t) – синфазная компонента радиосигнала;
SQ(t) – квадратурная компонента радиосигнала;
S(t) – радиосигнал с QPSK
D(t) |
1 |
2 |
|
3 |
|
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
|
14 |
15 |
16 |
|
|
|
|
|
|||||||||||||||||
DI(t) |
|
1 |
|
|
3 |
5 |
|
|
7 |
9 |
|
|
11 |
|
13 |
|
15 |
Р |
||
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
|
DQ(t) |
|
|
2 |
|
|
4 |
|
6 |
|
|
8 |
10 |
|
12 |
|
14 |
16 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Г |
|
|
||
SI(t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
к |
|
|
|
|
|
|
|
|
|
SQ(t) |
|
|
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
||
S(t) |
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
л |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|||
|
|
Рис. 11.18. Форма радиосигнала с OQPSK: |
|
|
||||||||||||||||
и |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Б |
|
|
|
|
|
D(t) – поток передаваемых данных; |
|
|
|
|
||||||||||
|
|
|
DI(t) – синфазный поток передаваемых данных; |
|
|
|||||||||||||||
DQ(t) – квадратурный поток передаваемых данных;
SI(t) – синфазная компонента радиосигнала;
SQ(t) – квадратурная компонента радиосигнала;
S(t) – радиосигнал с QPSK
217
Комплексное представление радиосигналов с QPSK и OQPSK может быть определено следующим образом.
Для сигналов с QPSK:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
CkI gF ( t |
|
k b )cos 0t |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
sqpsk ( t ) |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Q |
|
|
|
|
|
|
( t k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
g |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
) sin t |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
F |
|
|
|
|
|
|
|
b |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
S qpsk ( t )cos t |
S qpsk |
( t ) sin t |
|
|
|
|
|
|
|
|
|
|
|
|
(11.137) |
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
I |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
Q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
И |
||||||||||
SIqpsk ( t ) |
|
A0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
gF ( t k b )CkI |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(11.138) |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 k 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
|
Р |
|||||||||||||||
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
||||||||||||||
SQqpsk ( t ) |
0 |
|
|
|
gF ( t k b )CkQ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Г |
|
|
|
|
(11.139) |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 k 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j t |
|
A |
|
|
|
|
|
I |
|
|
Q |
|
j t |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
sqpsk ( t ) SI ( t ) jSQ( t ) e |
|
|
|
|
|
|
|
|
|
|
|
|
gF ( t k b ) Ck |
jCk |
e |
|
(11.140) |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 k 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Для сигналов с OQPSK: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C I g |
|
( t k |
|
|
|
)cos t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F |
b |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
soqpsk ( t ) |
k 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
к |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
g |
|
|
( t ( k |
|
|
) |
)sin t |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
F |
|
|
е |
2 |
|
|
|
|
b |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
oqpsk |
|
|
|
|
|
и2 |
|
|
|
|
oqpsk |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
SI |
|
( t )cos 0t |
SQ |
|
|
|
|
( t )sin 0t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(11.141) |
|||||||||||||||||||||||||||||||||||||||
|
|
л |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
S oqpsk ( t ) |
A |
0 |
g |
|
|
|
( t k |
|
)C I |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(11.142) |
|||||||||||||||||||||||||||||||
I |
б |
|
|
|
|
|
|
|
|
|
k 0 |
|
|
F |
|
|
|
|
|
|
|
|
b |
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
oqpsk |
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
Q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
gF ( t ( k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
SQ |
|
( t ) |
|
|
0 |
|
|
|
|
|
) b )Ck |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(11.143) |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
Б |
|
|
|
|
|
|
|
|
|
2 k 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C I g |
|
( t k |
|
) |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
F |
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
||||||||
иs ( t ) S |
( t ) jS |
|
|
|
( t ) e j 0t |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( k 1 ) |
|
e j 0t |
. (11.144) |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
jCQ g ( t |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
oqpsk |
|
|
|
|
I |
|
|
|
|
|
|
|
|
|
|
|
|
Q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 k 0 |
|
) |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
F |
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|||||||
Комплексная огибающая сигнала полностью определяется его квадратурной и синфазной компонентами и представляется следующими выражениями:
218
|
|
|
|
( t ) |
A0 |
|
|
|
|
k |
) C I |
jCQ , |
|
|
|
|
|||||||
|
|
S |
qpsk |
g |
F |
( t |
|
|
|
(11.145) |
|||||||||||||
|
|
|
|
|
2 k 0 |
|
|
|
|
b |
k |
|
|
k |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
C I g |
F |
( t k ) |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
A0 |
|
k |
|
|
|
|
b |
|
|
|
|
|
|
|
|
|||
|
Soqpsk ( t ) |
|
|
jCQ g |
|
( t ( k |
1 ) |
|
. |
|
|
|
(11.146) |
||||||||||
|
|
|
|
|
|
2 k 0 |
|
F |
b |
) |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
2 |
|
|
|
|
|
||
Векторная диаграмма сигнала с квадратурной фазовой манипуляцией |
|||||||||||||||||||||||
представлена на рис.11.19. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
jy |
|
|
|
|
|
|
|
|
|
0t |
|
Р |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- /4 |
|
|
|
И |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
У |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Г |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
||
|
Рис. 11.19. Векторная диаграммак |
сигнала с QPSK/OQPSK |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
|
||||
Поскольку сигналы с QPSK и OQPSK по своей сути являются сигнала- |
|||||||||||||||||||||||
ми с 4-позиционной фаз в й манипуляцией, то при их демодуляции возмож- |
|||||||||||||||||||||||
но использование решающего правила, описанного выше в подразделе, по- |
|||||||||||||||||||||||
|
|
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
|
|||||
священном M-PSK мет ду м дуляции. |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Кроме этого, поскольку сигналы с QPSK и OQPSK являются линейной |
|||||||||||||||||||||||
комбинацией биортогональных сигналов с /2-BPSK, демодуляция может |
|||||||||||||||||||||||
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
осуществляться с параллельным использованием двух демодуляторов сигна- |
|||||||||||||||||||||||
|
|
л |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
лов с /2-BPSK со сдвинутыми на /2 опорными колебаниями. |
|
||||||||||||||||||||||
При демодуляции сигналов с BPSK особое внимание следует обратить |
|||||||||||||||||||||||
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
на точность восстановления опорного колебания. Для правильного принятия |
|||||||||||||||||||||||
решений |
|
демодуляции необходимо, чтобы фазовая ошибка восстановле- |
|||||||||||||||||||||
при |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ния опорного колебания стремилась к нулю ( t ) 0 (условие когерентной |
|||||||||||||||||||||||
Б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
демодуляции). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Нормированная корреляционная матрицы сигналов с QPSK и |
|||||||||||||||||||||||
OQPSK является сингулярной: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
219
|
1 |
0 |
1 |
0 |
|
|
|
|
|
|
|
|
0 |
1 |
0 |
1 |
|
|
1 |
0 |
1 |
0 |
. |
|
|
|
|
|
|
|
0 |
1 |
0 |
1 |
|
|
|
||||
Общее выражение для нахождения вероятности ошибки непосредственно применено быть не может. Но поскольку сигналы с QPSK и OQPSK являются линейной комбинацией биортогональных сигналов с /2-BPSK, то при параллельной демодуляции данных сигналов отсутствуют переходные помехи (взаимное влияние компонент с /2-BPSK друг на друга). При этом вероятность одновременно правильного приема в обоих каналах (вероятность
правильного приема |
|
символа, |
|
состоящего |
из |
2-х |
элементов |
C I 1 и |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
CQ 1) будет равна |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Р |
|||||||||||||||||||||
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
.У |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
1 |
|
|
|
|
Eb |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
Pc |
1 Pb bpsk |
|
|
|
|
1 |
erfc |
|
|
|
|
|
|
|
|
(11.147) |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
пр |
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
N0 |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Г |
|
|
|
|
|
|||||||
Соответственно |
|
вероятность |
|
|
|
|
иск жения 2-битового |
символа будет |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
определяться как Pc |
|
1 Pс . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
пр |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Вероятность ошибки при принятии |
|
онкретного бита равно вероятно- |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
к |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
сти принятия одного из трех возможных ошибочных решений (своеобразная |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
верхняя граница): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Pb |
|
22 1 |
|
|
Pc |
|
2 |
1 1 Pb bpsk 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
e |
|
|
|
2 |
2 |
1 |
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
b bpsk |
|
|
|
|
|
b bpsk |
|
2 |
|
|
2 |
|
|
|
b bpsk |
|
|
|
1 |
|
|
b bpsk |
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
1 1 2P |
|
|
|
|
|
|
|
|
|
|
2P |
|
|
|
1 |
|
|
|
P |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
P |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
e |
|
|
|
|
|
|
2 |
|
e |
|
|
|
|
(11.148) |
||||||||||||
|
3 |
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
4 1 |
|
|
|
|
|
E |
|
|
|
|
|
|
|
|
1 |
|
|
|
E |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
1 |
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
erfc |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
erfc |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
3 2 |
|
л |
|
|
|
|
|
4 |
|
|
|
|
N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
N |
0 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
E |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
2 |
|
|
|
|
E |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
erfc |
|
|
|
|
|
|
|
|
|
|
|
erfc |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Б |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
N0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
N0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
Если учесть, что вероятность возникновения ошибки сразу в двух каналах демодулятора значительно меньше вероятности ошибки только в одном канале, то вероятность ошибки конкретного бита примерно равна
220

|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
1 |
Eb |
|
|
1 |
Eb |
|
|
|
|||||
Pb |
Pc |
1 1 Pb bpsk |
|
erfc |
1 |
|
erfc |
|
|
, |
(11.149) |
||||||||
|
|
|
|
|
|
||||||||||||||
e |
|
e |
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|||
|
2 |
|
2 |
|
2 |
|
N0 |
|
|
4 |
|
N0 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
что практически совпадает с вероятностью ошибки при приеме сигнала с/2-BPSK (особенно при Eb / N0 1).
На рис. 11.20 приведены зависимости вероятности ошибки Peb и Pec при демодуляции сигналов с QPSK и OQPSK от отношения Eb / N0 , для
сравнения помехоустойчивости на рисунке приведена зависимость |
Pb |
при |
|
|
Р |
||
|
|
e |
|
демодуляции сигнала с /2-BPSK. |
И |
|
|
Необходимо отметить, что при одинаковых скорости модуляции и |
|||
мощности модулированного сигнала энергии, приходящиеся на один бит пе-
|
|
У |
редаваемой информации, для сигналов с /2-BPSK и QPSK совпадают. |
||
|
|
Г |
11.7.1.4. Явление обратной работы. Относительная (дифферен- |
||
циальная) фазовая манипуляция (DPSK, DQPSK) |
||
|
На |
|
Демодуляция сигналов PSK предполагает, что демодулятор располага- |
||
ет совершенной оценкой фазы несущей. |
|
пр Бктике фаза несущей, как пра- |
к |
|
|
вило, определяется по принятому сигн лу путем использования нелинейных |
||
е |
|
|
операций, которые приводят к неоднозначности фазы. Так при бинарной фа- |
||
зовой манипуляции сигнал часто подв ргается возведению в квадрат для снятия модуляции, затем образованный сигнал с удвоенной частотой фильтруется и делится по частоте на 2, для ого чтобы получить оценку частоты несу-
щей и фазы ( t ) . Эти операции приводят к неоднозначности фазы восста- |
|||||
новленного несущего к лебания на (180°). |
|||||
|
Аналогично |
|
|
т |
|
|
|
пр еме квадратурной фазовой манипуляции принима- |
|||
емый сигнал возвод тсяов четвертую степень, чтобы снять цифровую моду- |
|||||
|
|
|
при |
|
|
|
|
л |
|
|
|
ляцию, а затем четвѐртая гармоника частоты несущей фильтруется и делится |
|||||
|
б |
|
|
|
|
на 4 для того, что ы выделить компоненту несущей. Эти операции приводят |
|||||
к |
появлению |
компоненты с частотой несущей, содержащей оценку фазы не- |
|||
сущей ( t ) с точностью до постоянного слагаемого, равного ±90° или 180°. БАналог чные явления проявляются и при восстановлении несущего
колебания при приеме сигналов с многопозиционной фазовой манипуляцией. Следовательно, мы не имеем точной оценки фазы несущей в демодуляторе.
Подобные ошибки при восстановлении фазы несущего колебания приводят к ошибкам, проявляющимся в инверсии передаваемых символов на выходе демодулятора (двоичная «1» воспринимается как двоичный «0» и наоборот). Данное явление получило наименование «обратная работа». Опасность обратной работы заключается в том, что под действием помех может происходить неконтролируемый самопроизвольный перескок фазы восстановленного несущего колебания в пределах неоднозначности ее оцен-
221
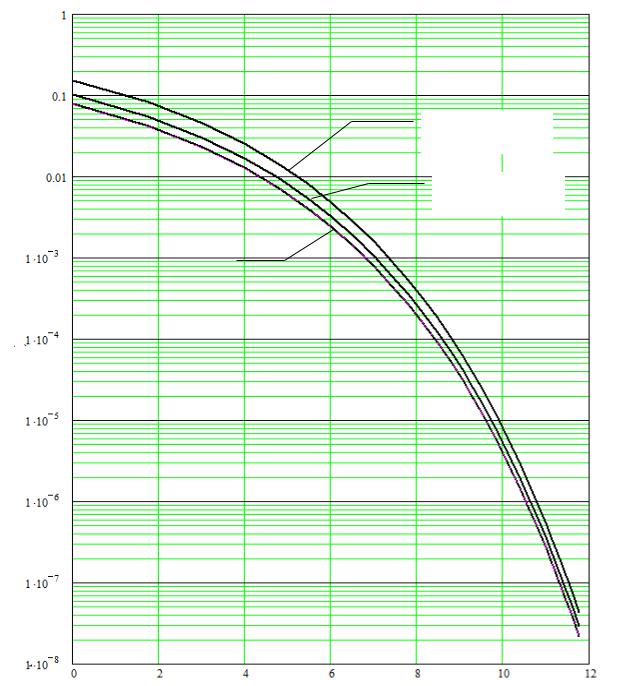
ки. Например, при приеме сигнала с /2-BPSK фаза восстановленного несущего колебания может произвольно перескакивать со значения ( t ) на
значение ( t ) и обратно, что является причиной неоднозначности восприятия демодулированных символов.
Pe
|
|
|
|
|
|
|
|
|
|
|
|
|
Р |
|
|
|
|
|
|
|
|
|
|
|
Pc |
И |
|
|
|
|
|
|
|
|
|
|
|
|
QPSK |
||
|
|
|
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
|
|
|
|
e |
|
|
|
|
|
|
|
|
Pb |
QPSK |
|
|
|
|
|
|
|
|
|
|
Г |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
Pb BPSK |
|
|
|
|
|
|
|
||||
|
|
|
|
|
а |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
к |
|
|
|
|
|
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
|
|
|
т |
|
|
|
|
|
|
||
|
|
|
|
о |
|
|
|
|
|
|
|
||
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
л |
|
|
|
|
|
|
|
|
|
|
|
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
|
|
|
|
|
Eb / N 0 , дБ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 11.20. Характеристики помехоустойчивости сигналов с QPSK и OQPSK
Проблема влияния неоднозначности фазы, возникающей при оценке фазы несущей ( t ) , обусловлена использованием так называемых методов
модуляции, использующих абсолютные значения фазы для кодирования пе-
222
редаваемых символов и может быть преодолена путѐм использования дифференциальной PSK (DPSK) вместо абсолютной PSK. При дифференциальной (относительной) фазовой манипуляции кодирование информации осуществляется посредством определения фазового набега (скачка) в зависимости от передаваемого символа на текущем шаге модуляции относительно предыдущего шага модуляции, а не самой абсолютной фазы, как при обычной PSK. Например, при бинарной PSK информационный символ «1» передаѐтся всегда с дополнительным сдвигом, равным , относительно преды-
дущего значения фазы (вне зависимости от значения предыдущего символа),
символ «0» передается без сдвига фазы, т.е. при передаче только одних «1» происходит непрерывное изменение фазы на от символа к символуР, напротив, при передаче одних «0» никаких скачков фазы сигнала при переходах от символа к символу происходить не будет.
Аналогично могут быть закодированы символы при передачи с использованием квадратурной фазовой манипуляции. Например, паре символов
«00» соответствует дополнительный скачок фазы относительно предыдущего |
||
Г |
И |
|
шага модуляции, равный 0; паре «01» – + /2; паре «10» – минус /2 и паре |
||
Б |
|
|
«11» – . Следует заметить, что приведенные схемы кодированияУ |
передавае- |
|
мой информации не являются окончательными и приведены только для ил- |
|
люстрации метода дифференциальной манипуляции. |
|
|
а |
Сигнал с дифференциально-кодиров нной фазовой манипуляцией |
|
к |
|
(DPSK) позволяет использовать демодуляцию, которая не требует оценки фа- |
|
е |
|
зы несущей. Вместо этого принимаемый сигн л на заданном сигнальном интервале (шаге модуляции) сравнива тся по фазе с принятым сигналом на
предыдущем сигнальном |
интервале |
. |
|
|||
|
|
|
||||
Рассмотрим подробнее общий случай многопозиционной дифференци- |
||||||
|
|
о |
|
|
||
альной фазовой манипуляции. В э ом случае радиосигнал в общем виде мо- |
||||||
жет быть представлен следующим образом: |
|
|||||
|
и |
|
|
|
||
л |
|
|
|
|
|
|
б |
s( t ) A0 |
gF ( t k c )cos( 0t k ) , |
(11.150) |
|||
|
|
|
k 0 |
|
|
|
|
|
|
|
|
|
|
k k 1 , |
|
|
|
|
|
|
где – скачок фазы, принимающий одно из возможных из М значений
m |
|
в |
соответствии с передаваемыми символами |
(обычно |
|
|
и2( m 1) |
|
|
||
m |
|
|
). На рис. 11.21 приведен пример временной функции, соот- |
||
|
|
||||
Б |
M |
|
|
||
ветствующей радиосигналу с DPSK для случая M 2 .
Комплексное представление радиосигналов с DPSK может быть записано следующим образом:
223
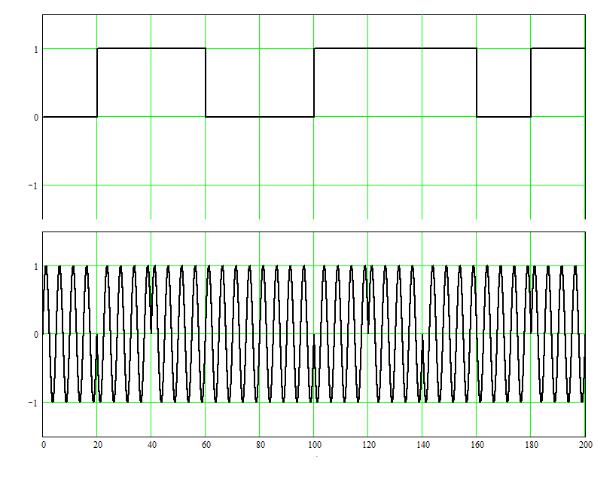
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s( t ) A0 |
g F ( t k c ) cos k cos 0t sin k sin 0t |
|
|||||||||||||||
|
|
k 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
SI ( t )cos 0t SQ( t )sin 0t |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(11.151) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
SI ( t ) A0 |
|
gF ( t k c )cos k |
|
|
|
|
|
|
(11.152) |
||||||||
|
|
|
k 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
SQ ( t ) A0 gF ( t k c ) sin k |
|
|
|
|
|
|
(11.153) |
||||||||||
|
|
|
|
k 0 |
|
|
|
|
|
|
|
|
|
|
|
Р |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
jSQ( t ))e |
j t |
|
|
|
|
|
|
|
|
j t |
|
|||
s( t ) ( SI ( t ) |
0 |
A0 gF ( t k c )(cos( k ) j sin( k ))e |
0 |
(11.154) |
|||||||||||||
|
|
|
|
|
|
|
|
|
k 0 |
|
|
|
|
|
И |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Г |
|
|
|
|
|
1 |
|
2 |
|
3 |
|
4 |
|
5 |
6 |
Б |
У8 9 |
|
10 |
|||
D(t) |
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
к |
|
|
|
|
|
|
|
|
1 |
|
2 |
|
3 |
|
4 |
е5 |
6 |
7 |
8 |
9 |
|
10 |
|||
|
10 |
|
|
10 |
|
о |
0 |
|
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
||||||
s(t) |
|
|
|
и |
т |
|
|
|
|
|
|
|
|
||||
|
л |
|
|
|
|
|
|
|
|
|
|||||||
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
Б |
|
|
|
|
Рис. 11.21. Форма сигнала с DBPSK (2-DPSK): |
|
|
||||||||||
|
|
|
|
|
|
|
|||||||||||
D(t) – поток передаваемых данных;
S(t) – радиосигнал с DBPSK
224
Комплексная огибающая сигнала представляется следующим выраже-
нием:
|
|
|
|
S( t ) A0 |
gF ( t k c )(cos( k ) j sin( k )) A0 |
gF ( t k c )e j k . |
(11.155) |
|
k 0 |
k 0 |
|
Как известно, оптимальный демодулятор осуществляет поиск максимальной из рассчитанных величин (значений функции или функционала правдоподобия):
|
|
|
1 |
c |
|
|
|
|
* |
|
|
Р |
||
P( X |
m ) exp |
|
|
X ( t ) S m( t ) X ( t ) S m( t ) |
dt |
. |
||||||||
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
N |
0 0 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
У |
Сложность вычисления функционала правдоподобия для случая сигна- |
|||||
лов с DPSK заключается в том, что на каждом шаге модуляцииИнесущие сиг- |
|||||
m |
( t ) представляют в общем случае разные передаваемые информаци- |
||||
налы S |
|||||
|
|
|
|
Б |
|
онные символы. Поиск максимального из |
M возможных значений функцио- |
||||
нала позволяет определить только факт наличия во Гвходной смеси сигнала и |
|||||
|
|
m |
|
|
l* |
шума конкретного несущего сигнала |
получена |
||||
S ( t ) , но никоим образом не позволяет |
|||||
|
к |
|
|
||
идентифицировать передаваемый символ. Информация о передаваемом ин- |
|||||
формационном символе может быть |
|
|
в результате сравнения иден- |
||
тифицированного несущего сигнала на предыдущем шаге модуляции Sk 1( t ) |
||||||||||||||||
|
|
|
|
|
|
|
т |
|
|
|
|
|
|
|||
с идентифицированным несущим сигналом на текущем шаге модуляции |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
Skm* ( t ) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Поскольку комплексная огибающая несущего сигнала на конкретном |
||||||||||||||||
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|||
шаге модуляции равна |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
л |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j |
|
j( |
k 1 |
) |
|
|
|
|
|
|
|
оk |
A0e |
|
|
|
, |
(11.56) |
||||||
|
б |
Sk ( t ) A0e |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
то для соседних шагов модуляции мы имеем |
|
|
|
|||||||||||||
и |
|
|
|
|
|
|
( t ) A e j k 1 |
; |
|
(11.157) |
||||||
|
|
|
|
|
|
|
S |
|
|
|||||||
Б |
|
|
|
|
|
|
|
k 1 |
|
0 |
|
|
|
|
|
|
|
|
|
S |
k |
( t ) A e j k A e j( k 1 ) . |
(11.158) |
||||||||||
|
|
|
|
|
|
|
|
0 |
|
0 |
|
|
|
|
||
Таким образом, идентификация переданного символа возможна на основе вычисления (определения) фазового запаздывания между идентифицированными на соседних шагах модуляции несущими сигналами:
* |
|
|
|
( t ) . |
|
|
m |
arg S* |
( t )S |
k |
(11.159) |
||
|
k |
1 |
|
|
||
225
Здесь, как и везде, символом * обозначается операция комплексного сопряжения для комплексных величин и функций ( Sk ) и оценка информаци-
онного параметра для скалярных величин.
Необходимо заметить, что правильность идентификации несущих сигналов (например, ошибочная идентификация за счет фазовой ошибки восстановления опорных колебаний при квадратурном преобразовании частоты) при использовании данного решающего правила не имеет существенного значения. Важно, чтобы данная ошибка была одинаковой для рассматриваемых двух соседних шагов модуляции.
Рассмотренное выше решающее правило определяет так называемый когерентный (синхронный) корреляционный прием, при котором используются синхронные копии всех возможных несущих сигналов, представляющих передаваемые информационные символы. В случае сигналов с DPSK
возможно использование более простого, так называемого автокорреляцион- |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Р |
ного решающего правила, являющегося квазикогерентным. |
|
|
|
|
||||||||||||||||||||||||||||
При автокорреляционном приеме в качестве опорного колебания ис- |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
|||
пользуется сама входная смесь полезного сигнала и шума. В этом случае |
||||||||||||||||||||||||||||||||
функционал правдоподобия записывается следующим образомУ: |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
Г |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
X k ( t ) |
X k 1( t |
c |
)e j m |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
N0 |
|
|
|
|
||||||||||||||||||||
|
|
P( X |
m ) |
exp |
|
|
|
0 |
|
|
|
|
|
Б |
|
|
|
|
, |
(11.160) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
( t ) |
|
|
( t |
|
|
|
* |
dt |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
X |
k |
X |
|
c |
)e j m |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k 1 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
к |
|
|
|
|
|
|
|
|
|
|
|
|
||||
где X k ( t ) – комплексная огибающая входной смеси сигнала и шума на те- |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
кущем шаге модуляции; Xk 1( t c |
) |
– задержанная на длительность символа |
||||||||||||||||||||||||||||||
модуляции |
|
комплексная |
|
|
гибающая входной смеси сигнала и шума на |
|||||||||||||||||||||||||||
предыдущем шаге м дуляции. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Преобразуем |
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
нтеграл, стоящий под знаком экспоненты. |
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
c |
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
* |
|
|
|
|
|||
|
X k ( t ) X k 1( t c |
)e j m X k ( t ) X k 1( t c |
)e j m |
dt |
|
|
||||||||||||||||||||||||||
0 |
|
|
л |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
)e j m dt . |
||||||
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( t |
|
||||||
бX ( t )X * |
( t ) X |
k 1 |
( t )X * |
1 |
( t ) 2 Re X |
k |
( t )X * |
1 |
c |
|||||||||||||||||||||||
|
|
|
k |
k |
|
|
|
|
|
|
k |
|
|
|
|
|
|
k |
|
|
|
|
|
|
||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Рассмотрим интегралы вида |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
|
|
|
* |
|
|
|
c |
|
|
|
|
|
m |
|
|
|
m |
|
* |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( t ) dt |
|
|
|
||||||||||
|
|
|
X k ( t )X k ( t )dt |
|
nk ( t ) Sk ( t ) nk ( t ) Sk |
|
|
|
||||||||||||||||||||||||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
|
|
|
* |
|
|
|
m |
|
m |
|
* |
|
|
|
|
|
m |
|
* |
dt |
|
|||||||
|
|
|
|
nk |
( t )nk ( t ) Sk |
|
( t )( Sk |
( t )) |
2 Re nk ( t )( Sk ( t )) |
|
||||||||||||||||||||||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
226

En Ec 0 , |
(11.161) |
где En – энергия реализации шума на интервале текущего шага модуляции; Ec – энергия, приходящаяся на один передаваемый информационный сим-
вол. Как видно, первые два слагаемых под знаком экспоненты в выражении для функционала правдоподобия на расположение максимума влияния не оказывают, поскольку не зависят от передаваемого символа. Следовательно, максимум функционала правдоподобия достигается при достижении максимума автокорреляционным интегралом и, соответственно, правило принятия решения о передаваемом информационном символе может быть сформулировано следующим образом:
зуется задержанная на длительность передаваемого символа копия входной
c |
|
|
*k 1( t c )e j m dt, |
|
|
|
Р(11.162) |
|
* m max |
|
Re X k ( t )X |
m 1,...,M . |
|||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
|
Полученное выше правило принятия решения соответствует алгоритму |
||||||||
|
|
|
|
|
|
У |
|
|
работы фазового детектора, у которого в качестве опорного сигнала исполь- |
||||||||
|
|
|
|
|
Г |
|
|
|
|
|
|
|
Б |
|
|
|
|
смеси сигнала и шума.
Рассмотрим автокорреляционный интегр л следующего вида:
|
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
* |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
X k ( t )X k 1( t |
c |
)dt |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
к |
l |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
* |
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
* |
|
|
|
|
|
|
||||||||
|
|
|
|
c n ( t )n |
( t ) S |
k |
( t )( S |
|
( t )) |
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
k |
|
k 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
k 1 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
е |
|
* |
|
|
|
m |
|
|
dt |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
* |
|
|
|
|
|
( t ) |
|
|
||||||||||||||||
|
|
|
|
0 |
n ( t )( S |
|
|
( t )) |
n |
|
( t )S |
k |
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
k |
|
|
|
|
k 1 |
|
|
|
|
|
|
|
k 1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
E e |
j( m l ) |
|
|
|
|
|
|
|
|
|
|
|
j( m n k 1 ) |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
E n |
|
e |
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
c |
|
|
|
|
т c |
k |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
j( |
|
n k |
) |
|
|
|
|
|
|
|
|
|
j( |
n k |
|
n k 1 |
) |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
оl |
|
|
|
|
|
nk nk 1e |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
Ec nk e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
иj( ) |
|
j n э |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(11.163) |
|||||||||
|
|
Ece |
|
|
|
|
|
nэe |
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
л |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
где nk |
nk 1 |
шумовые компоненты (случайные величины), отражающие эф- |
|||||||||||||||||||||||||||||||||||||
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
фект шумового воздействия на выходе коррелятора от реализаций шума на |
|||||||||||||||||||||||||||||||||||||||
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j n э |
– эквива- |
|
интервалах текущего и предыдущего шагов модуляции; n e |
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
э |
|
|
лентный шум на выходе коррелятора. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
Б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Из полученного выражения видно, что при достаточно больших отно-
шениях сигнал/шум фаза сигнала на выходе коррелятора (сигнал на выходе автокорреляционного фазового детектора) соответствует приращению фазы между несущими сигналами на соседних шагах модуляции, т.е. идентифицирует передаваемый информационный символ.
227

Точный расчет величины вероятности ошибки для приема сигналов с DPSK достаточно сложен, поэтому ограничимся рассмотрением случая достаточно больших отношений сигнал/шум. В этом случае можно пренебречь
шумовой компонентой n n e |
j( n k n k 1 ) |
ввиду ее малости по сравнению с |
||||||||||||||||||
|
|
|
|
|
|
|
|
k |
k 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j( l n k ) |
|
|
|
|
|
j( m n k 1 ) |
|
|||||||
компонентами |
|
E n e |
и |
|
E n |
e |
. Предположим, что |
|||||||||||||
|
|
c k |
|
|
|
|
|
|
|
|
c k |
1 |
|
|
|
|
||||
передавался |
символ, |
|
кодированный |
нулевым приращением фазы |
||||||||||||||||
m 0 , тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
1 |
|
c |
|
|
* |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
X k ( t )X k |
1( t c )dt |
Ec nk 1 nk . |
|||||||||
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
Ec |
|||||||||||||||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Шумовые компоненты |
nk 1 |
и nk являются гауссовскими иРнекоррели- |
||||||||||||||||||
рованными (вообще, статистически независимыми). Определим действитель- |
||||||
|
|
|
|
Г |
И |
|
ную и мнимую части автокорреляционного интеграла |
|
|||||
|
|
|
|
Б |
У |
|
x |
|
|
|
|
||
Ec Re nk 1 |
nk , |
y Im nk 1 nk . |
||||
|
|
|
а |
|
|
|
Случайные величины x и y , ввиду линейности определяющих их опе- |
||||||
|
|
к |
|
|
|
|
раций и свойств комплексного предст вления белого гауссовского шума яв- |
||||||
ляются гауссовскими и независимыми друг от друга. Дисперсия случайных |
|||||||||
|
|
|
е |
|
|
|
|
||
величин x и |
y равна удвоенной дисп рсии синфазной и квадратурной ком- |
||||||||
|
|
т |
|
|
|
N0 |
|
|
|
понент 2x 2y 2 |
2 n2 |
2 n2 |
2 n2 |
2 |
|
N0 |
исходных случайных |
||
|
|
I |
|
Q |
|
2 |
|
|
|
|
|
о |
|
|
|
|
|
|
|
величин nk 1 |
и nk . |
|
|
|
|
|
|
|
|
Фаза автокорреляци нн го интеграла (оценка приращения фазы за счет |
|||||||||
передаваемого на текущем шаге информационного символа) будет равна |
|||||
|
|
|
л |
||
* |
|
y |
|
и |
|
|
arctg |
|
. |
||
|
|||||
|
|
б |
|||
|
|
x |
|
||
|
Далее применима методология нахождения вероятности ошибки, опи- |
||||
|
и |
|
|
|
|
санная ранее при рассмотрении качественных характеристик демодуляции |
|||||
Б |
|
|
|
|
|
сигналов с M-PSK. Отличие итогового результата для демодуляции сигналов DPSK заключается в удвоенной мощности (дисперсии) шума. Следовательно, прием сигналов с DQPSK обеспечивает такую же вероятность ошибки, как и прием сигналов с PSK одинаковой размерности, при условии увеличения отношения сигнал/шум в два раза (на 3 дБ). Данное утверждение достаточно справедливо для размерности модуляции M 4 . Для случая бинарной дифференциальной фазовой манипуляции данная оценка вероятности ошибочного приема является слишком пессимистической. Для сигналов с бинарной манипуляцией (DBPSK) применимо следующее соотношение для вероятности ошибочного приема:
228
|
1 |
e |
Eb |
|
||
Pb |
N0 |
. |
(11.164) |
|||
|
||||||
e |
2 |
|
|
|
|
|
|
|
|
|
|
||
11.7.2. Частотная манипуляция (FSK)
11.7.2.1.Бинарная частотная манипуляция (BFSK)
|
Р |
Бинарная частотная манипуляция (просто частотная манипуляция) – вид дискретной модуляции, при которой радиосигнал в общем виде может
быть представлен следующим образом: |
|
|
|
|
И |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
s( t ) A0 |
gF ( t k b )cos ( 0 Ck |
d )t 0 |
, |
|
|
(11.165) |
||||||||||
|
|
|
|
|
|
|
k 0 |
|
|
|
|
Г |
|
|
|
|
|
||
где A , |
, |
|
|
|
|
|
|
|
|
|
Б F |
|
|
|
b |
|
|||
0 |
0 |
|
0 |
|
|
|
|
|
|
|
|
У |
|
|
|
|
|||
колебания; d |
– принятая девиация частоты; Ck 1 – последовательность, |
||||||||||||||||||
соответствующая передаваемым информационным символам |
«0» и |
«1» |
|||||||||||||||||
(обычно +1 соответствует «0», а–1 предст вляет «1»); g |
|
( t ) 0 |
t 0, |
|
– |
||||||||||||||
формирующий импульс; b – |
|
к |
|
|
|
|
|
|
|
|
|
||||||||
длительность информационного символа (би- |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
|
|
та); k – текущий номер передава мого информационногоа |
символа. |
|
|
|
|||||||||||||||
Формирующий импульс в общ м случае может иметь произвольную |
|||||||||||||||||||
|
|
|
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
|
форму gF ( t ). Чаще всего использу тся прямоугольная форма импульса. |
|
|
|||||||||||||||||
Примеры временных функций, соответствующих радиосигналу с BFSK |
|||||||||||||||||||
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
||
при прямоугольной |
|
ф рме |
формирующего |
импульса, приведен |
|
на |
|||||||||||||
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
||
рис. 11.22 и 11.23. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
л |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
229
D(t)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Р |
s(t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ла |
Г |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|||
|
|
Рис. 11.22. Форма радиосигн |
Бс BFSK (общий случай) |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
к |
|
|
|
|
|
Комплексное представление радиосигнала с BFSK может быть опреде- |
|||||||||||||||||
лено следующим образом: |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
т |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
еjC |
t |
j t |
|
|
|
|||
|
|
|
|
о |
|
( t k )e k |
d e |
0 . |
|
(11.166) |
|||||||
|
|
|
s( t ) A |
g |
F |
|
|||||||||||
|
|
|
|
0 |
k 0 |
|
|
|
|
b |
|
|
|
|
|
||
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Комплексная |
г бающая сигнала с бинарной частотной манипуляцией |
||||||||||||||||
|
|
л |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
представляется с едующ м выражением: |
|
|
|
|
|
||||||||||||
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k )e jCk d t |
|
|
|
|
||||
и |
S( t ) |
A g ( t |
|
|
|
|
|||||||||||
|
|
|
|
0 |
|
F |
|
|
|
|
b |
|
|
|
|
|
|
Б |
|
|
|
k 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A0 gF ( t k b ) cos( d t ) j sin( Ck d t ) . |
|
(11.167) |
||||||||||||
|
|
|
k 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Синфазная и квадратурная компоненты комплексной огибающей опре- |
|||||||||||||||||
деляются следующим образом: |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
SI ( t ) |
A0 gF ( t k c )cos d t ; |
|
(11.168) |
|||||||||||
|
|
|
|
|
|
k 0 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
SQ ( t ) A0 |
gF ( t k c )Ck sin d t . |
|
|
(11.169) |
|||||||||||
|
|
|
|
|
k 0 |
|
|
|
|
|
|
|
|
|
|
|
|
230 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

D(t)
|
|
|
|
|
|
|
|
|
|
|
Р |
|
|
|
|
|
|
|
|
|
|
|
И |
|
|
s(t) |
|
|
|
|
|
|
|
У |
|
|
||
|
|
|
|
|
|
|
|
Г |
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
|
|
|
|
|
к |
|
|
|
|
t |
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
Рис.11.23. Форма радиосигнала с BFSK (без разрыва фазы) |
|
||||||||||
ся на передачу нф рмац ивторая, |
половина энергии не несет информаци- |
|||||||||||
Анализ соотношений для квадратурной и синфазной компонент сигна- |
||||||||||||
|
|
|
того |
|
|
|
|
|
|
|
|
|
ла с бинарной частотной манипуляцией показывает, что только половина |
||||||||||||
энергии |
Ec Eb , прих дящейся на один символ (бит) модуляции, расходует- |
|||||||||||
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
л |
|
, метод наложения информационной составляю- |
|||||||||
онной нагрузки. Кроме |
||||||||||||
щей на сигнал-нос те ь соответствует методу /2-BPSK квадратурной со- |
||||||||||||
|
б |
|
|
|
|
|
|
|
|
|
|
|
ставляющей радиосигнала. Изложенное выше позволяет предположить, что |
||||||||||||
и |
|
|
|
|
|
|
|
|
|
|
|
|
помехоустойчивость демодуляции сигнала с BFSK будет проигрывать 3 дБ |
||||||||||||
помехоустойч вости демодуляции сигналов с /2-BPSK (данное предполо- |
||||||||||||
Б |
|
|
|
|
|
|
|
|
|
|
|
|
жен е будет подтверждено ниже).
Векторная диаграмма сигнала с бинарной частотной манипуляцией представлена на рис. 11.24.
231

jy |
± dt |
0t |
|
x
|
|
|
Р |
|
|
И |
|
|
У |
|
|
Рис. 11.24. Векторная диаграмма сигнала с BFSK |
|||
Г |
|
|
|
При квазиоптимальном приеме решение принимается на основании |
|||
Б |
|
|
|
наблюдения входной смеси сигнала и шума на интервале времени, соответствующем длительности b , с учетом этого для интервала наблюдения на k -
м интервале модуляции комплексная огибающая может быть переписана в следующем виде:
|
|
|
|
|
|
|
|
|
|
|
( t k |
|
)e jCk d t |
|
|
|
||||||
|
|
|
|
|
|
S( t ) A g |
F |
b |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
а |
sin( t ) , |
|
|||||
|
|
|
|
|
|
A g |
F |
( t k |
b |
) cos( |
t ) jC |
(11.170) |
||||||||||
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
d |
|
k |
d |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
к |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
||||
а соответствующий ей радиосигнал будет определяться следующим образом: |
||||||||||||||||||||||
s( t ) A0 gF ( t k b ) cos( d t )cos( 0t ) Ck sin( d t )sin( 0t ) |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
||||
|
A0 gF ( t k b о)cos ( 0 |
d )t , Ck |
1 |
|
|
|||||||||||||||||
|
A g |
F |
( t иk )cos ( |
|
|
)t , C |
k |
1 |
|
. (11.171) |
||||||||||||
|
0 |
|
|
b |
|
0 |
|
|
d |
|
|
|
|
|
|
|
|
|||||
A g |
F |
|
(лt k |
)cos ( |
C |
|
d |
)t |
|
|
|
|
|
|
||||||||
|
0 |
|
|
|
b |
|
|
0 |
|
|
k |
|
|
|
|
|
|
|
|
|
||
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Таким |
|
образом, сигнал, несущий информацию о передаче двоичной |
||||||||||||||||||||
«1», можно записать как |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Б |
|
|
|
s1( t ) A0 gF ( t k b ) cos(( 0 |
d )t ) , |
(11.172) |
||||||||||||||||
и сигнал, несущий информацию о передаче двоичного «0», |
|
|||||||||||||||||||||
|
|
|
|
|
s0( t ) A0 gF ( t k b ) cos(( 0 |
d )t ) . |
(11.173) |
|||||||||||||||
232 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

Функционал правдоподобия, соответствующий передаче двоичной «1»,
|
|
|
|
|
|
1 |
b |
|
|
|
|
|
|
|
* |
|
|
|
|
||
P( X |
1) exp |
|
|
X ( t ) S1( t ) X ( t ) |
S1( t ) |
dt |
|
|
|
||||||||||||
N0 |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
1 |
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
X ( t ) A g |
|
( t |
k |
) cos( |
t ) j sin( |
t ) |
|
||||||||||
|
|
|
F |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
0 |
|
|
b |
d |
|
|
d |
|
|
|
|||
exp |
|
|
N0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(11.174) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
* |
|
|
|
|
|
X ( t ) A g |
|
( t k |
|
|
|
|
|
|
|
||||||||||
|
|
F |
b |
) cos( t ) j sin( t ) dt |
|
|
|||||||||||||||
|
|
|
|
|
|
|
0 |
|
|
|
|
|
d |
|
d |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
|
|
и передаче двоичного «0» |
|
|
|
|
|
|
У |
Р |
|||||||||||||
|
|
|
|
|
|
1 |
|
b |
|
|
|
|
|
|
* |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
P( X |
0 ) |
exp |
|
|
|
X ( t ) S |
0( t ) X ( t ) S |
0( t ) |
dt |
|
|
|
|
|||||||||
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
0 |
|
0 |
|
|
|
|
|
|
|
|
Г |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
1 |
b |
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
X ( t ) A0 gF ( t k b ) cos( d t ) j sin( d t ) |
|
|
|||||||||||||||||
exp |
|
N0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
(11.175) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
* |
|
|
|
|
|
|
X ( t ) A g |
|
( t k |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
F |
b |
) cos( t ) j sin( t ) dt |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
0 |
|
|
|
|
d |
|
|
d |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
е |
|
|
смеси полезного сигнала |
||||||
где X ( t ) – комплексная огибающая входнойа |
||||||||||||||||||||||
и шума. |
|
|
|
|
|
|
|
|
т |
к |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Решение о значении пер дава мого информационного символа Ck на |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
формируе |
|
|
|
|
|
|
|
|
|
|||
k-м шаге модуляции |
|
|
ся на основании сравнения рассчитанных |
|||||||||||||||||||
значений |
функционала |
(функции |
|
для дискретного времени |
наблюдения) |
||||||||||||||||
правдоподобия. |
|
и |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
л |
|
|
0 ) P( X |
|
1) C* 1 |
|
|
|||||||||||||
|
|
|
|
|
|
||||||||||||||||
|
б |
|
P( X |
|
(передавался "0") ; |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
C* 1 |
|
|
||||||
|
|
|
|
|
P( X |
0 ) P( X |
1) |
(передавалась "1") |
|||||||||||||
ли P X |
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ln |
|
|
|
|
|
|
0 C*k |
1 |
( передавалась "1") ; |
(11.176) |
||||||||||
|
|
|
|
|
|
||||||||||||||||
|
|
P X |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P X |
|
0 |
C*k |
1 |
|
|
|
|
||||||||||||
|
ln |
|
|
|
|
|
|
|
|
( передавался "0") . |
(11.177) |
||||||||||
|
|
|
|
|
|
|
|||||||||||||||
|
|
P X |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В итоге, осуществив необходимые преобразования, имеем:
233
b |
C*k |
|
|
|
|
|
XQ ( t ) sin( d t ) 0 |
1 |
( передавалась "1") , |
(11.178) |
|
0 |
|
|
|
|
|
b |
C*k |
|
|
|
|
|
XQ ( t ) sin( d t ) 0 |
1 |
( передавался "0") , |
(11.179) |
|
0 |
|
|
|
|
|
где XQ( t ) – квадратурная компонента комплексной огибающей входной
смеси сигнала и помехи.
Таким образом, в процессе демодуляции сигнала с BFSK участвует
|
Р |
только одна из двух квадратурных компонент, вторая, не несущая информа- |
|
ционной нагрузки, демодулятором игнорируется. |
И |
Наличие в полезном сигнале составляющей синхронной с несущей частотой и девиацией частоты позволяет осуществлять некогерентный прием
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
XГI(t) |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
Х |
|
|
|
|
|
ФНЧ |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
cos( 0t+ (t)) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
x(t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
к |
|
|
|
ФД |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
ФНЧ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
Х |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
XQ(t) |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
и |
|
|
|
-sin( 0t+ (t)) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
л |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Р с. 11.25. Автокорреляционный демодулятор сигнала с BFSK |
||||||||||||||||||||||||||||||||||
|
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Необходимо отметить, что некогерентный прием проигрывает в поме- |
|||||||||||||||||||||||||||||||||||
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
при малых отношениях сиг- |
||||||||||||||||||
хоустойчивости когерентному (особенно |
||||||||||||||||||||||||||||||||||||
нал/шум). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Определим элементы нормированной корреляционной матрицы сиг- |
|||||||||||||||||||||||||||||||||||
нала с BFSK. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
km |
1 |
|
b sk ( t )sm( t )dt |
1 |
|
b sk ( t )sm( t )dt . |
(11.180) |
||||||||||||||||||||||||
|
|
|
|
|
E |
|
E |
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
сигналов с BFSK, слабо чувствительный к ошибке восстановления опорного колебания квадратурного преобразователя частоты. Схема некогерентного «автокорреляционного» демодулятора приведена на рис. 11.25.
234

При прямоугольной форме формирующего импульса имеем
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
22 |
|
|
1 |
|
|
b A0 cos ( 0 d )t 2 dt |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
E |
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
A2 |
b |
|
1 , |
|
|
|
|
|
|
|
|
|
|
|
|
(11.181) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
Eb |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
где E |
A2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
0 b |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
b |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
1 |
b A |
|
cos ( |
|
|
|
|
)t |
|
У |
Р |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
12 |
|
|
|
|
|
|
21 |
|
|
|
|
Eb |
|
0 |
|
|
|
|
0 |
|
d |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Г |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
A0 cos ( 0 d )t dt |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
1 |
|
|
|
2 b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
A0 |
|
cos( 2 |
d |
|
|
|
|
0 |
|
|
|
|||||||||||||||||||||||||
|
Eb |
2 |
|
|
|
|
|
|
t ) cos( 2 |
t ) dt |
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
к |
|
|
Б |
|
|
(11.182) |
||||||
|
|
1 |
|
|
|
|
A0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
sin( 2 d b ) |
1 |
|
|
|
sin( 2 d b ) ; |
|
|||||||||||||||||||||
|
Eb 2 |
|
|
|
|
|
|
|
|
|
2 d |
b |
|
||||||||||||||||||||||||||
|
|
2 d |
|
|
|
|
|
|
|
|
е |
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
b |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
т |
|
|
1 |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
2 |
|
sin( 2 d b ) |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
. |
|
(11.183) |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin( 2 d b ) |
|
|
|
|
1 |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
л |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Вероятность |
ош бочного приема информационного |
символа (бита) |
|||||||||||||||||||||||||||||||||||||
можно опреде ить на основании общего выражения для ошибки приема, полученного ранее:
|
б1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
b |
|
|
u1 2Eb / N0 (1 12 ) |
|
|
1 |
|
|
T |
|
1 |
|
||||||
Pe |
1 |
|
|
|
( |
|
|
exp |
|
u |
|
ρ |
u du2 )du1 . |
(11.184) |
||||
( 2 ) |
|
|
|
|
||||||||||||||
и |
ρ |
1 / 2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
||||
БНаиболее |
интересным с точки зрения практического использования яв- |
|||||||||||||||||
ляется ортогональная FSK, для которой ij |
0 |
i |
|
j |
, в этом случае |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
235
|
|
|
|
|
|
|
|
|
F( x |
|
dx |
|
|
|
|
|
|
|
b |
|
1 |
|
x |
2 |
/ 2 |
|
1 |
|
Eb |
|
|
||||||
1 |
|
e |
|
|
|
|
|
|
||||||||||
Pe |
|
|
|
|
|
|
2Ec / N0 |
|
erfc |
|
|
. |
(11.185) |
|||||
|
|
|
|
|
|
|
2N0 |
|||||||||||
|
|
|
|
|
|
|||||||||||||
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
||||
Сравнивая |
полученное выражение с выражением |
для вероятности |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
E |
|
||
ошибки приема |
сигнала с /2-BPSK (рис. 11.11) Pb |
|
|
|
erfc |
b |
|
|
|
|
|
|
|||||||
|
e BPSK |
|
2 |
|
N0 |
|
|
||
|
|
|
|
|
|
|
|||
необходимо отметить, что метод BFSK модуляции проигрывает в помехоустойчивости методу /2-BPSK ровно 3дБ.
В случае некогерентного приема вероятность ошибочного приема может быть оценена следующим образом:
|
|
|
|
|
|
|
1 |
|
|
Eb |
|
|
|
|
Р |
||
|
|
|
b |
|
|
2 N0 |
|
|
|
|
|||||||
|
|
|
Pe |
|
|
2 |
e |
|
|
. |
|
|
|
И |
(11.186) |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
На рис. 11.26 приведены зависимости вероятности ошибки от отноше- |
|||||||||||||||||
ния сигнал/шум для когерентного и некогерентного приемаУсигналов с орто- |
|||||||||||||||||
гональной BFSK, для сравнения там же приведена зависимость вероятности |
|||||||||||||||||
ошибки для приема сигнала с /2-BPSK. |
|
|
Г |
|
|
||||||||||||
|
|
|
|
|
|
||||||||||||
Ортогональная BFSK |
|
реализуется |
|
при |
выполнении условия |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
sin( 2 d b ) 0, отсюда вытекают требов ния к девиации частоты: |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
||
|
|
2 d b |
4 fd b n, |
|
n 1, 2,... , |
|
|
||||||||||
|
|
|
|
|
|
|
к |
|
|
|
|
|
|||||
f |
|
|
n |
|
|
n |
C, |
|
n 1, 2,... , |
|
|
(11.187) |
|||||
d |
|
|
|
|
|
|
|||||||||||
|
|
|
е |
|
|
|
|
|
|
|
|||||||
|
|
|
4 b |
|
4 |
|
|
|
|
|
|
|
|
|
|
||
где C – скорость м дуляции (манипуляции) [бит/c]. При больших девиациях |
||||||
|
|
|
т |
|
|
|
частоты (малых отношениях Td / b , Td 1/ fd ) |
квазиортогональность дости- |
|||||
|
|
о |
|
|
|
|
гается автоматически за счет множителя |
1 |
|
, входящего в коэффициенты |
|||
|
|
|||||
|
|
|||||
|
|
и |
|
2 d |
b |
|
взаимной корреляциил. |
|
|
||||
|
|
|
|
|||
|
б |
|
|
|
|
|
11.7.2.2. М-позиционная (многопозиционная) |
||||||
и |
|
|
|
|
|
|
частотная манипуляция (M-FSK) |
|
|
|
|||
Б |
|
|
|
|
|
|
М-позиционная (многопозиционная) частотная манипуляция – вид дискретной модуляции, при которой радиосигнал в общем виде может быть
представлен следующим образом:
|
d ( t ))t 0 , |
|
s( t ) A0 gF ( t k c )cos ( 0 |
(11.188) |
|
k 0 |
|
|
236
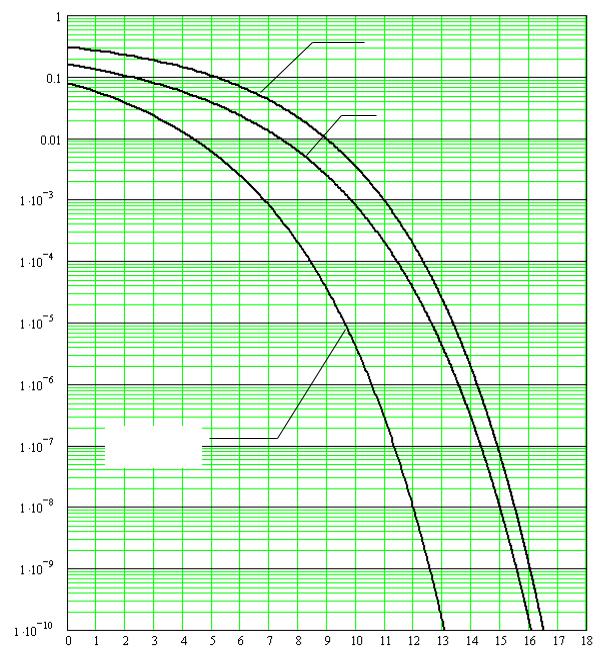
где A0 , 0 , 0 – амплитуда, центральная частота и начальная фаза несущего колебания; d ( t ) – девиация частоты, соответствующая передаваемой информации; gF ( t ) 0 t 0, c – формирующий импульс; c – длительность информационного символа; k – текущий номер передаваемого информационного символа. Девиация частоты d ( t ) постоянна на интервале времени, совпадающем с интервалом действия информационного символа и принимает одно из M известных значений d m .
Pb |
|
|
|
|
|
|
|
|
|
|
|
|
Р |
|||
e |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
BFSK |
И |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
некогерентный прием |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
BFSK |
У |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Г |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
когерентный прием |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
к |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-BPSK |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
л |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
|
|
|
|
Eb / N 0 |
, |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
дБ
Рис. 11.26. Вероятность ошибки при приеме сигналов с BFSK
237
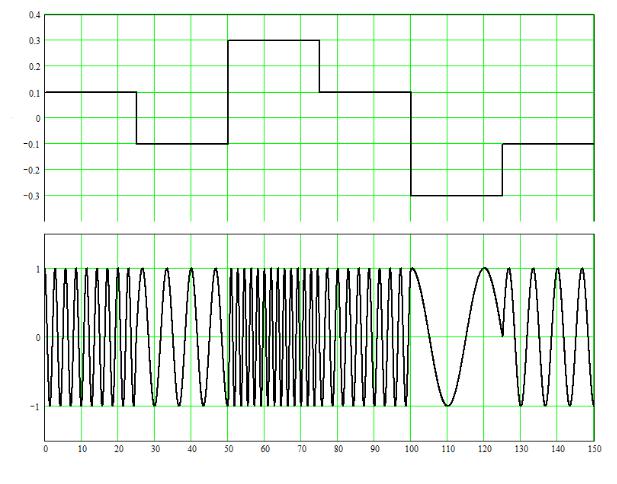
Пример временной функции, соответствующей радиосигналу 4-FSK при прямоугольной форме формирующего импульса, приведен на рис. 11.27.
|
|
01 |
11 |
|
|
|
|
|
|
00 |
|
01 |
|
|
|
10 |
|
11 |
|
d(t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Р |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Г |
|
|
|||
s(t) |
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
к |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
d |
|
|
||||
|
|
|
|
т |
|
|
|
|
|
|
|
|
t |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 11.27. Форма радиосигнала с 4-FSK |
|
|
||||||||||||||
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
На рисунке введены следующие обозначения: ( t ) – девиация часто- |
|||||||||||||||||||
|
|
л |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ты, соответствующаяопередаваемой информации; S(t) – радиосигнал с BFSK. |
|||||||||||||||||||
Комп ексное представление радиосигнала с BFSK может быть опреде- |
|||||||||||||||||||
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
лено следующим образом: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
и |
|
|
A |
|
|
|
( t k )e |
j d m t |
e |
j |
t |
. |
|
|
(11.189) |
||||
Б |
|
|
s( t ) |
g |
|
|
|
0 |
|
|
|
||||||||
|
|
|
|
0 |
k 0 |
F |
|
|
c |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Комплексная огибающая сигнала с бинарной частотной манипуляцией |
|||||||||||||||||||
представляется следующим выражением: |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
( t k |
|
|
)e jC d m t |
|
|
|
|
|
|
|
|
|||
|
|
S( t ) A g |
F |
c |
|
|
|
|
|
|
|
||||||||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
k 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(11.190) |
|
|
|
|
|
|
|
|
|
|
|
|
j sin( d m t ) . |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
A0 |
gF ( t k c ) cos( d m t ) |
|
|
||||||||||||||
|
|
|
k 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
238
При квазиоптимальном приеме решение принимается на основании наблюдения входной смеси сигнала и шума на интервале времени, соответствующем длительности информационного символа c , для интервала
наблюдения на k-м интервале модуляции комплексная огибающая может быть переписана в следующем виде:
|
|
( t k |
)e j d m t . |
(11.191) |
S( t ) A g |
F |
|||
0 |
b |
|
|
|
Решение о значении передаваемого информационного символа (значе- |
||||
нии девиации частоты d m ) на k-м шаге модуляции формируется на основа-
нии сравнения рассчитанных значений функционала правдоподобия и опре- |
|||||||||||||||
деления того значения параметра m , которое обеспечивает его максимум. |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Р |
|
|
|
|
|
1 |
c |
|
|
|
|
* |
|
|
|
|
|
|
|
|
|
И |
|
||||||||||
P( X |
m ) exp |
|
|
|
|
X ( t ) S m( t ) X ( t ) S m( t ) |
dt |
|
. |
|
(11.192) |
||||
|
|
||||||||||||||
|
|
|
|
N0 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
|
|
|
||
|
|
|
|
|
|
|
|
|
Г |
|
|
|
|
|
|
Как уже неоднократно отмечалось, для симметричных каналов поиск |
|||||||||||||||
максимума функционала правдоподобия соответствует поиску максимума |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
среди корреляционных интегралов следующего вида: |
|
||||||||||||||||||||
|
|
c |
|
|
|
m |
* |
|
|
|
|
|
|
|
а |
|
|||||
|
|
|
|
|
|
( t ) |
|
|
|
|
|
|
к |
|
|
||||||
|
Re |
X ( t ) S |
|
|
dt |
. |
|
|
|
|
|||||||||||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
е |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Поскольку функции |
m |
|
|
|
|
|
||||||||||||||
|
S |
|
|
|
|
|
|
||||||||||||||
|
|
( t ) |
представляют гармонические колебания с |
||||||||||||||||||
известной частотой d m |
|
|
и фазой, значения данных корреляционных инте- |
||||||||||||||||||
гралов соответствуют ткликамтсинхронных детекторов с опорными колеба- |
|||||||||||||||||||||
ниями вида cos ( |
|
|
)t при когерентном детектировании или откликам |
||||||||||||||||||
|
|
|
|
|
|
0 |
|
оd m |
|
|
|
|
|
|
|
|
|||||
обычных амп итудных детекторов, |
стоящих на выходе полосовых фильтров |
||||||||||||||||||||
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|||
настроенных на частоты |
0 d m при некогерентном детектировании. |
||||||||||||||||||||
|
Определимлвероятность ошибочного приема для сигнала с M-FSK при |
||||||||||||||||||||
услов |
|
ортогональности |
несущих |
различные информационные |
символы |
||||||||||||||||
|
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
сигналов (достаточно большом разносе между частотами d m ). В этом слу- |
|||||||||||||||||||||
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
чае нормированная корреляционная матрица имеет вид |
|
||||||||||||||||||||
Б |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
0 |
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
1 |
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
0 |
1 |
|
0 |
. |
|
(11.193) |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
0 |
0 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
239 |

Вероятность ошибочного приема информационного символа можно определить на основании общего выражения для ошибки приема ортогональных сигналов, полученного ранее:
|
|
|
|
|
|
|
1 |
|
|
F( x |
2Ec / N0 M 1dx , |
|
|
|
|
|
|
Pec 1 |
|
e x2 / 2 |
(11.194) |
||||||
|
|
|
|
|
|
||||||||
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
||
|
1 |
|
x |
2 |
|
|
|
|
|
|
|
|
|
где F( x ) |
|
e y |
/ 2dy – |
|
функция распределения вероятности нормаль- |
||||||||
|
|
|
|
|
|||||||||
|
|
|
|
|
|||||||||
|
|
2 |
|
|
|
|
|
|
|
|
Р |
||
|
|
|
|
|
|
|
|
|
|
|
|||
ной случайной величины с нулевым математическим ожиданием и единичной дисперсией.
С учетом вероятности ошибочного приема информационного символа,
состоящего из k log2( M ) бит (элементов), имеем вероятность ошибки при- |
|||||||||||||||||||||||||||||||||||
ема отдельного бита: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
|||||||||||||
|
|
|
|
|
k 1 |
|
|
|
|
|
k 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
|||||||
Pb |
|
2 |
|
|
|
Pc |
2 |
|
|
|
1 |
1 |
|
|
e x 2 |
/ 2 F( x |
|
|
|
M 1dx |
|||||||||||||||
|
|
|
|
|
|
|
|
2E / N |
0 |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
e |
|
|
|
2k 1 |
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
|
|
|
|||||||
|
|
|
|
|
|
|
2k 1 |
|
|
2 |
|
|
|
|
|
Г |
|
||||||||||||||||||
|
2 |
k 1 |
|
|
|
|
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
k |
1 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
x |
/ 2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
e |
|
|
F( x |
|
|
2kEb / N0 |
Б |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx , |
|
|
|
(11.195) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
2k 1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
где Eb Ec / k – энергия, приходящаясянаодин бит передаваемой информа- |
|||||||||||||||||||||||||||||||||||
ции. Данная оценка вероятности |
ошибки является слегка завышенной по- |
||||||||||||||||||||||||||||||||||
скольку при правильном кодировании значений девиации частоты информа- |
|
ционными символами |
е |
нос ь искажения сразу нескольких бит состав- |
|
ляющих символа, как правило, значительно ниже вероятности искажения |
||||
только одного бита (элемента). |
||||
|
|
|
|
т |
|
|
|
вероя |
|
|
11.7.3. Непрерывная фазовая модуляция (CPM) |
|||
|
|
|
и |
|
|
11.7.3.1.лО щее представление |
|||
|
б |
|
|
|
|
Обычный сигнал с частотной манипуляцией или модуляцией с частот- |
|||
ным |
|
(FSK) генерируется путѐм сдвига частоты несущей на величину |
||
сдвигом |
|
|
|
|
fd I , где I 1, 3, ..., ( M 1) . Этот вид модуляции сигналов был описан |
||||
Бвыше и по своей сути является методом модуляции без памяти (предыдущие со- |
||||
стояния сигнала никоим образом не влияют на его текущее состояние). Переход от одной частоты к другой может быть выполнен посредством M отдельных генераторов, настроенных на необходимые частоты, и выбора одной из M частот согласно частному значению передаваемого информационного символа на сигнальном интервале длиной c .
240
Однако такое резкое переключение с выхода одного генератора на выход другого в смежных сигнальных интервалах приводит к относительно большим долям боковых частотных составляющих вне основной полосы сигнала, и, следовательно, этот метод реализует радиосигналы с большей полосой частот, чем это необходимо для передачи сигнала. Чтобы избежать использования сигналов с большими долями боковых полос, информационный сигнал может модулировать одно несущее колебание, частота которого меняется непрерывно. Результирующий частотно-модулированный сигнал имеет в этом случае непрерывную фазу и поэтому назван частотной манипуляцией (модуляцией) с непрерывной фазой (CPFSK или CPM). Этот вид сигнала имеет память, обусловленную тем, что фазу несущей заставляют быть непрерывной и, следовательно, обеспечивают влияние предыдущих состояний сигнала на его текущее состояние.
Сигнал с непрерывной фазой может быть записан следующим образом: |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Р |
|
|
|
s( t ) A0 cos 0t ( t,a ) 0 , |
|
|
И |
(11.196) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
где |
|
|
|
|
|
|
|
|
|
У |
|
|
|
|
|
|
|
|
|
|
|
Г |
|
|
|
||
( t ,a ) 2 hk ak q( t k c ) ; |
|
|
|
|
|
|
|||||||
|
|
Б |
|
|
|
|
|||||||
|
|
k |
|
|
|
|
|
|
|
|
|||
|
t |
|
|
|
|
|
|
|
|
|
|
||
q( t ) g( )d , |
|
|
|
|
|
|
|
|
|||||
|
|
|
а |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
к |
|
|
|
|
|
|
|
где ak – текущее значение модулирующ го параметра, принимающее одно |
|||||||||||||
из M возможных значений |
1, 3, ..., ( M 1) |
в зависимости от предавае- |
|||||||||||
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
мого информационного символа; g( ) – нормированный формирующий им- |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
пульс частотной ман пуляциит, g( )d 1/ 2 |
, |
обладающий длительностью |
|||||||||||
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
g L c |
|
|
|
|
|
– |
индекс угловой модуляции |
||||||
, L – обычно натуральное число; hk |
|||||||||||||
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
(модуляция hk h |
яв яется одноиндексной – SHPM, в противном – муль- |
||||||||||||
тииндексной –лMHPM). |
|
|
|
|
|
|
|
|
|
|
|||
|
g( t ) 0 |
для t c , сигнал называют сигналом с полным откли- |
|||||||||||
|
б |
|
для t c , модулированный сигнал называют сигналом с |
||||||||||
ком. Если g( t ) 0 |
|||||||||||||
Если |
|
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
|
|
|
|
|
|
частичным (парциальным) откликом. Очевидно, что неограниченное число разновидностей сигналов непрерывной фазой можно генерировать выбором различных импульсов g( ) и изменением индекса модуляции h и размера
алфавита M .
Для текущего шага модуляции ( t ( n 1) c ,n c ) фаза сигнала с полным откликом может быть записана:
241
n 1
( t,a ) 2 hnanq( t n c ) hk ak 2 hnanq( t n c ) n . (11.197)
k
Параметр n представляет собой накопление (память) от всех информационных символов, переданных ранее до текущего шага модуляции.
11.7.3.2. Наиболее часто используемые виды формирующего импульса частотной манипуляции
Прямоугольный формирующий импульс (Rectangular REC) иногда называют LREC, где L обозначает число, соответствующее отношению
g / c длительности формирующего импульса к длительности передаваемого |
||||||||
|
|
|
|
|
|
|
|
Р |
символа. Нормированный прямоугольный формирующий импульс может |
||||||||
быть представлен следующим образом: |
|
|
|
И |
||||
|
|
|
|
|
|
|
||
|
1 |
|
|
|
|
У |
|
|
|
|
|
|
|
|
|
||
|
2 g |
, |
0 t g |
. |
Г |
|
(11.198) |
|
g( t ) |
|
|
|
|||||
|
|
|
|
|
|
|
||
|
|
для других t |
|
Б |
|
|
|
|
0, |
|
|
|
|
|
|||
В этом случае закон изменениякаф зы модулированного радиосигнала на интервале времени, соотв тствующем k-му шагу модуляции, принимает
следующий вид (здесь и далее для простоты, рассматриваем случай одно индексной модуляции):
|
|
|
о |
|
|
|
t k g |
|
|
|
|
|
g |
|
|
|
|
g |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
k 1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
и |
i тk |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
( t ,a ) 2 h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
a |
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
2 g |
|
|
t k |
|
|
|
|
|
|
|
|
|
|
||||
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
,( k 1) |
|
|
|
|||||||||||
|
л |
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
и |
|
k 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h ai |
hak |
|
|
|
|
0, g |
|
hak |
|
|
|
|
k 1 |
t 0, g |
(11.199) |
||||||||||||||
|
i |
|
|
|
|
|
|
g |
|
t |
|
|
|
|
|
|
g |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
В этом случае результирующий радиосигнал на k-м шаге модуляции |
|||||||||||||||||||||||||||||
Бпредставляется следующим выражением: |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
s( t ) A |
|
cos( t a h |
t |
|
k 1 |
). |
|
|
|
|
(11.200) |
|||||||||||||||||
|
|
|
0 |
|
|
|
|
|
0 |
|
k |
|
g |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
242
Наибольшее распространение из всех возможных вариантов реализации данной схемы модуляции получил метод минимальной манипуляции (MSK), для которого g c b , ak 1 и h 0,5 . Данный метод манипуля-
ции будет рассмотрен более подробно ниже.
Если в качестве формирующего выбран приподнятый косинусоидальный импульс (Raised Cosine RC или LRC), то его аналитическое выражение будет следующим:
1 |
|
|
|
2 t |
|
|
|
|||
|
|
|
1 |
cos |
|
|
|
, |
0 t g ; |
Р |
|
|
|
|
|||||||
g( t ) 2 |
|
|
|
|
|
|
|
|
||
g |
|
g |
|
|
(11.201) |
|||||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
И |
||
0, |
|
|
для других t . |
|
||||||
|
|
|
|
|||||||
Нормированный формирующий импульс при спектрально приподнятом косинусоидальном импульсе (Spectrally Raised Cosine SRC или LSRC) опре-
деляется следующим образом: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 t |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
2 t |
|
|
|
|
|
|
|
|
Г |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
sin |
|
|
|
|
|
cos |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
g |
|
g |
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
0 t |
|
|
; 0 1 ; |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
2 t |
|
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
g |
|
|
|
|
||||||||||||
|
g( t ) g |
|
|
|
|
|
|
|
|
|
|
|
|
4 t |
|
|
|
|
|
Б |
|
|
(11.202) |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
к |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
g |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
g |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
0, |
|
|
для других t . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
1 |
|
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Формирующий импульс при простой частотной модуляции (Tamed |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
8 |
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Frequency Modulation TFM) определяется выражением |
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
g( t ) |
|
|
g0( t c ) 2g0 |
( t ) g0( t c ) ; |
|
|
|
|
|
|
(11.203) |
|||||||||||||||||||||||||||||
|
|
л |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 t |
|
|
|
|
t |
|
|
t |
|
2 |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
t |
1 |
|
|
|
|
|
|
c |
|
|
ctg |
c |
|
|
c |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Б |
g0( t ) sin |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
(11.204) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
б |
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
24 t |
3 |
|
|
|
|
|
|
|
|
|
|
|||||||||
и |
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
Гауссовский формирующий импульс (Gaussian) обычно используется |
|||||||||||||||||||||||||||||||||||||||||
совместно с обеспечением условий |
минимальной |
|
манипуляции |
( c b , |
|||||||||||||||||||||||||||||||||||||
ak 1 и h 0,5 ), при этом схема модуляции получила наименование – гаус-
совская минимальная манипуляция (GMSK). В этом случае формирующий импульс представляется в виде
243

|
|
|
|
|
|
|
2( B )2 t2 |
|
|
|
|
B |
|
|
2 |
|
|
|
|||
g( t ) |
b |
|
|
|
|
exp |
b |
, |
0 Bb b Bb c 1. |
(11.205) |
2 |
|
ln( 2 ) |
|
ln( 2 ) |
||||||
|
|
|
|
|
|
|
||||
Данный метод модуляции будет рассмотрен более подробно несколько
ниже.
На рис. 11.28 приведены временные функции, соответствующие рассмотренным нормированным формирующим импульсам.
Соответствующие рассмотренным формирующим импульсам фазовые
|
t |
|
|
отклики |
|
|
|
|
11.7.3.3. Общие принципы демодуляции сигналов с CPMР |
|
|
|
|
Иквазиопти |
- |
мальной |
|
основывается |
на |
расчете |
значений функционала (функции) правдоподобияГУдля всех |
возмож- |
|
ных состояний полезного сигнала, вызываемых процессом модуляции. Решение о значении передаваемого информационного символа формируется на
основании сравнения рассчитанных зн чений функционала правдоподобия и |
|||||||||||||||
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
определения того состояния полезного сигн ла, которое обеспечивает его |
|||||||||||||||
максимальное значение. |
|
|
|
|
а |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
c |
|
к |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
* |
|
|
|
||||
P( X |
m ) exp |
|
|
X ( t ) S m( t ) X ( t ) S m( t ) |
dt |
|
, |
(11.206) |
|||||||
|
|
|
|||||||||||||
|
|
|
N |
|
|
|
е |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|||
m |
( t ) – m -е сост ян е п лезного сигнала, вызваное процессом модуля- |
|
где S |
||
|
|
т |
ции. |
о |
|
|
||
Особенность с гналов с CPM заключается в наличии «памяти» сигнала |
||
|
и |
|
о предыдущих передаваемых информационных символах. Данная память не |
||
позволяетбсделать однозначное сопоставление состояний полезного сигнала и конкретных передаваемых информационных символов, кроме того, для сигналов с парциальным откликом (длительность формирующего импульса
Бпревосходит длительность информационного символа) существует явление наложения модуляционных откликов от группы соседних передаваемых символов друг на друга.
244
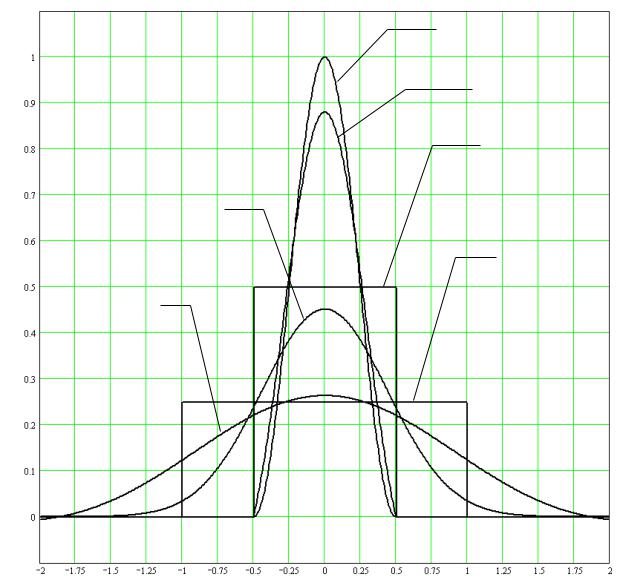
g(t)
|
|
|
|
|
|
|
|
|
|
|
1RC |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1SRC =0,5 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1REC |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Р |
|||
|
Gaussian Bb c=0,3 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
||||||
|
|
|
|
|
|
|
|
|
|
|
У |
|
2REC |
|
||||||
|
|
TFM |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
Г |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
к |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Основные |
|
|
|
|
|
|
|
|
|
|
|
t/ c |
||||
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
л |
|
нормированные формирующие импульсы |
||||||||||||||||
|
Рис. 11.28. |
|
|
|||||||||||||||||
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Рассмотрим состояния полезного сигнала подробнее. Как было показа- |
||||||||||||||||||||
но выше, с гнал с CPM в общем виде записывается выражением (11.196). |
||||||||||||||||||||
Б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рассмотримбk -й шаг модуляции, для которого запишем |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( t ,a ) 2 hiaiq( t |
i i ) |
|
|
|
|
|
|
|
(11.207) |
|||||||
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
или
245
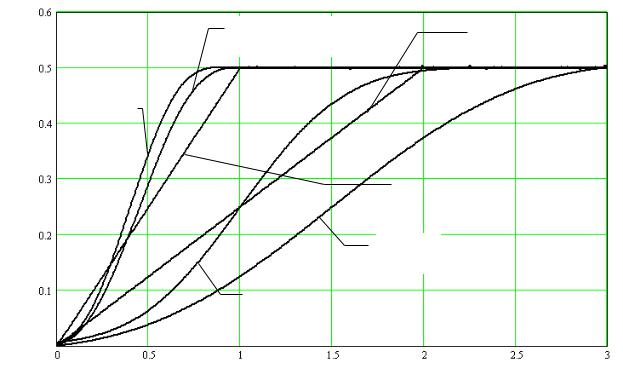
|
k L |
|
|
k |
|
( t ,a ) 2 hiaiq( t i c ) 2 |
hiaiq( t i c ) |
|
|||
|
i |
|
i k L 1 |
|
|
k L |
|
k 1 |
|
|
|
hiai |
2 |
hiaiq( t i c ) 2 hk ak q( t k c ) |
|
||
i |
i k L 1 |
|
|
||
k L ( t ,ak 1 ,...ak L 1 ) k ( t ,ak ) . |
(11.208) |
||||
|
|||||
При этом k ( t,ak ) 2 hk ak q( t k c ) представляет отклик на текущий |
|||||
|
|
|
|
|
Р |
символ модуляции (который необходимо «опознать» в процессе демодуля- |
|||||
ции); ( t ,ak 1,...ak L 1 ) 2 |
k 1 |
|
|
||
hiaiq( t i c ) |
представляет так называемую |
||||
|
|
i k L 1 |
И |
||
|
|
|
|
||
коррелированную память сигнала или неустановившиеся (незаконченные) |
||||||||||||||||||
отклики от L 1 предыдущих передаваемых |
|
|
|
У |
||||||||||||||
информационных символов; |
||||||||||||||||||
|
k L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k L hi ai представляет некоррелированную память или установивши- |
||||||||||||||||||
|
i |
|
|
|
|
|
|
|
|
Б |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
еся (законченные) отклики от всех остальных предудущих переданных сим- |
||||||||||||||||||
волов. |
|
|
|
|
|
|
|
|
|
а |
|
Г |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
q(t) |
|
|
|
|
|
|
|
к |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
1SRC |
=0,5 |
|
|
|
|
|
|
2REC |
|
|||
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
1RC |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
л |
|
|
|
|
|
|
|
|
|
1REC |
||||||
|
б |
|
|
|
|
|
|
|
|
|
|
|||||||
и |
|
|
|
|
|
|
|
|
|
|
TFM |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Б |
|
|
|
|
|
|
Gaussian Bb c=0,3 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
t/ c
Рис. 11.29. Фазовые отклики при различных видах формирующих импульсов
Таким образом, состояния полезного сигнала для подстановки в выражение для функционала правдоподобия можно определить следующим образом:
246
sm( t ) A |
cos t |
|
( t,a ) ( t,a |
|
,...a |
|
) |
k L |
(11.209) |
|||||
|
0 |
|
0 |
|
k |
k |
k 1 |
|
k L 1 |
|
|
|||
или в терминах комплексной огибающей: |
|
|
|
|
|
|
|
|
||||||
m |
( t ) A e |
j |
|
( t ,a ) ( t ,a |
,...a |
) |
k L . |
|
|
|
(11.210) |
|||
S |
|
k |
k |
k 1 |
k L 1 |
|
|
|
|
|
|
|||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
По своей сути k ( t , ak ) ( t , ak 1 ,...ak L 1 ) k L |
представляет собой |
|||||||||||||
фазовую траекторию (путь) полезного сигнала под воздействием модулирующих информационных символов. Таким образом, задача демодулятора сводится к нахождению наиболее близкой фазовой траектории полезного сигнала из всех возможных (разрешенных) к фазовой траектории наблюдаемой
Поскольку метод модуляции CPM относится к методамИдискретной модуляции, то достаточным является рассмотрение (сравнение) не непосред-
смеси сигнала и шума. |
У |
Р |
|
ственно фазовых траекторий, а их «узловых точек» (значений фазовой траек-
тории в моменты времени соответствующие моментам смены информацион- |
|||||||||
ных символов tk k c , |
k 0,1, 2,.... |
|
|
Г |
|||||
|
Как было показано выше, поиск |
|
|
функционала правдоподо- |
|||||
бия равноценен определению результирующейБфазы принимаемой смеси |
|||||||||
сигнала и |
|
|
шума в |
момент о онч ния |
информационного символа |
||||
|
|
c |
|
|
|
максимума |
|
||
|
|
|
XQ ( t )dt |
к |
|
|
|||
* |
|
0 |
|
|
|
|
|||
|
arctg |
|
|
|
, |
е |
|
|
|
|
c |
|
|
|
|||||
|
|
|
|
|
|
|
|||
|
|
|
X I ( t )dt |
|
|
|
|
||
|
|
0 |
|
|
|
|
|
|
|
где |
X I ( t ) и XQ( t ) – синфазная и квадратурная компоненты комплексной |
||||||||||||||||
огибающей входной |
т |
|
|
и поиска наиболее близкого из |
|||||||||||||
сигнала и помехи, |
|||||||||||||||||
разрешенных |
|
|
|
о |
|
|
|
|
состояний |
сигнала |
|||||||
|
|
|
фазовых |
|
|
||||||||||||
|
k |
(( k 1) |
c |
,a |
k |
) (( k 1) |
,a |
k 1 |
,...a |
k L 1 |
) |
k L и соответственно иденти- |
|||||
|
|
|
|
|
|
смеси c |
|
|
|
||||||||
фикации переданного символа ak . |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
л |
|
|
|
|
|
|
|
|
||
|
|
|
Нео ходимо отметить, что число возможных фазовых состояний сиг- |
||||||||||||||
|
|
|
|
б |
|
|
|
|
|
|
|
|
|
||||
нала в общем случае оказывается достаточно большим, например, для одно- |
|||||||||||||||||
индексной модуляции с памятью на L символов и индексом модуляции |
|||||||||||||||||
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|||
Б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
h m / p число возможных фазовых состояний равно 2 pM L 1 при нечетном
m и pM L 1 при четном m , что приводит к громоздкости и большой вычис-
лительной сложности процедуры принятия решения о передаваемом информационном символе. Без потери оптимальности громоздкость процедуры демодуляции может быть уменьшена за счет исключения так называемых «не выживших» фазовых путей в соответствии с процедурой (алгоритмом) Витерби, определенной для декодирования циклических кодов.
247
11.7.3.4.Минимальная манипуляция (MSK)
Рассмотрим сигнал с PCM для случая бинарной модуляции ( ak 1) с полным откликом (длительность формирующего импульса равна длительности информационного импульса g c b ), прямоугольной формой фор-
мирующего импульса (1REC) и индекса модуляции, равного h 0,5 . В этом случае радиосигнал на k -м шаге модуляции можно записать
|
|
|
|
|
s |
|
|
( t ) A |
cos( t a |
|
t |
|
|
|
) |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
msk |
k |
|
|
|
|
|
k 1 |
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|
|
b |
|
|
|
|
t 0, b |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
(11.211) |
|
|
|
|
|
|
A |
|
cos(( |
|
a |
|
|
|
1 |
|
)t |
|
|
) |
|
|
|
|
|
; |
|
|
Р |
|||||||||||||||
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
k |
1 |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
0 |
|
0 |
|
|
|
b |
|
|
|
|
|
|
t 0, b |
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Г |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k 1 |
|
|
|
|
|
|
|
|
|
|
У |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
k 1 |
|
h ai . |
|
|
|
|
|
|
|
|
|
(11.212) |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Сравним данный сигнал с сигналом бинарной частотной манипуляции, |
||||||||||||||||||||||||||||||||||||||||||
девиация частоты которой равна d |
|
|
|
|
. |
|
|
Б |
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
s |
( t ) A cos(( |
a |
|
|
1 |
|
|
)t ) |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
bfsk |
|
|
|
|
|
0 |
|
|
|
0 |
|
|
|
|
2 а |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(11.213) |
||
|
|
|
|
|
|
|
|
|
|
т |
|
к |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|||||||||||||||||
|
|
A |
|
cos( t )cos( |
|
|
|
1 |
t ) |
a |
sin( t ) sin( |
|
t ) . |
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
0 |
|
|
|
|
0 |
|
|
|
|
еk |
|
|
|
|
0 |
|
|
|
2 b |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
о |
|
2 |
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
На рис. 11.30 приведены временные функции данных сигналов, моду- |
||||||||||||||||||||||||||||||||||||||||||
лированных од нак в й |
нф рмационной последовательностью. |
|
|
|||||||||||||||||||||||||||||||||||||||
Как видно |
з р сунка, |
отличие двух сигналов заключается в наличии |
||||||||||||||||||||||||||||||||||||||||
|
|
л |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
скачков фазы на |
|
в |
гнале с частотной манипуляцией. |
|
|
|
||||||||||||||||||||||||||||||||||||
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Рассмотримсигнал с OQPSK, у которого в качестве квадратурных не- |
||||||||||||||||||||||||||||||||||||||||||
сущих |
сигна ов |
используются |
|
не |
|
гармонические колебания cos( 0t ) и |
||||||||||||||||||||||||||||||||||||
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin( 0t ) , а квадратурные биения вида cos( d t )cos( 0t ) и sin( d t )sin( 0t ) : |
||||||||||||||||||||||||||||||||||||||||||
Бгде I |
soqpsk ( t ) A0 I2k cos( d t )cos( 0t ) I2k 1 sin( d t )sin( 0t ) , |
(11.214) |
||||||||||||||||||||||||||||||||||||||||
1 и |
I |
2k 1 |
|
1 |
– потоки четных и нечетных элементов (по порядку |
|||||||||||||||||||||||||||||||||||||
2k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
следования) некоторого потока I , определяемого последовательностью пе- |
||||||||||||||||||||||||||||||||||||||||||
редаваемых символов ak . Элементы потоков I2k |
|
и I2k 1 |
имеют удвоенную |
|||||||||||||||||||||||||||||||||||||||
по сравнению с потоком I |
длительность и определнным образом сфазирова- |
|||||||||||||||||||||||||||||||||||||||||
ны с колебаниями cos( d t ) и sin( d t ) (рис. 11.31).
248

MSK
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Р |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
BFSK |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
t |
|
|
|
|
|
Рис. 11.30. Сравнение сигналов с MSK и BFSK |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Г |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos( d t ) |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
к |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
I2k |
т |
|
|
|
|
|
sin( d t ) |
|
|
|
|
||||||||
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
л |
|
|
|
2 b |
|
|
|
|
|
|
|
|
|
|
I2k-1 |
|
|
|
|
|
|||
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
и |
|
|
Рис. 11.31. Фазирование потоков I2k |
и I2k 1 |
|
|
||||||||||||||||||||
Б |
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Преобразуем выражение, отображающее сигнал с OQPSK, следующим |
||||||||||||||||||||||||||
образом: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s |
|
( t ) A I |
cos( t )cos( t ) |
I2k 1 |
sin( t )sin( t ) |
, |
(11.215) |
|||||||||||||||||||
|
|
|||||||||||||||||||||||||
oqpsk |
|
|
0 |
2k |
|
|
|
d |
|
|
0 |
|
|
I2k |
|
|
|
d |
0 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
soqpsk ( t ) A0I2k cos( dt )cos( 0t ) I2k 1I2k sin( dt )sin( 0t ) . |
(11.216) |
|||||||||||||||||||||||||
249

Данный сигнал представляет собой BFSK колебание, модулированное результатом перемножения I2k 1I2k и дополнительно манипулированное по
фазе на 0 или четными модулирующими символами I2k .
Записанные выражения для сигнала с OQPSK справедливы для интер-
валов времени постоянства элементов I2k и I2k 1 |
длительностью b (соот- |
||||||||||||
ветствующего временному положению элементов исходного потока I ). |
|||||||||||||
Построим временные диаграммы для данного сигнала с OQPSK |
|||||||||||||
(рис. 11.32). |
|
|
|
|
|
|
|
|
|
|
|
|
|
I(t) |
|
|
|
|
|
|
|
|
|
|
|
|
Р |
I(t)I(t- b) |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I2k-1 |
|
|
|
|
|
|
|
|
|
|
|
И |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
У |
|
|
|
|
|
|
|
|
|
|
|
Г |
|
|
||
I2k |
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
sI(t) |
|
|
|
|
|
|
к |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
sQ(t) |
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
л |
|
|
|
|
|
|
|
|
|
|
|
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
s(t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
|
|
|
|
|
|
I(t)I(t- b) |
|
|
|
|
|
|
|
|
|
|
|
|
|
t
Рис. 11.32. MSK как OQPSK
250

Как видно из рисунка, сигнал soqpsk ( t ) является сигналом с MSK, мо- |
|||||||||||||||
дулированным последовательностью, соответствующей последовательности, |
|||||||||||||||
сформированной произведением следующего вида: I( t )I( t b ) . |
|||||||||||||||
Общеизвестно, что операция вида I( t )I( t b ) соответствует процеду- |
|||||||||||||||
ре преобразования кода линии вида NRZI в код линии NRZ. Таким образом, |
|||||||||||||||
можно представить обобщенную схему формирования сигнала с MSK в виде |
|||||||||||||||
структуры, изображенной на рис. 11.33. |
|
|
|
|
|
|
|||||||||
|
|
D(t) |
Преобразователь |
|
|
OQPSK |
|
|
MSK |
||||||
|
|
|
|
NRZ NRZI |
|
|
модулятор |
|
Р |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Генератор |
cos( t/(2 b)) |
Х |
|
|
И |
|||||||
|
|
|
|
|
НЧ |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
|
|
|
|
|
|
|
|
|
|
|
/2 |
|
|
ГХ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
Генератор |
cos( 0t) |
а |
|
/2 |
|
|
||||||
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
ВЧ |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
к |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Рис. 11.33. Формирование сигнала с MSK OQPSK модулятором |
|||||||||||||||
|
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
Структурная схема |
ранскодера линейных кодов NRZ-NRZI-NRZ пока- |
||||||||||||||
зана на рис. 11.34, а |
|
|
|
к довых последовательностей – на рис. 11.35. |
|||||||||||
|
|
|
|
|
|
т |
|
|
|
|
|
|
|
||
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
||
NRZ |
|
пример |
|
NRZI |
|
|
|
|
NRZ |
||||||
|
|
л |
Х |
|
|
|
|
|
|
Х |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
b |
|
|
|
|
|
|
b |
|
|
|
|
Б |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 11.34. Транскодер линейных кодов NRZ-NRZI-NRZ |
||||||||||||||
251

NRZI(t) NRZI(t- b) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Р |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Г |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
Рис.11.35. Коды линии семейства NRZ |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
Вероятность ошибки при когерентном приеме сигналов с MSK в точ- |
||||||||||||||||
ности совпадает с вероятностью ошиб и при приеме сигналов с /2-BPSK и |
||||||||||||||||
равна |
|
|
|
|
|
|
|
|
|
а |
|
|
|
|||
|
|
|
|
|
|
|
к |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
1 |
|
|
E |
|
|
|
|
|
||
|
|
|
|
|
|
е |
b |
|
|
|
|
|
(11.217) |
|||
|
|
|
|
Pe |
2 |
erfc |
N0 |
|
. |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
|||
Поскольку с гнал с минимальной манипуляцией является сигналом |
||||||||||||||||
CPM с полным |
|
коми по сути является сигналом частотной манипуля- |
||||||||||||||
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
откл |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ции с непрерывной фазой, то возможна некогерентная его демодуляция с использованиембметодов некогерентного приема сигналов с FSK.
Би11.7.3.5. Гауссовская минимальная манипуляция (GMSK)
Гауссовская минимальная манипуляция является одним из наиболее широко используемых методов CPM модуляции. С целью большего уменьшения величины спектральных составляющих модулированного сигнала вне основной полосы частот, по сравнению с сигналом просто минимальной манипуляции, при GMSK используется гауссовский предмодуляционный фильтр (гауссовская форма нормированного формирующего импульса частотной модуляции CPM). Обычно полоса пропускания предмодуляционного фильтра выбирается из условия Bb 1/ b , что соответствует случаю CPM с
252
неполным (парциальным) откликом. На рис. 11.36 приведены основные временные диаграммы, отражающие поведение фазового набега ( t,a ) и мгно-
венной девиации частоты d ( t ) в процессе модуляции информационными символами ak при Bb 0,3 / b и индексе модуляции h 0,5 , соответствую-
щем случаю минимальной манипуляции.
Вероятность ошибки при приеме сигнала с GMSK несколько проигрывает вероятности ошибки приема сигналов с просто MSK и примерно равна
|
|
|
|
|
|
|
|
|
|
1 |
|
E |
|
|
|
||
Pb |
|
erfc |
b |
|
|
, |
(11.218) |
|
|
|
|||||||
e |
2 |
|
N0 |
|
|
|
|
|
|
|
|
|
|
|
|||
0,68 |
Bb b 0,25 |
. |
|
|
|
|
|
|
|
Р |
где |
Bb b |
|
|
|
|
|
|
|
||
1 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
И |
|||
|
|
|
|
|
|
|
|
|
||
11.7.4. Квадратурная амплитудная модуляция |
У |
|
||||||||
|
|
|
|
|
|
|
|
|
||
(Quadrature Amplitude Modulation QAM) |
Г |
|
|
|||||||
|
|
|
|
|
|
|
|
|
||
Прежде чем рассматривать квадр турную амплитудную модуляцию, |
||||||||||
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
рассмотрим некоторые особенности перед чи дискретной информации на |
||||||||||
примере сигнала с 8-PSK, |
сигнальное созвездие котрого приведено на |
|||||||||
|
|
|
е |
|
|
|
|
|
|
|
рис. 11.37. Предположим, что н пр рывно передается только один символ, |
||||||||||
например «110». |
т |
к |
|
|
|
|
|
|||
Оптимальный демодулятор «вычисляет» расстояния между всеми разрешенными состояниями полезного сигнала и откликом от входной смеси переданного сигнала и шума
|
|
|
и |
c |
|
|
c |
|
|
|
|
I |
|
|
|
|
|
|
|
|
|
|
|
|
лQ |
|
I |
( t )dt j |
|
X |
I |
( t )dt , |
(11.219) |
||
|
|
|
оX X |
|
|
|
|||||
|
б |
|
0 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
и |
X ( t ) – синфазная и квадратурная компоненты комплексной |
||||||||||
где X ( t ) |
|||||||||||
огибающей входной смеси сигнала и помехи. |
|
||||||||||
Б |
|
|
|
|
|
|
|
|
|
|
|
Решен е о передаваемом символе принимается на основании выбора ближайшего к текущему отклику от входной смеси переданного сигнала и шума разрешенного состояния сигнала. На рис. 11.37 отмечены области (сектора) принятия того или иного решения.
Необходимо отметить, что отклики от входной смеси переданного сигнала и шума концентрируются в окрестности «истинного» состояния сигнала, по крайней мере при достаточно больших отношениях сигнал/шум.
253
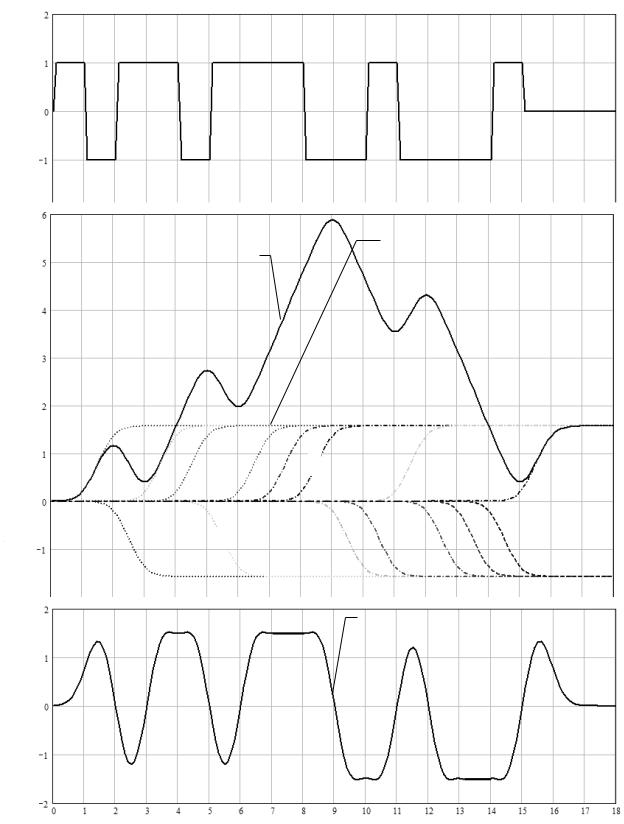
ak |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
(t,a) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Р |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Фазовые отклики отдельных |
||||||||||||
|
Совокупный |
фазовый |
|
|
|
|
|
|
|
|
|
|
|
|
информационных символов |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
набег в |
процессе |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
|
|
|
|
||||||||||||||
|
модуляции (t,a) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Г |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
к |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
4 |
|
|
6 |
|
7 |
|
8 |
|
|
|
|
|
|
|
11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
15 |
|
|
||||||
|
|
|
|
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
2 |
|
|
|
о |
5 |
|
|
|
|
|
|
|
9 |
|
|
10 |
|
|
12 |
|
13 |
|
14 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
d(t) |
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
девиация частоты d (t,a)/dt |
||||||||||||||||||
|
л |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t/ c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Рис. 11.36. Частотно-фазовые диаграммы сигнала c GMSK |
||||||||||||||||||||||||||||||||||
|
( b c 1; |
Bb b 0,3; |
h 0,5; |
ak 1; |
g |
3 b ) |
|||||||||||||||||||||||||||||
254

|
|
|
|
|
Р |
|
|
|
|
И |
|
|
|
|
У |
|
|
|
|
Г |
|
|
|
|
|
Б |
|
|
|
|
а |
|
|
|
|
к |
|
|
|
|
|
е |
|
|
|
|
|
Как видно из рис. 11.37, существует область в пределах окружности, ограничивающей энергетические (амплитудные) характеристики сигнала, в
Рис. 11.37. Диаграмма принятияр ш ний при оптимальной демодуляции сигнала с 8-PSK
приходящаяся на один символ, снизится, что позволит увеличить скорость
пределах которой возм |
д бавление дополнительных состояний сигнала |
|
|
жно |
|
(дополните ьных нформационных символов). При этом вероятность ошиб- |
||
ки, приходящаясяина один символ, практически не увеличится, а энергия, |
||
л |
|
|
б |
|
|
выс тьприпомехоустойчивость при фиксированной скорости передачи и вероятностиБош бочного приема. Однако при приеме таких сигналов наряду с точностью фазовой синхронизации опорных сигналов квадратурного преобразователя частоты существенное значение приобретает амплитудное нормирование принимаемой смеси сигнала и шума к опорным сигналам (разрешонным состояниям полезного сигнала) демодулятора.
передачи фиксированной полосе частот и вероятности ошибки, либо по-
Подобное добавление информационных символов приводит к амплитудным и фазовым изменениям радиосигнала – переносчика информации. Поскольку любое амплитудно-фазовое состояние радиосигнала может быть получено амплитудной модуляцией двух квадратурных гармонических сиг-
255

налов, подобные сигналы получили наименование сигналов с квадратурной амплитудной модуляцией (манипуляцией) или QAM, при этом, как правило, при обозначении способа модуляции указывается число возможных систояний сигнала, например 32-QAM.
В настоящее время исследовано большое количество возможных множеств сигналов QAM с целью найти структуру, которая снизит вероятность появления ошибок при данном среднем отношении сигнал/шум. На рис. 11.38 показано несколько примеров множеств символов для М = 4, 8 и 16. Обозначение (а, б, ...) соответствует сигналу, у которого а – количество сиг-
налов во внутреннем круге; б – количество сигналов на следующем круге и |
||||
|
|
|
|
Р |
т.д. В общем, правило построения «созвездия» сигнала QAM, обеспечиваю- |
||||
щего |
оптимальные |
характеристики |
(правило |
Кампопьяно– |
|
|
|
|
И |
Глейзера/Campopiano–Glazer) можно сформулировать так: из бесконечного |
||||
массива точек, плотно упакованных в регулярный массив или решетку, в качестве множества сигналов следует выбрать плотно упакованное подмножество из 2k точек. В данном случае «оптимальный» означает минимальное отношение сигнал/шум, обеспечивающее заданную вероятность ошибки. В
двухмерном пространстве сигналов оптимальная граница, окружающая мас- |
|
|
У |
сив сигнальных точек, стремится к окружности, а наиболее плотной является |
|
Г |
|
гексагональная решетка. По сравнению с квадратной кольцевая граница дает |
|
улучшение характеристик помехоустойчивости всего на 0,2 дБ. |
|
Б |
|
Кодирование состояний информ ционными символами обычно осу- |
|
ществляется в соответствии с кодом Грея (соседние состояния должны отли- |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
|
|
|
|
|||
чаться друг от друга только одним эл м нтом), что позволяет уменьшить ве- |
|||||||||||||||||||||||||
роятность ошибки, приходящ йся кна один элемент (бит) передаваемой ин- |
|||||||||||||||||||||||||
формации. Пример подобного кодирования для «квадратной» 16-QAM при- |
|||||||||||||||||||||||||
веден на рис. 11.39. |
|
е |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Вероятность |
шиб чн го приема сигналов с квадратной M-QAM (ко- |
||||||||||||||||||||||||
дирование кодом Грея) пределяется следующим образом: |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
1 |
|
|
1 |
|
|
|
3log2( M ) |
|
Eb |
|
|
||||||||
|
|
Pb |
|
|
|
erfc |
|
|
|
. |
(11.220) |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
e |
|
|
M |
|
2 |
|
|
|
|
|
|
M 1 |
|
2N |
|
|
|
|
||||
|
|
|
иlog ( M ) |
|
|
|
|
|
|
|
|
0 |
|
|
|||||||||||
|
|
л |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
В случае «неквадратной» QAM вероятность ошибки, приходящаяся на |
|||||||||||||||||||||||||
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
од н нформационный символ, удовлетворяет следующему условию: |
|
||||||||||||||||||||||||
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Pc ( M 1) |
erfc |
dmin |
|
, |
|
|
|
|
|
(11.221) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
e |
|
|
2 |
|
|
|
|
|
4N |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
где dmin2 – минимальное «расстояние» между разрешенными состояниями со-
звездия сигнала.
Прием сигналов с QAM осуществляется в соответствии с решающим правилом, описанным для случая многопозиционной фазовой манипуляции M-PSK, при этом каждое разрешенное состояние сигнала (информационный
256

символ) определяется комплексным числом, соответствующим изображаю- |
||||||||||||||||
щей точке на сигнальном созвездии. Кроме того, при формировании сигналов |
||||||||||||||||
с |
QAM |
|
возможно |
|
использование |
формирующих |
импульсов |
( |
||||||||
gF ( t ) 0 |
t 0, c ; |
c |
– длительность информационного символа) для кон- |
|||||||||||||
троля спектральных характеристик формируемого сигнала. |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Р |
|
|
|
|
4-QAM |
|
|
|
|
|
4-QAM |
|
|
И |
|
|||
|
|
|
|
|
|
|
|
|
|
8-QAM |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Г |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
к |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
е |
|
|
|
8-QAM |
|
|
|
|
|
|
16-QAM |
|
|
|
т |
16-QAM |
|
|
|
|
||||
|
|
|
|
|
|
|
|
(1,7) |
|
|
||||||
|
|
|
|
|
|
|
|
(4,12) |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
л |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
и |
|
|
|
|
|
|
32-QAM |
|
|
32-QAM |
|
||||
Б |
|
16-QAM |
|
|
|
|
|
|
|
|
||||||
|
(8,18) |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
Рис. 11.38. Примеры сигнальных созвездий |
|
|
|
||||||||
|
|
|
|
|
квадратурной амплитудной манипуляции |
|
|
|
||||||||
257

0000 |
0100 |
1100 |
1000 |
0001 |
0101 |
1101 |
1001 |
0011 |
|
0111 |
|
|
1111 |
|
1011 |
Р |
||
|
|
|
|
|
|
|
|
|
|
|
0010 |
|
0110 |
|
|
1110 |
|
1010И |
|||
|
|
|
|
|
|
|
|
У |
|
|
Рис. 11.39. Примеры кодирования кодом Грея состояний сигнала 16-QAM |
||||||||||
|
|
|
|
|
|
|
|
Г |
|
|
11.8. Спектральные характеристики излученияБ |
при дискретной |
|||||||||
полосовой модуляции |
|
|
|
а |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
11.8.1. Основные принципы определения спектральных характе- |
||||||||||
|
|
|
|
|
к |
|
|
|
||
ристик сигналов с дискр тной полосовой модуляцией |
|
|||||||||
|
|
|
|
е |
|
|
|
|
||
В большинстве сис ем цифровой радиосвязи имеющаяся в распоряже- |
||||||||||
нии полоса частот |
|
граничена. Как следствие, проектировщик системы дол- |
||||||||
жен рассмотреть, |
как граничениет |
полосы частот канала влияет на выбор |
||||||||
техники модуляц |
, |
спользуемой при передаче информации. Из этих сооб- |
||||||||
|
|
о |
|
|
|
|
|
|
|
|
ражений д я нас важно определить спектральные характеристики радиосиг- |
||||||||||
налов с цифровойимодуляцией, рассмотренных в подразд. 11.7. |
|
|||||||||
Поско ьку информационная последовательность случайная, сигнал |
||||||||||
л |
|
|
|
|
|
|
|
|
|
|
ц фровой модуляции является случайным процессом. Нас интересует спек- |
||||||||||
тральнаябплотность мощности (распределение мощности по частоте) такого |
||||||||||
Бпроцессаи. Исходя из спектральной плотности мощности, можно определить полосу частот канала, необходимую для передачи модулированного сигнала.
Определим общие подходы к нахождению спектральной плотности мощности сигналов с цифровой модуляцией.
Известно, что в соответствии с теоремой Винера–Хинчина спектральная плотность мощности стационарного случайного процесса (статистические характеристики которого не изменяются во времени) связана преобразованием Фурье с его автокорреляционной функцией.
258

|
|
S( ) K( )e j d . |
(11.222) |
|
|
Автокорреляционная функция случайного процесса x( t ) |
в свою оче- |
редь определяется следующим образом: |
|
K( ) x( t )x( t ) , |
(11.223) |
где . – обозначение операции статистического усреднения по ансамблю |
|
возможных реализаций случайного процесса. Для эргодических случайных процессов операция усреднения по ансамблю реализаций может быть заменена усреднением по времени одной теоретически бесконечно длинной реа-
лизации: |
|
|
|
|
|
|
|
|
|
|
|
|
|
Р |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
T |
|
|
|
|
|
|
И(11.224) |
|
K( ) x( t )x( t ) |
|
0 x( t )x( t )dt . |
|
|
||||||||||
T |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
У |
|
|
Определим некоторые полезные для последующего использования при |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
Г |
|
|
|
анализе спектральных характеристик сигнала соотношения. |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
Спектральная плотность мощности суммы двух случайных процессов |
||||||||||||||
|
Sx y ( ) |
|
|
|
j |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|||||||
|
Kx y ( )аe d |
|
|
|
||||||||||
|
|
|
|
|
|
|
к |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
y( t ))( x( t ) y( t )) e j |
|
|||||||
|
|
( x( t ) |
|
|||||||||||
|
|
|
|
|
|
|
е |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x( t ) y( t ) x( t )y( t ) x( t )y( t ) e j |
|
||||||||||||
|
|
|||||||||||||
|
|
|
|
т |
|
|
|
|
|
(11.225) |
||||
|
о |
|
|
|
|
|
|
|
|
|||||
Sx |
|
|
|
|
|
|
|
|
|
|
||||
( ) S y ( |
) Sxy ( ) S yx ( ). |
|
|
|
|
|||||||||
|
и |
|
|
|
|
|
|
|
|
|
|
|
||
равна сумме спектральных плотностей мощности исходных процессов плюс |
||||||
|
|
л |
|
|
Sxy ( ) и S yx ( ) . В случае если ис- |
|
их вза мные спектральные плотности |
||||||
ходные |
б |
|
процессы |
являются |
некоррелированными |
|
случайные |
||||||
( x( t )y( t ) |
0 и |
x( t )y( t ) 0 ), |
то спектральная плотность суммы |
|||
и |
|
|
|
|
|
|
(Бразности) двух случайных процессов равна сумме их спектральных плотностей.
Спектральная плотность мощности произведения двух случайных процессов
259

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Sx y ( ) |
|
K x y ( )e j d |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(11.226) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x( t )x( t )y( t )y( t ) e j . |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В случае если случайные процессы являются независимыми, можно |
||||||||||||||
сделать следующие преобразования: |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
) e j |
|
|
|
|
|
|||
Sx y ( ) x( t )x( t )y( t )y( t |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x( t )x( t ) y( t )y( t ) e j d |
|
|
)K y ( )e j d . |
|
|
|||||||||
|
|
K x ( |
|
(11.227) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Р |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Учитывая то, что преобразование Фурье от произведения двух функ- |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
|
|
ций равно свертке Фурье образов этих функций, окончательно имеем |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
|
|
|
|
|
|
|
|
|
|
|
( )S |
|
( )d . |
|
|
|
|
||
|
|
S |
x y |
|
S |
x |
y |
|
|
|
(11.228) |
|||||
|
|
|
|
|
|
|
Г |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
Необходимо заметить, |
|
|
|
|
|
|
|
|
|
|
||||
|
|
что рассм трив емые выше спектральные плот- |
||||||||||||||
ется как удвоенная спек ральная плотность в положительной области частот;
ности действительных случайных процессов являются четными функциями |
||
частоты (т.е. определены в области |
|
а |
|
положительных, так и отрицательных |
|
|
ак |
|
частот); распределение мощности р ального случайного процесса определя- |
||
е |
|
|
тной |
|
|
условие некоррелированнос и выполняется всегда, если случайные процессы не пересекаются во времени или не имеют совпадающих частотных компо-
нент (не пересекаются в част |
области). |
||||
При спектральном анализе радиосигналов с цифровой модуляцией сле- |
|||||
дует различать две |
|
о |
|
||
|
х разновидности. |
||||
К первым |
|
них относятся сигналы с так называемой линейной моду- |
|||
|
|
из |
|
||
|
л |
|
|
||
ляцией. К таким сигналам относятся все сигналы, у которых информацион- |
|||||
ная |
|
входит линейно во временную функцию сигнала, например, |
|||
s( t ) A C |
cos( t ) , где C |
1 по закону передаваемой информации. К |
|||
0бk |
0 |
|
k |
|
|
Бсигналаммодуляцияданной группы формируются с использованием рассмотренных выше схем модуляции (BPSK, /2-BPSK, QPSK, OQPSK, M-PSK, M-QAM),
к ним также могут быть отнесены сигналы FSK, M-FSK при условии прямоугольной формирующей функции частотной модуляции.
Ко вторым относятся сигналы с так называемой нелинейной модуляцией. Данные сигналы формируются схемой модуляции CPM, в которых информационный параметр нелинейно входит во временную функцию модулированного радиосигнала (в частности определяет нелинейные изменения фа-
260

зы радиосигнала во времени). Ввиду достаточной сложности рассматривать их не будем.
11.8.2. Спектральные характеристики сигналов с линейной модуляцией
Выше мы определили, что спектральная плотность мощности случайного процесса полностью определяется его автокорреляционной функцией
(11.222). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Определим |
|
автокорреляционную функцию модулированного радио- |
||||||||||||||||||||||||||
сигнала через его комплексное представление: |
|
|
|
|
|
Р(11.229) |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
* |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
K( ) |
2 |
Re s( t )s |
( t ) , |
|
|
|
И |
|||||||||
|
|
|
|
|
j 0t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
и |
|
комплексная огибающая модулированного ра- |
|||||||||||||||||||||||
где s (t) S (t)e |
|
|
|
|
|
S (t) |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
|
|
диосигнала. С учетом этого автокорреляционная функция записывается сле- |
|||||||||||||||||||||||||||||
дующим образом: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Г |
|
|
||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
||||||
|
|
|
K( ) |
Re S( t )S* ( t |
) e j 0 Re K |
|
( )e j 0 |
, |
(11.230) |
||||||||||||||||||||
|
|
|
|
S |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
где K |
S |
( ) |
|
S( t )S* ( t |
) |
– авто орр ляциионная функция комплексной |
|||||||||||||||||||||||
|
|||||||||||||||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
к |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
огибающей. |
|
|
|
|
|
|
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Осуществив преобразование Фурье от автокорреляционной функции |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
|||||
модулированного ради сигнала, получим следующее выражение для спек- |
|||||||||||||||||||||||||||||
тральной плотности: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S( ) |
|
оS ( ) ( ) ( ) d |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
S |
|
|
|
|
|
|
0 |
|
|
0 |
|
|
|
(11.231) |
||
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
1 |
S |
|
|
( ) S |
|
( ) |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
S |
S |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|||
|
|
|
л2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
где SS ( ) – спектральная плотность мощности комплексной огибающей мо- |
|||||||||||||||||||||||||||||
|
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
дул рованного сигнала. Таким образом, для определения спектральной плот- |
|||||||||||||||||||||||||||||
ностиимощности модулированного сигнала достаточно определить автокор- |
|||||||||||||||||||||||||||||
реляционную функцию |
и спектральную плотность мощности комплексной |
||||||||||||||||||||||||||||
огибающейБ . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Для сигналов с линейной модуляцией комплексная огибающая в общем |
||||||||||||||||||||||||||||
виде записывается следующим образом: |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
S( t ) |
gF ( t k c )Ik , |
|
|
|
|
|
(11.232) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|||
261

где gF ( t ) 0 t 0, c – формирующий импульс; c – длительность информационного символа (символа модуляции); k – текущий номер передаваемого информационного символа; Ik – в общем случае комплексное число,
представляющее информационный символ, принимающее конечный ряд известных значений и являющееся константой на интервале времени действия
информационного символа. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
Например, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
BPSK I |
|
A cos(C ) j sin( C ) ; |
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
k |
|
|
|
|
0 |
|
|
|
k |
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
||
|
M-PSK I A |
cos( |
k |
) j sin( |
k |
) ; |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
k |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
QPSK I |
|
|
A |
0 |
|
|
C I jCQ ; |
|
|
|
|
|
|
|
|
|
|
|
|
И |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
k |
|
|
|
|
|
|
|
|
k |
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Р |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
DBPSK, DQPSK Ik |
A0 cos( k ) j sin( k ) ; |
|
|
|||||||||||||||||||||||||||||
|
M-QAM I AI jAQ ; |
|
|
|
|
|
|
|
|
|
|
|
|
У |
|
|
|||||||||||||||||
|
|
|
|
|
|
k |
|
|
|
|
m |
m |
|
|
|
|
|
|
|
|
|
|
Г |
|
|
|
|||||||
|
|
, C I |
|
I |
|
|
Q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
где C |
k |
, C I – информационные символы { 1}; |
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
k |
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
||||
k – |
разрешенные фазовые состояния сигнала; k |
– разрешенные фазовые |
|||||||||||||||||||||||||||||||
переходы; |
Am и |
|
Am |
|
амплитуды квадратурных компонент, |
определяющие |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
|
|
|
||||
место образа сигнала в сигнальном созвездии. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
Определим автокорреляционную фун цию комплексной огибающей: |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
K ( ) |
|
S( t )S* ( t |
) |
к |
|
|
|
g ( t k |
|
)I g ( t |
m )I * |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
S |
|
|
|
|
|
|
|
|
|
т |
|
|
|
|
|
|
F |
|
|
c |
|
k F |
c |
|
||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
k m |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
gF ( t k c )gF ( t m c ) Ik Im* . |
|
|
|
(11.233) |
||||||||||||||||||||||
|
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
2 k m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
Для упрощения будем считать, что модулирующий информационный |
||||||||||||||||||||||||||||||||
поток не содерж т збыт чн сти. Это означает, что все элементы Ik равно- |
|||||||||||||||||||||||||||||||||
вероятны и не зав сят друг от друга. На основании этого предположения |
|||||||||||
б |
|
|
|
|
|
|
|
|
|
||
имеем I |
I * |
0 |
|
|
. |
Тогда выражение для автокорреляционной функции |
|||||
k |
n |
лk m |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|||
переп шется следующим образом: |
|
|
|
|
|||||||
Б |
|
|
|
|
|
|
|
|
|
|
|
и |
|
1 |
|
|
|
2 |
|
|
|||
|
|
|
|
|
|||||||
|
KS ( ) |
|
|
gF ( t k c )gF ( t k c ) |
Ik |
|
|
. |
(11.234) |
||
|
|
|
|
||||||||
|
|
|
2 k |
|
|
|
|
|
|||
Как видно из полученного выражения, автокорреляционная функция комплексной огибающей является функцией не только временного сдвига ,
но и функцией абсолютного времени t . Это вызвано тем, что случайный
процесс S( t ) является циклостационарным (или периодически стационар-
ным) |
с |
периодом |
цикла, |
равным |
τc , |
т. к. |
функция |
262

gF ( t k c )gF ( t k c ) является периодичной по переменной t с пери-
k
одом c . Для получения спектральной плотности такого процесса необходи-
мо устранить зависимость от абсолютного времени путем усреднения автокорреляционной функции по времени на ее периоде. Произведя данное усреднение, получим
|
|
|
|
|
|
1 1 |
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
KS ( ) |
|
|
|
|
gF ( t k c )gF ( t |
k c )dt |
Ik |
|
|
|
|
|
|
||||||||||||||||||
|
2 |
|
c |
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
k 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Р |
||||||||
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
1 1 |
c |
|
|
c |
|
|
|
|
|
|
2 |
|
1 |
|
|
|
|
|
|
|
2 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
gF ( t )gF ( t )dt |
Ik |
|
|
|
|
gF ( t )gF ( t )dt |
|
Ik |
|
|
. (11.235) |
||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
2 c k |
k c |
|
2 |
|
|
|
|
|
|
|
|
|
2 c |
И |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
У |
|
|
|
||||
Учитывая, что |
|
|
|
|
I |
k |
|
2 – есть дисперсия информационных компо- |
||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||
нент I |
(за исключением сигналов с M-QAM 2 A2 |
/ 2 ), запишем оконча- |
||||||||||||||||||||||||||||||
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
Б |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
||||
тельное выражение для автокорреляционной функции комплексной огибаю- |
|||||||||||||||||||||
щей: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Г |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
|
|||||
|
|
|
KS ( ) |
|
|
|
к |
|
|
|
(11.236) |
||||||||||
|
|
|
|
|
gF ( t )gF ( t |
)dt . |
|||||||||||||||
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
||||
Таким образом, спектральная плотность мощности комплексной оги- |
|||||||||||||||||||||
|
|
|
|
|
|
|
т |
|
SS ( ) |
|
|
|
|
|
|||||||
бающей модулированного сигнала |
|
|
полностью |
определяется видом |
|||||||||||||||||
формирующего импульса |
gF ( t ):е |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
о |
|
|
|
|
2 , |
|
|
|
|
|
|||||||
|
|
|
|
|
|
S |
S |
( ) |
G( ) |
|
|
|
|
(11.237) |
|||||||
|
|
л |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
где G( ) – Фурье-образ (результат прямого преобразования Фурье) функции |
|||||||||||||||||||||
gF ( t ). |
б |
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Окончательно имеем спектральную плотность мощности модулиро- |
|||||||||||||||||||||
ванного рад |
осигнала |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
и |
S( ) |
1 |
G( ) |
|
2 |
|
G( ) |
|
2 . |
(11.238) |
|||||||||||
|
|
|
|||||||||||||||||||
|
|||||||||||||||||||||
|
|
|
|
2 |
|
|
|
0 |
|
|
|
|
|
|
0 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Таким образом, выбор соответствующего вида формирующего импульса полностью определяет спектральные характеристики итогового радиосигнала.
263
11.8.3.Основные виды формирующих импульсов
В настоящее время наиболее широкое распространение получили два вида формирующих импульсов.
Первый из них – прямоугольный формирующий импульс
1, |
|
t |
|
|
c . |
|
|
|
|
||||
gF ( t ) |
|
|
|
|
(11.239) |
|
|
|
|
|
|||
0 |
|
|
|
|
|
|
Второй вид формирующих импульсов объединяет группу импульсов, получаемых путем пропускания прямоугольных импульсов через особый фильтр нижних частот, называемый фильтром Найквиста, или фильтром с
характеристикой типа приподнятого косинуса. Амплитудно-частотная харак- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Р |
|
теристика фильтра Найквиста записывается следующим образом: |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
|
|
|
|
1, |
|
|
f |
|
|
|
1 |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Г |
|
|
|
|||||
|
|
1 |
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
||||||||||||||||||||||||||
H( f ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
f |
|
|
|
|
|
|
|
|
|
|
) |
|
|
|
|
|
|
|
|
|
f |
|
|
|
|
, |
|
(11.240) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
2 |
|
1 cos |
|
|
|
|
|
|
2 c |
|
|
|
|
, |
|
|
2 c |
|
2 c |
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
0, |
|
|
f , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
2 c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
где 2 c F ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
к |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
F – полоса пропускания фильтра по уровню минус 3 дБ. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Когда 0 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
характеристика |
(АЧХ) |
фильтра |
||||||||||||||||||||||||||
|
|
ампли удно-частотная |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
станивится идеально прям угольной, при 1 |
АЧХ фильтра представляет |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
собой в чистом |
|
|
|
|
|
|
|
|
прип днятую косинусоиду |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
1 |
1 |
cos |
|
|
|
f , |
|
|
|
|
f |
|
|
1 |
, |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
||
|
|
|
|
виде |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(11.241) |
||||||||||||||
|
H( f ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
л0, |
|
f |
|
|
|
|
|
1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Импульсная характеристика (отклик на воздействие в виде дельта |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
функции) такого фильтра описывается выражением |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
Б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin |
c |
cos |
2 c |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
h( t ) |
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
(11.242) |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
t |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
c2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
264
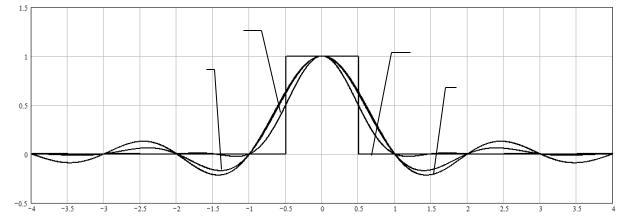
Форма формирующего импульса полностью соответствует импульсной характеристике формирующего фильтра.
На рис. 11.40 приведены временные функции основных формирующих импульсов. Как видно из рисунка, длительность формирующего импульса Найквиста значительно превосходит длительность модулирующего символа, что вызывает наложение откликов от различных модулирующих символов друг на друга.
gF(t)
Рассмотрим спектральные мехара теристики указанных выше формирующих импульсов (см. рис. 11.41). Как видно из рисунка, использование фор-
|
Найквиста = 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Прямоугольный |
|
|
||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|||
Найквиста = 0,35 |
|
|
|
|
|
И |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
Найквиста = 0, |
|||||
|
|
|
|
|
|
||||
|
|
|
|
|
|
У |
|
|
|
|
|
|
|
|
|
идеальныйРФНЧ |
|||
|
|
|
|
Б |
|
|
|
||
|
|
|
|
Г |
|
t/ c |
|||
|
|
|
а |
|
|
|
|||
|
Рис. 11.40. Различные виды формирующих импульсов |
|
|
||||||
|
|
|
к |
|
|
|
|
|
|
мирующих импульсов, отличающихся от прямоугольных, позволяет повы-
сить спектральную эфек ивнос ь |
ода модуляции (спектр модулированно- |
|||||||
|
|
|
|
го |
|
|
|
|
го радиосигнала соответс |
спек ру формирующего импульса при усло- |
|||||||
вии сдвига частотн й |
си в |
блас ь частоты f0 ) с 0,5 бит (символ)/Гц для |
||||||
|
|
|
и |
|
|
|
||
случая прямоугольн |
|
ф рмирующеговует |
импульса до практически теоретиче- |
|||||
|
|
л |
|
|
|
|
|
|
ского предела 1 б т (с мвол)/Гц для формирующего фильтра Найквиста ( |
||||||||
0 ). |
б |
|
|
|
|
|
|
|
Кроме того, использование более «сложных формирующих импульсов |
||||||||
и |
|
|
|
|
|
|
|
|
позволяет значительно (на десятки децибел) снизить излучение вне основной |
||||||||
полосы частот. |
|
|
|
|
|
|
||
Б |
|
|
|
|
|
|
|
|
Использование формирующих импульсов Найквиста требует организации значительной «памяти» о предыдущих символах модуляции в модулированном сигнале (в идеале формирующий импульс Найквиста имеет ненулевые значения на интервале времени , .
На рис. 11.42 иллюстрируется эффект от усечения длительности формирующего импульса Найквиста всего восемью интервалами c . Если вни-
мательно рассмотреть области вне основной полосы частот, то видно, что усечение длительности формирующего импульса значительно повышает внеполосное излучение. Вместе с тем даже увеличенный уровень внеполосного излучения значительно ниже аналогичных уровней, реализуемых с по-
265

мощью прямоугольных формирующих импульсов. В связи с этим современные системы цифровой радиосвязи в условиях жесткого ограничения занимаемой полосы частот, как правило, используют спектрально-эффективные многопозиционные методы модуляции с формирующими импульсами (формирующими фильтрами) Найквиста со значением параметра 0,35 , признаным стандартным.
G(f/ c),
дБ Прямоугольный
|
|
|
|
|
|
|
|
|
|
|
|
|
Р |
|
|
|
|
|
|
|
|
|
|
|
|
И |
|
|
|
|
|
|
|
|
|
|
|
У |
|
||
|
|
|
|
|
|
|
|
|
Г |
|
|
||
|
|
|
|
|
|
|
Найквиста = 0,35 |
|
|
||||
|
|
|
|
|
|
|
|
|
Б |
|
|
Найквиста = 0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
идеальный ФНЧ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
||
|
|
|
|
|
|
|
|
Н йквиста = 1 |
|
|
|
|
|
|
|
Рис. 11.41. Спекральные характеристики различных |
|||||||||||
|
|
|
|
|
т |
к |
|
|
|
|
f/ c |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
и |
формирующих импульсов |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
л |
|
|
|
|
|
|
|
|
|
|
|
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
|
|
|
|
|
|
266
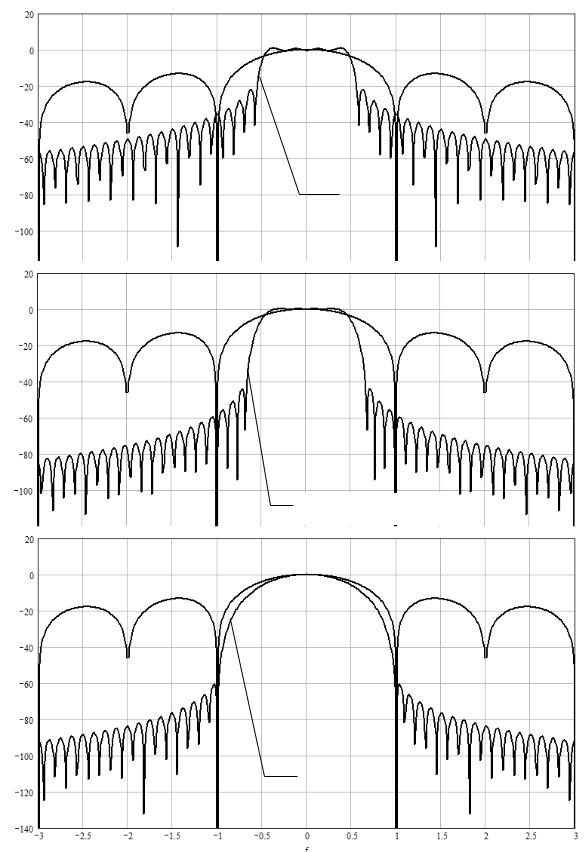
G(f/ c), дБ
|
|
|
|
|
|
|
|
|
|
Найквиста = 0, |
|
Р |
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
идеальный ФНЧ |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
|
|
|
|
|
|
|
|
|
|
|
|
|
Г |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|||
|
|
|
|
|
|
|
Найквиста |
|
|
|
|
|
|||
|
|
|
|
|
|
е |
|
|
= 0,35 |
|
|
|
|||
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
л |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Б |
|
|
|
|
|
|
|
Найквиста = 1 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||
f/ c
Рис. 11.42. Влияние усечения во временной области формирующего импульса на уровень излучения вне основной полосы частот
267
11.9.Сигнально-кодовые конструкции (Trellis Coded Modulation)
11.9.1.Место и роль сигнально-кодовых конструкций в цифровой радиосвязи
Приступая к рассмотрению основных принципов составления сигналь- но-кодовых конструкций, следует заметить, что принципиально любое наложение информации на физический носитель следует трактовать как сигналь- но-кодовую конструкцию. Таким образом, термин «сигнально-кодовая» кон-
струкция не является самостоятельным. В связи с этим необходимо уточнение, что имеется в виду, когда используется данная терминология.
информации является физический объект – он же источник информацииР. Поскольку свойства источника, в которых заложена информация, весьма разнооб-
Для этого обратимся к обобщенной структуре системы передачи инфор-
разны и, как правило, плохо пригодны для унифицированнойИпередачи, информация (физический объект-носитель), поступающая от источника, преобразует-
мации (рис. 11.43, представлена только передающая часть). Носителем любой
ся первичным преобразователем в вид, удобный для осуществленияУ унифици-
рованных процедур обработки и передачи. ПоБсутиГ, первичный преобразова-
тель преобразует один вид физического носителя (неудобный в использовании) в другой вид носителя, который удобноисточникаиспользовать в дальнейшем.
Далее преобразованный физический носитель (сигнал) поступает в кодер источника. Назначение кодера – выделения из сигнала «чистой» информации, т.е. той информациик, которую необходимо передать. Необходимость в кодере источника возникает из-за того, что сигнал обычно
содержит избыточные сведения, придающие «окраску» передаваемой ин- |
|
|
е |
формации, например при передаче голосовой команды, как правило, не ва- |
|
жен тембр и прочие с бенн с и голоса. |
|
В случае |
льз вания для передачи информации двоичных символов |
«0» и «1» кодер |
т |
ст чн ка, в идеале, должен формировать на своем выходе |
|
последовате ьность двочных символов, каждый из которых несет один бит |
|
исп информациибл(т.е. все элементы последовательности должны быть взаимоне-
зависимыми и равновероятными), кроме того, общее количество информации,исодержащееся в данной последовательности, должно точно соответствовать кол честву информации, которое необходимо передать. Это означает, Бчто скажен е любого из символов данной последовательности наносит одинаковый ущерб передаваемой информации.
Сформированная кодером сигнала последовательность отражается модулятором (в соответствии с принятой схемой модуляции) в радиосигнал – носитель информации. Таким образом, формируется сигнально-кодовая конструкция (код кодера источника-радиосигнал модулятора). Никаких особенностей формирования сигнально-кодовой конструкции не наблюдается при использовании бинарных схем модуляции. В этом случае каждому двоичному символу ставится в соответствие свой сигнал-носитель (два символа и два сигнала). При таком соответствии не нарушается правило – расстояние меж-
268
ду передаваемыми символами (расстояние по Хеммингу) должно быть согласовано с расстоянием между сигналами (расстояние Евклида). То есть меньшее растояние по Хеммингу – меньшее растояние по Евклиду и наоборот.
Источник информации
|
|
|
|
|
Первичный |
|
|
|
|
|
|
||||
|
|
|
|
|
преобразователь |
|
|
|
|
|
Р |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Кодер |
|
источника |
|
|
|
И |
||||
|
|
|
|
|
|
|
|
|
|
|
|
У |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
Кодер |
|
канала |
|
Г |
|
|
|
|||
|
|
|
|
|
|
|
Б |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Кодер |
а |
|
|
|
|
|||||
|
|
|
|
манипуляционного |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
кода |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
е |
|
|
|
|
|
|
||||
|
|
|
|
|
Модулятор |
|
|
|
|
|
|
||||
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
|
Формирователь ССК |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 11.43. Обобщенная структура передающей части канала передачи |
|||||||||||||||
|
л |
о |
информации |
|
|
|
|
|
|
||||||
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Нео ходимость выполнения данного правила можно пояснить следу- |
|||||||||||||||
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ющим о разом. Как известно из предыдущего материала, вероятность того, что вместо переданного символа при демодуляции будет принято решение о передачеБдругого символа тем меньше, чем больше расстояние по Евклиду между сигналами, представляющими данные символы. Вместе с тем величина ущерба передаваемой информации искажением одного символа другим будет тем больше, чем больше расстояние по Хеммингу между данными символами. Из этого вытекает, что большему расстоянию по Хеммингу между символами должно соответствовать большее расстояние по Евклиду между представляющими их сигналами (больший ущерб с меньшей вероятностью).
При бинарной модуляции модулятор использует поочередно по одному элементу из сформированного кодером источника потока символов. Если
269
следующие друг за другом символы одинаковы, то расстояние по Хеммингу между ними равно нулю (расстояние по Хеммингу определяется как число позиций, в которых отличаются символы одинаковой длины или разрядности, например, между шестизначными символами 010110 и 110101 растояние по Хеммингу равно трем). При этом модулятор последовательно излучает
один и тот же сигнал si ( t ) , например, при BPSK A0 cos( 0t ), растояние по
Евклиду между последовательно излученными сигналами равно нулю (растояние по Евклиду определяется как расстояние между точками, отображающими радиосигнал на комплексной плоскости). Сигнал A0 cos( 0t ) отоб-
ражается точкой A0 на действительной оси. В случае если следующие друг за другом символы различны, то расстояние по Хеммингу между ними равно
1. При этом модулятор последовательно излучает, например, |
сигнал |
|
A0 cos( 0t ) для первого символа и сигнал A0 cos( 0t ) (точка A0 |
на дей- |
|
|
Р |
|
ствительной оси) для второго символа. Расстояние по Евклиду между дан- |
||
ными сигналами равно 2A0 . Другие ситуации невозможны. И |
|
|
Повышение помехоустойчивости возможно внесением изменений в |
||
У |
|
|
схему модуляции (увеличение A0 , увеличение энергии, приходящейся на |
||
один передаваемый бит) или применением канальногоГкодера (помехоустой- |
||
чивого кодирования). Канальный кодер вносит избыточность в «чистую» |
|
информационную последовательность, позволяющуюБ |
обнаруживать и ис- |
правлять ошибки. Данная избыточность проявляется в возникновении допол-
модуляции (падает скорость п р дачи информации, вместе с информацион-
нительных элементов в модулирующей последовательности. При этом воз- |
||
|
|
а |
можны два изменения в проц |
модуляции. Первое: сохраняется скорость |
|
|
к |
|
|
ссе |
|
ными битами необходимотпередава ь еще и избыточные). Второе: сохраняется скорость передачи информации (увеличивается скорость модуляции, необходимо успевать передава ь за тоже время как информационные, так и избыточные б ты). В перв м варианте полоса частот, занимаемая радиосиг-
ние. В обоих вар антах заметна существенная эффективность использования помехоустойчивого кода.
налом, сохраняется, |
|
втором – происходит ее пропорциональное увеличе- |
|
во |
|
и |
|
|
л |
|
|
при |
|
Однозначность формирования сигнально-кодовых конструкций пропа- |
|
дает |
спользовании многопозиционных схем модуляции (M-PSK, |
Б |
|
M-QAMбпр.). Необходимость использования многопозиционных методов |
|
модуляц |
вызывается требованиями увеличения скорости передачи инфор- |
мации при фиксированной (часто очень ограниченной) полосе частот, отводимой для модулированного радиосигнала. В этом случае каждый из M возможных несущих сигналов ставится в соответствие группе из k log2( M )
символов потока, формируемого кодером источника или канальным кодером. В этом случае принципиальной становится процедура модуляционного коди-
рования (Mapping Scheme).
На рис. 11.44 приведены две схемы модуляционного кодирования сигнала с 8-PSK. Как видно из рисунка, произвольный выбор схемы модуляци-
270
онного кодирования не обеспечивает выполнения условия согласований рас- |
||||||||||||||||
стояний по Хеммингу для информационных символов и по Евклиду для |
||||||||||||||||
представляющих их сигналов. |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
jy |
|
|
|
|
|
|
|
jy |
|
|
|
|
|
|
2 |
2 |
010 |
|
|
|
|
|
011 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
011 |
|
|
|
|
|
001 |
010 |
|
|
|
001 |
||||
|
100 |
|
|
|
|
|
2 |
2 |
|
000 |
|
110 |
|
|
|
000 |
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
x |
|
|
|
101 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
111 |
|
111 |
|
|
|
100 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Р |
|
|
|
|
|
|
110 |
|
|
|
|
|
101 |
И |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
Г |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
Рис. 11.44. Примеры схем модуляционного кодированияБ |
сигнала с 8-PSK |
|||||||||||||||
|
Далее рассмотрим случай |
|
|
|
информации по каналу связи с |
|||||||||||
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
||
ограниченной (фиксированной) полосой частот с использованием многопо- |
||||||||||||||||
|
|
|
|
|
|
|
|
|
к |
|
|
|
|
|
||
зиционных сигналов. Пусть реализована схема модуляции, обеспечивающая |
||||||||||||||||
заданную скорость передачи информации при фиксированной полосе частот |
||||||||||||||||
канала и заданной вероя |
|
|
передачи |
|
|
|
|
|
|
|||||||
|
|
и ошибки. Требуется повысить помехоустойчи- |
||||||||||||||
вость при сохранении пр чих параме ров качества. Одним из путей решения |
||||||||||||||||
данной задачи является применениет |
методов помехоустойчивого кодирова- |
|||||||||||||||
ния. Данные методы |
|
|
|
избыточность в передаваемый информационный |
||||||||||||
|
|
|
|
|
вносят |
|
|
|
|
|
|
|
|
|
||
сигнал, позво яющую корректировать возникающие ошибки. Ширина поло- |
||||||||||||||||
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
||
сы частот, занимаемая модулированным сигналом, определяется длительно- |
||||||||||||||||
стью |
|
|
модуляции. |
Поэтому для сохранения используемой ширины |
||||||||||||
|
|
л |
|
|
|
|
|
|
|
|
|
|
|
|
||
полосы частот для передачи избыточной информации, заложенной помехо- |
||||||||||||||||
устойч вымбкодом, необходимо использовать схемы модуляции с увеличен- |
||||||||||||||||
ным ч слом |
|
нформауционных символов. Например, если в исходном вари- |
||||||||||||||
|
символа |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
анте использовался метод модуляции 4-PSK, то при использовании кода со |
||||||||||||||||
скоростью кодирования, равной 2/3 (два информационных бита преобразу- |
||||||||||||||||
Б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ются в три бита помехоустойчивого кода), для сохранения занимаемой поло- |
||||||||||||||||
сы частот необходимо использовать уже 8-PSK схему модуляции. Из преды- |
||||||||||||||||
дущего материала известно, что при увеличении размерности используемой |
||||||||||||||||
схемы модуляции происходит снижение помехоустойчивости процесса де- |
||||||||||||||||
модуляции. В связи с этим возникает дилемма: компенсации потерь в поме- |
||||||||||||||||
хоустойчивости при увеличении размерности схемы модуляции выигрышем |
||||||||||||||||
271
от помехоустойчивого кодирования. Другими словами, приведет ли применение помехоустойчивого кодирования к выигрышу в помехоустойчивости или окажется наоборот вредным.
Если модуляция трактуется как отдельная операция, независимая от кодирования, то требуется использование очень мощных кодов (большие кодовые ограничения свѐрточных кодов или большая длина блокового кода) для возмещения потерь и обеспечение некоторого достаточного выигрыша от кодирования. С другой стороны, если модуляция является частью единого процесса кодирования и она рассчитывается совместно с кодом, для увеличения минимального расстояния (евклидового расстояния) между парами кодированных сигналов потери от расширения ансамбля сигналов легко преодолеть и достигается достаточный выигрыш кодирования при относительно простых кодах. Ключ для подхода к этой совместной модуляции и кодирова-
нию заключается в изобретении эффективного метода, отображения кодовых |
|
|
Р |
бит (символов) в сигнальные точки так, чтобы максимизировать минималь- |
|
ное евклидово расстояние между парами символов. |
И |
|
|
Таким образом становится понятной необходимость синтеза специаль- |
|
ных сигнально-кодовых конструкций, обеспечивающих оптимизацию проце- |
||
|
|
У |
дуры передачи информации. |
Г |
|
|
||
|
Б |
|
Создание методов передачи информации, в которых достигаются близ- |
||
кие к предельным показатели эффективности, требует согласования всех частей тракта передачи с учетом статистических свойств непрерывного канала.
Это означает, что кодирование и модуляцию необходимо рассматривать как |
|
е |
|
единый процесс формирования сигналаа, демодуляцию и декодирование – |
|
как процесс оптимального при ма сигнальнок |
-кодового блока в целом. Согла- |
т |
|
сование модуляции и кодирования сводится к поиску такого заполнения сиг- |
|
нального пространства, при ко ором обеспечивается высокая удельная скорость (сигналы расп л жены дос аточно плотно) и одновременно высокая помехоустойчивость (сигналы достаточно далеко друг от друга).
обработки сигнально-кодовойлконструкции. При этом декодер канала работает в метри-
Декодирован е м дуляционного кода можно рассматривать как по- |
|
следний этап |
о |
сигнально-кодового блока оптимальным декодером |
|
ке Евклидабс сигна ами, а не с их двоичными представлениями по правилу манипуляционного кода.
Бпроцессуиобъединения сигналов и кодов в единую эффективную конструкцию.
Так м о разом понятие «сигнально-кодовая конструкция» является не самостоятельным, а лишь отражает подход к модуляции и кодированию как
11.9.2.Согласование канала кодом Грея
Рассмотрим сигнально-кодовые конструкции, представляющие собой результат согласования известных двоичных помехоустойчивых кодов с многопозиционным ансамблем сигналов путем использования в качестве манипуляционного кода Грея.
272

Комбинации кода Грея получаются по следующему правилу. Кодовая комбинация исходного кода складывается по модулю 2 с такой же комбинацией, сдвинутой на один разряд вправо, при этом младший разряд сдвинутой комбинации отбрасывается (табл. 11.3).
Таблица 11.3 Пример формирования манипуляционного кода Грея
Номер |
|
Исходный |
|
|
|
Кодовая комбинация, кодирующая |
|||||
состояния |
|
|
|
|
|||||||
двоичный код |
|
|
|
состояние сигнала по правилу Грея |
|||||||
сигнала |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
||
0 |
|
|
0000 |
|
|
0000 |
– исходная комбинация |
|
|
||
|
|
|
|
|
|
|
00000 – сдвинутая комбинация |
|
|
||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
0000 |
– полученная кодовая комбинация |
|||
|
|
|
|
|
|
|
|
Р |
|||
1 |
|
|
0001 |
|
|
0001 |
– исходная комбинация |
|
|||
|
|
|
|
|
|
|
00001 – сдвинутая комбинация |
|
|
||
|
|
|
|
|
|
|
|
И |
|
||
|
|
|
|
|
|
|
0001 |
– полученная кодовая комбинация |
|||
2 |
|
|
0010 |
|
|
0010 |
– исходная комбинация |
|
|
||
|
|
|
|
|
|
|
|
|
У |
|
|
|
|
|
|
|
|
|
00010 – сдвинутая комбинация |
|
|
||
|
|
|
|
|
|
|
|
Г |
|
||
|
|
|
|
|
|
|
0011 |
– полученная кодовая комбинация |
|||
3 |
|
|
0011 |
|
|
0011 |
– исходная комбинация |
|
|
||
|
|
|
|
|
|
|
00011 – сдвинутБя комбинация |
|
|
||
|
|
|
|
|
|
|
0010 |
– полученн я кодовая комбинация |
|||
|
|
|
|
|
|
|
исходная |
|
|
||
4 |
|
|
0100 |
|
|
0100 |
– комбинация |
|
|
||
|
|
|
|
|
|
|
00100 – сдвинутая комбинация |
|
|
||
|
|
|
|
|
|
|
|
к |
|
|
|
|
|
|
|
|
|
|
0110 |
– полученная кодовая комбинация |
|||
|
|
|
|
|
|
|
е |
|
|
||
5 |
|
|
0101 |
|
|
0101 |
– исходная комбинация |
|
|
||
|
|
|
|
|
|
|
00101 – сдвинутая комбинация |
|
|
||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
0111 |
– полученная кодовая комбинация |
|||
|
|
|
|
|
т |
|
|
|
|
||
6 |
|
|
0110 |
|
|
0110 |
– исходная комбинация |
|
|
||
|
|
|
|
о |
00110 – сдвинутая комбинация |
|
|
||||
|
|
|
и |
|
|
|
|
||||
|
|
|
|
|
|
|
|||||
|
|
|
|
|
0101 – полученная кодовая комбинация |
||||||
7 |
|
|
0111 |
|
|
0111 |
– исходная комбинация |
|
|
||
|
|
л |
|
|
|
00111 – сдвинутая комбинация |
|
|
|||
|
б |
|
|
|
|
|
|
||||
|
|
|
|
|
0100 |
– полученная кодовая комбинация |
|||||
8 |
|
|
1000 |
|
|
1000 |
– исходная комбинация |
|
|
||
и |
|
|
|
|
|
01000 – сдвинутая комбинация |
|
|
|||
Б |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
1100 |
– полученная кодовая комбинация |
||||
9 |
|
|
1001 |
|
|
1001 |
– исходная комбинация |
|
|
||
|
|
|
|
|
|
|
01001 – сдвинутая комбинация |
|
|
||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
1101 |
– полученная кодовая комбинация |
|||
10 |
|
|
1010 |
|
|
1010 |
– исходная комбинация |
|
|
||
|
|
|
|
|
|
|
01010 – сдвинутая комбинация |
|
|
||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
1111 |
– полученная кодовая комбинация |
|||
273
|
|
|
|
|
|
|
|
|
|
|
Окончание табл. 11.3 |
||
1 |
|
2 |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
1011 |
– исходная комбинация |
|
|||||
11 |
|
1011 |
|
|
|
01011 – сдвинутая комбинация |
|
||||||
|
|
|
|
|
|
0110 |
– полученная кодовая комбинация |
||||||
|
|
|
|
|
|
1100 |
– исходная комбинация |
|
|||||
12 |
|
1100 |
|
|
|
01100 – сдвинутая комбинация |
|
||||||
|
|
|
|
|
|
1010 |
– полученная кодовая комбинация |
||||||
|
|
|
|
|
|
1101 |
– исходная комбинация |
|
|||||
13 |
|
1101 |
|
|
|
01101 – сдвинутая комбинация |
Р |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1011 |
– полученная кодовая комбинация |
||||||
|
|
|
|
|
|
1110 |
– исходная комбинация |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
И |
|
14 |
|
1110 |
|
|
|
01110 – сдвинутая комбинация |
|
||||||
|
|
|
|
|
|
1001 |
– полученная кодовая комбинация |
||||||
|
|
|
|
|
|
|
|
|
|
|
У |
|
|
|
|
|
|
|
|
1111 |
– исходная комбинация |
|
|||||
|
|
|
|
|
|
|
|
|
|
Г |
|
|
|
15 |
|
1111 |
|
|
|
01110 – сдвинутая комбинация |
|
||||||
|
|
|
|
|
|
1000 |
– полученная кодовая комбинация |
||||||
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
Поскольку ошибки чаще происходят за счет переходов в области со- |
|||||||||||||
седних сигналов, |
то кодовые блоки, соответствующие соседним сигналам, |
||||||||||||
|
|
|
|
|
|
|
|
а |
|
|
|
||
должны различаться наименьшим числом двоичных символов. |
|
||||||||||||
|
|
|
|
|
|
|
к |
|
|
|
|
||
На рис. 11.45 приведен пример |
одиров ния состояний сигнала (моду- |
||||||||||||
ляционного кода) для 16-QAM, в с об х у з н номер разрешѐнного состо- |
|||||||||||||
яния сигнала. |
|
|
|
высокие |
|
|
|
|
|
||||
|
|
|
т |
|
|
|
|
|
|
|
|||
Несмотря на достаточно |
|
|
|
показатели энергетической эффек- |
|||||||||
тивности, согласование кодом Гр я не является оптимальным. |
|
||||||||||||
Двоичные коды, |
|
имальные по критерию максимума хэммингова |
|||||||||||
|
|
оп |
|
|
|
|
|
|
|
|
|
||
расстояния, будут |
птимальны и по критерию максимума свободного евкли- |
||||||||||||
|
если |
|
|
|
|
|
|
|
|
|
|
|
|
дова расстояния, |
при |
|
тображении двоичных подблоков в сигнальные |
||||||||||
точки ансамбля вып лняется принцип: большему расстоянию Хэмминга соответствует большее расстояние по Евклиду.
Избрис. 11.45 видно, что наибольшее евклидово расстояние имеется,
например между 0-й и 12-й точками (сигналами), в то время как расстояние по Хеммингу между определяемыми ими кодовыми комбинациями равно 2 при макс мальном расстоянии для данного кода, равняющемся четырем, что Бговор т о неоптимальности данного варианта модуляционного кода. В связи с этим существует возможность определения более эффективных сигнальнокодовых конструкций.
274

(0) |
(7) |
(8) |
(15) |
|
|
|
0000 |
0100 |
|
1000 |
|
|
|
|
1100 |
|
|
|||
(1) |
(6) |
|
(9) |
(14) |
|
|
0001 |
0101 |
|
1101 |
1001 |
|
Р |
(2) |
(5) |
|
(10) |
(13) |
|
|
|
И |
|||||
0011 |
0111 |
|
1111 |
1011 |
||
|
|
|
||||
(3) |
(4) |
|
(11) |
У |
|
|
|
(12) |
|
|
|||
0010 |
0110 |
1110 |
Г |
|
|
|
Б |
|
|
||||
|
|
|
|
1010 |
|
|
Рис. 11.45. Примеры кодирования кодом Грея состояний сигнала 16-QAM |
||||||
|
|
к |
|
|
|
|
Согласование канала кодом Грея предст вляет собой процедуру моду-
ляционного кодирования и является дост точно оптимальным, в случае если |
|
е |
|
исходный цифровой поток не сод ржит избыточностиа |
, т.е. отсутствует кодер |
канала и кодер источника выполня т свое назначение (оставляет «чистую» |
|||||
|
|
|
|
|
т |
информацию). В противном случае сх ма манипуляционного кода Грея мо- |
|||||
жет не обеспечивать |
|
имальный разнос, обеспечивающий минимальный |
|||
|
|
|
|
оп |
|
урон в случае возникн вения шибок. |
|||||
|
|
|
и |
|
|
11.9.3. |
л |
|
|
||
|
Решетчатое кодирование (Trellis Coded Modulation) |
||||
|
б |
|
|
|
|
11.9.3.1. Общие понятия о решетчато-кодовой модуляции |
|||||
и |
|
|
|
|
|
Од н |
з возможных эффективных методов отображения кодовых бит |
||||
Б |
|
|
|
|
|
(символов) в сигнальные точки, так чтобы максимизировать минимальное евклидово расстояние (между парами символов), был разработан в 1982 г. Унгербоеком (Ungerboeck G.). На основании анализа сигнально-кодовых на базе ансамбля 8-PSK и сверточного кода со скоростью R k /( k 1) Унгер-
боек сформулировал ряд правил построения сигнально-кодовых конструкций. Сигнально-кодовые конструкции, построенные по этим правилам (Trellis-Coded Modulation – ТСМ), часто называют СКК Унгербоека.
По способу согласования модуляции и кодирования сигнально-кодовые конструкции Унгербоека относятся к конструкциям, полученным на основе разбиения ансамбля сигналов на вложенные подансамбли. Разбиение осу-
275
ществляется таким образом, что подансамбли содержат равное количество сигналов, расстояния между соседними сигналами подансамблей одинаковы, минимальные расстояния между сигналами подансамблей увеличиваются с каждым шагом разбиения.
Схемы ТСМ используют избыточную небинарную модуляцию плюс конечный автомат (кодер). Конечный автомат (или автомат с конечным числом состояний) – это общее название устройств, обладающих памятью о предыдущих сигналах, при этом существует ограниченное число однознач-
ных состояний, которые может принимать автомат. |
|
|
|
В стандартных системах, включающих модуляцию и кодирование, |
|||
|
|
|
Р |
обычно принято отдельно описывать и реализовать детектор и декодер. Од- |
|||
нако в системах ТСМ эти функции должны рассматриваться совместно. |
|||
|
|
И |
|
Можно добиться эффективного кодирования, не жертвуя скоростью передачи |
|||
данных или не увеличивая ни ширину полосы частот, ни мощность. |
|||
|
У |
|
|
При решетчатом кодировании набор сигналов многоуровневой/фазовой |
|||
модуляции комбинируется со схемой решетчатого кодирования. Термин |
|||
Г |
|
|
|
«схема решетчатого кодирования» применим к любой кодовой системе, ко- |
|||
Б |
|
|
|
торая обладает памятью (конечный автомат), например сверточный код. |
|||
Набор сигналов ТСМ наилучшим образом представляется любым |
|||
набором сигналов (более чем двоичным), векторное представление которого может быть отображено на комплексной плоскости. Унгербоек (Ungerboeck) показал, что при наличии шума схема ТСМ довольно просто может дать
суммарную эффективность кодирования, близкую к 3 дБ, по сравнению с |
||||||||||
|
|
|
|
|
|
|
|
|
|
а |
некодированной системой, а при ув личении сложности можно достичь эф- |
||||||||||
фективности порядка 6 дБ. |
|
|
к |
|||||||
Сверточное кодирование ув личивает размер множества сигнала с 2k |
||||||||||
до 2k p . Унгербоек |
|
|
|
е |
|
|||||
|
|
|
|
повышение пропускной способности, дости- |
||||||
|
|
|
|
|
|
сть |
|
|
||
|
|
|
|
|
исследовал |
|
|
|
||
гаемое благодаря увеличению набора сигналов, и пришел к заключению, что |
||||||||||
|
|
|
и |
|
|
|
|
|
||
максимальную эффект вн |
|
можно реализовать, удваивая передаваемый |
||||||||
|
|
сигналов |
|
|
|
|
|
|
||
некодированный набор (р = 1). Этого можно достичь путем кодирования со |
||||||||||
степенью |
k /(k 1) |
|
с последующим отображением групп из k 1 бит в |
|||||||
|
б |
|
|
|
|
|
|
|
|
|
набор из 2k 1 |
|
|
ов. Так, при реализации TCM со степенью кодирования |
|||||||
и |
|
|
|
|
|
|
|
|
||
2/3 на ор |
|
|
модуляции 4-PSK заменяется набором сигналов модуля- |
|||||||
ц 8-PSK, аналогично 16-QAM замещается на 32-QAM при степени коди- |
||||||||||
Б |
|
|
|
|
|
|
|
|
|
|
рован я 4/5 т.д. |
|
|
|
|
|
|
|
|||
В каждом из случаев TCM система синтеза сигнально-кодовых конструкций сконфигурирована таким образом, чтобы до и после кодирования средняя мощность сигнала была одинаковой. Кроме того, для обеспечения необходимой избыточности при кодировании размер набора сигналов увели-
чивается в два раза с M 2k до M 2k 1 . Расширенный набор сигналов при фиксированной средней мощности приводит к уменьшению расстояния между соседними точками символов, как видно из рис. 11.46. В некодированной системе такое уменьшение расстояния снижает достоверность пере-
276
дачи. Однако вследствие избыточности, вносимой кодом, это уменьшение расстояния уже не сильно влияет на вероятность ошибки. Напротив, достоверность определяет просвет – минимальное расстояние между членами набора разрешенных кодовых последовательностей. Другими словами, когда два сигнала находятся в непосредственной близости друг от друга в сигнальном пространстве кодовой системы, их близость может и не иметь существенного значения (с точки зрения вероятности ошибки), поскольку правила кода могут не допускать перехода между двумя такими, якобы уязвимыми точками сигналов. Задача TCM заключается в присвоении сигнальных точек
переходам в кодовой решетке таким образом, чтобы увеличить просвет между теми переходами (символами), которые вероятнее всего могут быть перепутаны.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Р |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
Г |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
||
|
|
|
|
|
|
A |
|
|
|
|
|
а |
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
к |
|
|
|
|
2B =A |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
16-Q AM |
|
|
е |
32-Q AM |
|
|
|
|
|
||||||||||
Рис. 11.46. Изменение рас |
|
яния между сигнальными точками при удвоении |
||||||||||||||||||
размерности схемы м дуляции и сохранении средней мощности сигнала |
||||||||||||||||||||
|
|
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
|||
11.9.3.2. |
|
Разбиение исходного ансамбля сигналов |
|
|
|
|||||||||||||||
|
л |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Поскольку сигнально-кодовые конструкции Унгербоека относятся к |
||||||||||||||||||||
конструкц ям, |
полученным на основе разбиения ансамбля сигналов на вло- |
|||||||||||||||||||
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
женные подансамбли, рассмотрим данную процедуру. Разбиение осуществ- |
||||||||||||||||||||
ляетсятаким образом, что подансамбли, содержащие равное количество сиг- |
||||||||||||||||||||
наловБ, при разбиении стремятся сохранять регулярную структуру множеств и подмножеств сигналов, при последовательном разбиении минимальные расстояния между сигналами подансамблей увеличиваются с каждым шагом разбиения, формально левая ветвь разбиения кодируется символом «0», а правая «1» для получения обозначения получаемого подмножества. На рис. 11.47 приведен пример последовательного разбиения созвездия сигнала 16-QAM на подансамбли. Из рисунка видно, что при разбиении минимальное
277

расстояние между сигналами подансамблей изменяется в следующем поряд-
ке: уровень А – A0 ; уровень B – 
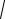 2A0 ; уровень C – 2A0 и уровень D – 2
2A0 ; уровень C – 2A0 и уровень D – 2
 2A0 , т. е. каждый уровень разбиения увеличивает расстояние между точками,
2A0 , т. е. каждый уровень разбиения увеличивает расстояние между точками,
изображающими сигнал в  2 раз.
2 раз.
Степень, до которой происходит разбиение сигнала, зависит от характеристик сигнально-кодовой конструкции кода. В общем, процесс сигнальнокодового отображения выполняется так, как показано на рис. 11.47.
Блок из k информационных символов делится на две группы длиной n и m , m символов кодируются в m p символов, в то время как n символов
остаются не кодированными. После этого m p |
Р |
символов кодера использу- |
ются для выбора одного из 2m p возможных подансамблей (используются только подансамбли одного уровня) в разделенном ансамбле сигналов, в то
время как n символов используются для выбора одной из 2n сигнальных точек в каждом подансамбле. Если n 0 , все информационные символы коди-
руются. |
|
И |
|
|
|
11.9.3.3. Конструирование сигнально-кодовойУконструкции |
||
|
Г |
|
Конструирование сигнально-кодовой конструкции расмотрим на базе |
||
примера, популярного в литературе по основ м цифровой радиосвязи. |
||
|
Б |
|
|
а |
|
Постановка задачи: необходимо повысить помехоустойчивость перда- |
||
чи двоичных сигналов в радиоканале с фи сированной полосой частот (изна- |
||
|
е |
|
чально используемая схема модуляции 4-PSK). |
||
Из предыдущего |
материала |
извкстно, что максимальная эффективность |
|
||
от использования Trellis-Coded Modulation при сохранении занимаемой поло-
|
|
го |
||
сы частот достигается при повышении размерности схемы модуляции в два |
||||
раза. На основании эт |
выберем для составления сигнально-кодовой кон- |
|||
струкции метод |
модуляции |
8-PSK (можно 8-QAM). |
||
|
|
|
||
Произведем разб ение ансамбля сигналов 8-PSK на подмножества в |
||||
л |
|
|
|
|
соответствии со схемой, приведенной на рис. 11.49. |
||||
без |
|
|
|
|
Для кодирования сигнально-кодовой конструкции примем следующую |
||||
схему. Исходными данными для кодирования являются пары символов, кодировавш е исходный сигнал 4-PSK. Один из данных символов будем ис-
Бнечныйиавтомат (кодер) со скоростью преобразования 1/2. Возможный вариант кодера приведен на рис. 11.50.
пользовать преобразований (кодирования), а второй пропустим через ко-
278
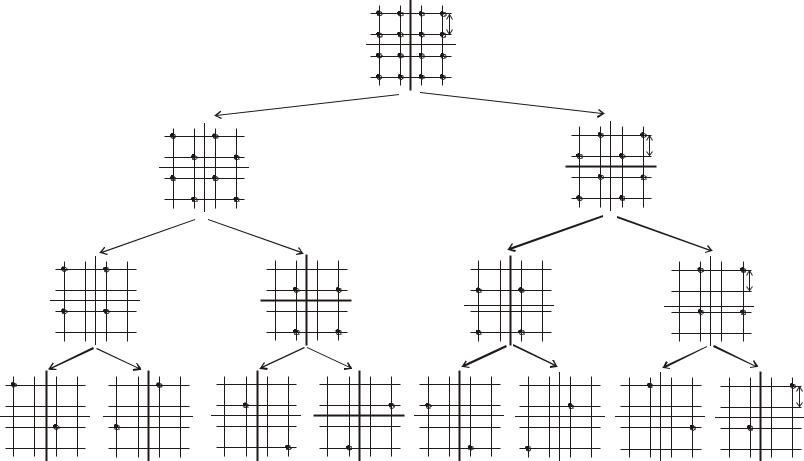
280
A
B
C
“0”
D
|
|
|
|
|
|
|
|
|
|
A0 |
|
|
|
Р |
|
|
|
|
|
“0” |
|
|
|
|
|
|
“1” |
И |
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
|
|
|
|
|
|
|
|
|
|
|
|
|
Г |
|
A0 |
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
“0” |
|
|
|
“1” |
|
|
|
а |
|
“0” |
|
“1” |
||
|
|
|
|
|
|
|
к |
|
|
|
|
|
|
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
|
“1” |
|
“0” |
|
т |
|
|
“0” |
|
|
|
“1” |
“0” |
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
л |
|
|
|
|
|
|
|
|
|
|
|
|
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 11.47. Пример разбиения множества сигнала 16-QAM на подмножества |
||||||||||||||
Б |
|
|
|
|
|
|
|
|
|
|
279 |
|
|
|
A0
“1”
A0
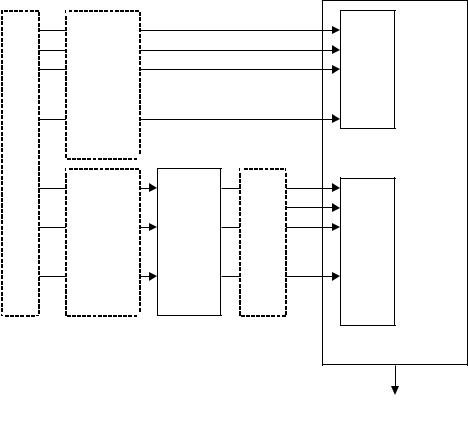
|
|
|
|
|
|
|
|
|
|
в |
сигналов подмножестве |
|
|
|
|
|
|
подвергающихся |
|
|
|
|
|
Выборподмножества Выбор сигнала |
|
|
|
|
Блок из k бит, подлежащихпередаче |
|
nбитне, |
битm для кодирования кодированию |
… … |
Кодер канала конечный( автомат) |
|
m+pкодированных бит |
|
|
Р |
||
|
|
|
… |
И |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
У |
|
|
|
|
|
|
|
|
|
|
|
|
|
Модулятор |
|
|
|
|
|
|
|
|
|
|
|
|
Г |
|
|
|
|
|
|
|
|
|
|
|
|
|
Сигнально-кодовая |
|
||
|
|
|
|
|
|
|
|
|
Б |
конструкция |
|
||
|
|
|
|
|
|
|
|
а |
|
|
|||
Рис. 11.48. Общая структура |
|
|
|
|
|
||||||||
омбинированного кодера/модулятора |
|||||||||||||
|
|
|
|
|
|
|
к |
|
|
|
|
|
|
Состояния конечного ав ома а принято обозначать двоичными симво- |
|||||||||||||
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
лами, хранящимися в элемен ах задержки, за исключением крайнего левого |
|||||||||||||
(входного). Приведенный на рисунке автомат может находиться в одном из |
|||||||||||||
четырех состояний: а = 00, b = 10, c = 01 и d = 11. |
|
|
|
|
|||||||||
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
Решетчатая д аграмма |
переходов данного автомата приведена на |
||||||||||||
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
рис. 11.51 (состав ена на основании данных табл. 11.4). |
|
|
|||||||||||
Произведя добавление некодированного бита (введение параллельных |
|||||||||||||
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
ветвей), |
по учаем полную решетчатую диаграму схема помехоустойчивого |
||||||||||||
|
|
л |
|
|
|
|
|
|
|
|
|
|
|
код рован я, приведенную на рис. 11.52. |
|
|
|
|
|
||||||||
Выполнив наложение решетчатой диаграммы на разбитое созвездие |
|||||||||||||
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
сигнала 8-PSK, получим решетчатую диаграмму сигнально-кодовой кон- |
|||||||||||||
струкциии, изображенную на рис. 11.54. |
|
|
|
|
|
|
|||||||
Б |
|
|
|
|
|
|
|
|
|
|
|
|
|
280 |
|
|
|
|
|
|
|
|
|
|
|
|
|
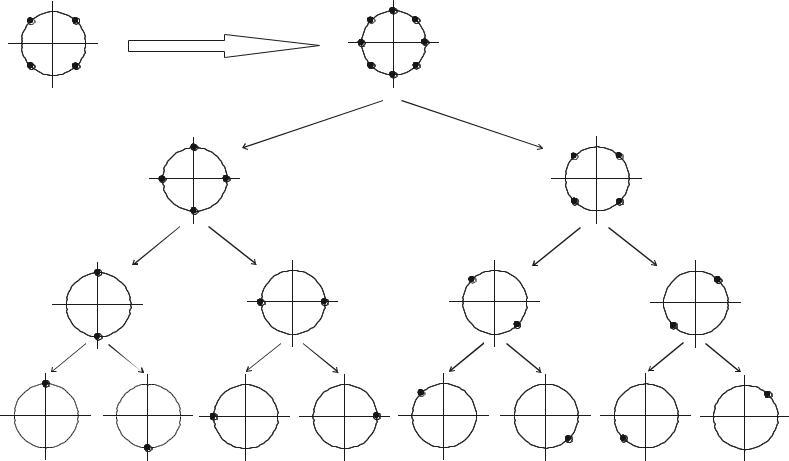
282
|
4-PSK |
|
|
|
|
8-PSK |
|
|
|
|
Р |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
И |
|
|
|
|
|
|
|
|
|
|
|
|
У |
|
|
|
|
B0 |
|
|
|
|
|
|
|
Г |
|
B1 |
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
C0 |
|
|
|
C1 |
|
к |
|
|
|
|
C3 |
|
|
|
|
|
е |
C2 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
D0 |
D1 |
D2 |
|
о |
D3 |
D4 |
|
|
D5 |
D6 |
|
D7 |
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
л |
|
|
|
|
|
|
|
|
|
|
|
|
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
и |
Рис. 11.49. Разбиение ансамбля сигналов 8-PSK |
|
|
|||||||||
|
Б |
|
|
|
|
|
|
|
281 |
|
|
|
|
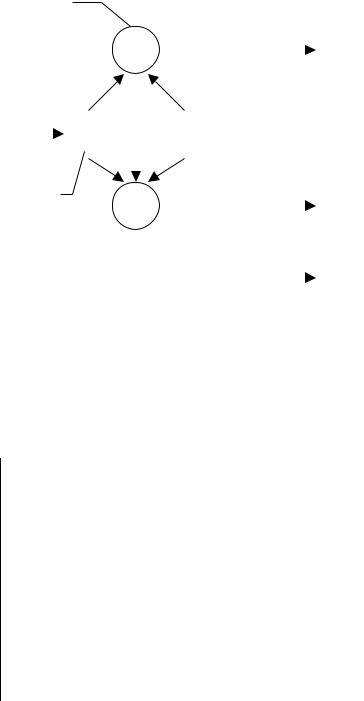
Сумматор по |2|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
c1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D |
|
D |
|
D |
|
|
|
|
|
Р |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
Элемент |
|
|
|
|
|
|
|
c2 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
задержки |
|
|
|
|
|
|
|
|
|
И |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
на такт |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c3 |
|
|
|
|
|
|
d2 |
|
|
|
|
|
|
|
|
|
Г |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
одера |
|
|
|
|
|
||
|
|
|
|
|
Рис. 11.50. Кодирующий автомат |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
к |
|
|
|
|
|
Таблица 11.4 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
Переходы |
|
|
c1c2 |
|
|
|
|
|
|||
Входной символ |
Состояние авто- |
|
Выходные сим- |
|
Следующее со- |
||||||||||||||
|
d1 |
|
|
|
|
мата |
|
|
|
|
волы |
|
|
|
|
стояние |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
0 |
|
|
|
|
00 (a) |
|
|
|
|
00 |
|
|
|
|
00 (a) |
|||
|
1 |
|
|
|
|
00 (a) |
|
|
|
|
11 |
|
|
|
|
10 (b) |
|||
|
0 |
|
|
и |
10 (b) |
|
|
|
|
01 |
|
|
|
|
01 (c) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
1 |
л |
|
10 (b) |
|
|
|
|
10 |
|
|
|
|
11 (d) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
0 |
|
|
|
|
01 (c) |
|
|
|
|
11 |
|
|
|
|
00 (a) |
|||
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
1 |
|
|
|
|
01 (c) |
|
|
|
|
00 |
|
|
|
|
10 (b) |
|||
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
11 (d) |
|
|
|
|
10 |
|
|
|
|
01 (c) |
|||
|
1 |
|
|
|
|
11 (d) |
|
|
|
|
01 |
|
|
|
|
11 (d) |
|||
Б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
282
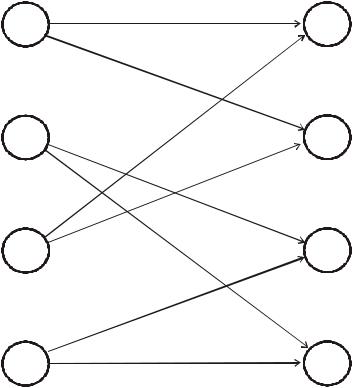
|
|
d 1 |
c1 c 2 |
|
|
|
|
|
||
00(a) |
|
0 |
00 |
|
|
|
00(a) |
|
||
|
|
|
|
|
|
|
|
|||
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
10(b) |
|
|
0 |
|
|
|
0 |
10(b) |
Р |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
1 |
0 |
|
|
|
|
|
|
|
|
|
|
|
И |
|||
|
|
|
|
|
|
0 |
0 |
|
||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
У |
|
||
|
|
|
|
|
|
|
||||
01(c) |
|
|
|
|
1 |
|
|
01(c) |
|
|
|
|
|
|
|
0 |
|
Г |
|
|
|
|
|
|
0 |
|
|
Б |
|
|
|
|
|
|
0 |
1 |
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|||
11(d) |
|
|
1 |
|
01 |
|
|
11(d) |
|
|
|
|
к |
|
|
|
|||||
|
|
|
|
|
|
|
|
|||
Рис. 11.51. Решетчатая диаграмма переходов кодирующего автомата |
||||||||||
|
|
дующие |
|
|
|
|
|
|
|
|
При наложении решетчатой диаграммы кодера на созвездие использу- |
||||||||||
|
т |
|
|
|
|
|
|
|
|
|
емого сигнала выполняются сл |
|
|
правила: |
|
|
|
||||
1. Параллельные переходы (когда они возникают) назначаются сиг-
нальным точкам, разделенным максимальным расстоянием Евклида (в нашем |
||||
примере точкам, принадлежащим одному из подмножеств С0,…,С3). |
||||
|
|
|
и |
|
2. |
Переходы, нач нающиеся (заканчивающиеся) в некотором состо- |
|||
|
л |
|
||
янии, назначаются подмножествамо |
более высокого уровня из одной ветви |
|||
разделения (в рассматр ваемом примере либо B0 (C0C1), либо B1 (C2C3)), |
||||
|
б |
|
|
|
имеющим с едующее за максимальным растояния Евклида между сигналь- |
||||
точками |
|
|
|
|
ными |
|
. |
|
|
3. |
С гнальные точки должны по возможности возникать с одинако- |
|||
Б |
|
|
|
|
вой частотой. |
|
|
|
|
На рисунке обозначения D0, …,D7 соответствуют сигналам нижнего уровня разбиения созвездия 8-PSK и показывают, какой именно сигнал излучается при переходе сигнально-кодовой конструкции из одного состояния в другое. Состояния сигнально-кодовой конструкции обозначаются CICJ в соответствии с используемыми в данном состоянии подансамблями сигналов (подансамблями выходных ветвей) CI и CJ. Кодировка сигналов D0, …,D7 определяет модуляционный код и связывает конкретные сигналы с кодом, формируемым автоматом помехоустойчивого кодирования.
283

000
00(a) |
001 |
00(a) |
|
|
10(b)
110
1 |
|
1 |
|
|
1 |
0 |
|
1 |
|
1 |
|
|
1 |
1 |
|
1 |
|
|
0 |
0 |
|
0 |
|
10(b)
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
Р |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
0 |
|
|
И |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
0 |
|
|
|
|
0 |
1 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
01(c) |
|
|
|
|
|
|
0 |
|
|
|
|
|
01(c) |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
У |
|
||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
Г |
|
|
|||||
|
|
|
|
|
0 |
|
|
|
|
|
|
|||||||
|
|
|
|
1 |
|
|
|
|
Б |
|
|
|
|
|
||||
|
|
|
|
|
|
1 |
|
|
010 |
|
|
|
|
|
||||
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11(d) |
|
|
|
|
|
011 |
|
|
|
|
|
|
11(d) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
к |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
C1 |
C2C 3 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 11.52. Р ш тчатая диаграмма переходов |
|
|||||||||||||||
|
|
|
|
помехоустойчивого кодера |
|
|
|
|||||||||||
|
|
|
го |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для рассматриваем |
|
|
примера модуляционный код определяется сле- |
|||||||||||||||
|
|
и |
т |
|
|
|
|
|
|
|
|
|
|
|
|
|||
дующим образом. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
л |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
000 D0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
001 D1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
010 D4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
011 D5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
100 D6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
101 D7
110 D2
111 D3
Два кодированных символа используются для выбора одного из четырех подобразов сигнального созвездия C0…C3, в то время как оставшийся информационный символ используется для выбора одной из двух точек внутри каждого подобраза.
284
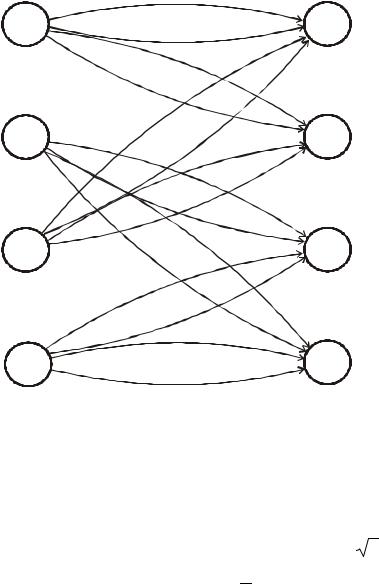
Показанная на рис. 11.53 решетка является в основе своей решѐткой для свѐрточного кода со скоростью 1/2 с добавлением параллельных путей, размещающих некодированные символы d2. Таким образом, кодированные
символы c1c2 используются для выбора одного из четырех подобразов, каж-
дый из которых содержит две сигнальные точки, а некодированные символы используются для выбора одной из двух сигнальных точек внутри каждого подобраза. Заметим, что сигнальные точки внутри подобраза удалены на расстояние 2. Таким образом, расстояние Евклида между параллельными путями равно 2.
|
|
|
|
D0 |
|
|
|
|
|
|
|
|
Р |
|
|
C0C1 |
|
|
D1 |
|
|
|
|
|
C0C1 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
D2 |
|
|
|
|
|
|
|
||
|
|
|
|
|
D3 |
|
|
|
|
|
|
|
И |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
C2C3 |
|
|
|
|
|
0 |
|
C2C3 |
|
|
|||
|
|
|
|
|
|
|
|
|
У |
|
||||
|
|
|
|
|
3 |
|
D |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
Г |
|
|
||
|
|
|
|
D |
|
|
1 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
D |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
||
|
|
|
|
|
|
D |
|
|
D5 |
|
|
|
|
|
|
C1C0 |
|
|
|
|
6 |
|
|
|
|
C1C0 |
|
|
|
|
|
|
|
D |
а |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
7 |
|
|
|
|
|
||||
|
|
|
|
|
к |
|
|
|
|
|
|
|
|
|
|
|
6 |
е |
|
|
|
|
|
|
|
|
|
||
|
D |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
7 |
|
|
|
|
|
|
|
|
|
||
|
|
D |
|
D4 |
|
|
|
|
|
|
|
|
||
|
|
|
т |
D5 |
|
|
|
|
C3C2 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
о |
|
|
|
|
|
|
|
|
|
|
|
||
Рис. 11.53. Решетчатая диаграмма сигнально-кодовой конструкции |
||||||||||||||
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
Анализ решетчатой диаграммы показывает, что некодированные сим- |
||||||||||||||
волы d2 всегдалпередаются сигналами, максимально отстоящими друг от дру- |
||||||||||||||
га (для случая 8-PSK это нормированное расстояние равно 2). Следует отме- |
||||||||||||||
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
тить, что в сходной схеме модуляции 4-PSK минимальное нормированное |
||||||||||||||
расстояниеимежду некодированными символами равнялось 2 . Таким обра- |
||||||||||||||
зомБ, помехоустойчивость передачи некодированных символов (каждого второго из передаваемых) повысилась на 20lg( 
 2 ) 3 дБ. При передаче второ-
2 ) 3 дБ. При передаче второ-
го (кодированного) символа следует также ожидать повышения помехоустойчивости, поскольку он подвергнут помехоустойчивому кодированию со скоростью 1/2 (каждый информационный символ передается двумя символами модуляции).
285
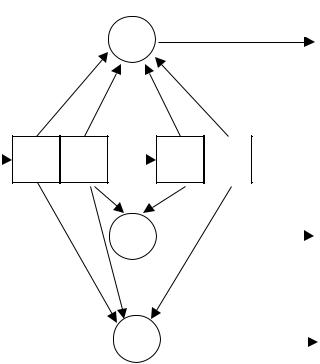
В качестве альтернативной схемы кодирования мы можем использовать кодер со скоростью 2/3 и кодировать оба информационных символа так, как, например, показано на рис. 11.54. Это кодирование ведет к решѐтке с восемью состояниями и обеспечивает лучшее качество, но требует более сложную реализацию декодера.
c1
+
Демодуляция сигналов TCM осуществляется в соответствии с прави-
|
d1d2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Р |
|
|
D |
D |
|
D D |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c2 |
И |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
Г |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
c3 |
|
||||
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
|
||
Рис. 11.54. Пример альт рнативного кодирующего автомата |
||||||||||||||||||
|
|
|
|
|
|
к |
|
|
|
|
|
|
|
|
||||
|
|
|
|
е |
|
|
|
|
|
|
|
|
|
|
||||
лами и алгоритмами, применимыми для декодирования соответствующих
помехоустойчивых к д |
, с ой лишь разницей, что в процессе декодирова- |
|
ния (демодуляц ) |
|
расчета расстояний между кодовыми конструкци- |
ями в метрике Хемм нга используется расстояние между сигнальными точ- |
||
|
вместо |
|
ками в метрике Евк да. В связи с этим процесс демодуляции – декодирова- |
||
ния для сигна овис TCM является неразрывным и единым. Кроме того, если |
||
позволяет вычислите ьная мощность демодулятора, при демодуляции сигналов с TCM широко используются так называемые мягкие методы декодиро-
ван ия, основанныеб на отслеживании большего числа возможных траекторий СКК, в той ли иной степени близких к наблюдаемой траектории входной смеси сигнала и помехи. Мягкие методы декодирования (демодуляции) ис-
Бпользуют многопороговые схемы принятия решения, позволяющие определять «степень» достоверности того или иного решения, а не только самое достоверное.
286
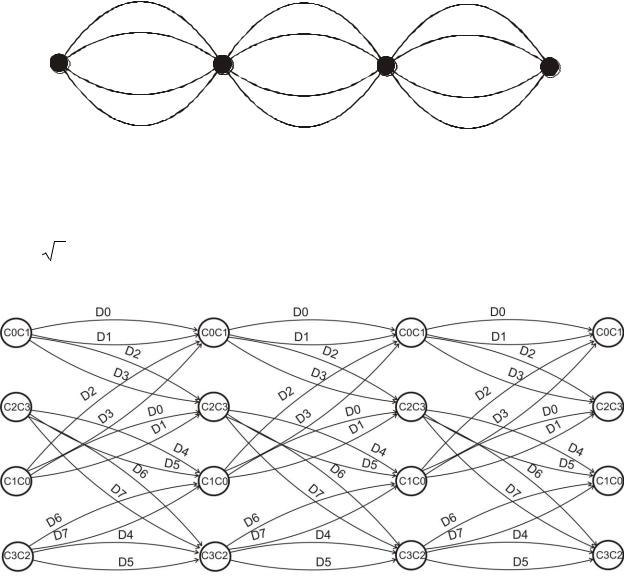
11.9.3.4. Сравнение помехоустойчивости кодированной и некодированной схем
Основные принципы сравнения помехоустойчивости кодированной (TCM) и некодированной схем модуляции проведем на основе рассмотренного ранее примера построения сигнально-кодовой конструкции.
Итак, исходная схема модуляции 4-PSK. Пусть используется набор сигналов для представления модулирующих символов, соответствующий подмножеству сигналов B1 (см. рис. 11.49). Решетчатая диаграмма данной
сигнальной конструкции приведена на рис. 11.55. |
|
|
Р |
|||||||||
|
|
D6 |
|
|
|
D6 |
|
|
D6 |
|
||
|
|
|
|
|
|
|
|
|
||||
|
|
D4 |
|
|
|
D4 |
|
|
D4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
|
|
|
|
D5 |
|
|
|
D5 |
|
Г |
И |
|||
|
|
D7 |
|
|
|
D7 |
|
Б |
D7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Рис. 11.55. Сигнально-кодовая конструкция некодированной 4-PSK |
||||||||||||
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
|
|
|
|
|
к |
|
|
|
|
|
Некодированный сигнал 4-PSK имеет одно состояние и четыре ветви, |
||||||||||||
минимальное нормированное |
растояние |
по Евклиду между которыми состав- |
||||||||||
ляет 2 . |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
т |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||
Решетчатая диаграмма рассматрива мого сигнала с TCM приведена на |
||||||||||||
рис. 11.56. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
л |
|
|
|
|
|
|
|
|
|
|
|
б |
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 11.56. Решетчатая диаграмма кодированого сигнала
Демодуляция некодированной конструкции осуществляется на одном переходе, следовательно, ее помехоустойчивость определяется квадратом расстояния по Евклиду между ветвями (сигналами), соединяющими одина-
287

ковые состояния. В расматриваемом случае это (  2 )2 2 (нормированное к
2 )2 2 (нормированное к
энергии сигнала, приходящейся на символ модуляции).
Демодуляция кодированного сигнала осуществляется путем отслеживания траектории на протяжении нескольких переходов (определяется ограничением кода). Если определить минимальное растояние между любыми двумя путями, соединяющими одинаковые состояния, на участке с более чем одним переходом, то квадрат минимального растояния между данными траекториями будет равен 4 (квадрат расстояния между кратчайшими траекториями, например, параллельными цепочками D0-D1). Поскольку помехоустойчивость определяется квадратом минимального растояния, то налицо выигрыш рассматриваемой кодированной схемы в 3 дБ по сравнению с некодированной. Больший выигрыш может быть получен использованием кодов с
большим числом состояний (позволяют исключить параллельные ветви в |
|
решетчатой диаграмме сигнально-кодовой конструкции). |
Р |
У |
|
Примечание. Квадрат расстояния между двумя траекториями опреде- |
|
Г |
|
ляется как сумма квадратов расстояний между ветвями принадлежащимиИ |
|
данным траекториям на каждом переходе. Например (см. рис. 11.56), для |
|||||
|
|
|
|
Б |
|
двух траекторий D0-D1-D0 и D3-D5-D2 квадрат расстояния равен (D0- |
|||||
D3)2+(D1-D5)2+(D0-D2)2 (обозначение DI-DJ соответствует расстоянию меж- |
|||||
|
|
|
сигнала |
|
|
ду изображающими точками в созвездии |
|
). |
|||
|
|
к |
|
|
|
11.10. Заключение |
е |
|
|
|
|
|
т |
|
|
|
|
Существует большое разнообразие возможных вариантов осуществления информационной модуляции радиосигналов. Вне зависимости от вы-
бранного способа модуляции существуют общие закономерности, присущие
всем модуляционным схемам. К аким закономерностям можно отнести сле-
дующие: и 1. Полоса зан маемых радиосигналом частот прямо пропорциональна
символьной лскорости модуляции, символ/с.
2. бВид спектра ьной плотности мощности модулированного сигнала в
значительной мере определяется видом формирующего импульса и не зависит и(для случая линейной модуляции) от конкретного вида модуляции. Б3. Спектральная эффективность радиосигнала (бит/Гц)/с, может быть повышена спользованием многопозиционных методов модуляции и соответствующим выбором вида и параметров формирующего импульса.
4. Помехоустойчивость демодуляции радиосигналов вне зависимости от вида модуляции отпределяется отношением энергии, приходящейся на один бит передаваемой информации, к спектральной плотности мощности шума наблюдения (вероятность ошибочного приема падает с ростом данного отношения).
5. Наилучшими характеристиками помехоустойчивости (при равных энергетических соотношениях) обладают модуляционные схемы, при кото-
288
рых наибольшее расстояние по Хеммингу между передаваемыми символами соответствует наибольшему расстоянию по Евклиду между сигналами, отображающими данные символы.
6.Большей эффективностью в каналах с ограниченной полосой пропускания обладают методы повышения помехоустойчивости, в которых помехоустойчивое кодирование согласовано с модуляционной схемой (сиг- нально-кодовые конструкции).
7.Оптимальный прием большинства радиосигналов с дискретной модуляцией требует точного знания фазы несущего колебания и, соответству-
ющих схем (процедур) восстановления данной информации из принимаемого сигнала при отсутствии данной информации. Р
8.Поскольку решение о значении передаваемых информационных символов принимается в дискретные моменты времени, необходимымИ условием успешной демодуляции является наличие тактовой синхронизации демодулятора с передаваемым потоком данных. УГ
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
|
|
к |
|
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
л |
|
|
|
|
|
|
|
|
б |
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
|
|
289
12.СИНХРОНИЗАЦИЯ
12.1. Общая задача синхронизации при приеме сигналов с дискретной модуляцией
Из предыдущих разделов известно, что наибольшая энергетическая и спектральная эффективность передачи дискретной информации достигается при использовании методов фазовой манипуляции, таких как BPSK, QPSK, M-PSK и М-QAM. Прием сигналов, модулированных в соответствии с данными методами, осуществляется по так называемой когерентной схеме. Данная схема предполагает точное знание частоты и фазы несущего колебания. В реальных условиях частота и фаза несущего колебания не известна. Это обусловлено особенностями распространения радиоволн, нестабильностью
частоты опорных генераторов, изменяющимся местоположением передаю- |
|
щего и приемного устройств, эффектом Доплера и пр. |
Р |
|
|
В связи с тем что параметры несущего колебания заранее определены |
|
|
И |
быть не могут, при осуществлении когерентной демодуляции сигналов необ- |
|
ходимо осуществлять оценку частоты и фазы несущего колебания. Результа- |
||
|
|
У |
|
Г |
|
Б |
|
|
ты данной оценки затем используются для компенсации возможных ошибок |
||
установки опорного колебания в демодуляторе. |
|
|
(принимаемых символов). Данная синхронизация нужна, во-первых, для правильной временной привязки проц сса генерации опорных несущих сигна-
Наряду с оценкой параметров несущего колебания процесс демодуля-
ции требует тактовой синхронизации демодулятора и потока передаваемых
лов, используемых для формирования (вычисления) значений соответствую- |
|
|
к |
щих функционалов правдоподобия; во-вторых, процедура непосредственно |
|
|
е |
принятия решения о том или ином значении принимаемого символа дискрет- |
|
на во времени (сначала пр |
энергетическое накопление результатов |
сравнения опорных к пий несущих сигналов с принятой смесью сигнала и |
|||
|
|
|
исходит |
шума, а затем, в м мент максимального накопления, обычно в конце переда- |
|||
ваемого символа, просходит принятие решения) и, в-третьих, после приня- |
|||
тия того и и иного решения необходим сброс накопительных элементов. |
|||
|
|
и |
|
Таким о разом, обобщенная структура когерентного (квазикогерентно- |
|||
го, посколькулпараметры несущего сигнала не могут быть определены с иде- |
|||
альной точностью) демодулятора приведена на рис. 12.1. |
|||
|
б |
|
|
и |
|
|
|
Б |
|
|
|
290

x(t) |
|
|
|
|
XI(t) |
|
|
|
|
Принятые |
|
|||
Квадратурный |
|
|
|
|
|
|
символы |
|
||||||
|
преобразователь |
|
XQ(t) |
|
|
Демодулятор |
|
|
|
|
|
|||
|
частоты |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Оценка |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
частоты и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
фазы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Схема оценки |
|
|
|
|
|
|
|
Синхр. |
||
|
|
|
|
частоты и фазы |
|
|
Схема |
|
|
Римпульсы |
||||
|
|
|
(ошибки установки |
|
восстановления |
|
||||||||
|
|
|
|
|
тактовой |
|
|
|||||||
|
|
|
частоты и фазы) |
|
|
|
|
|||||||
|
|
|
|
|
|
|
И |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
несущего |
|
|
синхронизации |
|
|||||
|
|
|
|
|
|
|
|
У |
|
|||||
|
|
|
|
|
колебания |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
Г |
|
|
|
|
|
|
Рис. 12.1. Обобщенная структура квазикогерентного демодулятора |
|||||||||||||
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
Квадратурный преобразователь ч |
|
осуществляет перенос приня- |
|||||||||||
того радиоколебания в область |
|
|
частоты, при этом на его выходах |
|||||||||||
формируются сигналы, |
представляющие действительную и мнимую части |
|||||||||||||
комплексной огибающей приня |
|
к |
|
|
Демодулятор по |
|||||||||
|
см си сигнала и шума. |
|||||||||||||
результатам обработки комплексной огибающей входной смеси сигнала и |
||||||||||||||
шума формирует на |
|
|
|
нулевой |
|
|
|
|
|
|
||||
|
|
выходе оценки принятых информационных сим- |
||||||||||||
волов. Работа демодуля |
|
ра синхронизирована с потоком принимаемых ин- |
||||||||||||
формационных с мв л в сигналами тактовой синхронизации, |
сформирован- |
|||||||||||||
|
|
|
|
|
той |
|
|
|
|
|
|
|
|
|
ными схемой восстановления тактовой синхронизации. Схема восстановле- |
||||||||||||||
|
|
|
своем |
|
|
|
|
|
|
|
|
|
||
ния тактовой синхрон зац и в качестве входного сигнала использует проме- |
||||||||||||||
|
|
и |
|
|
|
|
|
|
|
|
|
|
||
жуточные резу ьтаты обработки комплексной огибающей в демодуляторе |
||||||||||||||
(может непосредственно |
использовать комплексную огибающую). Схема |
|||||||||||||
|
|
л |
|
|
|
|
|
|
|
|
|
|
|
|
оценки частоты и фазы (ошибки установки частоты и фазы) несущего коле- |
||||||||||||||
бан я на босновании обработки комплексной огибающей входной смеси сиг- |
||||||||||||||
нала |
шума формирует оценку данных параметров, |
которая используется |
||||||||||||
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
для формирования опорного колебания квадратурного преобразователя ча- |
||||||||||||||
стоты либо для коррекции сигналов комплексной огибающей в демодуляторе |
||||||||||||||
Б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(показано пунктирной линией). Процесс оценки частоты и фазы может со- |
||||||||||||||
провождаться снятием информационной модуляции (так называемая обрат- |
||||||||||||||
ная связь по решению показана пунктирной линией). |
|
|
|
|
|
|||||||||
|
Следует отметить, что точность оценки частоты и фазы (синхрониза- |
|||||||||||||
ции по несущему сигналу) оказывает сильное влияние на реализуемые веро- |
||||||||||||||
ятности ошибочного приема сигналов с дискретной модуляцией. |
|
|||||||||||||
291
12.2. Методы восстановления несущего колебания при полосовой демодуляции
Известны два базовых подхода для обеспечения синхронизации по несущей в приѐмнике. Один сводится к замешиванию на передаче специального сигнала, называемого пилот-сигналом, который можно извлечь из принимаемого сигнала и по его частоте и фазе синхронизировать местный опорный генератор. Когда по каналу передана одновременно немодулированная несущая (пилот-сигнал) и информационный сигнал, приѐмник использует замкнутую петлю фазовой автоподстройки (ФАП, PLL), чтобы захватить и отслеживать несущую. ФАП рассчитывается так, чтобы реализовать узкую полосу пропускания и тем самым обеспечить слабое воздействие частотных
компонент информационного сигнала на ее работу. |
|
|
Р |
||
|
|
|
|
|
|
Второй подход сводится к непосредственной оценке фазы несущей по |
|||||
|
|
|
|
И |
|
|
|
|
У |
|
|
модулированному сигналу. Этот подход имеет отчѐтливое преимущество, |
|||||
|
|
Г |
|
|
|
поскольку вся мощность передатчика направлена на передачу информацион- |
|||||
ного сигнала. |
Б |
|
|
|
|
|
|
|
|
|
|
Поскольку реализация первого подхода более или менее прозрачна, |
|||||
ограничим наше внимание вторым подходом. |
|
|
|
|
|
|
а |
|
|
|
|
Сложность оценки фазы несущего сигн ла непосредственно по моду-
несущее колебание в чистом виде. кИ поэтому для осуществления синхрони-
лированному сигналу заключается в том, что, как правило, спектр сигнала с
цифровой модуляцией (особенно при использов нии схем требующих только когерентного детектирования) несод ржит составляющих, представляющих
зации по несущему колебаниют, в п рвую очередь, необходимо получить дан-
ные составляющие свободные от информационной модуляции. В настоящее время известны два осп с ба получения компонент, несущих информацию о фазе несущей и свиб дных информационной модуляции. К первому отно-
сятся так называемые мет ды с обратной связью по решению. В данной группе методов результаты демодуляции информационных символов по-
вторно модублируют принятый сигнал для снятия с него информационной составляющей. Второй способ заключается в использовании особенностей сигнальногоисозвездия используемого метода модуляции, благодаря которым путем определенного нелинейного преобразования принятого сигнала можно Босуществ ть «съем» информационной модуляции (методы не управляемые решением).
Рассмотрим эти методы получения информации о фазе несущего сигнала более подробно.
12.2.1.Максимально правдоподобная оценка фазы
Из предыдущего материала известно, что максимально правдоподобная оценка неизвестного параметра сигнала (в нашем случае мгновенной началь-
292
ной фазы ( t ) ( t ) 0 ), где ( t ) – неизвестная ошибка установки частоты; 0 – неизвестная начальная фаза) определяется исходя из условия
|
|
|
|
||
|
ln P( X |
( t )) |
0 , |
(12.1) |
|
( t ) |
|||||
|
|
( t ) # ( t ) |
|
||
|
|
|
|
||
где # ( t ) – оптимальная в соответствии с методом максимального правдо-
подобия оценка неизвестной фазы сигнала. Здесь необходимо подчеркнутьР , что значение оценки фазы сигнала производится в каждый момент времени, т.е. оценка является текущей (решается задача непрерывной фильтрации неизвестного параметра сигнала). Опустив громоздкие выкладки, запишем обобщенное правило формирование текущей оценки параметра сигнала для
случая его наблюдения на фоне белого гауссовского шума в установившемся |
||||||||||||||||
режиме. |
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
||
|
|
|
|
|
1 |
|
|
|
|
|
|
У |
* |
|
||
L # ( t ) K |
|
|
|
X ( t ) S( t, # ( t )) X ( t ) S( t, # ( t )) , |
(12.2) |
|||||||||||
|
|
|
|
|||||||||||||
|
# ( t ) |
N0 |
|
|
|
Г |
|
|
|
|||||||
|
|
d n p( t ) |
|
|
d n 1 p( t ) |
|
Б |
|
|
|
|
|||||
где L( p( t )) an |
|
|
|
an 1 |
|
|
... a0 p( t ) |
– |
линейный |
оператор, |
||||||
|
dtn |
|
dtn 1 |
|||||||||||||
определяемый динамическими свойствамиа(динамикой поведения во време- |
||||||||||||||||
ни) оцениваемого параметра; K |
– парам тр, определяющий усиление в петле |
|||||||||||||||
|
|
|
|
|
|
|
|
к |
|
|
|
|
|
|
|
|
слежения за неизвестным парам тром сигнала; X (t) – комплексная огибаю- |
||||||||||||||||
щая принятой смеси |
|
|
|
е |
|
|
# |
|
|
|
||||||
|
|
|
сигнала и шума; |
S( t , |
) – комплексная оги- |
|||||||||||
бающая полезного сигнала; * – операция комплексного сопряжения; # – обо- |
|||||||||||||
значение соответствующейтценки (значение, используемое в опорном сиг- |
|||||||||||||
нале при приеме). |
|
полезного |
|
|
|
|
|
|
|
||||
Учитывая, что в случае осуществления синхронизации по несущему |
|||||||||||||
|
|
|
и |
|
|
|
|
|
|
|
|
||
колебанию оценке подлежит неэнергетический параметр – фаза колебания, |
|||||||||||||
уравнение для оценки можно преобразовать к виду |
|
|
|||||||||||
Б |
|
л |
|
|
|
|
|
|
|
|
|
||
б |
|
|
|
|
2 |
|
|
|
|
||||
и |
L # ( t ) K |
|
Re X ( t )S* ( t , # ( t )) . |
(12.3) |
|||||||||
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
# ( t ) N0 |
|
|
|
|
||||||
Рассмотрим комплексную огибающую полезного сигнала подробнее. |
|||||||||||||
|
|
|
|
|
|
|
( t )e j ( t ) , |
|
|
|
|||
|
|
|
S( t, ( t )) S |
|
|
|
(12.4) |
||||||
|
|
|
|
|
inf |
|
|
|
|
|
|
||
где Sinf (t) – компонента комплексной огибающей, представляющая инфор-
мационную модуляцию; e j( )t – компонента, определяющая фазу несущего
293
колебания. С учетом этого уравнение для оценки фазы несущего колебания можно переписать так:
|
# |
|
2 |
|
|
# |
* |
|
j # |
( t ) |
|
|
|||
|
L ( t ) K |
|
|
|
Re jX ( t ) S |
inf |
( t ) |
e |
|
|
, |
(12.5) |
|||
|
|
|
|
||||||||||||
|
|
|
N |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
# |
(t) – информационная компонента комплексной огибающей с уче- |
||||||||||||||
где S |
|||||||||||||||
inf |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
том оценки передаваемых информационных символов. |
|
|
|
||||||||||||
Для лучшего понимания полученного результата рассмотрим пример. |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Р |
|
Пусть L # ( t ) |
d |
# ( t ) соответствует отсутствию каких-либо детер- |
|||||||||||||
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
И |
|
минированных проявлений в поведении отслеживаемого процесса (t) во
|
|
|
|
|
|
|
|
|
|
|
|
S( t ) A e j ( t ) |
|
|
|
|
|
|
|
|
|
У |
|
|
|
||||||||||
временной |
области; |
|
соответствует |
сигналу |
|
с BPSK вида |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s( t ) A0 cos( 0t ( t )), тогда имеем |
|
|
|
|
|
Б |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
d |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
( t ) |
|
|
|
|
|
||||||||
|
|
# |
|
|
|
|
|
|
|
|
|
j ( t ) |
|
|
|
|
|
# |
|
# |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j |
|
|
|
|
|
|||||||||
|
|
( t ) |
K |
|
|
|
|
Re j A e |
|
N( t ) |
|
A e |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
dt |
|
|
|
|
|
|
|
|
N0 |
|
|
к |
|
|
Г |
|
|
|
|
|||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
# |
( t ) A# |
|
|
|
# |
( t ) |
|
|
|
||||||||
K |
|
|
|
Re j |
A A# |
e j ( t ) |
N( t )e j |
|
|
(12.6) |
|||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
0 |
0 |
|
|
а |
0 |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
N0 |
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
||||
|
|
|
2K |
|
|
|
|
|
# |
|
|
е |
2 |
|
|
|
|
|
# |
|
|
|
j # ( t ) |
|
|||||||||||
|
|
|
|
A0 |
A0 sin( ( t )) K |
|
|
|
|
Re j |
A0 N( t )e |
|
|
|
|
|
, |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
N0 |
|
|
|
|
о |
|
|
|
N0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
где ( t ) # |
|
и |
|
|
|
|
|
0 |
|
|
|
0 |
|
|
A# |
|
|
|
|
|
|
|
|||||||||||||
( t ) ( t ) |
– |
шибка оценки |
фазы; |
– информационная |
|||||||||||||||||||||||||||||||
компонента опорного колебания на приемной стороне; N( t ) – комплексная
|
|
|
|
б |
|
|
|
|
|
|
2K |
A A# sin( ( t )) – компонента, от- |
||
огибающая шума наблюдения; |
|
|||||||||||||
|
|
и |
лрассогласование |
|
N0 |
|||||||||
ражающая |
|
принимаемого и опорного сигнала; |
||||||||||||
|
|
2 |
|
|
|
|
|
|
# |
|
|
|
|
|
Б |
|
|
|
# |
|
j ( t ) |
|
|
|
|
||||
K |
|
|
|
Re j |
A |
N( t )e |
|
|
– шумовая компонента в схеме оценки фазы |
|||||
|
|
|
||||||||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
N0 |
|
|
|
|
|
|
|
||||||
принимаемого сигнала. В случае когда информационные компоненты принимаемого и опорного сигналов совпадают (информационные модуляции принимаемого и опорного сигналов совпадают), мы имеем
d # |
2K |
2 |
|
2 |
|
|
# |
j # ( t ) |
|
|||
|
( t ) |
|
A |
|
sin( ( t )) K |
|
|
Re j |
A N( t )e |
|
(12.7) |
|
|
|
|
|
|||||||||
|
|
0 |
|
|
|
0 |
|
|
||||
dt |
N0 |
|
|
N0 |
|
|
|
|||||
294

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Р |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
x(t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
|||
|
|
|
|
|
|
|
ФНЧ |
|
|
|
|
|
У |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Г |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Восстановленное |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
несущее |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
колебание |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
/2 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
ГУН |
|
|
|
|
к |
|
|
|
|
|
||||
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
||||
мени равно нулю, |
|
|
|
|
|
|
|
|
|
|
||||||||
|
п л жительной ошибке оценка фазы начинает умень- |
|||||||||||||||||
|
|
|
|
Рис. 12.2. Схема п тли фазовой автоподстройки |
|
|
||||||||||||
|
|
|
|
|
|
соо |
|
|
|
|
|
|
|
|
|
|
||
|
|
Анализ полученных |
ношений показывает, что в отсутствие ошибки |
|||||||||||||||
(ФНЧ – фильтр нижних частот; ГУН – генератор, управляемый напряжением).
синхронизации приращение |
ценки фазы (фазы опорного колебания) во вре- |
|||||||||||||||||
|
|
|
|
|
при |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
величина |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
шаться, при отр цательной ошибке – увеличиваться. При этом скорость из- |
||||||||||||||||||
менения оценки фазы пропорциональна абсолютной величине ошибки. Та- |
||||||||||||||||||
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
ким образом, происходит автоматическое регулирование (синхронизация) |
||||||||||||||||||
и |
|
|
|
|
|
|
|
|
|
|
0 |
0 |
|
|
|
|
||
так, что ы |
|
|
|
|
ошибки ( t ) поддерживалась равной нулю. |
|
||||||||||||
или |
t |
|
2K A2 sin( ( y )) K |
|
2 |
Re j |
|
|
|
# |
( y ) |
|
|
|||||
# ( t ) |
|
|
|
A# N( y )e j |
|
dy . |
(12.8) |
|||||||||||
|
|
N |
|
|
|
N |
|
|
|
|
|
|
|
|
|
|
||
|
0 |
|
|
0 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
Данные соотношения соответствуют алгоритму функционирования |
||||||||||||||||||
классической |
петли фазовой автоподстройки, |
изображенной на |
рис.12.2. |
|||||||||||||||
Нал ч е информационного рассогласования принимаемого и опорного колебан й пр водит к невозможности отслеживания фазы несущего сигнала,
поскольку усреднение во времени величины A A# sin( ( t )) будет вне
зависимости от существующей ошибки синхронизации всегда давать нулевой |
||||
Б |
# |
|
# |
* |
результат. Операция A0 |
A0 |
(в общем случае Sinf( t ) Sinf ( t ) ) по своему |
||
существу является операцией снятия информационной модуляции с принимаемого сигнала.
Точность слежения за фазой определяется характеристиками динамики изменения фазы во времени и интенсивностью шума наблюдения. Вопросам обеспечения требуемых качественных характеристик слежения за фазой при-
295
нимаемого сигнала посвящено большое количество исследований, результаты которых являются отдельным предметом и нами рассматриваться не будут.
12.2.2. Методы синхронизации по несущему сигналу с обратной связью по решению
Как было показано выше, на процесс синхронизации по фазе несущего
колебания существенное влияние оказывает согласование принимаемого |
|
сигнала и опорного колебания по информационной модуляции. |
Р |
|
|
Правильное снятие информационной модуляции с принимаемого сиг- |
|
И |
|
нала может быть осуществлено путем использования результатов (выходных |
|
сигналов) непосредственно демодулятора. При этом необходимо иметь в виду, что решение о передаваемых символах в процессе демодуляции принимается с запаздыванием на длительность данных символов. То есть решение принимается в конце интервала передачи конкретного символа (когда реше-
ние уже есть во входном сигнале, уже нет данного символа). В связи с этим |
||
|
|
У |
для правильного информационного согласования принимаемого и опорного |
||
|
Г |
|
сигналов в схеме оценки частоты и фазы несущего колебания должна ис- |
||
пользоваться копия входной смеси сигн |
и шума, задержанная на время за- |
|
|
Б |
|
паздывания решения в демодуляторе. Следует отметить, что существенным |
||
ла условием нормального функционировкния д нного решения синхронизации
по фазе несущего колебания являются медленные изменения фазы несущего колебания по сравнению со скоростью информационной модуляции (за вре-
мя, соответствующее длительности информационного символа, фаза практи- |
|||
|
|
|
е |
чески не изменяется). С рук урная схема блока оценки частоты и фазы не- |
|||
сущего колебания с бра н й связью по решению приведена на рис. 12.3. |
|||
|
|
т |
|
12.2.3. |
о |
|
|
Методы синхронизации по несущему колебанию, |
|||
не управ яемые решением |
|||
|
и |
|
|
Вместолиспользования схемы, управляемой решениями для получения |
|||
оценки фазыб, можно трактовать передаваемые данные как случайные величины просто усреднить функцию правдоподобия по этим случайным вели-
Бчинами, а затем искать ее максимум. Чтобы выполнить такое усреднение, можно использовать или действительную функцию распределения вероятностей данных, если она известна, или можно предположить некоторое распределение вероятностей, которое является подходящим приближением для правильного распределения. Следует отметить, что в результате подобного усреднения вообще может пропасть информация о фазе несущего сигнала, так что подобная методика не является универсальной для большинства модуляционных схем.
296
|
|
x(t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X( )t |
|
|
|
|
|
X ( t )e j # |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
Квадратурный |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
преобразователь |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Демодулятор |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
частоты |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e j # |
|
|
|
|
|
|
|
|
|
с |
|
|
|
|
|
|
|
|
|
|
|
|
Р |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
Вычислитель |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
||||||||||||
|
|
|
|
|
|
|
e j # |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S # |
(t) * |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
inf |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Демодулированные |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Модулятор |
|
|
|
|
символы |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Г |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Схема оценки частоты |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и фазы несущего |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
колебания |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
||||
Рис. 12.3. Синхронизация по |
|
|
|
|
|
|
|
|
|
|
олеб нию с обратной связью |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
по р ш нию |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
к |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Наряду с методами восс ановл ния фазы несущего колебания, осно- |
||||||||||||||||||||||||||||||||
ванными на усреднении |
|
|
|
|
несущему |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
ансамблю передаваемых информационных сим- |
|||||||||||||||||||||||||||||||
волов, широкое распр с ранение получили «полуэвристические» методы,
основанные на |
|
|
|
вании свойств симметрии сигнальных созвездий не- |
|||||||||
|
|
|
|
|
|
|
т |
|
|
|
|
||
которых модуляц онных схем. Рассмотрим их более подробно. |
|
||||||||||||
|
|
|
|
по |
|
|
|
|
|
||||
|
|
использ |
|
|
|
|
|
|
|
||||
12.2.3.1. Синхронизация при приеме сигнала с /2-BPSK |
|
||||||||||||
|
л |
|
|
|
|
|
|
|
|
|
|
||
Комплексная огибающая сигнала с произвольной бинарной фазовой |
|||||||||||||
|
б |
|
|
|
|
|
|
|
|
|
|
||
ман пуляц ей полностью определяется его квадратурной и синфазной ком- |
|||||||||||||
понентамии представляется следующим выражением: |
|
||||||||||||
|
|
|
|
|
|
jCk |
|
|
|
) cos C |
j sin C . |
|
|
S( t ) A g |
|
( t k |
|
)e |
A |
g |
( t k |
(12.9) |
|||||
|
|
|
|
||||||||||
Б |
0 k 0 |
F |
|
b |
|
|
|
0 k 0 F |
b |
k |
k |
|
|
Слежение за фазой несущего колебания в случае, когда используемая девиация фазы отлична от величины /2, не представляет сложности. Данное слежение осуществимо обычной петлей фазовой автоподстройки, поскольку модулированный сигнал содержит немодулированную компоненту, представляющую несущее колебание cos Ck cos( ) const . В случае ко-
297
гда / 2 , данная компонента пропадает, что требует осуществления специальных мер по снятию информационной модуляции. Рассмотрим два наиболее «популярных» способа осуществления данной процедуры.
При /2-BPSK комплексная огибающая для любого шага модуляции записывается следующим образом:
|
jCk |
|
|
|
|
jA C . |
(12.10) |
||
S( t ) A e |
|
2 |
||
0 |
|
|
0 k |
|
Напомним, что Ck 1, при этом знак определяется модулирующими сим- |
||||||||||
волами. |
|
|
|
|
|
|
|
|
Р |
|
|
|
|
|
|
|
|
|
|
|
|
С учетом неизвестной фазы несущего колебания имеем |
|
|
||||||||
|
|
|
|
|
|
|
|
И |
|
|
|
|
jCk |
|
|
|
|
У |
|
|
|
S( t ) |
|
A e |
|
2 e j ( t ) jA C e j ( t ) . |
|
|
(12.11) |
|||
|
|
0 |
|
|
|
0 k |
|
|
|
|
Возведем комплексную огибающую в квадрат: |
|
|
|
|
||||||
|
2 |
|
jC |
|
Б |
|
|
|
|
|
2 |
j2 ( t ) |
2 j2 ( t ) |
|
|
(12.12) |
|||||
S( t ) |
A e |
|
k |
e |
A eГ. |
|
|
|||
|
|
0 |
|
пок |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Анализ полученного выражения |
зыв ет, что квадрат комплексной |
|||||||||
огибающей сигнала с /2-BPSK свободен от модуляции информационными |
||||||||||
|
|
е |
|
|
|
|
|
|||
символами и содержит информацию обаудвоенной фазе несущего колебания,
которая может быть отслежена п тл й фазовой автоподстройки (способ реализуется так называемой схемой Сифорова):
|
|
|
|
о |
|
|
|
|
|
|
|
|
|||
|
d |
# |
|
|
|
2 |
|
|
2 j 2 ( t ) 2 |
# |
|
|
|
||
|
|
|
|
|
|
|
|
|
0 |
|
0 |
|
|
|
|
2 |
|
|
( t ) K |
|
|
Re |
j A e |
|
A e |
|
|
. |
(12.13) |
||
|
dt |
|
и |
N |
|
|
|
|
|
|
|
|
|
||
|
|
л |
|
|
т0 |
|
|
|
|
|
|
||||
При записи последнего выражения были опущены шумовые компонен-
смесиимодулированногоб радиосигнала и шума в квадрат.
ты, опреде яемые результатом возведения комплексной огибающей входной
Второй способ использует идентичность информационной модуляции синфазной квадратурной компонент сигнала с /2-BPSK. Запишем комплексную огибающую принятого сигнала с учетом ее коррекции оценкой фа-
зы несущей # ( t ):
Б |
|
|
# |
( t ) |
|
S( t ) jA C |
e j ( t ) j |
|
|||
|
0 |
k |
|
|
|
|
A0 jCk cos( ( t ) # ( t )) Ck sin( ( t ) # ( t )) , |
(12.14) |
|||
|
|
SI ( t ) A0Ck sin( ( t )) , |
(12.15) |
||
298
SQ( t ) A0Ck cos( ( t )) , |
(12.16) |
( t ) # ( t ) ( t ) . |
(12.17) |
Произведение квадратурных компонент дает следующий результат:
S |
( t )S |
Q |
( t ) A2 |
C |
k |
2 sin( ( t ))cos( ( t )) |
A02 |
sin( 2 ( t )) . |
(12.18) |
|
|||||||||
I |
|
0 |
|
2 |
|
|
|||
|
|
|
|
|
|
|
|
||
В этом случае также происходит съем информационной модуляции, а результат перемножения содержит информацию об удвоенной фазе (или ошибке отслеживания фазы) несущего колебания, которая может отслежи-
ваться |
обычной |
петлей фазовой автоподстройки (способ |
реализуется так |
|||||||||||||||||
называемой схемой Костаса). |
|
|
|
|
|
|
|
|
|
|
Р |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
Следует заметить, что схемы Костаса и Сифорова идентичны, посколь- |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
|
ку в обеих схемах в основе оценки фазы лежит результат перемножения син- |
||||||||||||||||||||
фазной и квадратурной компонент принятого сигнала. |
У |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Структурные схемы Сифорова и Костаса, реализованные в области ну- |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Г |
|
|
|
левой и радиочастот, приведены на рис. 12.4 и 12.5 соответственно. |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
12.2.3.2. Синхронизация при приеме сигнала с M-PSK |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
||
|
Комплексная огибающая сигналакна интервале действия одного ин- |
|||||||||||||||||||
формационного символа в случае сигнала с M-PSK определяется следующим |
||||||||||||||||||||
образом: |
|
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S( t ) A e j m |
, |
|
|
|
(12.19) |
||||||
|
|
|
|
|
|
|
|
|
т |
0 |
|
|
|
|
|
|
|
|
||
|
|
|
|
2 ( m 1) |
|
о |
|
|
|
|
|
|
|
|
|
|
|
|||
где |
|
|
– разрешенные фазовые состояния сигнала представля- |
|||||||||||||||||
m |
|
|||||||||||||||||||
|
|
|
|
M |
и |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ющие различные информационные символы; m 1,...M . |
|
|
|
|||||||||||||||||
|
|
|
|
|
л |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
С учетом неизвестной фазы несущего колебания имеем |
|
|
|||||||||||||||||
|
|
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
и |
|
|
|
|
|
j |
2 ( m 1 ) |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
M |
|
e |
j ( t ) |
. |
|
|
(12.20) |
|||||||||
|
|
|
|
|
|
|
|
|||||||||||||
Б |
|
|
|
|
|
S( t ) A0e |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
299

|
x(t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
# |
|
|
|
|
|
|
Квадратурный |
X ( t ) |
|
|
X ( t )e j |
|
|
|
|
|
|||||
|
преобразователь |
|
|
|
|
|
|
|
Демодулятор |
|
|||||
|
|
частоты |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Х |
|
|
|
|
|
|
Схема Сифорова |
Р |
||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
e j # |
|
|
2 |
j2 # |
|
|
|
|
|||
|
|
|
|
|
|
|
|
Х |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вычислитель |
|
|
|
|
|
И |
||||
|
|
|
|
|
|
e j # |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
У |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
Г |
|
|
|
|
x(t) |
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
X( )t |
|
|
|
а |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
# |
|
|
|
|
|
|
|
Квадратурный |
|
|
|
|
X ( t )e j |
|
|
|
|
|
|
|||
|
|
|
|
|
к |
|
|
|
|
|
|
||||
|
преобразователь |
|
|
|
|
|
Демодулятор |
|
|||||||
|
|
частоты |
|
|
|
е |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
тRe{.} |
|
Im{.} |
|
|
|
|
||||
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
||
|
|
|
и |
|
|
|
|
|
|
|
Схема Костаса |
|
|||
|
|
л |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
б |
|
|
Вычислитель |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
и |
|
|
|
|
e |
j # |
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 12.4. Компенсация фазы несущего колебания при приеме сигнала |
|||||||||||||||
|
|
|
|
|
|
|
|
с /2-BPSK |
|
|
|
|
|
||
300

x(t) |
Х2 |
|
ФНЧ |
|
Схема Сифорова
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ГУН |
|
|
|
|
|
Р |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
/2 |
|
|
|
|
|
|
|
f |
|
|
|
|
Восстановленное |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
несущее колебание |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f/2 |
|
У |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Г |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
ФНЧ |
|
к |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
|
|
|
Восстановленное |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
несущее колебание |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
/2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
x(t) |
|
|
|
|
|
о |
|
|
Схема Костаса |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
и |
ГУН |
|
|
|
|
ФНЧ |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
л |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
и |
|
|
|
|
|
|
ФНЧ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Р с. 12.5. Восстановление несущего колебания при приеме сигнала |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
с /2-BPSK |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Возведем комплексную огибающую в M -ю степень: |
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S( t ) M AM e j2 ( m 1)e jM ( t ) AM e jM ( t ) . |
|
|
(12.21) |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
301
Таким образом, M-я степень комплексной огибающей сигнала с M-PSK свободна от модуляции информационными символами и содержит информацию о фазе несущего колебания, которая может быть отслежена петлей фазовой автоподстройки (обобщенная на случай многопозиционной фазовой манипуляции схема Сифорова). Выражение, описывающее работу данной схемы, записано ниже (шумовые компоненты при записи опущены):
|
d |
# |
2 |
|
M |
jM ( t ) M |
# |
|
|
|
||
|
|
|
jM |
( t ) |
|
|
||||||
|
|
|
|
0 |
|
0 |
|
|
|
|
||
M |
|
( t ) K |
|
|
Re |
j A e |
|
A e |
|
|
. |
(12.22) |
|
dt |
|
N0 |
|
|
|
|
|
|
|
||
|
|
На рис. 12.6 изображены структурные схемы слежения за фазой несу- |
||||||||||
щего колебания при приеме сигналов с многопозиционной фазовой манипу-
ляцией для случаев обработки на радиочастоте и в области нулевой частоты. |
|
|
Р |
И |
|
12.2.3.3. Синхронизация при приеме сигнала с QPSK и OQPSK |
|
У |
|
Сигналы с квадратурной фазовой манипуляцией по своей сути являют- |
|
ся частным случаем многопозиционной фазовойГманипуляции M-PSK |
|
(M = 4). Для восстановления несущего колебания при их приеме возможно |
|
использование обобщенной схемы |
Б. В качестве альтернативного |
варианта слежения за изменениями ф зы несущего колебания может быть
использован |
|
вариант |
схемы Костаса, расширенный на прием сигналов |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
Сифорова |
|
с 4-позиционной фазовой манипуляци й. Рассмотрим его подробнее. |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
к |
|
Комплексная огибающая принятого сигнала с учетом ее коррекции |
||||||||||||
оценкой фазы несущей # (t) дляесигналов с QPSK и OQPSK записывается |
||||||||||||
следующим образом: |
|
|
т |
|
|
|||||||
S( t ) A C |
|
jC |
|
|
|
|
|
|
|
|||
I |
Q |
e j ( t ) j # ( t ) |
|
|
||||||||
|
0 |
|
|
|
о |
|
|
|||||
|
|
|
|
и |
|
|
|
|
||||
A0 CI cos( ( t )) CQ sin( ( t )) j CQ cos( ( t )) CI sin( ( t )) , |
(12.23) |
|||||||||||
|
|
л |
|
C |
|
cos( ( t )) C sin( ( t )) , |
|
|||||
|
|
S ( t ) A |
I |
(12.24) |
||||||||
|
бI |
|
|
0 |
|
|
Q |
|
||||
и |
SQ( t ) A0 CQ cos( ( t )) CI sin( ( t )) , |
(12.25) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
||
Б |
|
|
|
|
|
|
|
|
|
|
|
|
CI ;CQ 1.
302

x(t) |
ХM |
|
|
|
ФНЧ |
ГУН
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Р |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
|
|
|
|
|
|
Восстановленное |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
/2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
несущее колебание |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f/M |
|
|
|
И |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
x(t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Г |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X (t) |
|
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
# |
Б |
|
|
|
|
|||||||||||||||
|
|
Квадратурный |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X ( t )e j |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
преобразователь |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
к |
|
|
|
|
|
|
Демодулятор |
|
|
||||||||||||||||
|
|
|
|
|
|
|
M |
|
|
е |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
частоты |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
Х |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
л |
e |
j # |
|
|
|
|
|
|
Х |
M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Б |
б |
|
|
|
|
Вычислитель |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
e j # |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
Рис. 12.6. Обобщенная схема Сифорова |
|
|
|
||||||||||||||||||||||||||||||||||
|
|
Рассмотрим |
|
|
/4-окрестность |
нулевой |
|
|
ошибки синхронизации |
||||||||||||||||||||||||||||||||||
( 0 ). В данной окрестности знак синфазной составляющей SI ( t ) будет определяться знаком символа CI , а знак квадратурной компоненты
303
SQ ( t ) – знаком символа CQ или, с другой стороны, выполняются следующие
равенства: |
|
|
|
|
|
|
|
|
|
CI sign SI ( t ) , |
|
|
|
|
|
(12.28) |
|
|
CQ sign SQ( t ) . |
|
|
|
|
|
(12.29) |
|
Выполнив перемножения следующего вида, получим |
|
|
Р |
|||||
SI ( t )sign( SQ( t )) A0 CI CQ cos( ( t )) sin( ( t )) |
|
|||||||
, |
|
(12.30) |
||||||
SQ( t )sign( SI ( t )) A0 CI CQ cos( ( t )) sin( ( t )) . |
|
|
(12.31) |
|||||
|
|
|
|
У |
|
|
|
|
В результате окончательная операция снятия информационной моду- |
||||||||
|
|
|
Г |
И |
|
|||
ляции может быть определена следующим образом: |
|
|
||||||
|
|
|
Б |
|
|
|
|
|
SI ( t )sign( SQ( t )) SQ( t )sign( SI ( t )) 2A0 sin ( t ) . |
|
(12.32) |
||||||
Соответствующие структурные схемы приведены на рис. 12.7. |
|
|||||||
|
|
к |
|
|
|
|
|
|
12.2.3.4. Синхронизация при априеме сигнала с QAM |
|
|
||||||
|
т |
|
|
|
|
|
|
|
В качестве примера рассмотрим синхронизацию по фазе несущего ко- |
||||||||
лебания сигнала 16-QAM c квадраеным созвездием сигнала, изображенным |
||||||||
о |
|
|
|
|
|
|
|
|
на рис. 12.8. Как видно из рисунка, сигнальное созвездие содержит три груп- |
||||||||
и |
|
|
|
|
|
|
|
|
пы точек, расположенных на перпендикулярных прямых. Первая группа то-
чек 0000, 0101, 1111, 1010, 0010, 0111, 1101, 1000; вторая 0100, 1110, 0011, 1001 и третьял0001, 1011, 0110, 1100. При последовательном осуществлении
получ тся с гнальное созвездие, содержащее только три точки (рис. 12.9). БНа р сунке цифры, которыми помечены сигнальные точки, соответствуют группам точек исходного созвездия.
амплитудного огран чен я в пределах приведенной окружности и возведении в четвертуюб степень ограниченного сигнала, каждая из групп точек преобразуетсяив одну. Таким образом, вместо сигнального созвездия из 16 точек
При равной вероятности появления символов в исходном сигнале вероятность появления сигнала, соответствующего точке 1, будет в два раза превосходить вероятность появления каждого из оставшихся двух сигналов (точки 2 и 3).
304

|
|
|
|
|
|
|
|
Q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
ФНЧ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
_ |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x(t) |
|
|
|
|
/2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
ГУН |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ФНЧ |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
I |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Р |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
ФНЧ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
|
|
|
|
||||||||||
|
|
x(t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Г |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
# |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
Квадратурный |
X (t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
X ( t )e j |
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
преобразователь |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Демодулятор |
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
к |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
частоты |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Re{.} |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Im{.} |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
о |
т |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sign(.) |
|
|
|
|
|
sign(.) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
_ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
л |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Б |
|
|
|
|
|
|
|
|
|
e |
# |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
Вычислитель |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 12.7. Схема Костаса для случая приема сигналов с QPSK и OQPSK
Указанные выше два последовательных преобразования уже позволяют отслеживать фазовые изменения несущего колебания с использованием схемы фазовой автоподстройки. При этом значение отслеживаемой фазы будет
305
соответствовать фазовому положению точки 1. Следует отметить, что две оставшиеся точки можно рассматривать как сигнал с BPSK (девиация фазы отлична от /2), при этом немодулированная компонента данного сигнала (несущее колебание) находится в противофазе сигнальной точке 1, что приводит к неоправданным потерям энергии сигнала и ухудшению помехоустойчивости процесса слежения за фазой. Для исключения данного обстоятельства целесообразно преобразованный сигнал подвергнуть делению частоты на четыре. В результате данного деления частоты созвездие преобразованного сигнала приобретет вид, приведенный на рис.12.10.
У сигнала с созвездием, соответствующим изображенному на рис. 12.10, практически вся энергия сосредоточена в спектральных компонентах
совпадающих по фазе с первой точкой. |
|
Р |
12.1.1.1. Заключительные замечания |
|
|
|
И |
|
|
|
|
В заключение необходимо отметить, что приведенные выше методы |
||
синхронизации по фазе несущего колебания обладаютУсущественным недо- |
||
|
Г |
|
|
Б |
|
статком. Данный недостаток заключается в том, что синхронизация осу-
ществляется с точностью до постоянных заранее определенных фазовых углов. Например, для сигнала с QPSK д нные ф зовые ошибки могут состав-
лять /2 и . Это может приводить |
явлению так называемой обратной ра- |
|||||||||
боты, описанному ранее. |
Методы борьбы с обратной работой известны и |
|||||||||
здесь не рассматривались. |
|
|
|
а |
|
|||||
|
|
к |
|
|||||||
|
|
|
0000 |
|
е |
|
|
|
||
|
|
|
|
|
|
|
||||
|
|
|
т |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
и0001 |
|
|
|
|
|
|
|
|
|
л |
|
|
|
|
|
|
|
|
|
б |
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
|
|
|
|
|
|
0010 |
|
0110 |
|
|
|
||
|
|
|
|
1110 |
1010 |
|||||
|
|
|
Рис. 12.8. Сигнальное созвездие 16-QAM |
|||||||
306
3
1
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
Р |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
||
Рис. 12.9. Сигнальное созвездие 16-QAM после ограничения и возведения |
||||||||||||||||
|
|
|
|
|
|
в четвертую степень |
|
У |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
Г |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
к |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
е |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
о |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
л |
|
|
|
|
|
|
|
|
|
|
|
|
||
Р с. 12.10. Сигнальное созвездие преобразованного сигнала 16-QAM |
||||||||||||||||
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
и |
|
|
|
|
после деления частоты |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
12.2. Методы восстановления тактовой синхронизации |
|
|
||||||||||||||
Б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В цифровой системе связи выход демодулятора должен периодически стробироваться со скоростью передачи символов в точно выбранных моментах tm m c , где c – длительность модулирующего символа, а – но-
минальное время задержки, которое определяется временем распространения сигнала от передатчика к приѐмнику. Чтобы выполнять это периодическое
307
стробирование, требуется синхронизирующий сигнал в приемнике. Процесс получения такого сигнала в приѐмнике обычно называется тактовой синхронизацией (синхронизацией символов), или восстановлением отсчѐтов времени.
Восстановление отсчѐтов времени – одна из наиболее ответственных функций, которые выполняются в приѐмнике цифровых систем связи. Отметим, что приѐмник должен знать не только частоту ( 1 / c ) , с которой стро-
бируются выходы согласованных фильтров или корреляторов, но также тот момент времени, в который необходимо взять отсчѐты внутри каждого сим-
вольного интервала. Положение отсчѐтного момента внутри символьного ин-
связи синхрогенераторы передатчика и приѐмника синхронизированыРпо образцовому таймеру, который обеспечивает высокостабильную сетку време-
тервала длительностью c называют фазой синхронизации. Тактовую син-
хронизацию можно выполнить несколькими путями. В некоторых системах
новременной передаче передатчиком опорной частоты, равной или кратной
ни (например, системы GPS, CdmaOne, CDMA2000 и UMTS). В этом случае |
||
приѐмник должен оценить и скомпенсировать только относительноеИ |
время |
|
задержки между переданным и принятыми сигналом. |
У |
|
|
|
|
Другой метод для достижения синхронизации символов заключается в од- |
||
Г |
|
|
|
|
на |
|
||
1 / c , вместе с информационным сигналом. Приѐмник может просто использо- |
|||||
вать узкополосный фильтр, настроенный |
|
переданнуюБ |
опорную частоту, и |
||
|
датчик |
|
|
||
таким образом извлечь синхронизирующий сигнал для стробирования. Этот |
|||||
Здесь |
|
|
|
|
|
подход прост для применения. |
имеется, однако, |
несколько неудобств. |
|||
Первое заключается в том, что п р |
|
|
должен отдать некоторую часть воз- |
||
тод часто используется втсис емах телефонной связи, которые используют большие полосы ичаст т для передачи сигналов многих пользователей. В таком случае затратылна передачу синхронизирующего сигнала делятся на многих пользовате ей. Посредством такого деления потери в мощности передатчика и полосебчастот уменьшаются пропорционально числу пользователей.
можной мощности для передачи опорного сигнала. Другое заключается в том,
что некоторая малая час ь дос упной в канале полосы частот должна быть занята для передачи опорного сигнала. Несмотря на эти неудобства, этот ме-
иСинхронизирующий сигнал можно также извлечь из принимаемого информац онного сигнала. Имеется определѐнное число различных методов, Бкоторые можно использовать в приѐмнике, чтобы достичь самосинхронизации. В этом разделе мы обсудим как метод оценивания, управляемого решениями, так и метод оценивания, не управляемого решениями.
12.2.1. Тактовая синхронизация, управляемая решением
Обобщенное правило формирования текущей оценки времени запаздывания сигнала для случая его наблюдения на фоне белого гауссовского шума в установившемся режиме определяется следующим образом (данное правило справедливо для оценки любого параметра сигнала и уже нами использо-
308
валось при рассмотрении методов синхронизации по фазе несущего колебания):
|
|
|
1 |
|
|
|
|
* |
|
|
|
L # ( t ) K |
|
X ( t ) S( t , # ( t )) X ( t ) S( t, # ( t )) |
, |
(12.33) |
|||||||
|
|
||||||||||
|
# ( t ) |
N0 |
|
|
|
|
|
|
|
||
поскольку время запаздывания сигнала является неэнергетическим параметром, уравнение для оценки можно преобразовать к виду
|
|
|
2 |
|
|
|
|
|
L # ( t ) K |
|
Re X ( t )S* ( t , # ( t )) . |
(12.34) |
|||||
|
|
|||||||
|
|
|
|
|
|
|
||
|
# ( t ) N0 |
|
|
|
|
|||
Рассмотрим комплексную огибающую полезного сигнала (для просто- |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Р |
|
ты будем рассматривать только методы линейной модуляции – PSK, QAM и |
||||||||||||||||||||||||
др.). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( t )e j ( t , ) . |
У |
|
||||||||
|
|
|
|
|
S( t, ( t, ), ) S |
(12.35) |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
inf |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Г |
|
|
||
В общем случае фаза несущего колебания зависит от времени запазды- |
||||||||||||||||||||||||
вания. |
Мы будем считать, что синхрониз ция по фазе несущего колебания |
|||||||||||||||||||||||
уже осуществлена. В этом случае |
|
|
|
|
|
|
Б |
|
|
|
||||||||||||||
|
|
|
|
|
я огибающая имеет вид |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
||||
|
|
|
|
|
|
|
|
S( t ) Sinf |
|
|
|
(12.36) |
||||||||||||
|
|
|
|
|
|
|
|
( t ). |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
комплексн |
|
|
|
|
|
|
|||||
С учетом этого имеем сл дующ |
|
уравнение для оценки времени за- |
||||||||||||||||||||||
паздывания сигнала: |
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
т2 |
|
|
|
|
|
|
|
|
|
|||||||
|
|
L # ( t ) |
K |
|
|
|
|
|
|
|
|
Re X cor ( t )S* |
|
( t # ( t )) |
, |
(12.37) |
||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
# |
N |
|
|
|
|
|
|
inf |
|
|
|
||||||
|
|
|
|
|
о |
|
0 |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
( t ) |
|
|
|
|
|
|
|
|
|
|
|||||||
cor |
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
( t ) – резу ьтат коррекции принятой смеси полезного сигнала и шу- |
||||||||||||||||||||||||
где X |
|
|||||||||||||||||||||||
|
|
|
л |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ма с учетом с нхронизации по фазе несущего колебания. |
|
|
||||||||||||||||||||||
Структурнаяб |
схема, реализующая полученное уравнение для оценки |
|||||||||||||||||||||||
времени запаздывания сигнала, приведена на рис. 12.11. |
|
|
|
|||||||||||||||||||||
Снятие |
информационной |
|
|
модуляции с |
|
принимаемого |
сигнала осу- |
|||||||||||||||||
ществляетсяБ результатами демодуляции информационных символов. Поскольку решение о значении передаваемых символов в процессе демодуляции принимается с запаздыванием на длительность данных символов, в цепи тактовой синхронизации используется скорректированная копия смеси сигнала и шума, задержанная на длительность информационного символа.
309
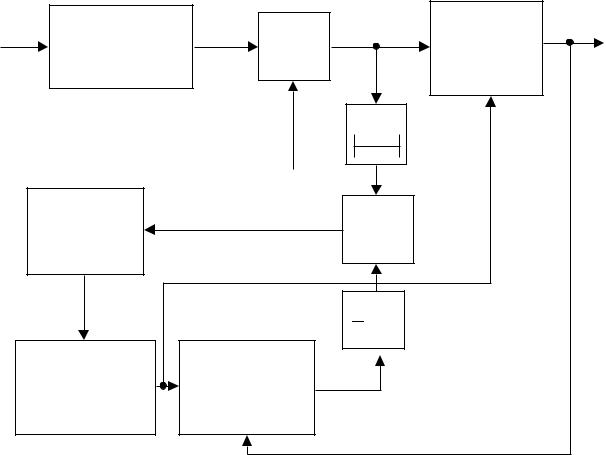
12.2.2.Тактовая синхронизация, неуправляемая решением
|
Оценка параметров задержки принимаемого сигнала, неуправляемая |
|||||||||||||||||||
решением, возможна путем усреднения функции правдоподобия с учетом ве- |
||||||||||||||||||||
роятностных характеристик передаваемых символов. |
|
|
|
|
||||||||||||||||
|
Среди устройств тактовой синхронизации, не управляемых решением, |
|||||||||||||||||||
наиболее широкое распространение получили нелинейные синхронизаторы. |
||||||||||||||||||||
Поскольку в спектре радиосигнала, как правило, отсутствуют частотные |
||||||||||||||||||||
компоненты, |
|
представляющие |
|
необходимую |
тактовую |
синхро- |
||||||||||||||
последовательность, устройства синхронизации этого класса генерируют |
||||||||||||||||||||
данные компоненты, пропуская поступающий низкочастотный сигнал (сиг- |
||||||||||||||||||||
нал после квадратурного преобразования частоты) через последовательность |
||||||||||||||||||||
фильтра и нелинейного устройства. На рис. 12.12 приведены три примера не- |
||||||||||||||||||||
линейных тактовых синхронизаторов. |
|
|
|
|
|
|
|
|
|
Р |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
X ( t ) |
|
|
|
|
X cor ( t ) |
|
И |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
|
|
|||||
x(t) |
|
Квадратурный |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
преобразователь |
|
|
|
|
|
|
|
Демодулятор |
|
|||||||||
|
|
|
частоты |
|
|
|
|
|
|
|
|
|
Г |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
e j # ( t ) |
|
а |
с |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
к |
|
|
|
|
|
|
|
|
|||
|
Вычислитель |
|
|
е |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
т |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
# |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
о |
|
|
|
|
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
(.) |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
Генератор |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
л |
|
Модулятор |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
тактовых |
|
|
|
|
|
* |
|
|
|
|
|
|
|
|
||||
|
|
мпульсов |
|
|
|
|
|
|
|
|
|
# |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
Sinf (t |
|
(t)) |
|
|
|
|
|||||
|
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Оценки принятых |
|||||
|
|
|
|
|
|
|
|
|
|
|
информационных символов |
|||||||||
Б |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Рис. 12.11. Тактовая синхронизация с обратной связью по решению |
||||||||||||||||||||
В первом примере поступающий сигнал фильтруется с использованием согласованного формирующим импульсом gF ( t ) фильтра. Выходной сигнал этого фильтра представляет собой автокорреляционную функцию импульса gF ( t ). Например, при передаче с помощью прямоугольных формирующих
310
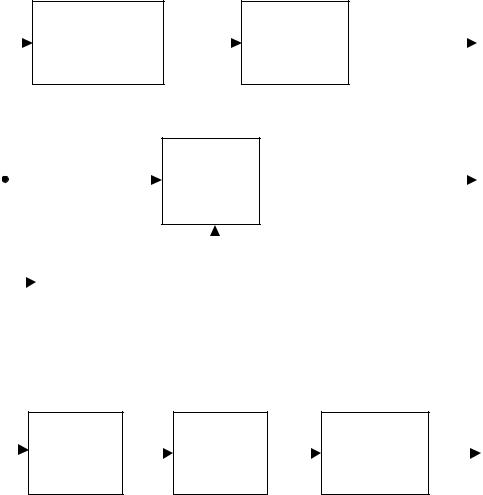
импульсов на выходе будем иметь треугольный сигнал. Затем полученная последовательность автокорреляционных импульсов выпрямляется с помощью некоторой нелинейности четного порядка, например квадратичного устройства или устройства взятия модуля. Полученный таким образом сигнал будет содержать пики положительной амплитуды, которые с точностью до временной задержки соответствуют переходам входных символов. Таким образом, сигнал с выхода нелинейности будет содержать компоненту на требуемой частоте и с требуемой фазой тактового генератора. Данная частотная составляющая может быть использована для формирования синхронизированного тактового сигнала.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
|||
|
|
|
|
|
|
|
Согласованный |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
синхронизации |
||||||||
|
|
|
|
|
|
|
|
|
с gF(t) |
|
|
|
|
|
|
|
| . | |
|
|
|
|
|
|
|
Р |
|||||||
|
|
|
|
|
|
|
|
|
фильтр |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Г |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
тактовой |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
сигнала |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
формированияи |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
c/2 |
|
|
|
|
|
|
т |
к |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
выделения |
|||||
|
|
|
|
|
|
|
|
|
л |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| . | |
|
|
|
|
|
устройству |
|||
|
|
|
|
|
|
|
ФНЧ |
|
|
|
|
d/dt |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
к |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 12.12. Нелинейные тактовые синхронизаторы
Во втором примере (рис. 12.12) компонента на тактовой частоте создается посредством задержки и умножения. Длительность задержки равна половине периода передачи символа, и это значение является оптимальным, поскольку оно обеспечивает наибольшую амплитуду получаемой синхронизирующей составляющей. Как и ранее, нужная спектральная компонента мо-
311
жет быть использована для формирования синхронизированного тактового сигнала.
Последний пример соответствует контурному детектору. Основными операциями здесь являются дифференцирование и выпрямление (посредством использования квадратичного устройства). Если на вход поступает сигнал прямоугольной формы, дифференциатор дает положительные или отрицательные пики на всех переходах символов. При выпрямлении получаемая последовательность положительных импульсов будет формировать Фурье-компоненту, соответствующую тактовой синхронизации символов.
Потенциальной проблемой данной схемы является то, что дифференциаторы обычно весьма чувствительны к широкополосному шуму. Это делает необходимым введение перед дифференциатором фильтра нижних частот, как показано на рис. 12.12.
|
|
|
|
Р |
12.3. Кадровая синхронизация |
|
|
И |
|
|
|
|
||
Практически все потоки цифровых данных имеют некоторую кадровую |
||||
|
|
У |
|
|
структуру. Другими словами поток данных разбит на равные группы симво- |
||||
|
Г |
|
|
|
|
Б |
|
|
|
лов. Если поток данных – это оцифрованный телесигнал, каждый пиксел в |
||||
нем представляется словом из нескольких бит, которые группируются в горизонтальные растровые развертки, з тем в вертикальные растровые раз-
вертки. Компьютерные данные обычно р збив ются на слова, состоящие из |
|
|
а |
некоторого числа 8-битовых байт, оторые, в свою очередь, группируются в |
|
пакеты, кадры или файлы. Любая систкма, использующая кодирование с за- |
|
щитой от блочных ошибок, в кач |
основы кадра должна брать длину ко- |
стве |
|
т |
|
дового слова. Оцифрованная речь обычно передается пакетами или кадрами, |
|
неотличимыми от других цифровых данных. |
|
должен синхрон з роваться с кадровой структурой потока данных. Кадровая синхронизация обычно выполняется с помощью некоторой специальной
Чтобы входной п т к данных имел смысл для приемника, приемник
процедуры передатчика. Данная процедура может быть как простой, так и |
|||
|
|
|
и |
довольно с ожной, в зависимости от среды, в которой должна функциониро- |
|||
вать системал. |
|||
|
Простейшим методом, используемым для облегчения кадровой син- |
||
|
|
б |
|
хрон зац , является введение маркера. Маркер кадра – это отдельный сим- |
|||
вол |
|
краткая последовательность символов, периодически вводимая пере- |
|
|
или |
|
|
Б |
|
|
|
датчиком в поток данных. Приемник должен знать эту последовательность и период ее введения. Приемник, достигший синхронизации данных, сопоставляет (проверяет корреляцию) эту известную последовательность с потоком поступающих данных в течение известного периода введения. Если приемник не синхронизирован с кадровой последовательностью, корреляция будет слабой. При синхронизации приемника с кадровой структурой корреляция будет практически идеальной, повредить которую может только случайная ошибка детектирования.
312
Преимуществом маркера кадра является его простота. Для маркера может быть достаточно даже одного символа, если перед принятием решения, находится ли система в состоянии кадровой синхронизации, было выполнено достаточное число корреляций. Основной недостаток состоит в том, что данное достаточное число может быть очень большим; следовательно, большим может быть и время, требуемое для достижения синхронизации. Таким образом, наибольшую пользу маркеры кадров представляют в системах, непрерывно передающих данные, подобно многим телефонным и компьютерным каналам связи, и не подходят для систем, передающих отдельные
пакеты, или систем, требующих быстрого получения кадровой синхронизации. Еще одним недостатком маркера кадра является то, что введенный символ (символы) может повысить громоздкость структуры потока данных.
системах с необходимостью быстрого получения синхронизации рекомендуР - ется использовать синхронизирующие кодовые слова. Обычно такие кодовые
слова передаются как часть заголовка сообщения. ПриемникИдолжен знать кодовое слово и постоянно искать его в потоке данных, возможно, используя
В системах с неустойчивыми или пульсирующими передачами либо в
для этого коррелятор на согласованных фильтрах. ДетектированиеГУ кодового слова укажет известную позицию (обычно – начало) информационного кадра. Преимуществом подобной системы является то, что кадровая синхрони-
зация может достигаться практически мгновенно. Единственная задержка – |
||
отслеживание кодового слова. Недост |
|
Б |
– кодовое слово, выбираемое для |
||
|
а |
|
ток |
|
|
сохранения низкой вероятности ложного детектирования, может быть длин- |
||
ным по сравнению с маркером кадра. Здесь стоит отметить, что сложность |
||
определения корреляции пропорциональна длине последовательности, по-
этому при использовании кодового слова коррелятор может быть относи- |
|||
тельно сложным. |
|
|
е |
|
т |
||
|
|
||
12.4. Заключ тельные замечания |
|||
|
о |
|
|
Точность тактовой синхронизации и синхронизации по фазе несущего |
|||
и |
|
|
|
колебания оказывает существенное влияние на вероятность ошибочного при- |
|||
ема информационныхл |
символов. Однако узкополосность процессов измене- |
||
ния фазыбнесущего колебания и времени запаздывания позволяет осуществлять эффект вную синхронизацию (реализующую характеристики помехо-
устойчивостиБи процесса демодуляции, близкие к потенциальным). Следует отметить, что ввиду сильной узкополосности (по сравнению с информационным трактом) устройств синхронизации для их входа в стационарный следящий режим требуется достаточно большой промежуток времени. Это особенно касается схем синхронизации управляемых решением. Для ускорения процесса входа в синхронный режим применяют специальные методы поиска (обучения) устройств синхронизации.
313
13.УПЛОТНЕНИЕ И МНОЖЕСТВЕННЫЙ ДОСТУП
13.1. Общие принципы осуществления множественного доступа к каналам связи
Создание любой системы электросвязи всегда подразумевает использование некоторого ресурса связи, и эффективность такой системы связи в первую очередь оценивается эффективностью использования ее ресурса.
Ресурсом связи называется совокупность физических характеристик
канала связи, доступных для передачи информации. |
Р |
|
|
В системе связи критерием эффективности использования ресурса свя- |
|
зи является достижение максимальной пропускной способности (общей скорости передачи данных) в реализованных ею каналах.
Существует лишь 3 способа увеличения пропускной способности. Пер-
вые 2 непосредственно следуют из уравнения Шеннона: |
И |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Eb |
|
|
|
|
|
|
У |
|||
C F log |
2 |
1 |
|
, бит/с, |
|
|
|
|
|||||
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
N0 |
|
|
|
|
|
|
|||
где F – ширина полосы частот канала; |
E |
|
Г |
|
|||||||||
b |
– отношение энергии, приходя- |
||||||||||||
|
|||||||||||||
|
|
|
|
|
|
|
|
|
N0 |
Б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
щейся на один бит передаваемой информ ции, к спектральной плотности |
|||||||||||||
шума. |
|
|
|
|
|
|
|
|
|
|
|
|
|
Таким образом, для увелич ния пропускнойа |
способности возможно: |
||||||||||||
– за счет увеличения F ; |
к |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
– за счет увеличения |
Eb |
. |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
N0 |
е |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Третий спос б увеличения C заключается в увеличении эффективно- |
|||||||||||||
|
|
|
|
|
т |
|
|
|
|
|
|
||
|
|
|
о |
|
|
|
|
|
|
|
|||
сти доступа к ресурсу связи. Последнее означает необходимость такого пла-
нирования распределен |
я ресурса связи между пользователями системы свя- |
|||
|
|
|
л |
|
зи, |
при котором, все ф |
зические свойства канала связи использовались бы |
||
|
|
|
б |
|
максимально эффективнои. |
||||
|
|
Распреде ение ресурса связи в свою очередь задается методом множе- |
||
|
информациРассмотрим наиболее общие вопросы распределения ресурса связи |
|||
ственного доступа, под которым понимается способ объединения сигналов |
||||
Б |
|
|
||
( |
|
|
онных потоков) различных пользователей для совместного ис- |
|
пользован я ресурса связи.
между многими пользователями.
Будем считать, что системе связи выделен или определен некоторый ресурс связи. Или, иными словами, определена некоторая область (пространство) в общей совокупности каналов, которую может занимать данная система связи как физический объект. Например, канальное пространство, выделенное системе связи, может быть ограничено диапазоном используемых частот, диапазоном во времени, когда разрешена передача, территорией, где
314
разрешена работа, разрешенными пространственными характеристиками (свойствами) используемых электромагнитных колебаний и пр.
Доступ к ресурсу связи для различных пользователей должен осуществляться на принципах исключения взаимного влияния передачи информации одних пользователей на передачу информации другими пользователями.
Исходя из этого наиболее общее условие осуществления множественного доступа (условие ортогональности выделяемого различным пользователям ресурса) может быть сформулировано следующим образом:
|
|
|
|
|
|
Р |
|
|
|||||||
|
... |
Ri ( )R j ( )d |
0 , |
И |
(13.1) |
||
i |
|
|
|
|
|
|
|
|
|
|
|
i j |
|
|
|
где R ( ) – функция, характеризующая ресурс, выделяемый i-му пользовате-
лю; – вектор параметров, характеризующий особенности имеющегося ре- |
|||||
сурса связи. |
|
|
|
У |
|
Определим основные параметры, характеризующие выделенный (ис- |
|||||
пользуемый) ресурс связи. |
|
|
Г |
||
|
|
|
|
||
1. |
Диапазон используемых ч стот. |
Интуитивно понятно, что если |
|||
|
|
|
|
Б |
|
выделенные пользователям ресурсы |
Ri ( ) |
х р ктеризуются непересекаю- |
|||
щимися диапазонами частот, то |
|
|
ние по частоте произведений ре- |
||
|
|
|
а |
|
|
сурсов выделяемых различным пользователям будет (в идеальном случае) |
|||||
|
|
к |
|
|
|
|
|
интегриров |
|
|
|
всегда приводить к нулевому знач нию. На данном свойстве ресурса связи |
|||||
основан метод множественного дос упа FDMA (Frequency Division Multiple Access) или множественный дос уп с частотным разделением. В этом случае
пользователю выделяются |
пределенные поддиапазоны закрепленной за си- |
||
стемой связи полосы част т. |
|||
|
|
|
т |
2. |
Время |
|
. Если различные пользователи осуществляют пе- |
|
|
о |
|
редачу на непересекающ хся интервалах времени, то в конкретный интервал |
|||
времени нену евое значение имеет ресурс только одного из абонентов и, |
|
|
передачи |
л |
|
б |
|
следовательно, о еспечивается выполнение общего условия множественного доступаи, поскольку ресурсы всех других абонентов в это момент времени равныБнулю. Данное свойство используется для осуществления множествен-
ного доступа по методу TDMA (Time Division Multiple Access) или множе-
ственного доступа с временным разделением. Каждому пользователю выделяются периодически временные интервалы, не пересекающиеся с временными интервалами, выделяемыми другим пользователям.
3. Форма несущего колебания. В наиболее общей трактовке отмеченные выше методы реализации множественного доступа тоже используют отличия в форме несущего колебания, поскольку использование различных поддиапазонов частот (при FDMA) означает использование различных несущих колебаний (например, cos( 1t ) и cos( 2t ) , именно отличия данных ко-
315
лебаний обеспечивают выполнение условия ортогональности выделяемого различным пользователями ресурса), аналогичная ситуация имеется и при реализации TDMA. В этом случае используются различные (не перекрывающиеся во времени) импульсные несущие колебания. На основании вышеизложенного необходимо уточнить, что когда идет речь об отличиях формы несущего колебания, как правило, подразумевают более «тонкие» отличия несущих колебаний и предполагается, что возможно выполнение условия ортогональности и при совпадении несущей частоты и времени передачи. Использование данной характеристики канала (ресурса связи) используется ме-
тодом множественного доступа CDMA (Code Division Multiple Access) или множественного доступа с кодовым разделением. Пользователю выделяются
определенные элементы набора ортогонально (либо почти ортогонально)
ватели находятся в конкретных точках пространства. СоответственноИ внесение определенных ограничений на направление излучения и приема сигналов
распределенных кодов (несущих сигналов), каждый из которых использует
весь диапазон частот и интервалов времени, выделенных для системы связи. |
|
4. |
Р |
Пространственные характеристики. Обычно конкретные пользо- |
|
конкретных пользователей может приводить к выполнениюГУусловий ортогональности выделяемых ресурсов. Подобные ограничения используются при реализации технологии SDMA (Space Division Multiple Access) или простран-
ственного множественного доступа. В этом случаеБс помощью антенной системы с несколькими узкими диаграмм ми излучения сигналы разделяются и
направляются в разные стороны, данный метод допускает многократное ис- |
||||
|
|
|
|
а |
пользование одного частотного диапазона и наибольшее распространение |
||||
нашел в спутниковых системах связик(своеобразный эквивалент технологии |
||||
SDMA это использование различных проводных или кабельных соединений |
||||
для различных пользова елей). |
е |
|
||
|
|
|||
5. |
Поляризаци нные характеристики электромагнитной волны. Из- |
|||
вестно, |
что поляризаци нные характеристики электромагнитной волны ока- |
|||
|
|
т |
|
|
|
о |
|
|
|
|
и |
|
|
|
зывают существенн е вл яние на преобразование энергии электромагнитного поля в энерг ю электрического тока, протекающего через проводники
условие ортогональности может быть реализовано использованием различнымииа онентами различных (ортогональных) поляризационных характерист к электромагнитной волны. На данном свойстве ресурса связи основан
различнойбконфигурации и пространственной ориентации. Соответственно
Бметод множественного доступа PDMA (Polarization Division Multiple Access)
или множественный доступ с поляризационным разделением. В данном случае разделение сигналов основывается на избирательности приемных антенн к положению вектора электрического поля (вертикальная, горизонтальная) или к направлению вращения данного вектора (вправо или влево). Данный метод наибольшее распространение нашел в радиорелейной и спутниковой связи.
При построении современных систем связи, как правило, используют несколько методов множественного доступа, в чистом виде используют крайне редко.
316

13.2. Множественный доступ с частотным разделением
(FDMA – Frequency Division Multiple Access)
Это один из самых распространенных методов множественного доступа, применяемых в системах радиосвязи. Принцип FDMA заключается в том, что весь частотный спектр разделяется между пользователями на равные или неравные частотные полосы (рис. 13.1). Причем каналы могут быть как симметричными в обоих направлениях, так и ассиметричными. Источники информации могут использовать выделенный им частотный ресурс неограниченно по времени, но при этом не должны создавать помехи соседним каналам. Чтобы избежать переходных помех, вводят специальный защитный ча-
стотный интервал между соседними каналами. Она не используется для пе- |
|
|
Р |
редачи информации и поэтому снижает общую пропускную способность |
|
имеющегося канала связи. |
И |
|
|
Математически выполнение условия ортогональности используемых |
|
различными пользователями ресурсов связи может быть записано следую- |
||||||||||
|
|
|
|
|
|
|
|
У |
|
|
щим образом: |
|
|
|
Г |
|
|
||||
|
|
|
|
|
|
|||||
|
|
|
|
Б |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Sk (t)S*m (t)e j kt e j mt dt |
|
|
|
|
0 , |
(13.2) |
||||
Re |
|
|
|
|
||||||
|
|
а |
|
|
k m |
|
|
|||
|
|
к |
|
|
|
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
пользуемые для сигнал в различныхт пользователей; * – операция комплексного сопряжения. Для беск нечного интервала интегрирования при различ-
где Sk (t) и Sm (t) – комплексные огибающие сигналов различных пользова-
телей (в общем случае совпадать); k и m – несущие частоты, ис-
ных несущих частотах всегда выполняется условие ортогональности, так как |
||||||||
|
|
|
|
могут |
|
|
|
|
|
|
|
и |
|
|
0 . |
|
|
|
|
л |
|
Re e j k t e j mt dt |
(13.3) |
|||
|
|
|
|
|
k m |
|
||
|
|
|
|
|
|
|||
На практике бесконечный интервал интегрирования означает выделе- |
||||||||
|
б |
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
|
ние пользователю полосы частот с шириной, равной 0 Гц (невозможна передача информации). Поэтому условие ортогональности должно выполняться при конечных интервалах интегрирования (обычно равных времени корреляции комплексной огибающей используемых сигналов). Данное требование накладывает ограничения на минимально необходимый разнос между несущими частотами k и m . Обычно k m , где – ширина
(двусторонняя) эффективной полосы частот комплексной огибающей используемого сигнала.
317

|
|
|
|
|
|
|
Р |
|
|
|
|
|
|
И |
|
|
|
|
|
|
У |
|
|
|
|
|
|
Г |
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
а |
|
|
|
|
|
|
|
к |
|
|
|
|
|
Рис. 13.1. Принцип орг низ ции FDMA |
|
|
||||
|
|
т |
|
|
|
|
|
13.3. Множественный доступ с временным разделением |
|||||||
(TDMA – Time Division MultipleеAccess) |
|
|
|
||||
Основной |
принцип |
TDMA заключается в том, что имеющийся ресурс |
|||||
разделяется между участникамио информационного обмена на циклически повторяющиеся промежутки времени (рис. 13.2). Промежутки времени полу-
менные ботрезкил. В такой ситуации главное, чтобы сигналы соседних таймслотов не накладывались друг на друга. Это может быть вызвано как слишком высокой мощностью передачи, так и помехами в канале, несовершенством
чили название «таймслот» (timeslot, TS). При этом абонент может использо-
вать всю ширину выделенной полосы частот, но только в определенные вре-
Биспользуемогои оборудования. Чтобы избежать подобных межслотовых помех, часто вводят специальный защитный временной интервал. Таким образом, если часть энергии одного передатчика просочится за пределы отведенного ему таймслота, то она будет оказывать воздействие лишь на защитный интервал, не несущий информацию. Введение такого интервала снижает общую пропускную способность канала связи, но необходимо для поддержания заданных характеристик качества обслуживания.
318

Рис. 13.2. Структура цикла TDMA
Математически выполнение условия ортогональности используемых
различными пользователями ресурсов связи может быть рассмотрено следу- |
||||
ющим образом: |
|
|
|
Р |
|
|
И |
||
|
|
|
||
|
|
|
||
|
|
0 ,У |
(13.4) |
|
Re Sk (t)S*m (t)e j 0t e j 0t dt |
||||
|
|
k mГ |
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
Б |
|
где Sk (t) gF ( t k )Sk (t) и Sm (t) gF ( t m )Sm (t) – комплексные огибаю- |
||||||||||||
щие сигналов различных пользователей; |
а |
|
||||||||||
|
|
|
1 |
|
t |
|
/ 2 |
|
|
|
||
|
|
|
|
|
|
|
|
|||||
g |
|
( t ) |
|
|
|
|
|
– формирующий TDMA импульс; – длительность ис- |
||||
|
|
|
|
|
|
|||||||
|
F |
|
|
|
t |
/ 2 |
|
к |
|
|
||
|
|
|
0 |
|
|
еi |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
пользуемых интервалов передачи; Sk (t) и Sm (t) – информационные состав- |
||||||||||||
ляющие комплексных гибающих различных пользователей (могут совпа-
дать). |
|
|
т |
|
|
|
|
|
|
|
|
|
|
Условие ортогональности выполняется, так как |
|
|
||||
|
|
о |
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
л gF ( t k )gF ( t m )dt 0 |
|
. |
(13.5) |
||
|
б |
|
|
k m |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
Приэтом ортогональность сохраняется и при сокращении интервала |
||||||
Б |
|
|
|
|
|
|
интегрирования до интервала корреляции информационной составляющей, равного .
319
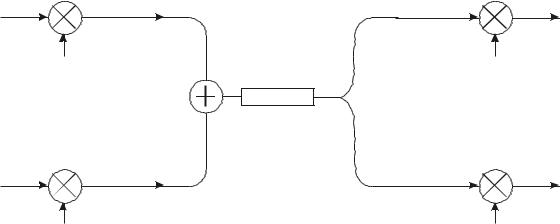
13.4. Метод множественного доступа с кодовым разделением
(CDMA – Code Division Multiple Access)
Этот метод отличается от двух других наиболее распространенных методов разделения каналов FDMA и TDMA тем, что коды в отличие от времени и частоты не являются явным ресурсом канала связи. Несмотря на сложность реализации, данный метод используется в радиосвязи уже довольно давно, т.к. обладает некоторыми преимуществами, которых не имеют другие методы множественного доступа.
Принцип CDMA заключае ся в том, что каждому источнику информации назначается индивидуальный код (канальный код или код канала), при
|
Кодированный |
|
|
|
|
Смесь |
|
|
|
Сигнал 1 |
сигнал 1 |
|
|
|
сигналов |
|
|
Сигнал 1 |
|
|
|
|
Среда |
|
|
|
|
Р |
|
|
|
распространения |
|
|
|
||||
Ортогональный |
|
сигнала |
|
|
|
|
|||
|
|
|
Ортогональный |
||||||
|
код 1 |
|
|
|
|
|
|
|
код 1 |
|
|
|
|
|
|
|
|
И |
|
|
Кодированный |
|
|
|
|
|
У |
|
|
|
|
|
|
|
Г |
|
|
||
Сигнал 2 |
сигнал 2 |
|
|
|
|
|
Сигнал 2 |
||
|
|
|
|
|
|
Смесь |
|
|
|
|
|
|
|
|
Б |
|
|
|
|
Ортогональный |
|
|
|
сигналов |
Ортогональный |
||||
|
|
а |
|
||||||
|
код 2 |
|
|
|
|
|
код 2 |
||
|
|
|
|
|
|
|
|
||
|
|
|
к |
|
|
|
|
|
|
|
Рис. 13.3. Принцип организации CDMA |
|
|||||||
|
|
е |
|
|
|
|
|
|
|
|
дирует |
|
|
|
|
|
|
|
|
помощи которого н к |
|
передаваемое сообщение. Приемник инфор- |
||
мации также знает этот |
, и его задача в том, чтобы выделить закодирован- |
|||
|
|
код |
|
|
ное сообщение нужного отправителя из всего потока других сообщений. В |
||||
|
и |
|
|
|
этом и зак ючается вся сложность, т. к. коды должны быть как можно мень- |
||||
|
л |
|
|
|
ше |
друг на друга, даже при временном смещении сообщений. На ма- |
|||
тематпохожическомбязыке свойство «похожести» называется корреляцией. Таким Бобразом, закодированные сообщения должны обладать как можно меньшей корреляц ей. Этим свойством обладают ортогональные коды, взаимное скалярное произведение которых равно 0. На практике удается получить не полностью ортогональные коды, а почти ортогональные. Если бы можно было сгенерировать бесконечное число полностью ортогональных кодов, то в одном канале связи смогут одновременно работать бесконечное число абонентов. Из-за неполной ортогональности кодов сигналы различных источников могут создавать помехи друг на друга. Причем чем выше мощности сигналов, тем ощутимее может оказаться влияние. Поэтому число одновременно
320
работающих абонентов и максимально возможная передаваемая мощность в системе с CDMA ограничены.
Условие ортогональности при использовании технологии CDMA определяется следующим образом:
|
|
|
0 , |
|
Re Sk (t)S*m (t)e j 0te j 0t dt |
|
(13.6) |
||
|
|
k m |
|
|
|
|
|
|
|
|
|
(t) g |
|
(t)Si |
|
|
(t) g |
|
(t)Si |
Р |
где S |
k |
cdma k |
(t) и S |
m |
cdma m |
(t) – комплексные огибающие |
||||
|
|
k |
|
|
k |
И |
||||
сигналов различных пользователей; gcdma k (t) |
– составляющая комплексной |
|||||||||
огибающей, представляющая канальный код, определенный k-му пользовате- |
||||||||
|
|
|
|
|
|
|
У |
|
лю. Соответственно для обеспечения ортогональности канальные коды |
||||||||
должны удовлетворять следующему условию: |
|
|
Г |
|
||||
|
|
|
|
|
|
|
||
|
|
|
|
|
|
Б |
|
|
Re |
gcdma k (t)g*cdma m (t)dt |
|
0 . |
(13.7) |
||||
|
|
|
|
|
k m |
|
|
|
|
|
|
а |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
к |
|
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
13.5. Метод доступа с пространственным разнесением |
|
|||||||
пользователей (SDMA – Space Division Multiple Access) |
|
|||||||
SDMA является ме одом дос упа к каналам связи, основанным на про-
редающих и пр емныхобластейантенн в данных областях возможно одновременное
странственном разнесении пользова елей услуг связи. В этом случае путем
использования направленных ан енных систем организовываются несколько |
|
пространственных |
т. За счет пространственной избирательности пе- |
использование «одинаковых» сигналов (сигналов, совпадающих по времени действия, занимаемой полосе частот, используемому канальному коду). Та-
л ким образомболее, возможно повышение эффективности использования ресурса
теннБи(«умных» антенн), которая позволяет с высокой точностью определять пространственное местоположение абонентов и концентрировать излучение и прием в их направлении.
связи. Метод организации пространственного множественного доступа станов тся на привлекательным при использовании технологии Smart ан-
321
13.6. Метод доступа, основанный на использовании поляризационных свойств электромагнитного излучения
(PDMA – Polarization Division Multiple Access)
В результате согласованного использования поляризаций передающей и приемной антенны возможен раздельный прием электромагнитных излучений с ортогональными поляризациями (например, горизонтальной и вертикальной или с правой и левой круговыми поляризациями), что практически позволяет вдвое повысить эффективность использования выделенного ресурса связи. Данный метод множественного доступа получил широкое распространение в космических и радиорелейных линиях связи прямой видимости, поскольку при распространении радиоволн вне условий прямой видимости (за счет переотражений, дифракции, рефракции и пр.) наблюдается явление
деполяризации электромагнитной волны. |
|
|
Р |
|
|
|
|
|
|
И |
|
13.7. Мультиплексирование с ортогональным частотным |
|||
разделением (OFDM – Orthogonal Frequency Division Multiplexing) |
|||
|
У |
|
|
|
Г |
|
|
OFDM – мультиплексирование с ортогональным частотным разделени- |
|||
ем использует большое количество близкоарБсположенных ортогональных
поднесущих колебаний. Каждое поднесущее колебание модулируется по
обычной схеме линейной модуляции (н пример BPSK или QAM) c достаточ- |
|||||||||
|
|
|
|
|
|
е |
|
|
|
но низкой скоростью, Большая с орость передачи сохраняется благодаря |
|||||||||
большому количеству использу мыхкподнесущих колебаний (обычно не- |
|||||||||
сколько сотен). |
|
|
т |
|
|
||||
|
|
|
|
|
|
|
|||
По своей сути OFDM являе ся частным случаем FDMA. Принципиаль- |
|||||||||
|
|
|
|
о |
|
|
|
|
|
ной особенностью здесь являе ся синхронность используемых поднесущих |
|||||||||
частот. |
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для того чт бы п нять суть метода OFDM, рассмотрим следующий |
|||||||||
пример. |
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Пусть имеется многоканальный модулятор, формирующий на своих |
|||||||||
выходах N |
сигна ов с /2-BPSK. При этом каждый сигнал имеет несущее |
||||||||
и |
|
|
|
|
|
|
|
|
|
колебание видал |
|
|
|
|
|
|
|||
Б |
|
|
|
sн i( t ) A0 cos i 0t , |
i 1,2,...,N . |
(13.8) |
|||
|
|
|
|
||||||
Тогда сумма из N сигналов с /2-BPSK запишется следующим обра- |
|||||||||
зом: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N |
|
|
|
|
|
|
s ( t ) A0 |
Ci cos( i 0t ) , |
(13.9) |
|||
|
|
|
|
|
|
i 1 |
|
|
|
322

где Ci 1, модулирующие символы i -го модулятора. Обратим внимание на то, что выражение, стоящее в скобках, представляет собой разложение в ряд Фурье по гармоническим функциям совокупного сигнала s ( t ) . Аналогично
можно записать представление совокупного сигнала в виде комплексного ряда Фурье. При этом модулирующие символы могут рассматриваться как изменяющиеся амплитуды спектральных компонент совокупного сигнала.
На основании вышеизложенного может быть предложена следующая схема (рис. 13.4) формирования совокупного (многоканального) сигнала s ( t ).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Генератор |
|
Р |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
||||
|
|
С1 |
|
|
|
Фурье |
|
|
|
|
|
|
|
несущего |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
У |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
С2 |
|
|
|
|
|
|
|
|
|
|
|
колебания |
|
||||
|
|
С3 |
|
|
|
преобразованиедискретное |
|
|
|
|
|
|
Г |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A0cos( 0t) |
||||||
символыМодулирующие |
|
|
|
|
|
Комплексная |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
огибающая |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
совокупного |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
сигнала |
|
БКвадратурный |
s (t) |
||||||||
|
|
|
|
|
|
|
|
|
к |
|
|
||||||||
|
|
|
|
|
|
|
|
е |
|
|
|
|
модулятор |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
СN |
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
Обратне |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
л |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Б |
Р с. 13.4. Формирование многоканального сигнала OFDM |
|
|
||||||||||||||||
Модул рующие символы могут соответствовать любой линейной схеме дискретной модуляции, например, Ci 1 обеспечивает модуляцию под-
несущих по методу /2-BPSK; |
Ci 1 j1 – |
QPSK или |
OQPSK; |
Ci A jB – QAM и т.д. |
|
|
|
Необходимо отметить, что несимметричность |
исходного |
«спектра» |
|
C1,....,CN приводит к комплексному характеру получаемой в результате об-
ратного преобразования Фурье временной реализации совокупного модулированного сигнала.
323

Основным преимуществом OFDM по сравнению со схемами, использующими одно несущее колебание, является еѐ способность противостоять сложным условиям в канале. Например, бороться с узкополосными помехами и частотно-избирательным затуханием, вызванным многолучевым характером распространения, без использования сложных фильтров-эквалайзеров. Кроме того, OFDM обеспечивает большую гибкость и адаптивность в распределении ресурса радиоканала между различными пользователями (осуществляется простое перераспределение потоков данных между соответствующими входами обратного преобразования Фурье).
Выделение информации из совокупного сигнала OFDM осуществляется с использованием операции прямого преобразования Фурье.
Спектр сигнала с OFDM приведен на рис.13.5.
|
S(f) |
|
|
|
|
|
|
|
|
|
|
Р |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
|
|
|
|
|
|
|
|
|
|
|
У |
|
|
|
|
|
|
|
|
|
|
|
Г |
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
|
|
|
|
|
к |
|
|
|
|
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
|
|
|
т |
|
|
|
|
|
f |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
Р с. 13.5. Спектр сигнала с OFDM |
|
|
||||||
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
л |
|
|
|
|
|
|
|
|
|
|
|
б |
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
|
|
|
|
|
324
ЗАКЛЮЧЕНИЕ
Актуальность и важность вопросов разработки и эксплуатации систем цифровой радиосвязи определяется их высокой востребованностью в различных отраслях экономики. Эта ситуация вызвана прежде всего требованиями высокого качества предоставляемых услуг, недостижимого в принципе в аналоговых системах, при формировании, передаче, приеме и обработке информации.
Теоретические основы цифровой радиосвязи излагаются в ряде литера-
турных источников. Как правило, это переводные издания, многие из кото-
лагаются с использованием достаточно сложного математическогоИРаппарата, что затрудняет их эффективное использование для инженерной подготовки.
рых написаны научно-популярным языком и не в полной мере отражают све-
дения, необходимые инженеру-разработчику цифровых систем. Существует
также и вторая крайность – в отдельных изданиях теоретические основы из-
В данном пособии авторы постарались в какой-то мере ликвидировать пробелы существующих изданий как с точки зрения глубины и полноты из-
пособия изложены достаточно полно (например, глава 11), некоторые главы
лагаемого материала, так и с точки зрения его доступности. Отдельные главы |
|
|
У |
Г |
|
Б |
|
представлены фрагментарно. В пособии есть абсолютно новый материал, ранее излагавшийся лишь в научных публик циях, например глава 8.
При написании материала авторы использовали собственный опыт и
знания, а также свои разработки по созд нию различных систем прие- |
||||||||
|
|
|
|
|
|
|
|
а |
ма/передачи информации, обесп ч нию их надежного и эффективного функ- |
||||||||
ционирования. |
|
|
|
|
к |
|||
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
т |
|
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
л |
|
|
|
|
|
|
|
б |
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
|
325
ЛИТЕРАТУРА
1.Прокис, Дж. Цифровая связь: пер. с англ.; под ред. Д. Д. Кловского / Дж. Прокис. – М. : Радио и связь. 2000. – 800 с.
2.Таненбаум, Э. Компьютерные сети. – 4-е изд. / Э. Таненбаум. – СПб. : Питер, 2010. – 992 с.
3.Скляр, Б. Цифровая связь. Теоретические основы и практическое применение. – 2-е изд., испр.; пер. с англ. / Б. Скляр. – М.: Издательский дом «Вильямс», 2003. – 1104 с.
4.Волков, Л. Н. Системы цифровой радиосвязи: базовые методыРи ха-пособие /5. Системы и сети цифровой радиосвязи : Иучеб.
|
|
|
|
|
|
|
|
У |
Н. И. Листопад [и др.]. – Минск: Изд-во Гревцова, 2009. – 200 с. |
||||||||
|
|
|
|
|
|
|
Г |
|
6. |
Гоноровский, И. С. Радиотехнические цепи и сигналы: учебник |
|||||||
|
|
|
|
|
|
Б |
|
|
для вузов / И. С. Гоноровский. – 3-е изд., перераб. и доп. – М.: Сов. радио, |
||||||||
1977. – 608 с. |
|
|
|
|
|
|
|
|
7. Хелд, Г. Технологии передачи |
данных |
. – 7-е изд. / Г. Хелд. – СПб. : |
||||||
|
|
|
|
|
|
|
||
Питер, К.: Издательская группа BHV, 2003. – 720 с. |
|
|||||||
|
|
|
|
к |
|
|
|
|
8. Шиман, Д. В. Метод псевдонер вномерного перемежения символов |
||||||||
|
|
|
е |
|
|
|
|
|
турбокода / Д. В. Шиман // Труды БГТУ. Сер. VI. Физ.-мат. науки и ин- |
||||||||
форм. – 2005. – Вып. XII. – С. 16–21. |
|
|
|
|
||||
9. |
Овчинников, А. М. TETRA – стандарт |
открытый для всех / |
||||||
А. М. Овчинников // Специальная |
ехника. – 1999. – № 4. – С. 21–29. |
|||||||
|
|
о |
|
|
|
|
|
|
10. Goldsmith, A. Wireless |
Communications / |
A. Goldsmith. – Cam- |
||||||
|
|
и |
|
|
|
|
|
|
bridge University Press, 2005.т–571 p. |
|
|
|
|
||||
11. |
Рыжков, А. В. Синтезаторы частоты в |
технике радиосвязи / |
||||||
А. В. Рыжков, В. Н. Попов. – М. : Радио и связь, 1991. – 264 с. |
||||||||
б |
|
|
|
|
|
|
|
|
12. |
Те екоммуникационные системы и сети: учеб. пособие. В 3 т. Т. 1: |
|||||||
и |
|
|
|
|
|
|
|
|
Современныелтехнологии / Б. И. Крук, В. Н. Попантонопуло, В. П. Шувалов;
под ред. проф. В. П. Шувалова. – 3-е изд., испр. и доп. – М. : Горячая линия- БТелеком, 2003. – 647 с.
13. Радиопередающие устройства: учебник для вузов/ В. В. Шахгильдян [и др.]; под ред. В. В. Шахгильдяна. – 3-е изд., перераб. и доп. – М. : Радио и связь, 2003. – 560 с.
14.Проектирование радиопередатчиков / В. В. Шахгильдян [и др.];
под ред. В. В. Шахгильдяна. – М. : Радио и связь, 2000. – 656 с.
326
15. Столингс, В. Компьютерные системы передачи данных / В. Столингс. – 6-е изд.; пер. с англ. – М.: Издательский дом «Вильямс», 2002. – 928 с.
16.Кульгин, М. Технологии корпоративных сетей. Энциклопедия / М. Кульгин. – СПб.: Питер, 1989. – 704с.
17.Олифер, В. Г. Компьютерные сети. Принципы, технологии, протоколы. / В. Г. Олифер. – СПб.: Питер, 2000. – 672 с.
18. Олифер, В. Г. Новые технологии и оборудование IP-сетей /
19.Листопад, Н. И. Моделирование и оптимизация глобальныхРсетей / Н. И. Листопад. – Минск : БГУ, 2000. – 156 с. И
20.Устав Международного Союза Электросвязи (МСЭ). – Женева,
1992. У
21.Об электросвязи: Закон Республики Беларусь от 19 июля 2005 г.
№45-3: одобр. Советом Респ. 30 июня 2005 г. – МинскГ, 2006. – 31 с.
22.Козел, В. М. Некоторые особенностиБтрафика и эффективности использования частотного ресурса в сетях подвижной связи Министерства внутренних дел / В. М. Козел, К. А. Ковалева, К. Л. Горбачев // Техника СВЧ и телекоммуникационные технологии: м тери лы 17-й Междунар. Крымской конф., Севастополь, 10–14 сент. 2007кг. – Т. 1.– С. 309–310.
23.Recommendation ITU еG.702 Digital Hierarchy bit rate.
24.Recommendation CCITT G.707 Synchronous digital hierarchy bit rate.В. Г. Олифер, Н. А. Олифер. – СПб.: БХВ – Санкт-Петербург, 2000. – 512 с.
25.Лайонс, Р.КорнЦифровая обработка сигналов / Р. Лайонс. – 2-е изд.; пер. с англ.– М. : ООО «Бин м-Пресс», 2006. – 656 с.
26.Корн, Г. Справ чник по математике: для научных работников и инженеров / Г. Корн, Т. . – М. : Наука, 1974. – 832 с.ти
|
|
л |
27. |
Мидд тон, Д. Введение в статистическую теорию связи / |
|
Д. Миддлтон; пер. с англ.; под ред. Б. Р. Левина. – М. : Сов. радио, 1962. |
||
и |
|
|
28. |
Т хонов, В. И. Статистическая радиотехника / В. И. Тихонов. – |
|
Б |
брад о, 1966. – 677 с. |
|
М. : Сов. |
||
29. |
Амиантов, И. Н. Избранные вопросы статистической теории свя- |
|
зи / И. Н. Амиантов. – М. : Сов. радио, 1971. – 416 с. |
||
30. |
Горяинов, В. Т. Статистическая радиотехника. Примеры и задачи: |
|
учеб. пособие для вузов / В. Т. Горяинов; под ред. В. И. Тихонова. – 2-е изд., перераб. и доп. – М. : Сов. радио, 1980. – 544 с.
31. Витерби, Э. Д. Принципы когерентной связи / Э. Д. Витерби; пер. с англ.; под ред. Б. Р. Левина. – М. : Сов. радио, 1970. –392 с.
327
32.Xiong, F. Digital modulation techniques /F. Xiong; Artech House, Inc. – Boston-London, 2000. – 669 p.
33.Венцель, Е. С. Теория вероятности / Е. С. Венцель. – Изд. 4-е, стереотип. – М. : Наука, 1969. – 576 с.
34. Шеннон, К. Работы по теории информации и кибернетике / К. Шеннон; пер. с англ. под ред. Р. Л. Добрушина и О. Б. Лупанова с предисловием А. Н. Колмогорова. – М. : Издательство иностранной литературы,
1963. – 827 с. |
|
|
|
|
|
|
|
|
|
|
|
||
35. |
Mengali, |
U. Synchronization techniques for |
digital receivers / |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Р |
U. Mengali, A. N. D’Andrea. – New-York, London: Plenum Press, 1997: –529 p. |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
И |
|
36. |
Витерби, |
А. Д. Принципы цифровой связи |
и |
кодирования / |
|||||||||
А. Д. Витерби; пер. с англ.; под ред. К. Ш. Зигангирова. – М. : |
адио и связь, |
||||||||||||
1982. –536 с. |
|
|
|
|
|
|
|
|
У |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||
37. |
Акулиничев, Ю. П. Теория электрической связи: учеб. пособие. / |
||||||||||||
Ю. П. Акулиничев. – СПб. : Лань, 2010. – 240 с. |
Г |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
|
|
|
|
|
|
к |
|
|
|
|
|
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
л |
|
|
|
|
|
|
|
|
|
|
|
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
|
|
|
|
|
|
328
Св. план 2011, поз. 78
|
|
|
|
|
Учебное издание |
|
|
|
|
|
||
|
|
|
|
Листопад Николай Измайлович |
|
|
|
|||||
|
|
|
|
Козел Виктор Михайлович |
|
|
|
|||||
|
|
|
Дубровский Василий Викторович и др. |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
Р |
|
|
|
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ |
И |
||||||||
|
|
|
ЦИФРОВОЙ РАДИОСВЯЗИ |
|||||||||
|
|
|
|
|
|
|
|
|
|
У |
|
|
|
|
|
|
УЧЕБНОЕ ПОСО ИЕ |
Г |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
|
|
|
|
|
к |
|
|
|
|
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
Редактор Г. С. Корбут |
|
|
|
|
||||
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
Корректор Е. Н. Батурчик |
|
|
|
|||||
|
|
|
Компьютерная верстка Ю. Ч. Клочкевич |
|
|
|||||||
|
|
л |
|
|
|
|
|
|
|
|
|
|
|
б |
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
|
|
|
|
|
Подписано в печать 11.12.2012. Формат 60х84 1/16. Бумага офсетная. Гарнитура «Таймс».
Отпечатано на ризографе. Усл. печ. л Уч.-изд. л. 20,0. Тираж экз. Заказ 693.
Издатель и полиграфическое исполнение: учреждение образования «Белорусский государственный университет информатики и радиоэлектроники» ЛИ №02330/0494371 от 16.03.2009. ЛП №02330/0494175 от 03.04.2009. 220013, Минск, П. Бровки, 6
329
