Р

И

У

Г

Б

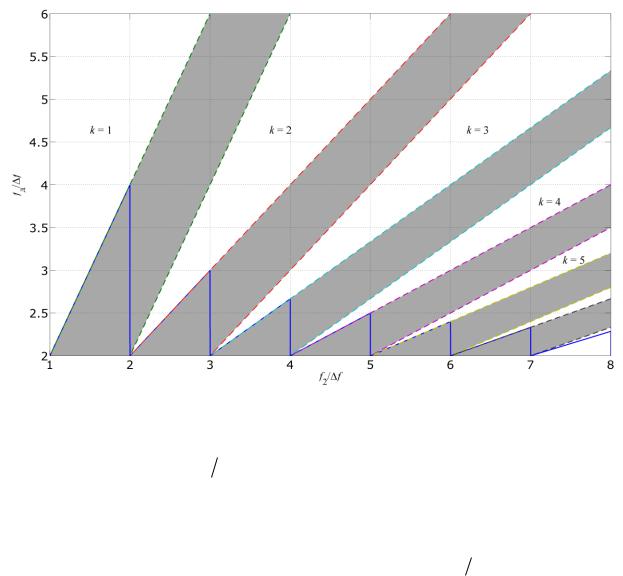
Рис. 4.3. Область допустимых значений частоты дискретизации

полосового сигнала (незатонированные участки)

а

к

Если отношение f2 f является целым числом, то минимально воз-

можная частота дискретизации полосового сигнала равна удвоенной полосе

занимаемых частот,

т. е.

fд 2 f

. В этом случае фрагменты спектров S ( f )

т

и S ( f ) будут соприкасаться друг с другом и результирующий спектр будет

сплошным на всѐм интервале часеот. Если отношение f2 f не является це-

о

лым, то частота дискре изации fд может быть равна значению, взятому из

и

некоторого интервала с гласно рис. 4.3. Для большинства практических при-

л

f

ложений значен е

д

задаѐтся равным среднему арифметическому крайних

допустимых значен й. В результате формируется спектр дискретного сигна-

б

ла с равными защитными интервалами между чередующимися участками

и

S ( f )

S ( f ) .

Б

писывается следующим образом:

sдn (t) s(t)xp (t)

,

(4.15)

X p ( ) Ck ( k д ) ,

(4.16)

k

Р

где д 2 T , а

И

и

sin k

и

2

jk д и

У

C

д

exp

.

k

T

k д и 2

2

Г

Спектр дискретного сигнала

Б

S

дn

( ) S( ) X

p

( )

C S( k ) .

(4.17)

k

д

kа

Из этого следует, что сп ктр дис ретного сигнала представляет собой

чередующиеся через д

к

исходного сигнала, умноженные на кон-

е

спектры

станту Ck . Следовательно, аналоговый сигнал может быть без искажений

го

восстановлен из дискре н

пу ѐм пропускания последнего через идеаль-

и

ный фильтр нижних част т.

б

случая опреде яется с едующим выражением:

и

лsдf (t)

и

s(kT )xp (t kT ) .

(4.18)

равно значению сигнала s(t) в момент взятия выборки. Используя выраже-

Б

s

(t)

, можно записать:

ние для идеального дискретного сигнала

д

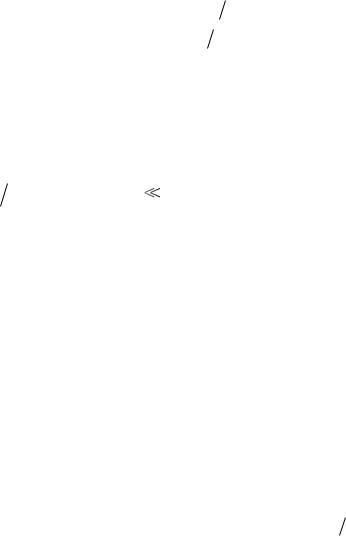
S

( ) X

( )S

( )

1

X

( )S( k ) ,

(4.20)

T k

дf

p

д

p

д

где

sin и

2

j

P( ) и

exp

и

.

(4.21)

и

2

2

ных. Указанный эффект называется эффектом

апертурной погрешности.

Р

Апертурная погрешность при плосковершинной дискретизации сигнала мо-

жет быть

скорректирована эквалайзером

с

передаточной функцией

Keq ( ) 1

X p ( ) . Если и

И

T , то в пределах диапазона частот основного

У

спектра S( ) апертурные искажения незначительны и ими можно прене-

бречь.

Г

Б

4.1.6. Теорема отсчѐтов в частотной области

В силу частотно-временной дуальности преобразований Фурье теорему

| t | T .

спектр

отчѐтов можно сформулировать и для

льной плотности сигнала, введя

понятие сигнала, ограниченного во времени. Сигнал s(t) называется ограни-

ченным во времени, если s(t) 0 всюдуза, исключением интервала времени

Спектр S( ) ограниченного во времени сигнала может быть точно

е

S(k д ) , взятых через равные ин-

представлен множеством своих значений

тервалы частоты, не превышающие значения д T :

т

sin T ( k )

о

д

.

(4.22)

S( )

S(k д )

T ( k д )

и

k

Иначе говоря, спектр, отображающий в частотной области сигнал ко-

нечной длительностил, точно описывается множеством дискретных значений

спектральной плотности, взятых через определѐнные равноотстоящие друг от

б

друга нтервалы частоты.

и

4.1.7. Выводы и практические рекомендации

Б