Добавил:

feelcame linker.pp.ua Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Харьковский национальный университет радиоэлектроники

Предмет:

Сотовые сети

Файл:

Листопад - Теоретические основы цифровой радиосвязи, (2012).pdf

Скачиваний:

Добавлен:

15.12.2018

Размер:

10.45 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 103 4 5 6 7 8 9 10 > Следующая >>>

Если объем алфавита источника равен k , а число связанных символов, которые необходимо учитывать при определении вероятности очередного символа, равно порядку источника n , то каждому символу может предше-

ствовать M k n различных сочетаний символов (состояний источника), влияющих на вероятность появления очередного символа xi . А вероятность появления в сообщении любого из k возможных символов определяется условной вероятностью P( xi / xi 1 ,xi 2 ,...,xi n ) с учѐтом предшествующих симво-

лов xi 1 ,xi 2 ,...,xi n ,

т. е. с учѐтом M возможных состояний. Эти состояния

обозначим как q1 , q2 , ...,qM .

Энтропия такого дискретного источника определяется в два этапа.

1. Вычисляются условные энтропии источника в каждом из M состоя-

ний, считаем эти состояния известными:

для состояния q1:

H( x / q1 ) P( xi / q1 )log2 ( P( xi / q1 ) );

i 1

для состояния q2 : H( x / q2 ) P( xi / q2 )log2 ( P( xi

/ q2 ) ) ;

(3.4)

i 1

)log Г( P( x / q

для состояния q

H( x / q

) P( x / q

) ).

i 1

2. Далее находим энтропию

H (x) путѐм усреднения по

всем состояниям q :

источника

(3.5)

H( x ) P( q j

)H( x / q j ) .

j 1

Окончательно получаем

/ q j )log2 ( P( xi

/ q j

) ) .

(3.6)

H( x )

P( q j ) P( xi

j 1

i 1

наличии

корреляционных связей между символами в эргодиче-

ском сточнике энтропия уменьшается,

так как при этом уменьшается не-

При

определѐнность выбора символов и в ряде случаев часть символов можно угадать по предыдущим или ближайшим символам.

3.4. Избыточность источника

Как было показано выше, энтропия максимальна при равновероятном появлении элементов сообщения и отсутствии между ними корреляционных связей. При неравномерном распределении вероятности появления символов

и при наличии корреляционных связей между символами энтропия уменьшается.

Чем ближе энтропия источника информации к максимальной, тем рациональнее работает источник. Чтобы судить о том, насколько хорошо использует источник свой алфавит, вводят понятие избыточности источника сообщений

g	Hmax ( x ) H( x )	log2	( k ) H( x )	.	(3.7)
	Hmax ( x )	log2( k )

редавая). Р Однако преднамеренная избыточность в сообщениях иногда использу-

Наличие избыточности приводит к загрузке канала связи передачей лишних символов, которые не несут информации (их можно угадать и не пе-

ется для повышения достоверности передачи информации –Инапример, при помехоустойчивом кодировании в системах передачи информации с исправ-

лением ошибок. Большую избыточность имеет любая устнаяУречь. Например, избыточность русского языка (как и других) – около 50 %. Благодаря избы-

точности облегчается понимание речи при наличии дефектов в произноше-
									Г
нии или при искажениях речевых сигналов в каналах связи.
									Б
3.5. Производительность источни
							а
Производительность						к
Производительность							определяется количеством информа-
ции, передаваемой в единицу							. Измеряется производительность ко-
				времени
личеством двоичных единиц информации (бит) в секунду. Если все элементы
сообщения имеют одинак вую дли ельность , то производительность ис-
точника равна			источника
			источника
		о
	и			R		H( x )		.		(3.8)
				R				.		(3.8)

л
л
Если
же различные элементы сообщения имеют разную длительность,
Б										, рав-
то в пр ведѐннойб	формуле надо учитывать среднюю длительность									, рав-
ную математическому ожиданию символа:
						k
					i P( i ) .					(3.9)
						i 1

Однако в последней формуле P( i ) можно заменить на P( xi ) (веро-

ятность i-го элемента сообщения), так как эти вероятности равны. В результате получаем

i P( xi ) ,

(3.10)

i 1

а производительность источника будет равна

H( x )

(3.11)

Mаксимально возможная производительность дискретного источника

равна Rmax

Hmax ( x )

Для двоичного источника, имеющего одинаковую длительность эле-

ментов сообщения, имеем

Rmax

бит/с.

При укрупнении алфавита в слова по n символов, имеем

nlog2 ( 2 )

Rmax

бит/с.

Таким образом,

путѐм ув лич ния размерности алфавита увеличить

производительность источника н льзя, так как в этом случае и энтропия, и длительность сообщения одновременно возрастают в одинаковое число раз.

Увеличить производи ельнос ь можно путѐм уменьшения длительности элементов сообщения, днако возможность эта ограничивается полосой пропускания канала связи. Поэтому производительность источника можно

увеличить за счет					экономного использования полосы пропускания,
				более
например, путем пр менения сложных многоуровневых сигналов.
			и
		л
3.6. Совместная энтропия двух источников
	б
Пусть меется два дискретных источника с энтропиями H( x ) и H( y )
и
Б

и объѐмами алфавитов k и m .

Объединим оба эти источника в один суммарный источник и определим совместную энтропию. Элементарное сообщение на выходе системы содержит элементарное сообщение xi и сообщение y j . Алфавит сложной си-

стемы будет иметь объѐм k m , а энтропия будет равна

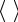
	k m
	H( x, y ) P( xi , y j )log P( xi , y j ) .										(3.12)
	i 1 j 1
По теореме умножения вероятностей
	P( x, y ) P( x )P( y / x ) P( y )P( x / y )										(3.13)
с учетом этого имеем
	k m
	H (x, y) P(xi , y j ) log P(xi , y j ) H (x) H ( y / x)										(3.14)
	i 1 j 1										(3.14)
		H ( y) H (x / y).							Р
									Р
Здесь	H( y / x ) P( xi , y j	)log2 ( P( y j				/ xi	) ) – условная			энтропия
	i j							И
								И
источника y	относительно источника x . Она показывает, какую энтропию
имеют сообщения y , когда уже известно сообщение							x .	У
Если источники независимы,		то P( y / x ) P(Гy ) и H( y / x ) H( y ). В
этом случае	H( x, y ) H( x ) H( y ) .			Б
				Б
Если источники частично зависимы, то H( x, y ) H( x ) H( y ).
Если источники полностью зависимы ( x						и y cодержат одну и ту же
			а
информацию), то H( y / x ) 0 и H( x, y ) H( x )					H( y ).
		к
	е
3.7. Скорость передачи и пропускная способность канала связи
В дискретной с стеметсвязи при отсутствии помех информация на вы-

ходе канала связи полностью совпадает с информацией на его входе, поэтому
				о
			и
		л
скорость передачи нформации численно равна производительности источ-
ника сообщений:
	б				C R( x )	H( x )	.	(3.15)
					C R( x )		.	(3.15)

и
и
При наличии помех часть информации источника теряется и скорость
Б

передачи информации оказывается меньшей, чем производительность источника. Одновременно в сообщение на выходе канала добавляется информация о помехах (рис. 3.2). Поэтому при наличии помех необходимо учитывать на выходе канала не всю информацию, сообщаемую источником, а только взаимную информацию.

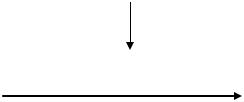
В процессе передачи символы входного алфавита претерпевают искажения и преобразуются в символы выходного алфавита канала связи, которые в общем случае могут не совпадать со входными.

Под взаимной информацией будем понимать приращение знания о входных символах при приеме (получении) выходных символов. Данное приращение характеризуется приращением апостериорной вероятности (ве-

роятности после наблюдения конкретного выходного символа y j ) конкрет-

ного символа входного алфавита xi относительно априорной вероятности

(вероятности, которая была до приема символа выходного алфавита) данного

символа.

Передающая

Приемная

сторона

Помеха

Входной

Выходной

алфавит

x1, x2 , ..., xk

y1, y2 , ..., ym

Канал связи

Р с. 3.2.тПроцесс передачи информации

В двоичных ед н цах информации данная взаимная информация за-

пишется с едующим образом:

P(xi

/ y j )

P(xi /

y j )P( y j )

log

y j xi

P(xi )

P(xi )P( y j )

(3.16)

log2

P(xi , y j )

I (xi

) I ( y j

) I (xi , y j ),

P(x )P( y

)

I( xi ) log2( P( xi )),

(3.17)

I( y j ) log2( P( y j )),

(3.18)

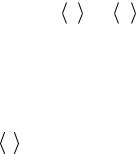
I( xi , y j ) log2( P( xi , y j )),			(3.19)
Взаимная информация обладает свойством симметрии I y	j	x	I x y	j
	j	i	i	j

и характеризует количество информации, которое приносит конкретный символ выходного алфавита y j (принятый символ) относительно конкретно-

го символа входного алфавита xi (переданного символа) и наоборот.

Для того чтобы охарактеризовать процесс передачи информации в целом, осуществим усреднение взаимной информации с учетом вероятностей появления входных и выходных символов.

Пропускной способностью канала связи (канала передачи информации) C называется максимально возможная скорость передачи информации по ка-

H y x H x y P(xi , y j )I y x P(xi , y j )Ix y

i j

P(xi , y j

P(xi , y j )

) log2

H (x) H ( y)

H (x, y)

(3.20)

P(x )P( y

)

H (x) H (x / y) H ( y) H ( y / x).

Таким образом, информационная производительность канала связи с

шумами определяется следующим образом:

H y x

R(x, y)

H (x) H (x / y) R(x) R(x / y)

тR( y) R( y / x),

(3.21)

где R( x )

( x ) g

–

производительность источника;

R( x / y ) –

maxи

«ненадѐжность» канала, (потери) в единицу времени; R( y) – энтропия вы-

ходного сообщения в единицу времени;

R( y / x) R(n) – энтропия помех

(шума) в ед н цу времени; g – избыточность источника.

налу
C max R( x, y ) .	(3.22)

Таким образом, пропускная способность канала связи равна максимальной производительности источника на входе канала, полностью согла-

сованного с характеристиками этого канала, за вычетом потерь информации в канале из-за помех.

Для бинарного канала с шумами пропускная способность равна

C max R( x, y ) max R( y ) R( y / x ) .

(3.23)

В случае бинарного канала связи размерность выходного алфавита равна 2, следовательно, максимальная производительность канала связи на выходе равна

max R( y )

log

(3.24)

и, следовательно, пропускная способность канала запишется следующим об-

разом:

(3.25)

max 1 H( y / x ) .

Определим условную энтропию

H( y / x )

P( x

, y

i 1 j 1

P( x1 )P( y1

/ x1 )) P( x1 )P( y2 / x1 )log2 ( P( y2 / x1 ))

/ x1 )log

2 ( P( y1

P( x2

)P( y1

/ x2

)log2

( P( y1 / x2 )) P( x2 )P( y2 / x2 )log2 ( P( y2 / x2 ))

) P( x

) P

log

( P

)

P( x

) 1иP log

) Pe log2 ( Pe ) P( x2 ) 1 Pe log2 (1 Pe )

P( x2

log2( Pe ) 1 Pe log2(1 Pe ),

(3.26)

где Pe – вероятность ошибочного приема.

Таким образом, пропускная способность бинарного канала с шумами

равна

1 H

1 P log

( P

) (1 P )log

(1 P )

(3.27)

где He – энтропия ошибок при приеме.

В канале без помех пропускная способность равна производительности источника.

Для эффективного использования пропускной способности канала необходимо его согласование с источником информации на входе. Такое согласование возможно как для каналов связи без помех, так и для каналов с помехами на основании двух теорем, доказанных К. Шенноном.

1-я теорема (для канала связи без помех):

Если источник сообщений имеет энтропию H (бит на символ), а канал

сообщения таким образом, чтобы передавать информацию по Рканалу со средней скоростью, сколь угодно близкой к величине C , но не превзойти еѐ.

связи – пропускную способность C (бит в секунду), то можно закодировать

К. Шеннон предложил также и метод такого кодирования, который получил название статистического, или оптимального кодирования. В даль-

нейшем идея такого кодирования была развита		в работах Р. Фано и
			И
Д. Хаффмена и в настоящее время широко используется на практике для
«cжатия сообщений».		У
2-я теорема (для каналов связи с помехами):	Г
Если пропускная способность канала равна
	C ,	а производительность

и с вероятностью ошибки, сколь угодно близкой к нулю. Если же R( x ) C ,

источника R( x ) C , то путѐм соответствующего кодирования можно пере-
	Б
давать информацию по каналу связи со с оростью, сколь угодно близкой к C
а
к

то можно закодировать источник та им образом, что ненадѐжность будет
	т
меньше, чем R( x ) C , где – сколь угодно малая величина.
Не существует способа кодированияе		, обеспечивающего ненадѐжность,
о
меньшую, чем R( x ) C .
и

К сожалению, те рема К. Шеннона для каналов с шумами (помехами)

указывает только на в зм жн сть такого кодирования, но не указывает способа построениялсоответствующего кода.

и3.8.бЭнтропия непрерывного источника случайной величины и еѐ

свойства

БДля нахождения энтропии непрерывного источника воспользуемся выражением для энтропии дискретного источника, заменив вероятности P( x )

на элементарные вероятности W( x )dx , где W( x ) – плотность распределения вероятности информационного сигнала источника. В результате получим


H( x ) W ( x )dx log2 W ( x )dx
		(3.28)
		(3.28)

W ( x ) log2 (W ( x ) log2 ( dx ) dx.

Логарифм бесконечно малой величины (dx) равен минус бесконечно-
сти, в результате чего получаем

H( x )	W( x )log2 W( x ) dx.	(3.29)

Таким образом, энтропия непрерывной случайной величины бесконеч-
		Р
но велика. Но так как в последнем выражении первое слагаемое ( ) от вели-
чины x или от W( x ) не зависит,		И
чины x или от W( x ) не зависит,	при определении энтропии непрерывной

величины это слагаемое отбрасывают, учитывая толькоУвторое слагаемое (некоторую «добавку» к бесконечности). Эта добавочная энтропия, опреде-

ляемая формулой										Г
										Г
										Б
				H( x )						Б	(3.30)
				H( x )			W( x )log2 W( x ) dx,				(3.30)
									а
									а
и называется дифференциальной энтропией непрерывной случайной величи-
ны (источника).								к
Как и для дискре ных сообщений, существуют следующие разновид-
ности дифференциальной эн ропии непрерывной величины.
Условная энтр пия случайной величины y относительно случайной
величины x .					т
величины x .				о
				о
		и
		и					W( x, y )log2 W( y / x ) dxdy.				(3.31)
			H( y / x )				W( x, y )log2 W( y / x ) dxdy.				(3.31)
	л
	л
Совместнаяб			энтропия двух непрерывных случайных величин равна
и
и			H( x, y )			W( x, y )log2 W( x, y ) dxdy.					(3.32)
Б
Б

Для дифференциальной энтропии справедливы все свойства простой энтропии.

Если случайная величина ограничена в объѐме V b a (может принимать значения только в интервале от a до b ), то еѐ дифференциальная энтропия максимальна при равномерном закона распределения этой величины:

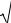
Hmax ( x ) log2( b a ).

(3.33)

Если случайная величина не ограничена в численных значениях (т. е. может изменяться в пределах от до ), а ограничена только по мощности, то дифференциальная энтропия максимальна в случае гауссовского закона распределения этой величины. Этот максимум соответствует величине

H	max	( x ) log	2	2 e 2	,	(3.34)
	max		2

где 2 – мощность случайной величины.			Р

Следовательно, энтропия зависит только от мощности 2 .
		И
Эта очень важная формула будет использоваться позднее для опреде-
ления пропускной способности непрерывного канала связи.
	У
Г
3.9. Пропускная способность непрерывного канала
Б
Сигнал, отображающий непрерывное сообщение, можно рассматривать

как некоторый случайный процесс, спектр которого ограничен определѐнной полосой частот. В соответствии с теоремой Котельникова для описания этого

характеризуется своими дискр тными значениями, то знание значений сиг-

процесса длительностью T	требуется N		T	отсчѐтов,	где t	1	– ин-
процесса длительностью T	требуется N		t	отсчѐтов,	где t	2F	– ин-
			t			2F
		а				max
тервал дискретизации. Так как сигнал с ограниченным спектром полностью
	к
	е

нала между этими значениями не увеличивает наших знаний о сигнале. Сле-

довательно, при определении эн ропии непрерывного сигнала достаточно

учитывать только его дискре ные значения, взятые в соответствии с теоре-
мой Котельникова.			т
Как было показано выше, энтропия обладает свойством аддитивности.
		о
Так, если у какого-то д скретного сигнала длительностью t энтропия равна
	и			элементов, будет равна
H( x ) , то энтропия сигнала, составленного из N
л
б

N H( x ). Аналогичным образом можно вычислить энтропию непрерывного

сигнала дл тельностью T , которая будет равна
и	N H1 (x) 2 Fmax T H1(x),	(3.35)
Б

где H1( x ) – энтропия одного сечения случайного сигнала, определяемая через одномерную плотность вероятности. Размерность энтропии H1( x ) – бит

на один отсчѐт случайного сигнала (одно сечение случайного процесса). Производительность непрерывного случайного процесса (источника)

будет равна

R( x )	H( x )	2 F	H	( x ).	(3.36)

	T	max	1

Таким образом, производительность эргодического источника непрерывного сигнала полностью определяется энтропией одного отсчета и удвоенной полосой частот генерируемого источником сигнала.

Если x( t ) – сигнал на входе канала связи, а y( t ) x( t ) n( t ) – сигнал на его выходе ( n(t) – аддитивный шум канала), то скорость передачи информации по непрерывному каналу связи будет определяться так:

C max R( x, y ) ,

(3.37)

R( x, y )

H y x

H( y ) H( y / x ) ,

Р(3.38)

где величину 1 /

надо заменить на 2Fmax . Предполагая, что

источник сиг-

нала согласован с каналом и его полоса пропускания F Fmax , имеем

R( x, y ) 2 F H( y ) H( y / x ) ,

(3.39)

где, как и ранее, H( y )

– это энтропия выходного сигнала канала связи;

H( y / x ) – энтропия шума (это

название

будет разъяснено далее по тексту).

Пропускная способность равна максимально возможной скорости пе-

редачи по каналу связи,

когда ис очник сигнала полностью согласован с ха-

рактеристиками канала связи:

H ( y) H ( y / x) .

C 2 Fmax

(3.40)

H( y ) достигается в случае гауссовского закона распреде-

Максимум

ления случайной ве ичины y . При этом

max H( y ) log2

(3.41)

2 e y ,

где 2

– мощность выходного сигнала канала связи.

При учѐте влияния помехи необходимо рассматривать наихудший слу-

чай, когда помеха распределена также по гауссовскому закону:

W ( n )

exp

(3.42)

2 n

где 2n – мощность шума, (тем самым гарантируется пропускная способность

канала не хуже определенной, при любых статистических характеристиках шума).

Условная вероятность W( y / x ) – это вероятность распределения случайной величины y при якобы известном заранее значении x , хотя величина x является случайной. Но так как y( t ) x( t ) n( t ) , можно записать

( y x )

W( y / x )

exp

(3.43)

2 n

Определим условную энтропию H( y / x ):

H( y / x )

W ( x, y )log2 W ( y / x ) dxdy

W ( x ) W ( y / x )log2 W ( y / x ) dydx

(3.44)

W ( x )log

2 e 2

H( n ).

почему

Отсюда видно,

условная энтропия

H( y / x ) называется энтро-

пией шума.

Осуществ в не бх димыетподстановки, получаем следующее выраже-

ние для пропускной способности канала связи:

C 2 F log

F log

(3.45)

Учитывая, что рассматриваемые случайные процессы

x( t ) , n( t ) и

y( t ) x( t ) n( t )

являются гауссовскими,

мощность выходного процесса

y(t) определяется как

сумма

мощностей

его

аддитивных

составляющих

2y 2x 2n . Тогда выражение для пропускной способности будет иметь вид (формула Шеннона)

			2
C F log	2	1	x	F log	2	1 q .	(3.46)
C F log		1	2	F log		1 q .	(3.46)
			2
			n

где q	2	P
	x	s	– отношение мощности сигнала к мощности шума в канале
	2	P	– отношение мощности сигнала к мощности шума в канале
	2	P
	n	n
связи.
В заключение можно отметить следующее. Для достижения скорости

передачи информации по непрерывному каналу связи, близкой к пропускной способности канала связи, сигнал x(t) по статистической структуре должен

3.10. Предельные информационные характеристики канала связи

Преобразуем формулу Шеннона следующим образом:

E C

C F log

F log

(3.47)

где Eb Ps / C – энергия, приходящаяся

один бит передаваемой информа-

на

ции; N0 Pn / F – спектральная плотность мощности аддитивного шума,

действующего в канале связи.

Выполним ряд преобразованийе.

EbC

(3.48)

тlog2 1

N0 F

(3.49)

log2 1

(3.50)

Окончательно получим нижнюю границу отношения

, при которой

возможна

реализация заданной

спектральной эффективности

(бит/с)/Гц,

канала связи

быть близок к флюктуационной помехе (шуму) с гауссовским законом распределения.

Eb 2 1 .

Рассмотрим канал связи при условии F . Перепишем формулу Шеннона следующим образом:

					EbC		N0 F
	Eb				EbC		EbC
1								.	(3.51)

		log2 1
	N0				N0	F			Р

			1 )x
Учитывая, что lim (1				e ,					И
Учитывая, что lim (1				e ,		получим минимально возможное отно-
x			x

шение энергии, приходящейся на один бит передаваемой информации, к спектральной мощности шума, при котором еще возможна передача информации.

ln( 2 ) 0,69 .

(3.52)

log2( e )

Если рассмотреть полученную выше нижнюю границу для

, то в

случае

если 0 ,

т.

. Fа

или

C 0

получим

lim

ln( 2 ). Это означа т, что если

/ N

0,69 ,

передача ин-

вности

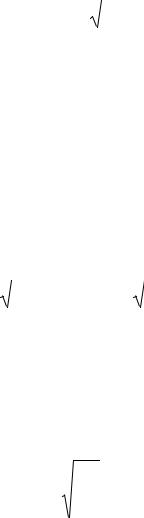
формации невозможна. На рис. 3.3 приведена зависимость минимального

требуемого отношения энергии, приходящейся на один бит передаваемой
			и
информации, к спектральнтй плотности шума для обеспечения заданной
		л
спектральной эффект				передачи информации.
	б
и
Б

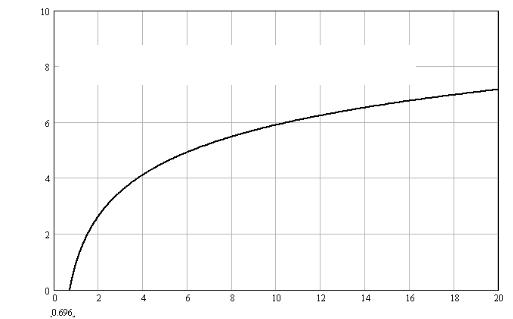
С/ F

Область запрещенных (нереализуемых) значений

						Р
						ИN
					Г		Eb
					Г			0
					Б			0
					Б
Рис. 3.3. Соотношение между спектральной эффективностьюУ								и требуе-
мым минимальным отношением сигнал/шум
3.11. Расширение границы Шеннона (BLAST – Bell Labs Layered
Space Time)				к
			е
Как известно, пропускная способностьаканала связи с ограниченной
полосой частот удовлетворяет сл дующ му соотношению:
		от
C F log2	1 q , бит/с,
		о
где F – ширина п л сы час				канала; q – мощности сигнала к мощности
шума в канале		. Является ли данная граница непреодолимой?
Рассмотр м структурную схему системы передачи информации, при-
л
веденную на р с. 3.4.
б

Передаваемыйсвязипоток данных разбивается на несколько параллельных

потоков (чис о потоков равно n ). Далее каждый из полученных параллельныхипотоков подвергает модуляции свой радиосигнал. Радиосигналы всех Бпараллельных потоков отличаются только модулирующими символами (совпадают схемы модуляции, интервалы излучения, используемые коды канала, центральные частоты, уровни и пр.) Каждый из полученных радиосигналов излучается в пространство своей антенной (антенны имеют пространственное разнесение).

На приемной стороне организуется m приемных каналов (по числу используемых разнесенных в пространстве антенн). Всегда m n . Сигналы принятых каналов подвергаются специальной обработке, заключающейся в операции, обратной той, которой они подверглись в среде распространения

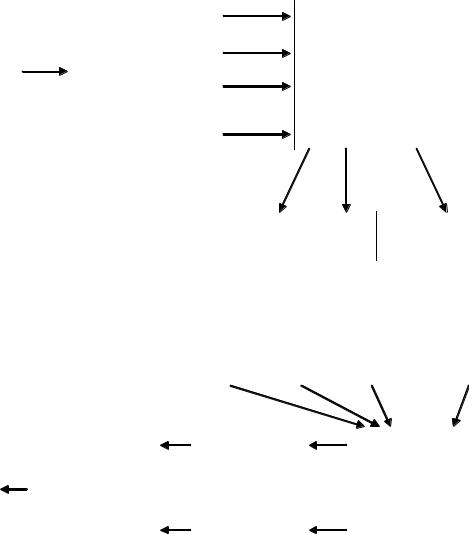
( K( j ) матрица n m, элементы которой представляют собой комплексные

коэффициенты передачи между i-й передающей и j-й приемной антеннами).
Таким образом, вектор принимаемых сигналов Srx Srx1 ,...,Srx m мож-
но записать следующим образом:
Srx StxK(jω ),	(3.53)

где Stx Stx1 ,...,Stx n – вектор сигналов, сформированных модулятором передающей части.

С учетом операции «Компенсация канала» имеем вектор сигналов на

входе демодулятора

Sdem SrxK(jω ) 1

StxK(jω )K(jω ) 1

Stx .

(3.54)

Источник

информации

Демультиплексор

Модулятор

Dn .

…

Ант.1

Ант.2 …

Ант.n

СРЕДА РАСПРОСТРАНЕНИЯ

[К(j )]

Ант.1

Ант.2

Ант.3

…

Ант.m

…

D1*

Компенсатор

Потребитель

Мультиплексор

Демодулятор

канала

информации

[К(j )]-1

Dn*

Рис. 3.4. Структурная схема, поясняющая сущность BLAST технологии

делить (на основании свойства аддитивности информации) как

Таким образом, на входе демодулятора (соответственно на его выходе) имеем копии передаваемых сигналов или данных.

Сравним приведенную выше систему с обычной системой связи, использующей только один канал на передачу и прием. Для сравнения будем считать, что отношение q в обеих системах одинаково. Это означает, что в

каждом канале «разнесенной» системы отношение сигнал/шум будет в n раз меньше q / n . Таким образом, общую пропускную способность можно опре-

	n F log		q	,	(3.55)
Cразнес.		2 1
Cразнес.		2 1
			n
а для обычной системы имеем
Cнеразнес. F log2 1 q .					(3.56)
					Р

На рис. 3.5 приведены графические зависимости УпотенциальногоИ выигрыша в пропускной способности системы, построенной по BLAST техноло-

гии, по сравнению с обычной системой связи ( n 1) от отношения q при

различном числе каналов n разнесенной передачи информации.
Из рис. 3.5 видно, что применение технологииГBLAST может увеличи-
			а
вать пропускную способность системы связи в разы при сохранении спек-
тральных и энергетических характеристик к нБла связи. Есть ли противоре-
		к
чия в полученном результате? Рассмотрим процедуру «компенсации канала»:
	е
	K(jω )K(jω ) 1 I ,			(3.57)
т
где I – единичная ма рица разм ром n n . Другими словами,				правильно
о
осуществленная процедура «компенсации канала» эквивалентна реализации

n параллельных независимых каналов. Так что полученный результат вполне адекватен и не речит сновным положениям теории информации. Так

за счет чего возн кает выигрыш без дополнительных энергетических и спек-
тральных затрат?
		против
		л
	б
и
Б

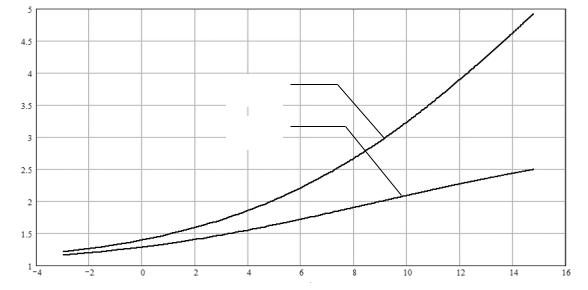
Сразнес/Снеразнес.

n=16

n=4

		Р
	И
Г	q, дБ
Г
Рис. 3.5. Потенциальный выигрыш в пропускной способности
Б

Если внимательно присмотреться к приемной частиУ, то можно интер-

претировать совокупность из m приемных антенн и компенсатора канала как

антенную решетку, реализующую n своеобразных пространственных лучей,
		а
которые как бы собирают энергию, излуч емую каждой передающей антен-
ной в различные направления (а не	только		в н правлении на приемную си-

стему). Это можно еще интерпретиров ть			собирание всевозможных про-
е

странственных лучей, вызываемых п р отражениями, преломлениями и прочими эффектами распространения радиоволн. Именно за счет такого сбора «рассеянной» энергии и получа тся выигрыш в пропускной способности.

Данное утверждение	верждае ся тем, что в условиях свободного распро-
странения радиоволн ма рица		K(jω ) становится сингулярной (определитель
равен нулю) и нахожден е братной матрицы становится невозможным.
Сложность пр менения технологии BLAST заключается в возможно-
	под
сти и точности опреде ен я матрицы комплексных коэффициентов передачи
каналов K(jω ). Существеннаяи		нестационарность среды распространения ра-

диоволн бнеолходимость точного оценивания фазовых соотношений в данной матр це являются сдерживающим фактором повышения пропускной способности. Объем обучения алгоритма «компенсации канала» накладывает

огранБичен я на количество параллельных каналов на передающей стороне и может полностью нивелировать реализуемый выигрыш в пропускной способности. Необходимо отметить, что к настоящему времени для реализованных опытных образцов каналов передачи информации с BLAST-технологией, полученные выигрыши едва превышают значения, равные двум. При этом сложность и стоимость имеющихся BLAST решений сдерживает их широкое практическое внедрение.

<<< < Предыдущая 1 23 / 103 4 5 6 7 8 9 10 > Следующая >>>

Соседние файлы в предмете Сотовые сети

#
15.12.20182.46 Mб256Гельгор, Попов - ТЕХНОЛОГИЯ LTE МОБИЛЬНОЙ ПЕРЕДАЧИ ДАННЫХ.pdf
#
15.12.20181.15 Mб52ИССЛЕДОВАНИЕ ФИЛЬТРОВ НА ПАВ .doc
#
15.12.20184.98 Mб227лекции Сети и системы телекоммуникаций 2013.pdf
#
15.12.20181.49 Mб93лекция 3G .pdf
#
15.12.20181.27 Mб59Лисечко - Посібник LTE, 2014.pdf
#
15.12.201810.45 Mб90Листопад - Теоретические основы цифровой радиосвязи, (2012).pdf
#
15.12.2018629.68 Кб77лк Распространение радиоволн в системах мобильной связи .pdf.pdf
#
15.12.20181.07 Mб60метода РАЗРАБОТКА ТЕРРИТОРИАЛЬНОЙ МОДЕЛИ 2013.pdf
#
15.12.20183.2 Mб165метода Теор.осн.сист.моб.связи (2012).doc
#
15.12.2018561.15 Кб48му Алгоритмы речевого кодирования GSM. 2006.doc
#
15.12.20184.53 Mб155Обзор системы GSM dnl2601.pdf

3.4. Избыточность источника

3.6. Совместная энтропия двух источников

3.7. Скорость передачи и пропускная способность канала связи