§ 2.2. Дифференциальная игра: общее решение
Дадим вначале
некоторые комментарии по вопросу
существования решения задачи. Предполагая,
что функции
,
достаточно гладкие,
,
введем функцию стоимости игры
, (2.3)
где
дифференцируемая функция при любых
допустимых стратегиях игроков
.
Уравнение Гамильтона-Якоби будет иметь
вид
(2.4)
Здесь
−
гамильтониан
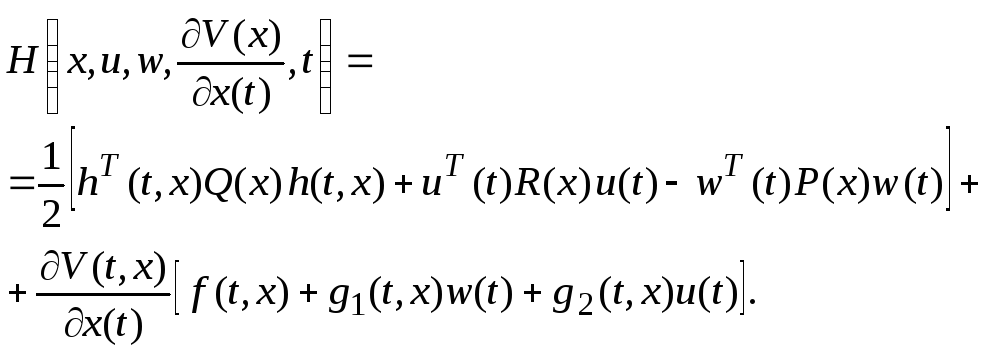(2.5)
При незаданном
времени окончания переходного процесса
(задача стабилизации), т.е. при
и
,
учитывая, что
в явном виде не зависит от времени, будем
иметь
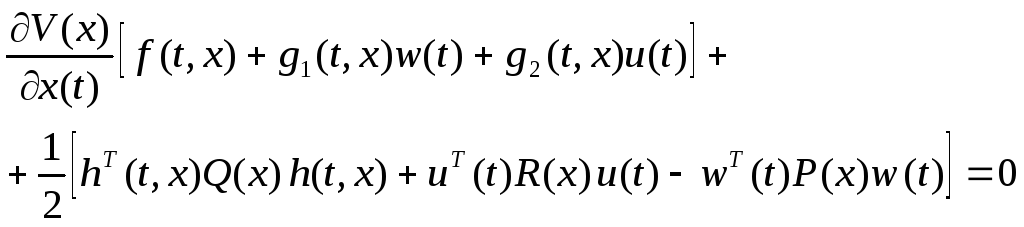(2.6)
с
граничным условием
,
так как
.
Перепишем (2.6) в виде
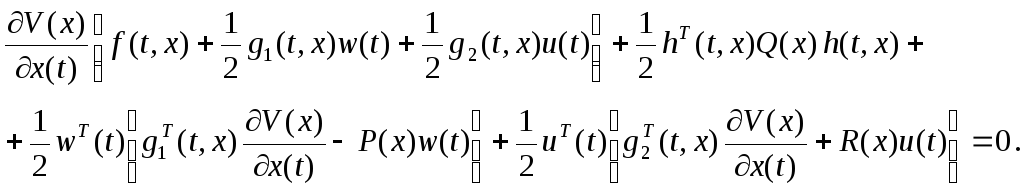(2.7)
Определим управления
и
с точностью до
так, чтобы последние два слагаемых (2.7)
равнялись нулю, т.е.
. (2.8)
Тогда уравнение Гамильтона-Якоби примет вид
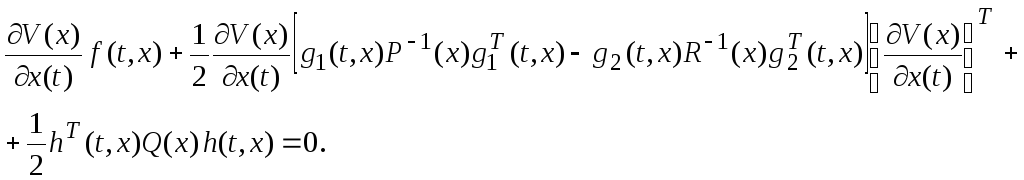(2.9)
Исходная система с управлениями (2.8) определяется выражением
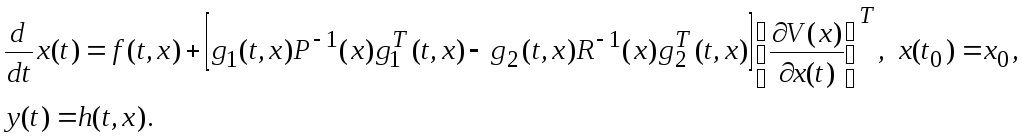
Отметим, что при
, (2.10)
уравнение (2.9) вместе с канонической системой
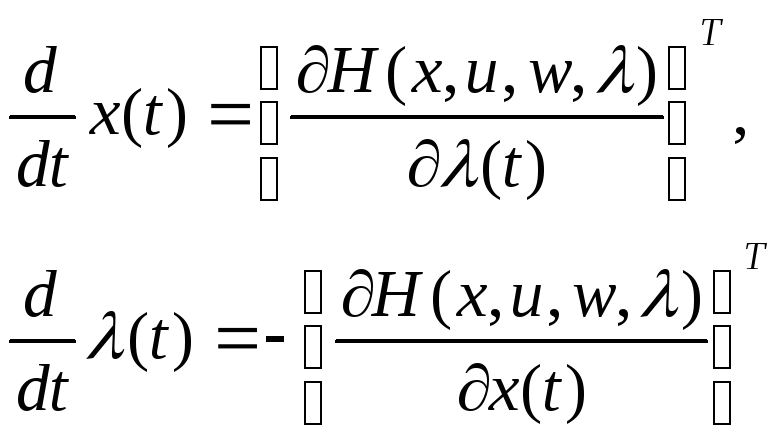
образуют необходимые условия оптимальности системы (2.1) с управлениям
. (2.11)
Как будет показано
дальше, матрицы
и
,
при всех
и параметрах системы
и
,
должны назначаться так, чтобы матрица
(2.12)
была бы положительно полуопределенной.
Очевидно, что для реализации управлений вида (2.8) необходимо решить уравнение (HJ) в частных производных, что является самостоятельной сложной задачей.
Кроме того,
1.
может и не существовать;
2. если и можно
найти
,
то нет гарантии, что функция времени
- градиент
,
вычисленный в точке
,
есть дополнительный вектор
,
соответствующий
и
т.е. нет уверенности, что существует
зависимость
(2.13)
Пусть
,
где Х – область, содержащая S.
Обозначим минимум (наибольшую нижнюю
границу) функции
через
:
.
(2.14)
Управления
,
при котором достигается
,
обозначим через
.
Таким образом,
- допустимые и в силу (2.14) оптимальные
управления.
Предположим также:
1.
для
2.
непрерывно дифференцируема на X.
В
силу оптимальности
можно записать, что:
(2.15)
для
Таким образом, при предположениях 1 и 2
уравнение (2.15) является дополнительным
необходимым условием оптимальности.
Если на правом
конце задано условие
,
то
(2.16)
и
вектор
,
удовлетворяет следующему соотношению:
Покажем, что при некоторых предположениях относительно управляющих воздействий, справедлива зависимость (1).
Лемма 2.2.1
Пусть имеются
допустимые управления
и при этом:
-
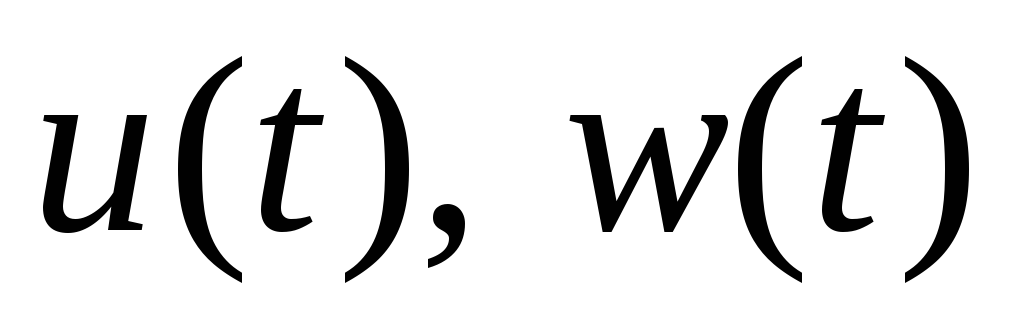переводят
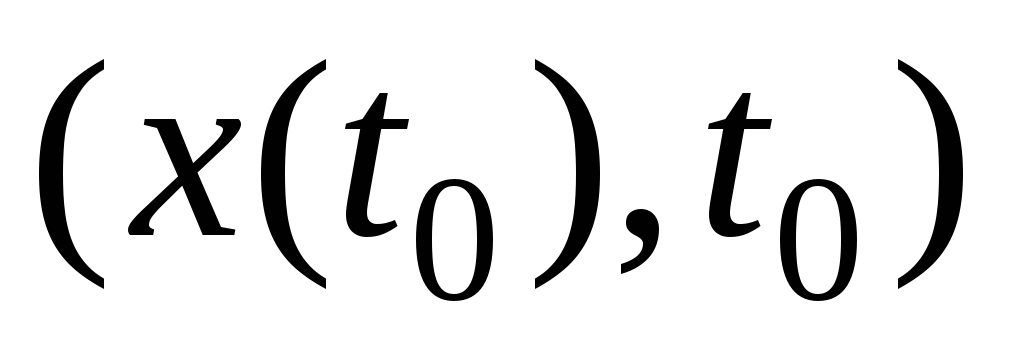в S; -
имеется траектория
,
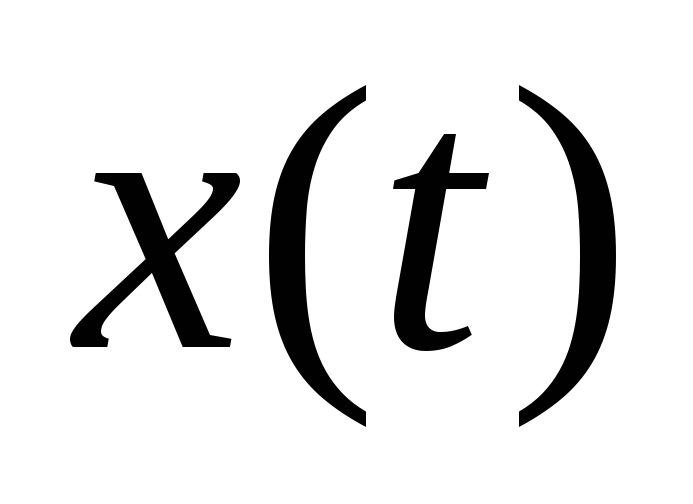соответствующая
,
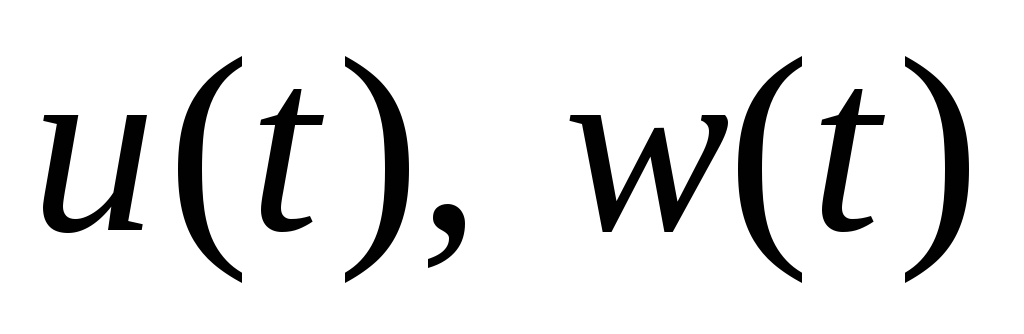то
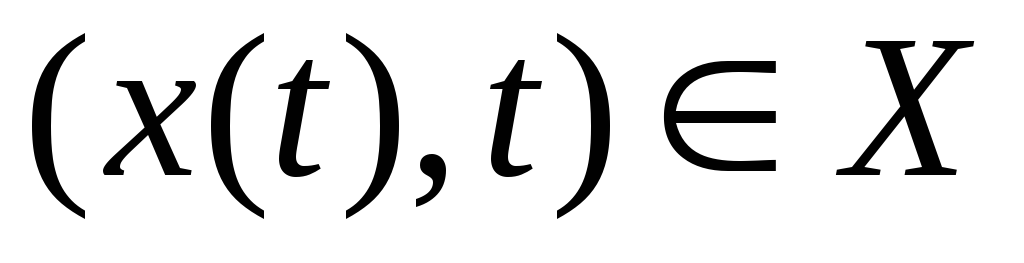для всех
; -
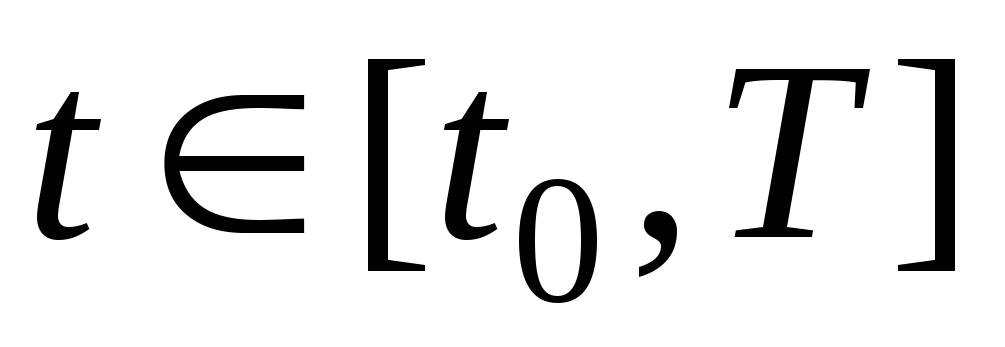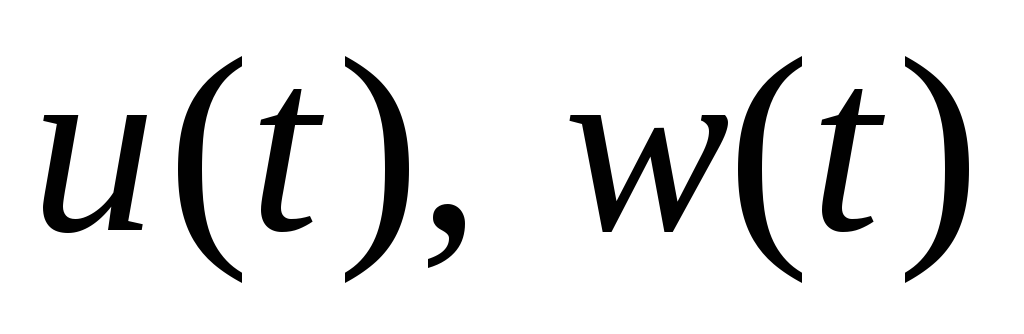удовлетворяют
соотношению
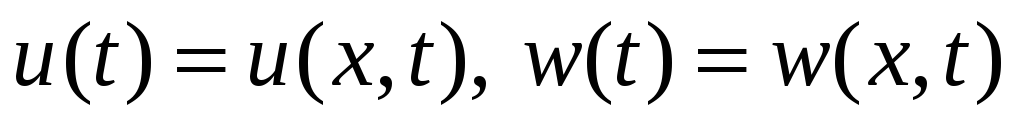для всех
,
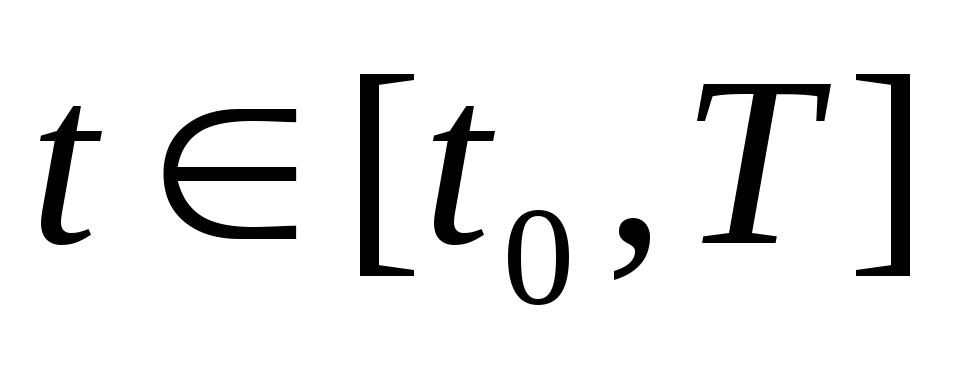где
являются решением уравнения
Гамильтона-Якоби, то
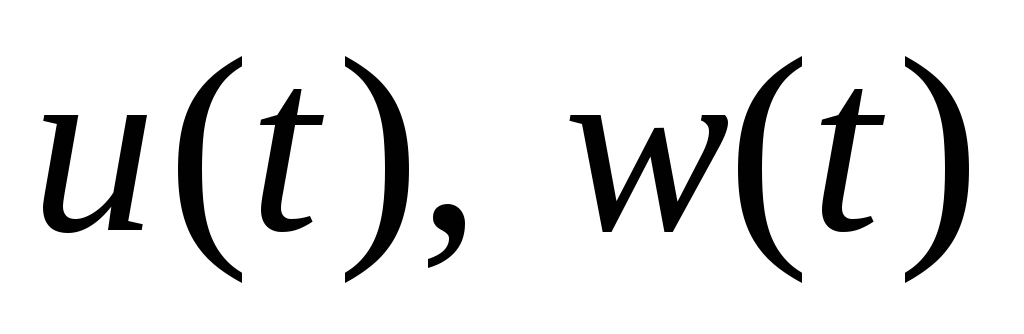есть оптимальные управления к множеству
допустимых управлений, производящих
траектории, которые целиком расположены
в X ,
тогда
.
Доказательство
Для сокращения записи введем обозначение
,
.
Тогда
, (2.17)
и
(2.18)
Продифференцируем
выражение (2.18) по
.
Будем иметь
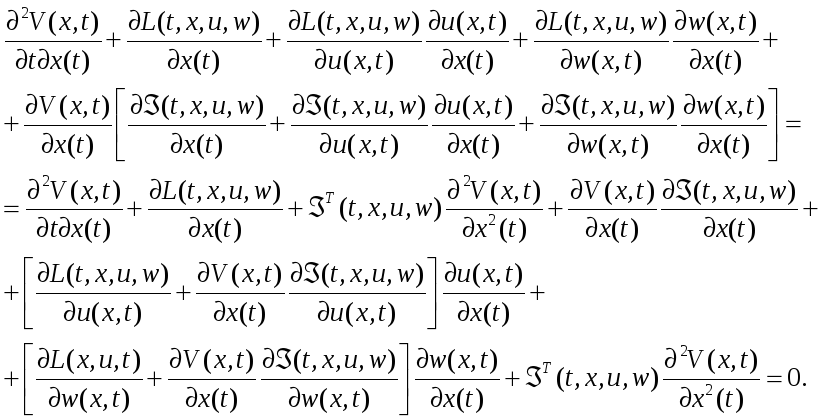(2.19)
Выражения
в квадратных скобках при
на оптимальной траектории обращаются
в нуль. Используя (2.19), преобразуем (2.18)
к виду
(2.20)
Кроме
того, условие (2.16) определяет значение
.
Отметим, что уравнение (2.20) совместно с
уравнением (2.16) образует систему уравнений
Эйлера – Лагранжа.
Таким образом,
если имеются допустимые управления
и при этом:
-
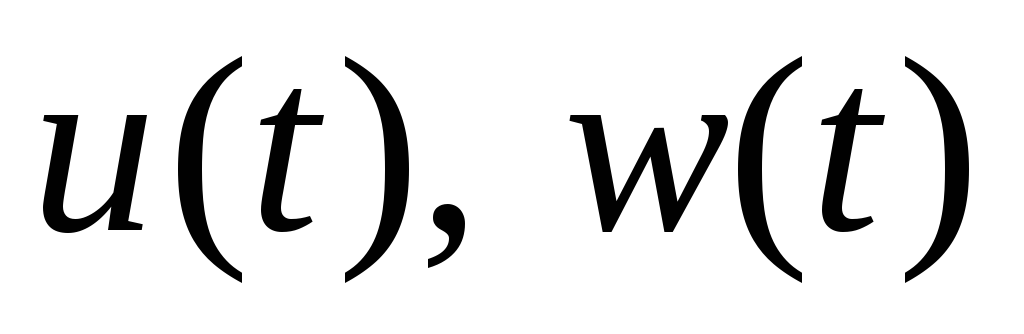переводят
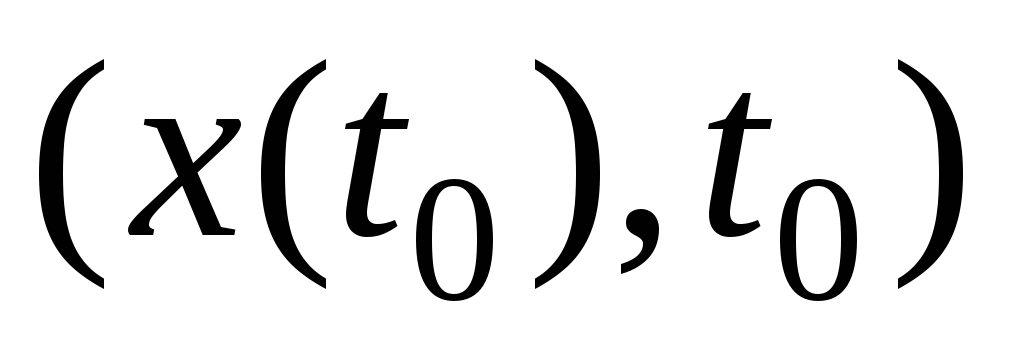в S; -
имеется траектория
,
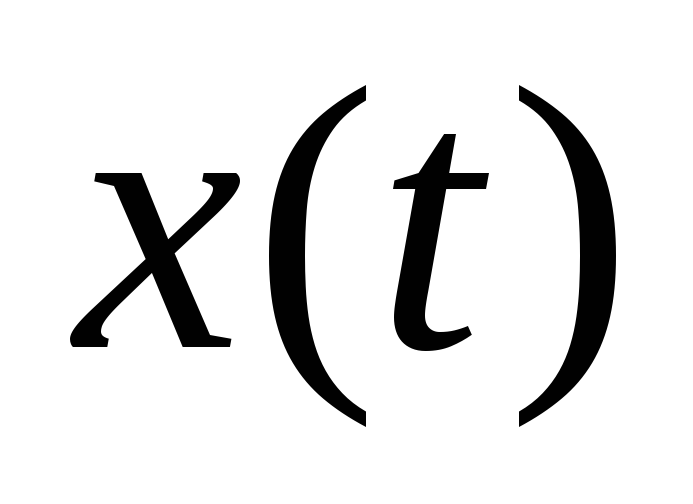соответствующая
,
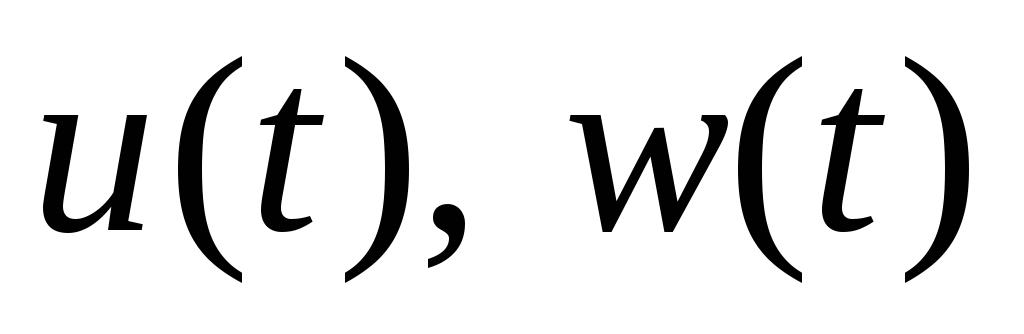то
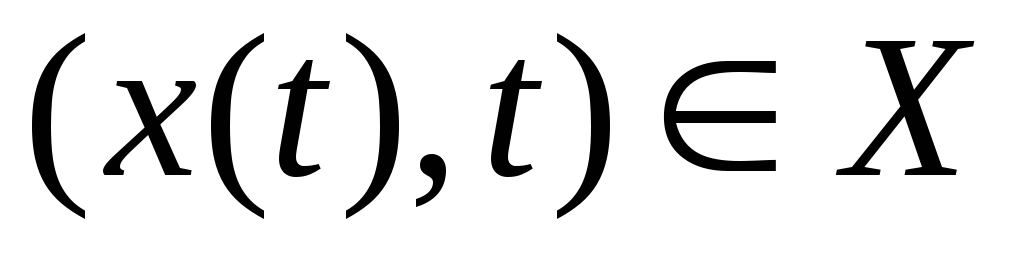для всех
; -
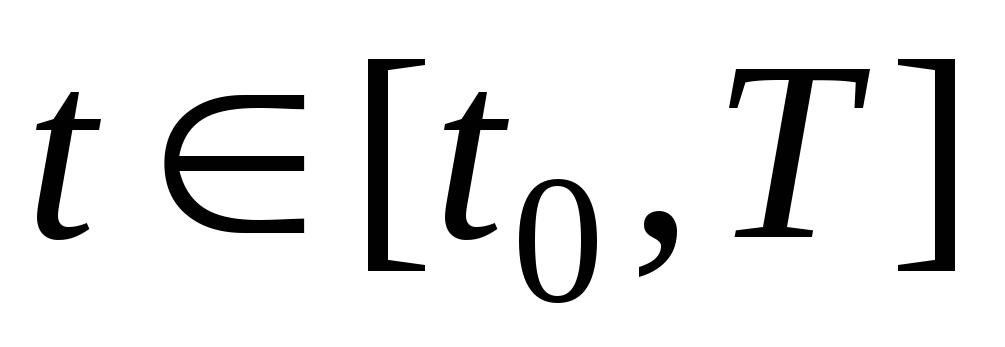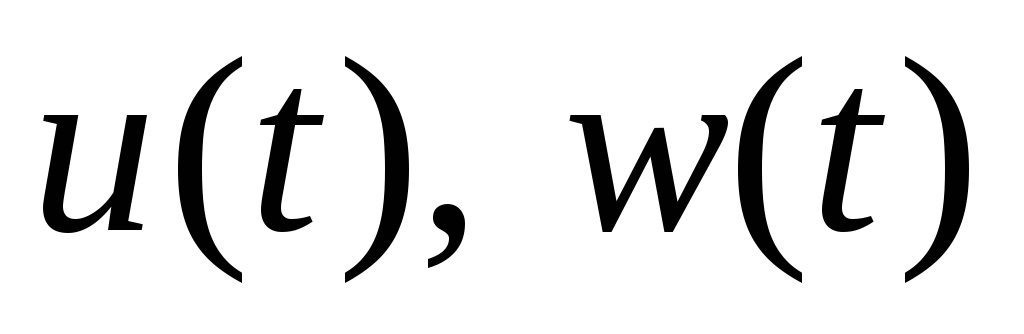удовлетворяют
соотношению
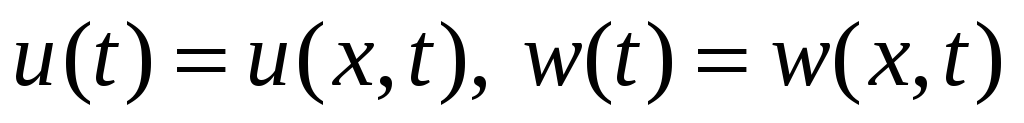для всех
,
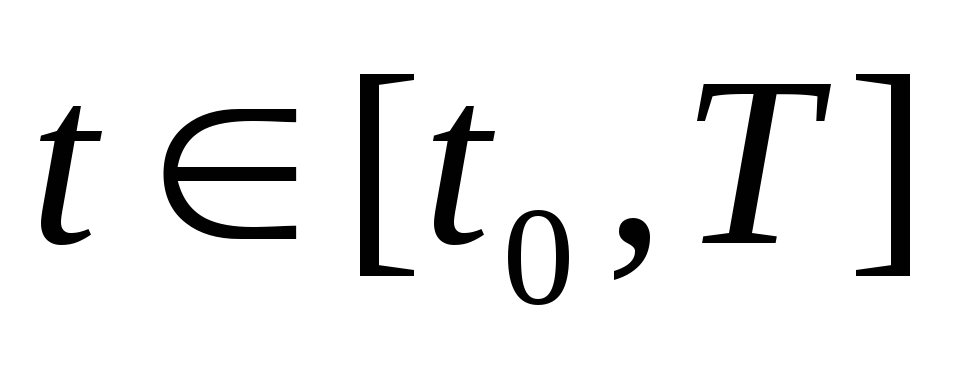где
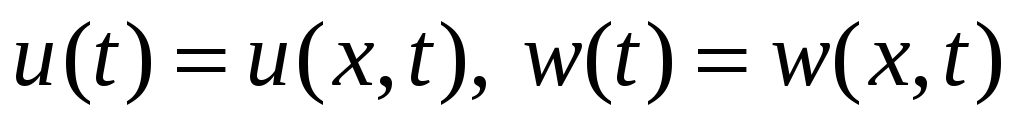являются решением уравнения
Гамильтона-Якоби, то
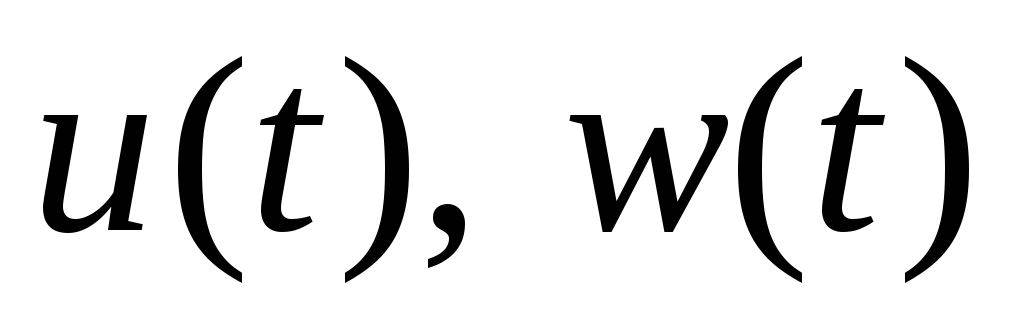есть оптимальные управления к множеству
допустимых управлений, производящих
траектории, которые целиком расположены
в X .
Рассмотрим каждое из составляющих необходимых условий оптимальности.
1.
Первое уравнение (для
)
канонической системы
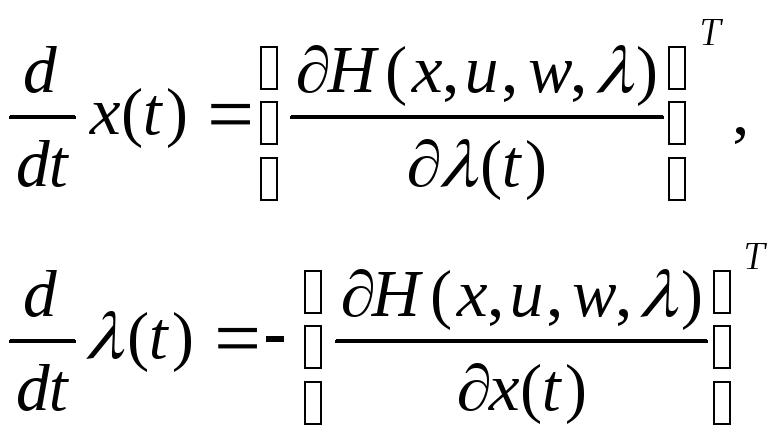
есть
в точности исходная система уравнений,
описывающая объект управления, которая
не зависит от дополнительной переменной
.
Второе уравнение (для
)
канонической системы описывает движение
нормали к гиперплоскости вдоль оптимальной
траектории. Уравнение имеет множество
решений, каждое из которых описывает
движение соответствующей нормали к
гиперплоскости вдоль оптимальной
траектории. Каноническая система имеет
решения вдоль любой траектории системы,
а не только для оптимального управления.
2.
Первое свойство дополнительной
переменной
состоит в том, что оптимальное управление
является точкой стационарности
гамильтониана (2.5).
3. Формулировка необходимых условий не зависит от типа области S значений конечных состояний системы и от того, фиксировано или нет время окончания переходного процесса.
4. Необходимые условия оптимальности, сформулированные в виде поведения гамильтониана на оптимальной траектории, непосредственно зависят от того, является ли время окончания переходного процесса фиксированным или нет. Гамильтониан постоянен вдоль оптимальной траектории лишь в случае, когда система и функционал явно не зависят от времени.