
- •1.Определенный интеграл.
- •1.1.Определение первообразной. Неопределенный интеграл и его свойства. Интегралы от элементарных функций.
- •2. Определенный интеграл.
- •2.2. Замена переменной. Интегрирование по частям.
- •2.3. Интеграл с переменным верхним пределом.
- •2.4. Приближенное вычисление определенного интеграла.
- •2.5. Понятие о несобственных интегралах.
- •Площадь плоской фигуры
- •Тригонометрическая и показательная формы
- •Следствие
- •Доказательство
- •5. Функция нескольких переменных.
- •5.1. Определение функции нескольких переменных. Область определения и множество значений. Непрерывность. Частные производные полный дифференциал. Экстремумы.
- •5.2. Подбор эмпирических формул с помощью метода наименьших квадратов.
- •6.1. Дифференциальное уравнение n-го порядка. Общее и частное решение. Задача Коши. Краевая задача.
- •6.2. Дифференциальные уравнения первого порядка. Уравнения вида и .Уравнения с разделяющимися переменными. Однородные уравнения. Линейные дифференциальные уравнения первого порядка.
- •6.3. Использование дифференциальных уравнений первого порядка при решении некоторых биологических задач(задача о росте численности популяций, задача о переводе вещества в раствор).
- •6.6. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами.
- •7 Элементы теории вероятностей.
- •7.1 Достоверное, невозможное и случайное событие. Классическое определение вероятности реализации некоторого события. Статистическое определение вероятности. Геометрическая вероятность.
- •7.2 Совместные и несовместные события. Полная группа событий. Сумма событий. Вероятность суммы событий.
- •7.3 Зависимые и независимые события. Произведение событий. Условная вероятность. Вероятность произведения событий.
- •7.4 Формула полной вероятности. Формула Бейеса вероятностей гипотез.
Доказательство
Самое простое доказательство этой теоремы даётся методами комплексного анализа. Используется тот факт, что функция,аналитическая на всей комплексной плоскости и не имеющая особенностей на бесконечности, есть константа. Посему, функция 1/p, где p — многочлен, должна иметь хоть один полюс на комплексной плоскости, а, соответственно, многочлен имеет хоть один корень.
5. Функция нескольких переменных.
5.1. Определение функции нескольких переменных. Область определения и множество значений. Непрерывность. Частные производные полный дифференциал. Экстремумы.
Если в каждой точке М из множества {м}, м-мерного пространство Ем ставится в соответствии некоторое число u, то говорят что на множестве {м} задана функция u=u(м) или u=f(м). Множество {м} – областью задания функции. Число n соответствующая в данной точке М из множества {м} будем называть частным значением функции в точке М. В совокупности всех частных значений функций или u=f(м) множество значений функций. т.к. точка М определяется м координатами Х1,Х2…Хм, то для функции или u=f(м) м переменных используются также обозначения или u=f(Х1,Х2…Хм).
Замечание: всякая функция от нескольких переменных становится функцией от меньшего числа переменных, если часть переменных зафиксировать, т.е. придать постоянные значения. Например: пусть мы имеем функцию u=f(X, Y, Z). Если предположить, что Z сохраняет постоянное значение Z=c, то мы получим функцию от двух переменных X и Y: u=f(X, Y, с). Далее, предполагая, что две переменные Y и Z сохраняет неизменные значения Y=b, Z=c, то получим функцию u=f(X, b, c)от одной переменной.
Определение 1: если f(x, y) называется непрерывной в точке (x0, y0), если: 1) функция определена в данной точке и эта точка является предельной для области существования функции; 2) бесконечно малым приращениям ∆х0=х-х0, ∆у0=у-у0 переменных х и у соответствует бесконечно малое приращение f(x0, y0) функции f(x, y), т.е. при любом способе стремления приращений ∆х0 и ∆у0 к нулю, для которых f(х+х0,у+у0) имеет смысл, выполнено условие:
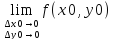 =
=
 =0.
=0.
Определение 2: функция f(x, y) называется непрерывной в данной области, если эта функция непрерывна в каждой точке рассматриваемой области, т.е. если для каждой точки (x, y) области имеем:
 =
=
 =0, причем здесь мы предполагаем, что
смещенная точка
=0, причем здесь мы предполагаем, что
смещенная точка
 принадлежит данной области и
принадлежит данной области и
 существует. Таким образом, можно сказать,
что функция непрерывна тогда и только
тогда, когда бесконечно малым приращениям
ее аргументов соответствует бесконечно
малое приращение функции.
существует. Таким образом, можно сказать,
что функция непрерывна тогда и только
тогда, когда бесконечно малым приращениям
ее аргументов соответствует бесконечно
малое приращение функции.
Определение: частной производной функции от нескольких переменных по одной из этих переменных называется предел отношений соответствующего частного приращения функции к приращению рассматриваемой независимой переменной при условии, что последнее стремиться к нулю.
Пусть
дана функция z=f(x,
y),
которая определена в некоторой
окрестности этой точки. Рассмотрим
отношение частного приращения ∆Хz=f(х
+ ∆х, у)-f(х,
у), функции z
по переменной х к приращению ∆х этой
переменной:
 .
.
Предел
этого отношения при ∆х, стремяшемся к
нулю называется частной
производной функции
z=f(x,
y)
по х и обозначается так:
 Следовательно
Следовательно
 .
Аналогично определяется частная
производная
.
Аналогично определяется частная
производная
 от
функции х=f(x,
y)
по у:
от
функции х=f(x,
y)
по у:
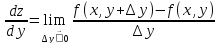 .
Заметим, что если от функции z=f(x,
y)
берется производная
.
Заметим, что если от функции z=f(x,
y)
берется производная
 ,
то у считается постоянным; а если же
находится
,
то у считается постоянным; а если же
находится
 ,
то х считается постоянным.
,
то х считается постоянным.
Определение 1: под дифференциалом независимой переменной понимается приращение этой переменной, т.е. dx=∆x и dy=∆y.
Определение
2:
полным
дифференциалом функции
z=f(x,
y)
двуз независимых переменных х и у
называется главная линейная часть
полного приращения этой функции. Dz
= A∆x
+ B∆y.
∆z
– dz
=
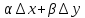 ,
где α,
β-
бесконечно малые. Функция имеющая
данный дифференциал данной области
называется дифференцируемой.
,
где α,
β-
бесконечно малые. Функция имеющая
данный дифференциал данной области
называется дифференцируемой.
Теорема 1: Дифференциал функции равен сумме произведения частных производных этой функции на дифференциалы соответствующих переменных. Док-во: пусть функция z=f(x, y) дифференцируема, т.е. имеет дифференциал Dz = A∆x + B∆y
Для
определения коэффициентов А и В напишем
полное приращение функции ∆z
= A∆x
+ B∆y
+α∆x
+β∆y,
где α
и β-бесконечно
малые при ∆х 0
и ∆у
0
и ∆у 0.
Полагая ∆у=0 в предыдущей формуле,
получим частное приращение ∆хz
= A∆x
+α∆x.
Отсюда
0.
Полагая ∆у=0 в предыдущей формуле,
получим частное приращение ∆хz
= A∆x
+α∆x.
Отсюда
 . и следовательно при ∆х
. и следовательно при ∆х 0
будем иметь
0
будем иметь
 .
Аналогично, полагая ∆х
.
Аналогично, полагая ∆х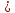 0,
находим
0,
находим
 .
Таким образом,
.
Таким образом,
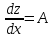 ,
,
 .
Подставив эти значения в формулу и
учитывая, что ∆х=dx
и ∆у=dy,
получим dz=
.
Подставив эти значения в формулу и
учитывая, что ∆х=dx
и ∆у=dy,
получим dz=
Теореме
2:
Достаточное условие дифференцируемости
функции. Если функция z=f(x,
y)
обладает непрерывными частными
производными
 и
и
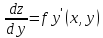 в данной области, то эта функция
дифференцируема в этой области и ее
дифференциал выражается формулой dz=
в данной области, то эта функция
дифференцируема в этой области и ее
дифференциал выражается формулой dz= .
.
Определение: максимумом функции f(x, y) называется такое значение f(x1, y1) этой функции, которое больше всех ее значений f(x, y), принимаемых данной функцией в точках некоторой окрестности точки (x1, y1). Минимумом функции f(x, y) называется такое значение f(x2, y2) этой функции, которое меньше всех ее значений f(x, y), принимаемых данной функцией в точках некоторой окрестности точки (x2, y2). Максимум или минимум функции f(x, y)называется экстремумами этой функции, а точка, в которой достигается экстремум, называется точкой экстремума.
Теорема:
в точке экстремума функции нескольких
переменных каждая ее частная производная
первого порядка либо равна нулю, либо
не существует. Док-во: рассмотрим функцию
двух переменных u=f(x,y)
и пусть f(x0,y0)-
ее максимум. Зафиксируем переменную
у, полагая у=у0.
Тогда
получим функцию одной переменной
u1=f(x,y0),
которая будет иметь максимум при х=х0.
От сюда на основании теории экстремума
функции одной переменной получаем, что
 или
или
 не существует. Таким же способом
доказывается, что
не существует. Таким же способом
доказывается, что
 или
или
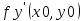 не
существует.
не
существует.
Замечание 1: точку, в которой частные производные первого порядка некоторой функции либо равны нулю, либо не существуют, называют критической для этой функции. Тогда теорема эквивалентна утверждению: экстремумы функции нескольких переменных могут достигать лишь в критических точках ее.
Замечание 2: введенные выше условия экстремума функции не являются достаточными, т.е. если, например, в некоторой точке все частные производные первого порядка функции равны нулю, то в этой точке функция не обязательно имеет экстремум.
