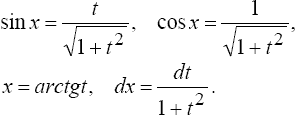1.Определенный интеграл.

1.1.Определение первообразной. Неопределенный интеграл и его свойства. Интегралы от элементарных функций.

Первообра́зной данной функции f называют такую F, производная которой (на всей области определения) равна f, то есть F ′ = f. Вычисление первообразной заключается в нахождении неопределённого интеграла, а сам процесс называется интегрированием.

Неопределенным интегралом называется функция F(x) + C, содержащая произвольное постоянное C, дифференциал которой равен подынтегральному выражению f(x)dx, т.е. или Функцию F(x) называют первообразной функции f(x) . Первообразная функции f(x) определяется с точностью до постоянной величины.

Свойства неопределённого интеграла:

Если функция f ( x ) имеет первообразную на промежутке X, и k – число, тоКороче: постоянную можно выносить за знак интеграла.

Если функции f ( x ) и g ( x ) имеют первообразные на промежутке X , тоКороче: интеграл суммы равен сумме интегралов.

Если функция f ( x ) имеет первообразную на промежутке X , то для внутренних точек этого промежутка: Короче: производная от интеграла равна подынтегральной функции.

Если функция f ( x ) непрерывна на промежутке X и дифференцируема во внутренних точках этого промежутка, то:

Короче: интеграл от дифференциала функции равен этой функции плюс постоянная интегрирования.

Интегралы от элементарных функций:

1.2.Некоторые приемы интегрирования: замена переменной; интегрирование по частям; интегрирование дроби, знаменатель который является квадратным трехчленом; интегрирование выражений, содержащих тригонометрические функции.

Формула замены переменной. Пусть имеет смысл сложная функция , где Х изменяется на некотором интервале. Тогда (1.3)

(В левой части после вычисления интеграла сделана подстановка .) Для доказательства обозначим через F(u) некоторую первообразную для f(u) и через G(x) -- первообразную для . Это означает, что и . Доказываемое равенство (1.3) эквивалентно тогда такому: или Для доказательства последнего соотношения достаточно проверить. что совпадают производные левой и правой частей. Но по формуле производной сложной функции получаем: то есть то же, что и . Формула (1.3) доказана. Заметим, что выражение в правой части (1.3) есть не что иное, как дифференциал du(x) функции . Так что мы можем записать (1.3) в виде

Теперь, после этого доказательства, мы получили право трактовать в обозначении неопределённого интеграла как некоторый дифференциал, а не просто как элемент обозначения интеграла, вроде скобки.

Формула интегрирования по частям. Пусть функции f(x) и g(x) имеют производную на рассматриваемом интервале изменения x . Тогда верно равенство (1.5) Эта формула называется формулой интегрирования по частям. Она позволяет "перебрасывать" производную с функции g(x) , стоящей под знаком интеграла, на другой подынтегральный множитель f(x) . При этом в правой части равенства появляется внеинтегральный член f(x)g(x) .

Пусть F(x) -- первообразная для и G(x) -- первообразная для . Тогда равенство (1.5) можно записать в виде

где G-- некоторая постоянная. Докажем, что производные левой и правой частей совпадают. По определению, . С другой стороны,

то есть производные совпадают, и формула (1.5) доказана. Мы видим, что она является следствием формулы для производной произведения.

Вводя обозначения и и замечая, что и , мы можем записать формулу интегрирования по частям в виде .

Интегрирование рациональных дробей:

Неопределенный интеграл от любой рациональной дроби на всяком промежутке, на котором знаменатель дроби не обращается в ноль, существует и выражается через элементарные функции, а именно он является алгебраической суммой суперпозиции рациональных дробей, арктангенсов и рациональных логарифмов. Сам метод заключается в разложении рациональной дроби на сумму простейших дробей. Всякую правильную рациональную дробь , знаменатель которой разложен на множители

можно представить (и притом единственным образом) в виде следующей суммы простейших дробей:

где Aij,αlt,βlt — некоторые действительные коэффициенты, обычно вычисляемые с помощью метода неопределённых коэффициентов.

Интегрирование тригонометрических функций:

1°. Интегралы вида

находятся с помощью тригонометрических формул

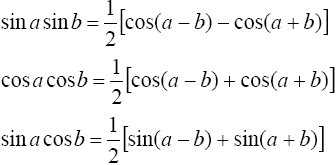
2°. Интегралы вида

где m и n - четные числа находятся с помощью формул понижения степени

Если хотя бы одно из чисел m или n - нечетное, то полагают (пусть m = 2k + 1)

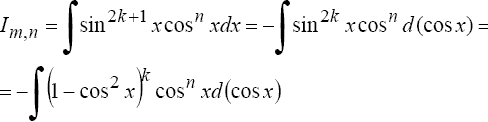
3°. Если m = -m, n = -l - целые отрицательные числа одинаковой четности, то

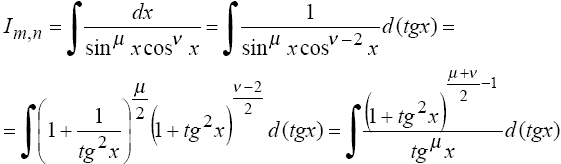
В частности, к этому случаю сводятся интегралы

4°. Интегралы вида

где R - рациональная функция от sinx и cosx, приводятся к интегралам от рациональных функций новой переменной с помощью подстановки при этом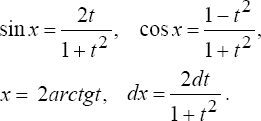

Если R{-sin x, cosx) = R(sinx, cosx), то целесообразно применить подстановку tgx = t. при этом