1.1.3. Однородные дифференциальные уравнения

Если уравнение или

не меняется при замене x на kx, y на ky, то оно называется однородным.

Однородное дифференциальное уравнение подстановкой

 

 

приводится к уравнению с разделенными переменными.

 Пример. Решить уравнение

Преобразуем уравнение к виду

Так как

, то исходное уравнение однородное.

Полагаем итогда уравнение примет вид

или

Разделив обе части уравнения на  приходим к уравнению с разделенными переменными

Интегрируя его, находим   или

Возвращаясь к старой переменной, получим общий интеграл исходного уравнения в виде

1.1.4. Дифференциальные уравнения, приводящиеся к однородным

Дифференциальное уравнение вида

 

называется приводящимся к однородному. В частности, к этому классу относится уравнение вида

 

(1.10)

Некоторые из коэффициентов (но не одновременно и) могут быть равны нулю.

Следует различать два случая: 

1) Если определитель, то уравнение(1.10)

приводится к однородному подстановкой

(1.11)

где постоянные иопределяются из системы уравнений:

 

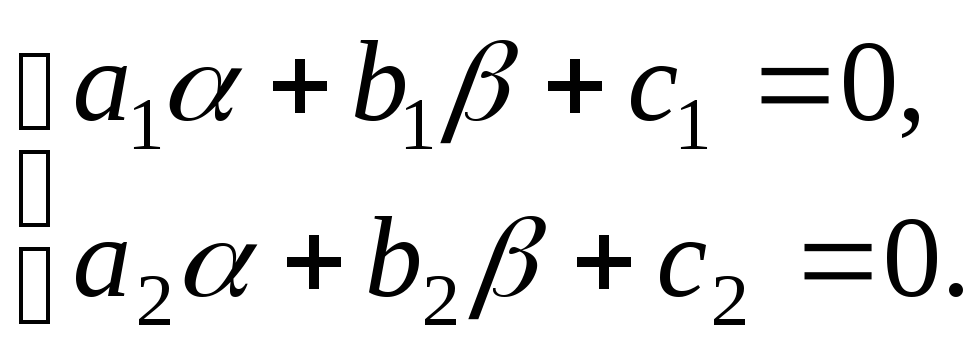
Действительно, учитывая, что следо-

вательно, , и подставляя (1.11) в (1.10), полу-

чим - однородное уравнение относительно

новой функции v(u). Полагая далее t=v/u, приводим последнее уравнение к уравнению с разделяющимися переменными. 

2)Если определитель , то уравнение (1.10)

 

сразу приводится к уравнению с разделенными переменными заменой

 Пример. Решить уравнение

В этом уравнении Поэтому

.   Полагая находими из

системы уравнений:

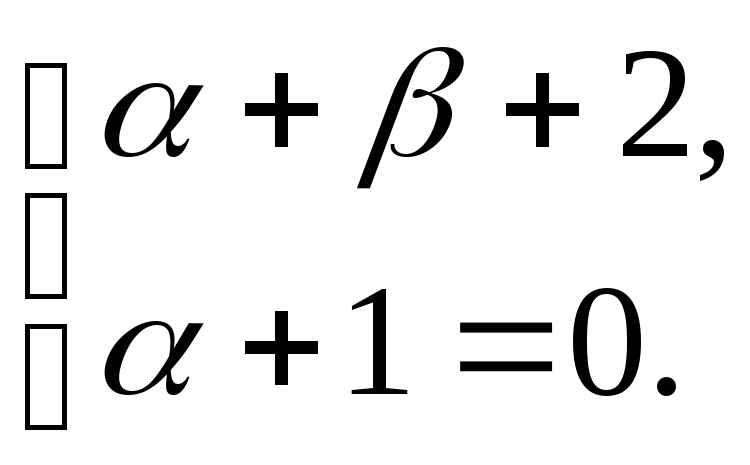следовательно,

Уравнение приводится к однородному  

Полагая далее приходим к уравнению с разделяющимися переменными относительно функции t:

 

 

Возвращаясь к старой переменной, получим

 

 

1.1.5. Линейные дифференциальные уравнения

Линейным дифференциальным уравнением первого порядка называется уравнение вида

(1.12)

содержащее искомую функцию и ее производную в первой степени. Функции P(x) и Q(x) предполагаются непрерывными.

Рассмотрим интегрирование этого уравнения  методом вариации  произвольной постоянной. Сначала ищется решение соответствующего линейного уравнения при нулевой правой части: . Такое уравнение называется линейным однородным. Разделяя в нем переменные, получим его общее решение в виде

 

(1.13)

 

Далее ищется общее решение исходного уравнения с ненулевой правой частью в виде (1.13), но произвольная постоянная в (1.13)заменяется неизвестной функцией

(1.14)

Подставляя (1.14) в (1.12), получаем дифференциальное уравнение с разделяющимися переменными относительно функции v(x), интегрируя которое находим эту функцию. В результате общее решение уравнения (1.12) может быть представлено в виде

(1.15)

Формула (1.15) является общим решением линейного дифференциального уравнения (1.12) в форме Коши.

 Пример. Решить задачу Коши для уравнения при начальном условии y(0)=1. Находим общее решение линейного однородного уравнения. Оно имеет вид

 

Заменяем произвольную постоянную C в этом решении неизвестной функцией v(x):

Вычисляем

 

Подставляя ив исходное уравнение, получим

 

Общее решение уравнения примет вид

 

 

Находим произвольную постоянную C из начального условия: при

x=0 C-1/4=1 C=5/4.

Следовательно, решение задачи Коши будет

 

Решение линейного дифференциального уравнения (1.12) может быть также получено, если искомую функцию представить в виде произведения двух произвольных функций (метод Бернулли [4]):

(1.16)

Тогда (1.17)

Подставляя (1.16) и (1.17) в (1.12), получим

(1.18)

Функцию u(x) подбираем так, чтобы она была одним из решений уравнения

.

После разделения переменных получим

(1.19)

Тогда уравнение (1.18) примет вид

 

.

Следовательно,

Интегрируя это уравнение, находим функцию v:

 

. (1.20)

Подставляя (1.19) и (1.20) и (1.16), получим общее решение уравнения (1.12) в виде (1.15).