4.9 Анализ влияния изменчивости состава бетона на его свойства методом имитационного моделирования.

Имитационное моделирование – это анализ системы по ее математической модели с помощью вариантных расчетов. Реальный эксперимент по изучению системы заменяется машинным экспериментом с математической моделью в режиме имитации процесса функционирования системы на ЭВМ.

Метод имитационного моделирования целесообразен при анализе влияния случайных воздействий на свойства системы, в данном случае, изменчивости состава бетона на его свойства из-за случайных факторов, например, колебаний влажности заполнителей, дозировки компонентов бетонной смеси и других факторов в процессе производства бетонных и железобетонных изделий.

При анализе влияния изменчивости состава бетона на его свойства статистическое имитационное моделирование можно представить в следующем виде (см. рис. 2).

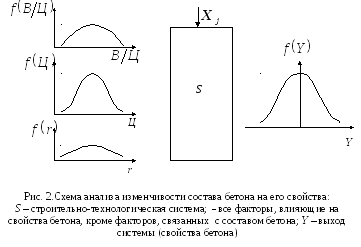
В основе статистического имитационного моделирования лежит универсальный численный метод решения математических задач при моделировании случайных величин – метод Монте-Карло. В этом методе исходные условия в каждом варианте расчета задаются как случайные величины, закон распределения которых известен, а результаты множества реализаций этих вариантов расчета, называемых статистическими испытаниями, рассматриваются как выборочная совокупность значений выхода системы. Для этой совокупности нужно найти статистические оценки неизвестного распределения и сделать инженерные выводи о поведении системы.

При статистическом испытании системы каждый из факторов, характеризующих состав бетона, принимает численное значение в соответствии со своим законом распределения случайной величины, а в результате таких случайных сочетаний будет получена гистограмма распределения выхода системы (свойства бетона). Имитация случайных колебаний анализируемых факторов в соответствии с характерными для данного производства законами распределения этих факторов производится вокруг выбранного рецентурно-технологического решения с помощью имеющегося в ЭВМ генератора чисел.

При анализе влияния изменчивости состава бетона на его свой­ства принимается, что все факторы: В/Ц, Ц и r, или некоторые из них изменяются в процессе производства вокруг проектного уровня по нормальному закону со своими среднеквадратичными от­клонениями , и . Указанные факторы в уравнение (34) подставляются как слу­чайные величины, в общем случае имеющие вид

,

где – проектный уровень фактора (= 0); р – слу­чайные число, распределенное по нормальному закону в диапазоне [0, l] со среднеквадратичным отклонением ; – масштабный коэффициент, который определяет нормализованное факторное пространство случайных колебаний вокруг проектного уровня .

где – среднеквадратичное отклонение каждого фактора в процессе производства; – интервал варьирования факторов при построении математической модели (34).

Если колебания факторов в производственных условиях характеризуется коэффициентами вариации в %, то коэффициент вычисляется по формуле

,

где Х_i – проектный уровень каждого фактора в натуральном виде.

Подставив случайные значения факторов в модель (34) и «проиграв» по ней n вариантов, т.е. произведя n вычислений выхода Y, получают совокупность значений Y, по которой можно построить гистограмму распределения этой величины и рассчитать коэффициент ее вариации.