1 Поставновка задачи

1.1 Общая постановка задачи

Пусть каждый из n объектов a₁, … , a_n характеризуется весом и ценностью. Нужно найти выборку с максимальной суммой ценностей и суммой весов, ограниченной некоторым пределом.

1.2 Цели и задачи курсового проектирования

Целью курсового проектирования является разработка программного продукта, демонстрирующего работу алгоритма поиска оптимального решения с пояснениями.

1.3 Актуальность разработки

Данный программный продукт можно применять в учебных заведениях, где изучают программирование, теорию алгоритмов, а также другие курсы, связанные с поиском оптимального решения.

2 Описание алгоритма оптимального выбора

Решение задачи методом поиска с возвратом сводится к последовательному расширению частичного решения. Если на очередном шаге такое расширение провести не удается, то возвращаются к более короткому частичному решению и продолжают поиск дальше. Данный алгоритм позволяет найти все решения поставленной задачи, если они существуют. Для нахождения оптимального решения из всех, во время формирования решений необходимо оставлять одно, в определённом смысле оптимальное.

В качестве примера общей проблемы поиска оптимального решения

можно выбрать такую задачу: руководствуясь некоторыми ограничениями, найти оптимальную выборку из заданного множества объектов. Выборки, представляющие приемлемые решения, строятся постепенно: один за другим просматриваются отдельные объекты из исходного множества. При рассмотрении каждого возможны два варианта – включать исследуемый объект в текущую выборку или не включать.

Соответственно, существует всего 2ⁿ возможных выборок, где n – количество объектов. В зависимости от критерия оптимальности, количество возможных выборок может меняться. Значит, необходимо использовать такой критерий, который значительно сокращает число перебираемых кандидатов.

На примере вышеописанной проблемы поиска оптимального решения, предположим, что каждый из имеющихся объектов характеризуется весом и ценностью. Оптимальной назовём выборку с максимальной суммой ценностей и суммой весов, не превышающей некоторый предел. Тогда следует определить критерий приемлемости объекта для текущей выборки. Если речь идёт о включении, то объект можно включать в выборку, если он подходит по весовым ограничениям. Иначе попытки добавить ещё один объект в текущую выборку можно прекратить. Но, если речь идёт об исключении, то критерием приемлемости будет то, что после данного исключения общая ценность будет не меньше полученной до этого момента оптимальной выборки. Это основано на том, что, если общая ценность после исключения меньше оптимума, то продолжение поиска не приведёт к оптимальному решению.

Такая реализация алгоритма с возвратом, использующая некоторые ограничения для уменьшения роста потенциального дерева поиска, называется алгоритмом ветвей и границ.

3 Выбор метода решения

Для поиска оптимального решения был выбран модифицированный алгоритм с возвратом – метод ветвей и границ. Согласно данному методу, поиск решения будет строиться постепенно, учитывая определённые ограничения оптимальности. На основе критерия оптимальности, из множества решений будет выбираться оптимальное – путём сравнения текущего решения с оптимальным решением, полученным на данный момент.

Предположим, что существует множество объектов с характеристиками веса и ценности. Определим эти характеристики переменными: вес – ob.Weight, ценность – ob.Price. Множество этих объектов хранится в векторе Objects. Так же имеются две функции обработки объектов. Одна добавляет объект в текущую выборку – Add(i), другая удаляет объект из текущей выборки – Del(i), где i – индекс объекта, над которым производится действие. Тогда, при наличии переменных хранения значений оптимальной ценности – optPrice и ограничения веса – WeightMax, можно описать функцию Optimal(i, curWeight, MaxPrice), которая непосредственно выполняет поиск оптимального решения. В качестве параметров функция Optimal принимает значение индекса(i), вес текущей выборки(curWeight) и общий вес всех объектов из вектора Objects(MaxPrice). Для упрощения блок-схемы добавим функцию Solution(), которая не принимает параметры, а просто каким-то образом переопределяет текущую выборку оптимальной.

Учитывая всё это, входными данными для данного алгоритма являются объекты с их характеристиками и ограничение веса. Блок-схема алгоритма поиска оптимального решения изображена на рисунке 3.1.

Р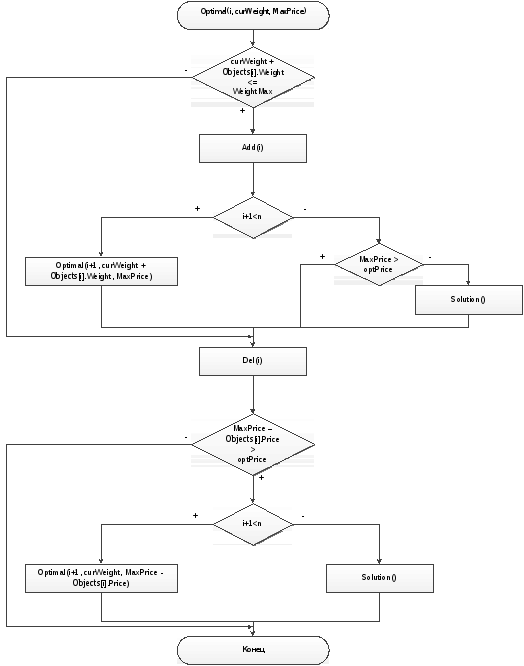исунок 3.1 – Блок-схема алгоритма поиска оптимального решения