ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ МОСКОВСКОЙ ОБЛАСТИ
«Международный университет природы, общества и человека «Дубна»
Кафедра высшей математики
КУРСОВАЯ РАБОТА
по «Теории вероятностей и математической статистике»
на тему:
Исследование корреляционной зависимости по выборке
|
|
Выполнил: студент 2072 группы 2 курса ИСАУ Иванов Максим Сергеевич ________________________________ Руководители: к. ф.-м. н., доц. С. В. Панферов Дата защиты: ________________________________ Оценка: ________________________________
________________________________
|
Содержание
Введение 3
Постановка задачи 4
Теоретическая часть 5
Случайные величины 5
Система двух случайных величин 6
Практическая часть 8
Заключение 14
Список используемой литературы 15
Введение
Данная курсовая работа посвящена исследованию характера зависимости между приростом населения и смертностью. Цель данной работы заключается в рассмотрении и изучении взаимосвязи двух наборов статистических данных о приросте населения и смертности в России.
Объектом исследования являются понятия прироста населения и смертности. Предметом исследования является их взаимосвязь.
В этой работе будет изучена зависимость прироста населения от уровня смертности с 1992 по 2011 год.
Постановка задачи
Математической
статистикой называется наука, занимающаяся
методами обработки опытных данных,
полученных в результате наблюдений над
случайными явлениями. Любой такой
результат можно представить как
совокупность значений, принятых в
результате
опытов какой-то случайной величиной
или системой случайных величин.
В
нашем случае данные — это выборка, в
которой
величина
— это
уровень смертности по стране в процентах
в фиксированный промежуток времени
(год),
—
уровень прироста населения по стране
(в год), также в процентах. Объем выборки
— 20 значений по
и
по
.
При этом следует помнить, что данные из этой выборки фиктивны, то есть не отражают реального положения дел в демографии страны. В этой работе важен сам механизм исследования и обработки исходных данных, а не результат этих исследований.
Наша задача, используя данный статистический материал, упорядочить его, представить в наиболее удобном для обозрения и анализа виде, проанализировать при помощи различных графиков и таблиц.
Теоретическая часть Случайные величины
Случайная величина — это величина, которая принимает в результате опыта одно из множества значений, причем появление того или иного значения этой величины до ее измерения нельзя точно предсказать.
Дискретной (прерывной) называют случайную величину, которая принимает отдельные, изолированные возможные значения с определенными вероятностями. Число возможных значений дискретной случайной величины может быть конечным или бесконечным.
Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности.
Пусть
случайная величина
может принимать только значения
,
вероятности которых соответственно
равны
.
Тогда математическое ожидание
M()
случайной величины определяется
равенством:
.
Если дискретная случайная величина принимает счетное множество возможных значений, то
Для вычисления дисперсии часто бывает удобно пользоваться следующей формулой:
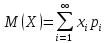. (1)
Пусть
—
случайная величина и
—
ее математическое ожидание.
Отклонением
называют разность между случайной
величиной и ее математическим ожиданием
.
Дисперсией (рассеянием) дискретной случайной величины называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания.
.
Для вычисления дисперсии часто бывает удобно пользоваться следующей формулой:
. (2)
Для оценки рассеяния возможных значений случайной величины вокруг ее среднего значения кроме дисперсии служат и некоторые другие характеристики. К их числу относится среднеквадратическое отклонение.
Среднеквадратическим отклонением случайной величины называют квадратный корень из дисперсии:
.