7.5.Характеристическое уравнение

Характеристическое уравнение составляется по системе дифференциальных уравнений, которая записывается на основе законов Кирхгофа.

Вещественная часть корней будет положительной, если R<0. В общем случае такое может быть, если цепь нелинейная.

Если цепь передает электрический сигнал, то она характеризуется коэффициентом передачи .

Характеристическое уравнение есть знаменатель коэффициента передачи.

Например: .

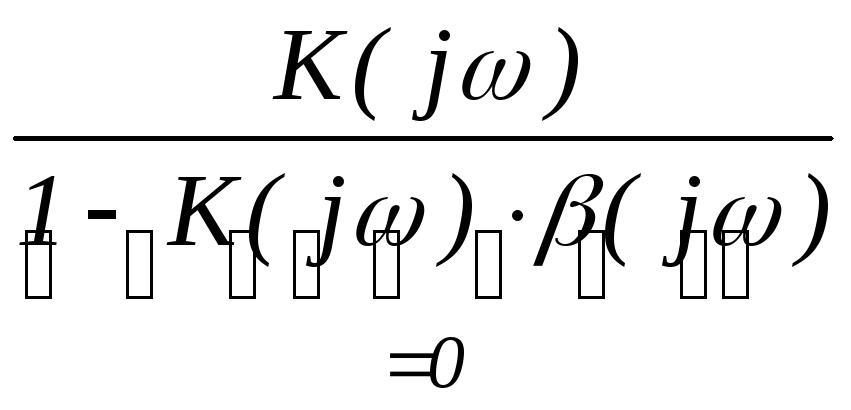Если цепь сложная, то уравнение получается высокого порядка и корни искать трудно. Для того чтобы не вычислять корни, были разработаны критерии устойчивости.

7.6.Критерии устойчивости

1. Критерий Рауса-Гурвица

Полиномы некоторой переменной p называются полиномами Гурвица, если у них все коэффициенты вещественные, а все корни находятся в левой полуплоскости (отрицательная вещественная часть).

Вычисляется определитель их коэффициентов полинома, состоящий из m столбцов и m строк:

Для устойчивой цепи . Кроме того, вычисляются миноры. Все главные миноры должны быть положительными.

2. Критерий Михайлова

Здесь рассматривается характеристический полином в комплексной форме.

K-ый корень можно записать:. Тогда

Получим:

Частоту меняют от 0 до бесконечности и смотрят, что происходит с углом.

Цепь будет устойчива, если .

Строят годограф вектора характеристического уравнения.

3. Критерий Найквиста

Он используется для цепей с явной обратной связью.

Когда , цепь неустойчива. Произведение называют петлевым усилением.

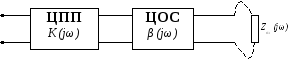
Получаем, что цепь устойчива, когда петлевое усиление не превышает единицы.

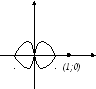
Опять используют годограф. На рисунке показан пример годографа устойчивой цепи. Для устойчивой цепи годограф не должен охватывать точку с координатами (1;0).

7.7. Автоколебательные цепи или автогенераторы

Автогенераторы – это такие устройства, которые без внешнего гармонического воздействия вырабатывают колебания какой-то формы (в частности, гармонической). В принципе в них должны быть источники питания (постоянного напряжения или тока), нелинейные элементы и положительная обратная связь (в явной или неявной форме).

Рассмотрим структуру автоколебательной цепи с явной обратной связью.

Рассмотрим петлевое усиление. Если на какой-то частоте, то автогенератор будет вырабатывать гармонические колебания.

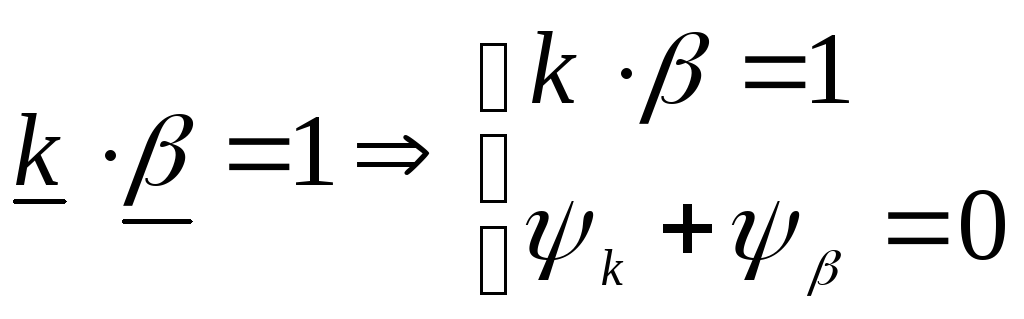- это баланс амплитуд и фаз

Сам усилитель и обратная связь должны быть по отдельности устойчивы, а вместе – неустойчивы.

Для того, чтобы было возбуждение, необходимо, чтобы немного превышало 1.

В простейшем случае усилитель – это ИНУН, в котором коэффициент управления превышает единицу, т.е. это частично независимая цепь.

Цепь обратной связи (ЦОС) – частотно-зависимая цепь (содержит индуктивность, емкость).

По типу элементов разделяют RC-автогенераторы, LC-автогенераторы, транзисторные автогенераторы, на операционных усилителях. Могут быть генераторы на специальных диодах (туннельных), но это генераторы с внутренней обратной связью.

7.8. RC-автогенераторы

Рассмотрим RC-автогенератор на операционном усилителе.

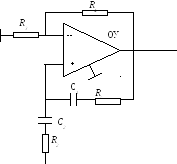
Вход с минуса называется инвертирующим (здесь фаза изменяется на 180⁰).

У идеального ОУ входное напряжение бесконечно велико, а выходное равно 0. Схема замещения идеального ОУ выглядит следующим образом:

Рассмотрим транзисторный RC-автогенератор.

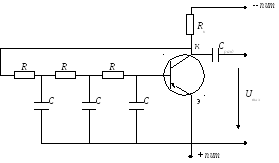
Сдвиг фаз .

Для получения такого сдвига фаз необходимы 3 RC-цепочки. Тройная RC-цепочка ослабит входное напряжение примерно в 27 раз. Для точных расчетов надо составить схему замещения такой цепи с учетом схемы замещения транзистора в соответствующем диапазоне частот. Обратная RC-цепочка дает сдвиг фаз .

7.9. LC-автогенераторы

В них используется колебательный контур и обратная связь через трансформатор или взаимную индуктивность.

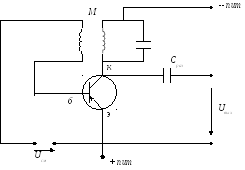
Напряжение смещения выбирают таким образом, чтобы установить точку транзистора в середине линейного участка. Схема замещения контура с учетом влияния обратной связи:

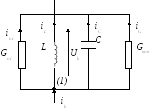
Здесь: G_oc – проводимость обратной связи, G_кон – проводимость контура, i_k – коллекторный ток.

Составим уравнение по первому закону Кирхгофа для узла (1):

Составим характеристическое уравнение:

Мы можем сделать вывод, что . График зависимости i_k(U_бэ) характеризуется величиной крутизны S.

, , где – резонансное сопротивление параллельного контура.

Определим М_крит:

Частота генератора равна частоте колебаний контура.

7.10. LC-автогенераторы с внутренней обратной связью

Используется специальный диод, например, туннельный, и колебательный контур.

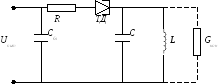
У туннельного диода специфическая ВАХ:

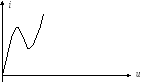
Туннельный диод можно характеризовать некоторой отрицательной дифференциальной проводимостью.

Схема замещения похожа на схему замещения транзисторного LC-автогенератора.

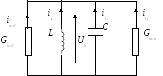
Условие колебаний: .

Проводимость туннельного диода должна компенсировать потери в контуре.

Дисциплина «Основы теории цепей (часть II)»; преподаватель Михайлов В.И.