Закон Фарадея для самоиндукции

При постоянной индуктивности можно записать

ЭДС самоиндукции прямо пропорциональна индуктивности катушки и скорости изменения силы тока в ней.

В случае, когда скорость изменения силы тока не постоянна, ЭДС самоиндукции следует вычислять как производную собственного магнитного потока, взятую с обратным знаком.

Из закона Фарадея для самоиндукции следует связь между единицами измерения магнитных и электрических величин

Энергия магнитного поля

Магнитное поле обладает энергией. Подобно тому, как в заряженном конденсаторе имеется запас электрической энергии, в катушке, по виткам которой протекает ток, имеется запас магнитной энергии.

Энергия магнитного поля вычисляется как половина произведения индуктивности контура на квадрат силы тока в нем:

W=LI²/2

Отсюда для единиц измерения

Дж = Гн *А² ; Дж=В* Кл

Домашнее задание (повышенная сложность): Доказать, что индуктивность соленоида пропорциональна квадрату числа витков.

Переменный ток Лекция 5 Введение. Немного математики

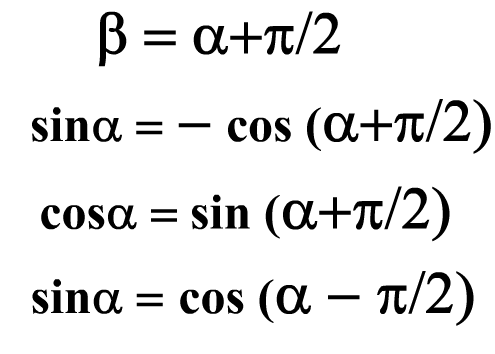
радианная мера угла

Производные

Тригонометрической функции: (cosx)^/ = - sinx (sin x)^/ = + cosx

Показательной функции (xⁿ)^/ = nx^n-1

Независимая переменная не координата х, а время t

x ==>t f(x)==> f(t)

Производная сложной функции равна произведению производной функции на производную аргумента

(cosωx)^/ = - ωsinωx (Acosωx)^/ = - Aωsinωx

(sinωx)^/ = ωcosωx (Asinωx)^/ = ωAcosωx

Гармоническая функция

Гармонической называется функция, которая изменяется по закону синуса или косинуса:

x = Acos(ωt+α₀) x = Asin(ωt+α₀)

A – амплитуда – максимальное отклонение изменяющейся величины от положения равновесия

(ωt+α₀) – фаза α

α₀ – начальная фаза – значение фазы в момент времени =0

ω – циклическая частота или угловая скорость

ν=ω/2π - частота- число колебаний в единицу времени

Т – период Т=1/ν = 2π/ ω – время одного полного колебания

Фаза α и период Т связаны соотношением: α =(ωt+α₀) = (2πt/Т+ α₀)

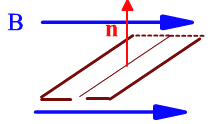
Вращение рамки в однородном магнитном поле

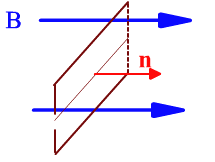
Поместим рамку в однородное магнитное поле

перпендикулярно силовым линиям и начнем

вращать ее с постоянной угловой скоростью ω.

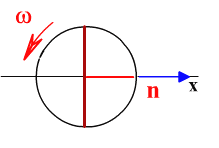
В начальный момент времени

нормаль к плоскости рамки параллельна

силовым линиям. Начальная фаза α = α₀ =0.

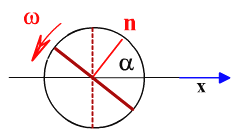
Через время t рамка повернется на угол α.

На рисунке α - угол между вектором магнитной

индукции и силовыми линиями, изменяется

со временем по закону α=ω t.

Магнитный поток через рамку

Ф=BS cosα

α=ω t

Ф=BS cos ω t или Ф= Ф₀ cos ω t, где Ф₀ = BS – амплитуда магнитного потока.

Поскольку магнитный поток через рамку изменяется со временем, в ней появляется ЭДС индукции. Ее значение определяем по закону электромагнитной индукции как производную от магнитного потока, взятую с обратным знаком:

e_i = - Ф^/

e_i =BS ω sin ω t

e_i =e₀ sin ω t , где e_{0 =} BSω – амплитуда ЭДС индукции

Магнитный поток и ЭДС индукции изменяются по гармоническому закону.

В начальный момент времени (t=0) магнитный поток максимален, ЭДС индукции равна нулю. В рассмотренном примере начальная фаза α₀ =0. Получен результат:

Ф=BS cos ω t Ф₀ = BS

e_i =e₀ sin ω t e_{0 =} BS ω

в начальный момент времени ( t=0): Ф = Ф₀ e_i =0

Возможно любое другое начальное положение рамки. Например, такое:

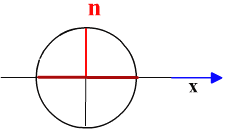
t=0

начальная фаза α₀ =π/2

П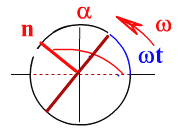оложение рамки через время t

угол между нормалью к плоскости рамки и

силовыми линиями (фаза) равен α=ω t + π/2

Магнитный поток

Ф=BS cos (ω t + π/2 ) = -Ф₀ sin(ω t), Ф₀ = BS

ЭДС индукции e_i =-(-BS ω cos ω t) =e₀ cos ω t , e_{0 =} BS ω

В начальный момент времени (t=0) магнитный поток равен нулю, ЭДС индукции максимальна: Ф=0, e_i = e_0.