Выводы по второму разделу

В этом разделе был синтезирован методом желаемых ЛАЧХ и собран на операционных усилителях регулятор тока, благодаря которому контур тока удовлетворяет требованиям критериальной стратегии синтеза. Кроме того, регулятор обеспечивает контуру тока астатизм первого порядка.

3 Синтез регулятора скорости

В этом разделе будет синтезирован регулятор скорости. Синтез будет проведен двумя различными методами: методом двупараметрического RD-разбиения и методом АФИ-коррекции. Оба регулятора обеспечат контуру скорости астатизм 2-го порядка. После синтеза регулятора скорости двумя методами, будет сделан вывод, какой из регуляторов обеспечивает лучшие характеристики контуру скорости и соответственно какой из методов предпочтительнее использовать.

3.1 Синтез регулятора скорости методом двупараметрического расширенного d-разбиения

Выделим в схеме привода (рисунок 1) объект управления, регулятор которым будем синтезировать, и найдем его ПФ. Для этого преобразуем схему на рисунке 1 к следующему виду

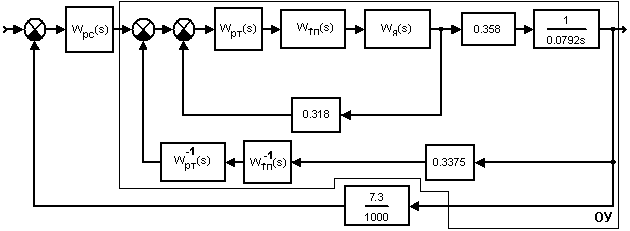
Рисунок 18 — Преобразованная структурная схема контура скорости

Выпишем ПФ ОУ в контуре скорости (рисунок 18) с учетом синтезированного регулятора тока и без учета входа возмущения в канонической форме.

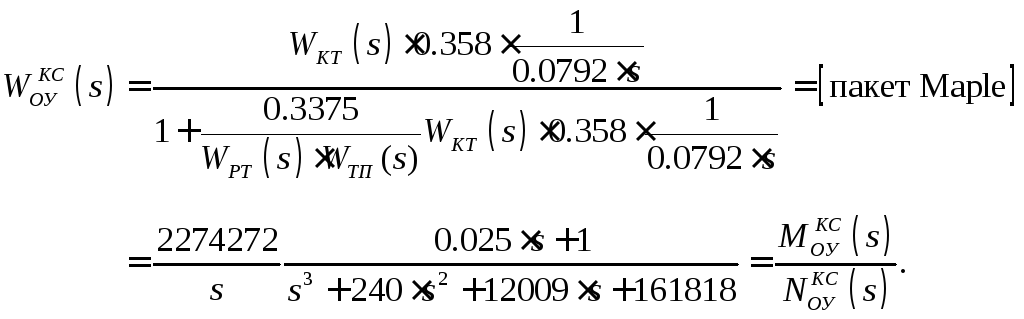(10)

При синтезе этим методом сначала выбирается вид регулятора. Собственно метод двупараметрического RD-разбиения служит для нахождения значений параметров регулятора выбранного типа в соответствии с требованиями критериальной стратегии.

Синтезировать будем параметры ПИ-регулятора с несвязными настройками

. (11)

Как обычно перед синтезом регулятора задаемся критериальной стратегией синтеза: быстродействие t= 3.33 сек; колебательность ψ_КС= 0.9.

Запишем ПФ замкнутого контура скорости с ПИ-регулятором

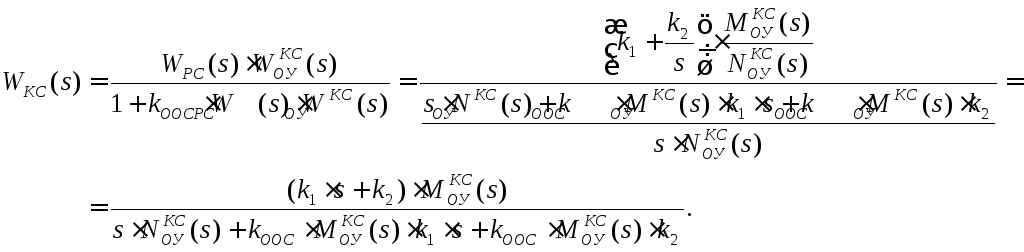(12)

Таким образом, характеристический полином замкнутого контура скорости:

. (13)

В зависимости от параметров k₁ и k₂ХП будет иметь различные корни, а контур скорости соответственно различные свойства. Подставив в выражение для ХП комплексное расширение

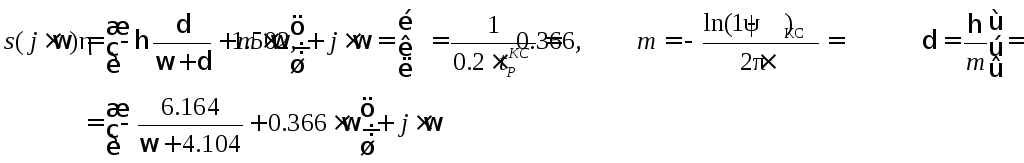,(14)

можно получить выражения, на основе которых строятся области, в которых k₁ и k₂принимает нужные нам значения. Соответствующая методика описана в курсе ТАУ [2]. Вручную получить такие выражения очень сложно, поэтому воспользуемся математическим пакетом Maple, составив в нем программу расчета (текст программы приведен в ПриложенииB).

В результате работы программы получим:

— главный определитель:

— определитель для k₁:

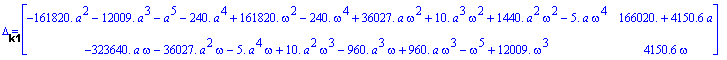
— определитель для k₂:

()

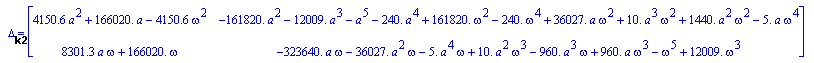
Тогда . Уравнение особой прямой (получается при= 0):.

Строим годограф RD-разбиения (рисунок 19). Чтобы выполнить правильно штриховку годографа, возьмем 7 точек (k₁, k₂) из различных областей на рисунке 19, и, подставив их в (13), найдем корни ХП замкнутого контура скорости.

Получим условие того, что корни ХП принадлежат области качества. Кривая, ограничивающая область качества (14), может записана в следующем виде, сопоставив координате х вещественную часть, а координате y — мнимую:

. (15)

Качественные корни — это корни, лежащие левее кривой (15). Значит, для того чтобы корень p_iбыл качественным, он должен удовлетворять неравенству

. (16)

Проверка этого условия была заложена в упомянутую выше программу. В результате было выяснено, сколько в различных областях рисунка 19 некачественных корней. Из курса ТАУ [2] известно, что при переходе из области двойной штриховки в область без штриховки теряются 2 качественных корня, а при переходе из области одинарной штриховки — 1 качественный корень. С учетом этого была произведена штриховка годографа RD-разбиения (рисунок 19) и тем самым было точно установлено, что область (a ‑ b ‑ c) — искомая область качества: k₁[32, 78],k₂[28, 135].

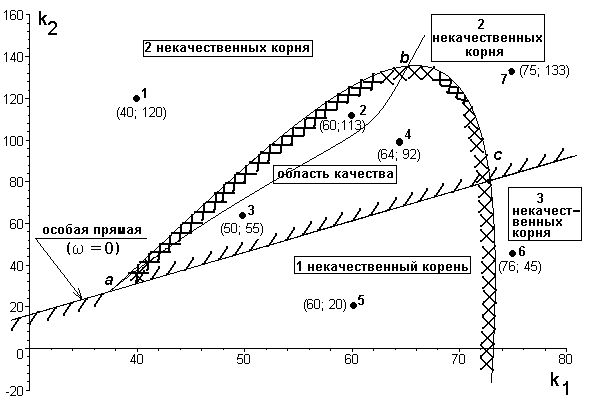
Рисунок 19 — Годограф двупараметрического RD-разбиения

Для наглядности приведем переходные процессы замкнутого контура скорости для 7 пар значений параметров настройки ПИ-регулятора (номера точек по порядку показаны на рисунке 19) при номинальном значении входного напряжения в 7.3 В (рисунки 19-25).

Рисунок 19 — Переходный процесс при k₁=40,k₂= 120(a ‑ b ‑ c) - точка 1

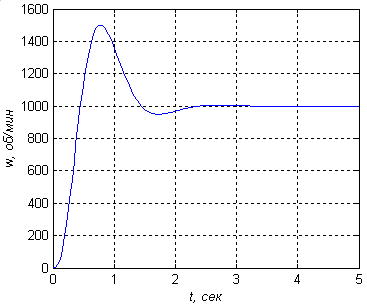
Рисунок 20 — Переходный процесс при k₁=60,k₂= 113(a ‑ b ‑ c) - точка 2

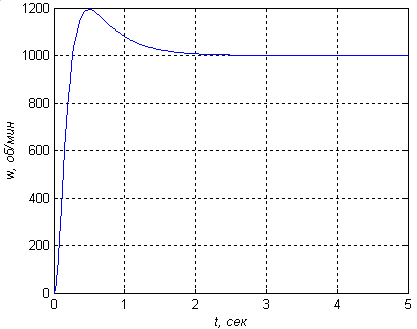
Рисунок 21 — Переходный процесс при k₁=50,k₂= 55(a ‑ b ‑ c) - точка 3

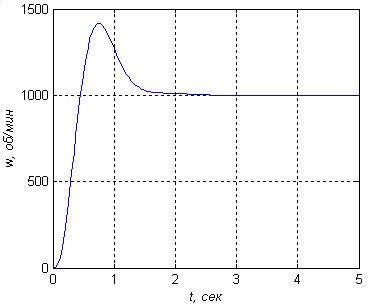
Рисунок 22 — Переходный процесс при k₁=64,k₂= 92(a ‑ b ‑ c) - точка 4

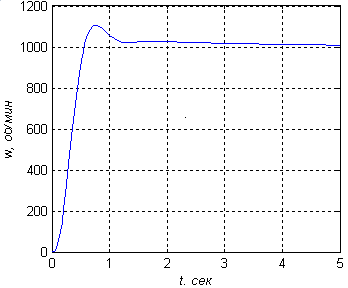
Рисунок 23 — Переходный процесс при k₁=60,k₂= 20(a ‑ b ‑ c) - точка 5

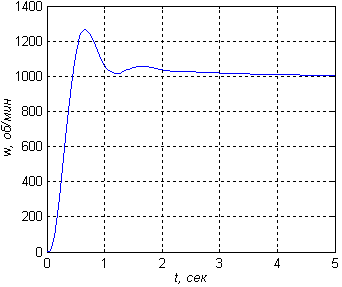
Рисунок 24 — Переходный процесс при k₁=76,k₂= 45(a ‑ b ‑ c) - точка 6

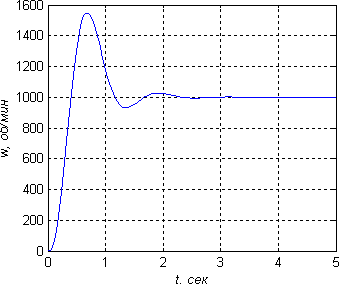
Рисунок 25 — Переходный процесс при k₁=75,k₂= 133(a ‑ b ‑ c) - точка 7

Для окончательного решения задачи синтеза выберем в области (a - b - c) значения параметров настройки в качестве окончательного варианта. Выбор произведем с учетом инженерных запасов по модулю и фазе системы с ПИ-регулятором.

Структурная схема разомкнутого контура скорости (РКС) в свернутом виде приведена на рисунке 26.

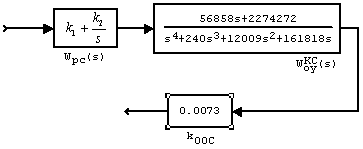
Рисунок 26 — Структурная схема разомкнутого контура скорости

Выпишем ПФ разомкнутого контура скорости

. (13)

Как видно из (13) порядок разомкнутого контура равен 5 при первом порядке астатизма, значит, согласно таблицам (см.[1]) инженерные запасы устойчивости по модулю должны быть 20 дБ L25 дБ, а по фазе — 70120.

Набираем схему разомкнутого контура скорости (рисунок 26) в пакете CLASSIC. Из рисунков 20-22 видно, что наиболее качественный ПП замкнутый контур скорости имеет при значениях параметров настройки в районе k₁= 50,k₂= 55. Построим для этих значений ЛАЧХ и ЛФЧХ разомкнутого контура.

Как следует из рисунка 15, запасы устойчивости = 80, аL = 36 дБ, значит, замкнутый контур скорости с ПИ-регулятором, имеющим параметрыk₁= 50,k₂= 55, удовлетворяет инженерным запасам устойчивости. Итак, регулятор скорости

. (14)

Переходный процесс контура скорости с синтезированным регулятором изображен на рисунке 21.

Рисунок 27 — ЛАЧХ и ЛФЧХ разомкнутого контура скорости при k₁= 50,k₂= 55