2.7 Критерий Найквиста

Для устойчивости замкнутой системы, при устойчивой разомкнутой системе, необходимо и достаточно, чтобы годограф Найквиста, построенный для разомкнутой системы, не охватывал точку .

Проверим на устойчивость разомкнутую систему по критерию Гурвица. Характеристическое уравнение для этой системы имеет следующий вид:

Составим определитель Гурвица:

>0

>0

>0

Все коэффициенты характеристического уравнения и диагональные миноры определителя Гурвица положительны, следовательно, разомкнутая система устойчива.

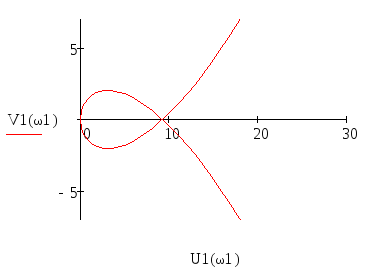
Построим годограф Найквиста для разомкнутой системы, воспользовавшись программой Matlab 7.0.1. Получаем следующий график:

Рисунок 3- Годограф Найквиста для разомкнутой системы

Годограф Найквиста для разомкнутой системы не охватывает точку . Следовательно, замкнутая система устойчива.

2.8 Определение области устойчивости с помощью D-разбиения по одному параметру.

Характеристическое уравнение системы имеет вид:

Для заданного характеристического уравнения построим область устойчивости по параметру a₃=3.

Произведем замену p=jω и приравняем правую часть к нулю.

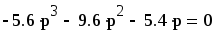
Выделим действительную и мнимую части и построим график:

2

3

k-1

k-2

1

k

Рисунок 4-D-разбиение

Определим область наибольшей устойчивости:

k+i=n,

где k-количество отрицательных корней уравнения,

n- порядок характеристического уравнения,

1. область наибольшей устойчивости.

Определим корни уравнения:

k=2

Тогда i = n-k=3-2=1. Получили, что областью наибольшей устойчивости является область 1. Коэффициент a₃=3 также принадлежит этой области.

Вывод: в ходе лабораторной работы я изучила методы исследования устойчивости стационарных и нестационарных линейных непрерывных и дискретно непрерывных САР.