Лабораторные работы / 2и3

БАЛАКОВСКИЙ ИНСТИТУТ ТЕХНИКИ, ТЕХНОЛОГИИ И УПРАВЛЕНИЯ

ФАКУЛЬТЕТ ИНЖЕНЕРНО-СТРОИТЕЛЬНЫЙ

КАФЕДРА УПРАВЛЕНИЕ И ИНФОРМАТИКА В ТЕХНИЧЕСКИХ СИСТЕМАХ

ПРАКТИЧЕСКАЯ РАБОТА №2,3

по дисциплине

Локальные системы управления

Выполнил ст. гр. УИТ-51

Удалов Ю.В.

Принял

Ефремова Т.А.__________

«____» _____________2004г.

2004

Вариант 23

Передаточная функция непрерывной части системы (разомкнутой цепи) Wraz(s): Wraz=tf([0.008323],[0.01 0.4 1 0])

Transfer function:

0.008323

----------------------

0.01 s^3 + 0.4 s^2 + s

Передаточная функция замкнутой системы Wzam(s)

Wzam=Wraz/(1+Wraz)

Transfer function:

0.1224 s^3 + 4.896 s^2 + 12.24 s

--------------------------------------------------------

0.0001 s^6 + 0.008 s^5 + 0.18 s^4 + 0.8001 s^3

+ 1.003 s^2 + 0.008323 s

Перейдем от непрерывной модели объекта к дискретной с интервалом дискретизации 0.01 c, используя экстраполятор нулевого порядка, для этого воспользуемся в программе MATLAB функцией преобразования непрерывной модели системы в дискретную (с2d).

Ts=0.01;Wdis(z)=c2d(Wraz,Ts,'zoh') , получим передаточную функцию разомкнутой дискретной системы:

Ts=0.01;Wdis=zpk(c2d(Wraz,Ts,'zoh'))

Zero/pole/gain:

1.2582e-007 (z+3.387) (z+0.2418)

--------------------------------

(z-1) (z-0.9736) (z-0.6885)

Sampling time: 0.01

Для проверки качества выполненной аппроксимации сравним частотные характеристики исходной непрерывной и полученной дискретной моделей, изображенные на рисунке. ЛАЧХ дискретной модели строится в зависимости от псевдочастоты λ, при этом сначала проводится ω-преобразование заменяя z=(1+ω)/(1-ω), а затем осуществляется переход от W(ω) к частотному выражению передаточной функции через псевдочастоту λ путем замены ω=0.5Tsλj.

Из рисунка следует, что аппроксимация выполнена верно.

Построим АЧХ разомкнутой системы

Построим желаемую ЛАЧХ методом запретной зоны.

Зададим скорость обработки сигнала:

g1=25

g1 =

25

Ускорение:

g11=100

g11 =

100

Максимальная ошибка регулирования:

e=0.15

e =

0.1500

Построение ЖЛАЧХ начинаем с построения запретной зоны, геометрия которой определяется положением рабочей точки РТ.

частота рабочей точки (hm)

hm=g11/g1

hm = 4 рад/с

hml=Log10(hm)

амплитуда рабочей точки A

Amax=0.00787

Amax =

0.0079

A=Amax/e

A =

0.0525

Al=20*log10(A)

Al =

-25.6023 дБ

Т.о., РТ(4; -25.6) – координаты рабочей точки.

Через найденную точку проводим прямую под наклоном -20 дБ/дек - асимптоту рабочей точки. Область, ограниченная координатными осями и полученной прямой, является запретной зоной.

Зададим время регулирование t_p=10 c и величину перерегулирования σ=30%,колебательности (М=1.3), тогда, согласно номограмме Солодовникова, Р_мах составит 1.27, а частоту среза найдем из формулы:

Таким образом, ω_ср=1.1 рад/с.

Тогда(hsr)

hsr=1/(0.01*0.5)

hsr =

200

hsrl=log10(hsr)

hsrl =

2.3010

Определим графически краевую частоту, расположенную правее - она является точкой пересечения асимптоты рабочей точки и горизонтальной прямой

M=1.4

M =

1.4000

hkr2=20*log10(M/(M+1))

hkr2 =

-4.6817

hkr1=20*log10(M/(M-1))

hkr1 =

10.8814

Правее ЖЛАЧХ идёт с наклоном параллельно построенной ранее ЛАЧХ.

0.52*1.04+20.22

ans =

20.7608

Построение запретной зоны

Таким образом, желаемая передаточная функция разомкнутой системы будет:

GW=zpk([-57.7 -57.7],[0 -2.679 -37.32 -344 -344],[30000000])

Zero/pole/gain:

30000000 (jh+57.7)^2

-------------------------------

jh (jh+2.679) (jh+37.32) (jh+344)^2

желаемая передаточная функция замкнутой системы

GWZ=GW/(1+GW)

Transfer function:

3e007 jh ^7 + 2.53e010 jh ^6 + 6.999e012 jh ^5 + 7.221e014 jh ^4 + 3.156e016 jh ^3

+ 5.206e017 jh ^2 + 1.182e018 jh

----------------------------------------------------------------------------------

jh ^10 + 1456 jh ^9 + 8.219e005 jh ^8 + 2.521e008 jh ^7 + 5.362e010 jh ^6 + 8.418e012 jh ^5

+ 7.486e014 jh ^4 + 3.167e016 jh ^3 + 5.207e017 jh ^2 + 1.182e018 jh

Переходный процесс в замкнутой системе

до после

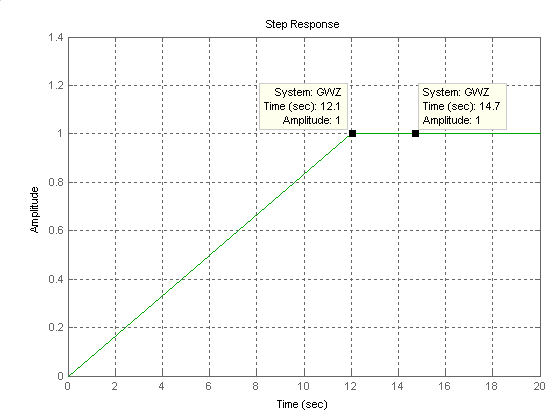
1.4872 (z+1.198) (z+0.03958) (z^2 - 1.125z + 0.3163)

-----------------------------------------------------

(z-1) (z-0.9736) (z-0.6885) (z-0.03206)^2

1.2582e-007 (z+3.387) (z+0.2418)

--------------------------------

(z-1) (z-0.9736) (z-0.6885)

Передаточную функцию последовательного корректирующего устройства определим по формуле:

Wk=GW/Wraz

Zero/pole/gain:

36044695.4223 (s+57.7)^2

----------------------------------

(s+344)^2

ЛАЧХ последовательного корректирующего устройства

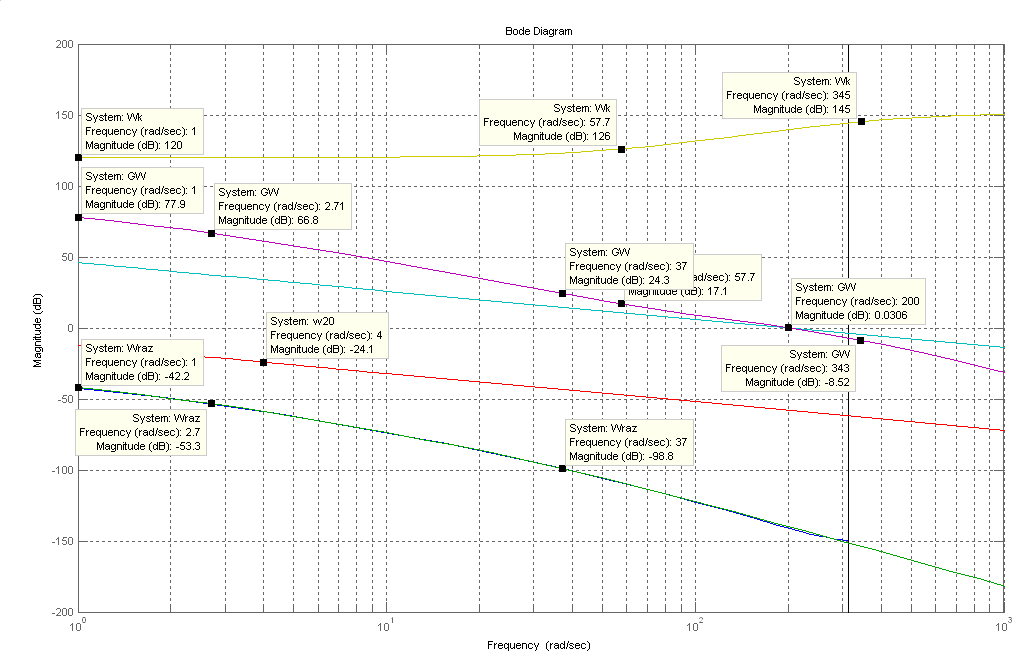
Найдем передаточную функцию соответствующего параллельного корректирующего устройства:

Wpark=Wraz*(Wk-1)

Zero/pole/gain:

29999999.1677 (s+57.75) (s+57.65)

-----------------------------------------------

s (s+37.32) (s+344)^2 (s+2.679)

Найдем передаточную функцию соответствующего встречно-параллельного корректирующего устройства:

Wvpark=(1-Wk)/(Wraz*Wk)

Zero/pole/gain:

-1.2015 s (s+57.65) (s+37.32) (s+344)^2 (s+2.679)

-----------------------------------------------------------------

(s+344)^2 (s+57.7)

Для реализации выбираем последовательное корректирующее устройство, так как его наиболее просто реализовать

Wk=GW/Wraz

Zero/pole/gain:

36044695.4223 (0.0173*s+1)^2

----------------------------------

(0.0029*s+1)^2

При таком виде ЛАЧХ КУ по справочнику находим вид КУ. Получаем, что при таком виде ЛАЧХ корректирующего устройства, желаемую передаточную функцию корректирующего звена можно реализовать двумя одинаковыми дифференцирующими четырехполюсниками с разделительным усилителем изобразим его схему на рисунке.

Схема корректирующего устройства

Передаточная функция дифференцирующего четырехполюсника:

,

где T₁=R₁∙C₁= 0.0173;

T₂=K_K1∙T₁=0.0029.

K_K1=R₂/(R₁+R₂)=0.16;

При этом усилитель должен иметь коэффициент усиления: