
Лекции / Лекции по дисциплине ЛСУ
.pdf
Подбирается:
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|||
|
|
|
|
|
|
2 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
m |
|
|
|
|
|
F Asin |
|
|
|
|
a A, n, sin |
|
|
b A, n, cos |
|
|
t dt |
(5) |
|||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
nT |
|
|
nT |
|
|
|
|
|
|
|
nT |
|
nT |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
0 0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
0 |
|
|
0 |
|
|
|
|||||||
|
|
|
m |
|
2 – наибольшее квадратическое приближение |
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
n 1 |
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a A, n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
F Asin |
|
|
|
sin |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
An k 0 |
|
nT0 |
|
|
|
|
|
n |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
n 1 |
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b A, n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
F Asin |
|
|
|
cos |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
An k 0 |
|
nT0 |
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|||
J A, n, q A, n, e j |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|||
q A, n, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
a2 A, n, b2 A, n, |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
k |
|
|
|
|
|
|
b A, n, |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
arctg |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
a A, n, |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Вопросы самоконтроля:
1.Перечислите порядок проведения статической линеаризации существенных нелинейных элементов.
2.Перечислите порядок проведения совместной гармонической и статической линеаризации нелинейных элементов.
3.Назовите понятие существенных дискретных нелинейных элементов.
ЛЕКЦИЯ №8 Цель лекции: Изучить порядок составления структурных схем ЛСУ в вектор-
но-матричной форме, понятия управляемости и наблюдаемости.
Задачи лекции:
1.Порядок составления структурных схем ЛСУ в векторно-матричной форме.
2.Понятия управляемости и наблюдаемости.
Желаемый результат:
Студенты должны знать:
1.Порядок составления структурных схем ЛСУ в векторно-матричной форме.
2.Понятия управляемости и наблюдаемости.
Учебный материал Структурные схемы локальных систем в векторно-матричной форме
Если система имеет сигнал на входе и выходе в векторной форме, то в систему входит несколько исполнительных и корректирующих устройств. Векторно-матричные уравнения, описывающие динамку системы, по своему написанию ничем не отличаются от соответствующих уравнений объектов. В них входят расширенные матрицы, в которых учитываются уравнения датчиков корректирующих и исполнительных устройств.
21

Большинство ЛСА можно привести к двум типовым структурам:
(*)
|
|
2 |
3 |
4 |
|
|
|
|
|
|
|
|
|
8 |
10 |
|||
|
1 |
|
|
5 |
|
|
6 |
|
|
|
7 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
||
а) |
|
|
|
|
|
11 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
|
|
5 |
|
|
|
|
|
5 |
|
11 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 

 5
5 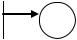

 6
6  7
7
12
11
б)
а) с отработкой ошибок от сигналов управления и возмущения, б) с комбинированным управлением и компенсацией ошибок.
На этих схемах управляющий сигнал 2 формируется в задающем устройстве 1. Он сравнивается в устройстве 3 с выходным сигналом, который измеряется датчиком 11.
В результате сравнения сигналов образуется сигнал разности 4, поступающий через устройства управления 5 и 6на объект регулирования 7. От действия сигнала 8, поступающего в систему через сумматор 9, происходит некоторое искажение выходного сигнала 10. Замыкание системы осуществляется главной обратной связи 12.
На рисунке (*), исключив задатчик, получим систему автоматической стабилизации, отрабатывающей сигнал возмущения.
Система на (*) под б) отличается тем, что в ней для получения более высокой точности применяются три 11-ых датчика, которые не только измеряют выходной сигнал 10, но и сигналы управления 2 и возмущения 8. Эти два сигнала, после прохождения устройства 5, поступают на сумматор 13 и уменьшают влияние сигналов на ошибку ЛСА.
Практически все ЛСА при решении задач синтеза и анализа сводится к этим двум схемам. При этом пользуются правилами преобразования структурных схем. Выделяют: линейную часть, нелинейную и цифровую части.
На ряду с передаточными функциями линейных элементов, используют эквивалентные передаточные функции дискретных нелинейных элементов. Для однозначных нелинейностей они совпадают с коэффициентами гармонической линеаризации.
Так как в современные ЛСА входят управляющие ЭВМ, то необходимо, для реализации вычислительных процедур, строить дискретные модели. Для определения дискретных моделей необходимо пользоваться последовательными реализуемыми на ЭВМ специальными программами.
Управляемость и наблюдаемость
22
Управляемость и наблюдаемость линейных и нелинейных замкнутых систем относятся к основным понятиям ТАУ, позволяющим оценивать правильность выполнения структурных преобразований. При этом следует иметь в виду, что управляющие сигналы g(t) должны переводить систему из любого начального состояния в установившееся за конечное время tk (управляемость), и по выходному сигналу x(t) однозначно определить еѐ начальное состояние (наблюдаемость).
Сформулируем понятие управляемости и наблюдаемости для любых систем, в которых протекают изменяемые во времени процессы x(t), эти процессы называются управляемыми, если на каждую переменную состояния y(t) можно целенаправленно воздействовать с помощью сигнала g(t) в течение конечного времени.
Если переменная состояния не зависит от управления g(t), то отсутствует возможность требуемого еѐ изменения во времени, и она является неуправляе-
мой.
Процесс g(t) называется наблюдаемым, если каждая переменная состояния процесса обуславливает изменение некоторых выходных переменных.
Графы состояний |
|
|
(1) |
|
|
g(t) |
y2 |
y2 |
y1 |
y1 |
x(t) |
|
S-1 |
1 |
S-1 |
|
1 |
|
-2 |
|
-3 |
|
|
а) |
|
|
|
|
|
g(t) |
y2 |
y2 |
y1 |
y1 |
x(t) |
1 |
S-1 |
|
S-1 |
|
1 |
|
-2 |
|
-3 |
|
|
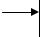
б)
На рисунке (1) изображена схема состояний процесса с 2-мя переменными y1 и
y2.
а) не полностью управляемой системой граф состояния, б) не полностью наблюдаемой системы граф состояния.
23
Так как входной сигнал g(t) воздействует не только на переменную y1(t), то переменное состояние y2(t) является не полностью управляемым или не управляемым.
Под пунктом б) изображена схема, соответствующая состоянию наблюдаемого процесса. Переменная состояния y2(t) не связана с выходной переменной x(t), поэтому, если x(t) измерена, то можно определить переменную y(t), поскольку
y1(t) = x(t).
Однако, по имеющейся информации об y1(t) нельзя определить переменную y2(t), значит, процесс можно охарактеризовать как не полностью наблюдаемый или не наблюдаемый.
Вопросы самоконтроля:
1.Порядок составления структурных схем ЛСУ в векторно-матричной форме.
2.Понятия управляемости и наблюдаемости.
ЛЕКЦИЯ №9 Цель лекции: Изучить порядок построения переходных процессов с помощью импульсных переходных функций.
Задачи лекции:
1.Порядок построения переходных процессов с помощью импульсных переходных функций.
2.Исследование динамической точности непрерывных и дискретнонепрерывных ЛСА
Желаемый результат:
Студенты должны знать:
1.Порядок построения переходных процессов с помощью импульсных переходных функций.
2.Исследование динамической точности непрерывных и дискретнонепрерывных ЛСА.
Учебный материал Построение переходных процессов с помощью импульсных переходных
функций
В случае действия ЛСА управляющего или возмущающего воздействия сложных форм, удобно пользоваться зависимостями, связывающими значение импульсной переходной функции замкнутой системы кз(t) с вещественной R(ω) и линейной S(ω) частными характеристиками:
|
|
j kз t e j tdt |
(1) |
0 |
|
Тогда, учитывая |
|
j R jS |
(2) |
получим:
24
|
|
|
R kз |
t cos tdt |
(3) |
0 |
|
|
|
|
|
S kз |
t sin tdt |
(4) |
0 |
|
|
Для вычисления интегралов (3) и (4) функцию кз представим в виде суммы элементарных трапеций кi(t), в этом случае выражения (3) и (4) примут вид:
n
R ki t cos tdt
i 0 0
n
R ki t sin tdt
i 0 0
Исследование динамической точности непрерывных и дискретнонепрерывных ЛСА
Динамическая точность ЛСА определяется ошибками, возникающими в системе от действия управляющих и возмущающих воздействий.
Все типы воздействий можно разделить на:
-регулярные,
-случайные,
-их комбинации.
Регулярные воздействия являются медленно – меняющимися функциями от времени, по сравнению с длительностью переходных процессов.
Ошибки от случайного воздействия определяются не мгновенными значениями, а еѐ средними квадратическими отклонениями.
Вопросы самоконтроля:
1.Переходные процессы с помощью импульсных переходных функций.
2.Динамическая точность непрерывных и дискретно-непрерывных ЛСА.
ЛЕКЦИЯ №10
Цель лекции: Изучить характеристики точности непрерывных ЛСУ при действии регулярных сигналов, определение характеристик точности дискретных и дискретно-непрерывных ЛСУ.
Задачи лекции:
1.Рассмотреть характеристики точности непрерывных ЛСУ при действии регулярных сигналов.
2.Рассмотреть характеристики точности дискретных и дискретнонепрерывных ЛСУ.
Желаемый результат:
Студенты должны знать:
1.Характеристики точности непрерывных ЛСУ при действии регулярных сигналов.
2.Характеристики точности дискретных и дискретно-непрерывных ЛСУ.
25
Учебный материал Характеристики точности непрерывных ЛСА при действии регуляр-
ных сигналов
Точность ЛСА при действии медленно – меняющихся регулярных сигналов определяется коэффициентом ошибок, которые можно получить разложением передаточной функции замкнутой системы относительно ошибки в ряд Макларена.
1. Неподвижное состояние
В качестве типового режима рассматриваются устойчивые состояния при постоянных значениях управляющего и возмущающего воздействия.
Ошибка системы в этом случае называется статической.
|
|
|
|
|
|
l |
p fk 0 |
|
|
|
|
|
|
|
g0 |
|
|
Wk |
|
|
|
|
|
x |
|
k 1 |
|
|
x/ |
x// |
|
||||
|
|
|
1 W p |
(1) |
|||||||
ст |
|
|
|
ст |
ст |
||||||
|
1 |
W p p 0 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p 0 |
|
|
|
где l – число возмущений g0 – управление
fk0 – возмущение
В статических режимах: W(0)=k – общий коэффициент усилия разомкнутой системы (цепи).
xст/ |
|
g0 |
; |
xст// |
1 f10 |
; |
|
k |
1 k |
||||
1 |
|
|
|
|||
где γ1 – коэффициент статизма
Величина (1+k) показывает эффективность регулирования с точки зрения уменьшения установленной ошибки.
Движение с постоянной скоростью
g(t)=υ(t); υ=const.
xуст |
|
xст |
xc xст |
(1) |
||||||||
|
|
|
||||||||||
h |
||||||||||||
|
|
|
|
|
|
|
|
|
||||
D ki |
|
|
|
– добротность по скорости. |
|
|||||||
xc |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
Движение с постоянным ускорением |
||
E const , |
g t t 2 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
xуст |
|
|
xст |
xy xст |
|
|||||||
|
|
|
|
|
||||||||
|
k |
|
||||||||||
|
|
|
|
|
|
|
|
|
||||
D k |
|
|
|
|
|
– добротность по ускорению. |
|
|||||
|
|
|
|
|
||||||||
|
|
xy |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
Движение по синусоидальному закону |
||
g t gmax sin k t – синусоидальный закон |
(2) |
|||||||||||
26

x gmax , max A k
где A(ωk) – модуль частотной ПФ разомкнутой ЛСА.
При ω=ωk.
Если управляющая функция времени g(t) имеет произвольную форму, но достаточно главную, чтобы иметь m производных вида:
dg |
; |
d 2 g |
;.....; |
d m g |
, |
|
dt |
dt 2 |
dt m |
||||
|
|
|
то ошибку ЛСА можно определить следующим образом (те же рассуждения пойдут к возмущениям).
Изображение ошибки: |
|
||||
x p x |
p G p |
|
G p |
|
(1) |
|
W p |
||||
|
1 |
|
|||
где Φх(р) – ПФ замкнутой системы по ошибке, G(р) – изображение управляющего воздействия.
Разложим ПФ по ошибке в ряд по возрастающим степеням Р:
|
|
|
C |
2 |
|
|
|
|
|
C |
3 |
|
|
|
|
|||
x p C0 |
C1 p |
|
p2 |
|
|
|
|
|
|
p3 |
... G p |
(2) |
||||||
2! |
|
|
3! |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
xуст C0 g t C1 |
dg t |
|
C |
2 |
|
|
d 2 g t |
..., |
(*) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
dt |
|
|
2! |
|
|
|
|
dt 2 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
сходящийся при малых р, т.е. при больших значениях t (установившееся значение).
Переходя к оригиналу, получаем формулу (*) для установившейся ошибки:
C0 x p p 0 ,C1 |
d x p |
|||
|
|
|
||
dp |
||||
|
|
|
||
|
d m |
x |
p |
|
||
|
,...Cm |
|
|
|
, |
|
|
dpm |
|||||
p 0 |
|
|
|
|||
|
|
|
|
p 0 |
|
|
где С0, С1, Ст - коэффициенты по ошибке. Их определяют согласно общему правилу расположение в ряд Тейлора.
Т.к. ПФ по ошибке представляет собой дробно-рациональную функцию, то коэффициенты ошибок можно наиболее просто получить делением числителя на знаменатель и сравнением полученного ряда с выражением (2).
В системах с астатизмом 1-го порядка:
C0=0, С1=1/kυ.
2-го порядка:
С0=0, С1=0, С2=1/kε.
При исследовании ошибки от возмущающего воздействия можно получить все коэффициенты ≠0 при астатизме любого порядка, т.к. астатизм по управляющему воздействию может соответствовать наличию статической ошибки по возмущению.
27
Определение характеристик точности дискретных и дискретнонепрерывных ЛСА
По аналогии с непрерывными системами ошибку можно представить в зависимости от ПФ Фε формой входного сигнала и его производной, значение которых известны только в тактовые моменты времени t=kT0. В этом случае ошибку можно представить следующим образом:
E kT0 C0 g kT0 |
|
C1 |
|
g kT0 |
C2 |
g kT0 |
|
C3 |
g kT0 ... |
(8.20) |
|||||||||||||||
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1! |
|
|
|
|
2! |
|
|
|
3! |
|
|
|
|||
x |
p |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
1 Wраз |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
1 |
|
|
d x |
p |
|
|
C2 |
d 2 x p |
|
|||||||||||||
C0 |
0 ; C1 |
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
||||
h |
|
dp |
2 |
|
dp |
2 |
|
|
|||||||||||||||||
|
|
|
|
|
p 0 |
|
|
|
|
p 0 |
|
||||||||||||||
Вопросы самоконтроля:
1.Перечислите характеристики точности непрерывных ЛСУ при действии регулярных сигналов.
2.Перечислите характеристики точности дискретных и дискретнонепрерывных ЛСУ.
ЛЕКЦИЯ №11 Цель лекции: Изучить порядок синтеза локальных систем управления.
Задачи лекции:
1.Порядок синтеза корректирующих устройств локальных систем управления всех типов.
Желаемый результат:
Студенты должны знать:
1.Порядок синтеза корректирующих устройств локальных систем управления всех типов.
Учебный материал Синтез ЛСА
Состоит в выборе структуры и параметров системы регулирования объектов, которые в соответствии с заданными ТУ обеспечивают наиболее рациональные характеристики по запасам устойчивости, показателям качества и точности. При проектировании, кроме того, необходимо учитывать множество дополнительных факторов: надѐжность, массу и габариты, стоимость, возможность работы при вибрации, в агрессивных средах, при значительных перепадах температуры и влажности.
Задачу синтеза можно решить 2-мя методами:
-если известна только динамика объекта, то выбирают структуру и параметры регулятора (или следящей системы).
-если одновременно с объектом задана структура регулятора (следящей системы) и динамические характеристики привода ИУ (неизменная часть), то в этом случае находят усилительное и корректирующее устройства системы.
28
Внепрерывных ЛСА используются корректирующие устройства на базе RCцепочек и дополнительных усилителей. При этом применяют последовательные, параллельные и последовательно – параллельные устройства.
Последовательные КУ вызывают повышенные частоты среза системы, и, следовательно, увеличивается влияние случайных сигналов, и при их использовании требуются двигатели большой мощности для управления исполнительными органами.
Параллельные КУ наоборот, снижают частоту среза fср ЛСА и делают еѐ малочувствительной к флуктуациям и помехам КУ данного типа, уменьшают влияние нелинейности во внутренних контурах системы.
Для устранения этих недостатков применяют одновременно последовательные и параллельные КУ.
Всовременных дискретных и дискретно – непрерывных ЛСА средства формирования запаса регулирования и КУ реализуются в виде рабочих программ на управляющих ЭВМ и МП.
Вопросы самоконтроля:
1.Перечислите порядок синтеза корректирующих устройств локальных систем управления всех типов.
2.Какие виды корректирующих устройств вы знаете..
ЛЕКЦИЯ №12 Цель лекции: Изучить порядок реализации корректирующих устройств в дискретных локальных системах управления.
Задачи лекции:
1.Порядок реализации корректирующих устройств в дискретных локальных системах управления.
2.Виды программирования корректирующих устройств локальных систем управления.
Желаемый результат:
Студенты должны знать:
1.Порядок реализации корректирующих устройств в дискретных локальных системах управления.
2.Виды программирования корректирующих устройств локальных систем управления.
Учебный материал Дискретно-непрерывные линейные и нелинейные системы.
Структурная схема исходной локальной системы разработана или полностью задана; в процессе проектирования найти законы регулирования, которые можно реализовать в виде последовательных, параллельных или последовательнопараллельных КУ в виде RC-цепочки или программы коррекции.
При проектировании дискретно-аналоговых систем необходимо подбирать параметры не только микропроцессора, но и преобразователей аналог-код, коданалог.
29

Значительное влияние на запасы устойчивости, показатели качества и характеристики точности оказывают такт квантования и длина слова. В случае несоответствия показателей качества и точности проводится коррекция системы с помощью RCцепочки или программы коррекции.
Используются 4-ре способа программирования:
1)прямое,
2)последовательное,
3)параллельное,
4)последовательно-параллельное.
Рассмотрим прямое программирование:
W z |
U |
z |
|
b b z 1 |
b2 z 2 |
... bn z n |
|
|||||
1 |
|
|
0 1 |
|
|
2 |
|
n |
(1) |
|||
U z |
|
1 a z 1 |
a |
z 2 ... a |
m |
z m |
||||||
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
При прямом программировании по передаточной функции (1) определяем разностное уравнение
n |
|
m |
|
|
U1* z bkU * t kT0 |
akU * t kT0 |
|
(2) |
|
k 0 |
|
k 1 |
|
|
|
|
|
||
U2* t |
|
U3* t |
|
|
уравнение (2) делится на две части: lp*(t)=U2*(t)-U3*.
Строится структурная схема программирования:
U*(t) |
|
U*(t-T0) |
|
U*(t-2T0) |
|
U*(t-mT0) |
|
1 |
2 |
3 |
|||||
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
e-STo |
|
e-STo |
e-STo |
|||
b0 |
b1 |
|
b2 |
|
bm |
||
U2*(t)
e*p(t)
U3*(t)
|
|
|
a1 |
|
a2 |
|
an |
|
e*p(t) |
e-STo |
|
e-STo |
|
e-STo |
|
|
|
1 |
|
2 |
|
3 |
|
|
||
|
|
|
|
|
|
|||
|
|
U1*(t-T0) |
U1*(t-2T0) |
U1*(t-nT0) |
||||
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
Последовательное программирование.
30
