
Лекции / Лекции по дисциплине ЛСУ
.pdf
Матрицы ~ и ~ являются периодическими с периодом Т.
a b
В случае однозначной нелинейности, матрицу коэффициентов линеаризации выбирают таким образом, чтобы минимизировать среднее значение квадрата разности между точным и приближѐнным сигналами на выходе.
|
|
|
t |
|
2 lim |
1 |
T |
|
t |
|
|
|
2 dt |
|
|
|
E |
|
|
E |
|
|
(8) |
||||||
|
|
|
|
|||||||||||
|
|
|
|
|
T 2T |
1 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
E1 t – значение по 1-й гармонике |
|
||||||||||||
E(t)=Y(x1)-a(x1)x1 |
|
|
|
|
|
|
(9) |
|||||||
в случае однозначной нелинейности |
|
|||||||||||||
a11 |
|
|
|
|
|
|
|
||
x2 |
|||||||||
|
|
|
11 |
|
|
||||
|
|
|
|
|
|
|
|||
a12 |
x11x12 |
||||||||
. |
|
. |
|||||||
|
|
|
|
|
|
|
|
||
. |
|
. |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
a1n |
|
x11x1n |
|||||||
an1 |
|
|
|
|
|
||||
|
x2 |
||||||||
an2 |
|
x x |
|||||||
|
|
|
|
|
11 |
|
|||
|
|
|
11 12 |
||||||
. |
|
. |
|||||||
|
|
|
|
|
|
|
|
||
. |
|
. |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
ann |
x11x1n |
||||||||
x12x11 . .
x2 |
. . |
11 |
|
. |
. . |
. |
. . |
x12 x1n . .
x12 x11 . .
x2 |
. . |
12 |
|
. |
. . |
. |
. . |
x12 x1n . .
|
|
|
|
|
|
1 |
|
|
|
|
|
|
||||||||
x x |
F x |
|
||||||||||||||||||
11 |
11 |
|
|
|
|
|
1 |
11 |
|
|
||||||||||
x1n x12 |
|
F1x12 |
|
|
||||||||||||||||
. |
|
|
|
|
|
. |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
. |
|
|
|
|
. |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
2 |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
x1n |
|
F1x1n |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|||||||||
|
x |
x |
|
|
F x |
|
||||||||||||||
|
|
1n |
|
11 |
|
|
|
1 |
11 |
|
||||||||||
|
x1n x12 |
F1 x12 |
||||||||||||||||||
. |
|
|
|
|
|
|
|
. |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
. |
|
|
|
|
|
. |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
x1n |
|
|
|
F1 x1n |
|||||||||||||
Пусть на вход нелинейности поступает первая гармоника синусоидального сигнала:
x1 t A sin t Asin |
|
|
|
(10) |
||
1 |
2 |
|
|
|
|
|
a A |
|
F A sin sin d |
|
|
(11) |
|
A |
|
|
||||
0 |
0 |
|
|
|
|
|
F – приближенное значение передаточной функции по 1-ой гармонике. |
||||||
В случае двузначной нелинейности: |
|
|||||
|
|
|
b x , x |
x |
|
|
E t F x1 , x1 a x1 , x1 x1 |
|
1 |
|
|
||
1 1 |
|
(12) |
||||
2 k |
|
|||||
|
|
|
|
|
|
|
Е – разность между истинным и приближенным значениями сигналов.
|
|
|
2 |
n |
n |
b x , x x T |
||
|
|
|
|
|
|
1 1 ij |
|
|
E t |
|
Fi |
x1 , x1 aij x1 , x1 xij |
|
(13) |
|||
|
2 k |
|||||||
|
|
|
|
|
j 1 |
|
|
|
|
|
|
|
i 1 |
|
|
||
11

a11 |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
x |
2 |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
11 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
a12 |
|
x11x12 |
|
||||||||||||||||
|
. |
|
|
|
. |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
. |
|
. |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
a1n |
|
x11x1n |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b11 |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
x |
2 |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
11 |
|
|
|
|
||||||
b12 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
x |
|
|
|
x |
|
||||||||||||||
|
|
|
|
11 |
|
12 |
|
|
|||||||||||
|
|
. |
|
||||||||||||||||
. |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
. |
|
. |
|
||||||||||||||||
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
x |
|
|
|
x |
|
||||||||||||
1n |
|
|
11 |
|
1n |
|
|||||||||||||
an1 |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
x2 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
11 |
|
|
||||||||
an 2 |
|
|
|
|
|
|
|||||||||||||
x |
|
x |
|
||||||||||||||||
|
|
|
|
|
11 12 |
|
|||||||||||||
. |
|
|
|
|
|
|
. |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
. |
|
. |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
ann |
x11x1n |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
bn1 |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
x |
2 |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
11 |
|
|
|
|||||||
bn 2 |
|
|
|
|
|
||||||||||||||
x |
|
x |
|
||||||||||||||||
|
|
|
|
|
11 |
12 |
|
||||||||||||
|
|
. |
|
||||||||||||||||
. |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
. |
|
. |
|
||||||||||||||||
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
b |
|
x |
|
x |
|
||||||||||||||
nn |
|
|
|
11 |
1n |
|
|||||||||||||
x12 x11 . .
x2 |
. . |
11 |
|
. |
. . |
. |
. . |
x12 x1n . .
x12 x11 . .
x2 |
. . |
11 |
|
. |
. . |
. |
. . |
x12 x1n . .
x12 x11 . .
x2 |
. . |
12 |
|
. |
. . |
. |
. . |
x12 x1n . .
x12 x11 . .
x2 |
. . |
12 |
|
. |
. . |
. |
. . |
x12 x1n . .
|
|
|
|
1 |
|
|
|
|
|
||
x |
x |
F x |
|||||||||
11 |
11 |
|
|
|
1 11 |
|
|
||||
x1n x12 |
|
F1 x12 |
|
|
|||||||
. |
|
|
|
. |
|
|
|
||||
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|||||
. |
|
|
. |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
||
2 |
|
|
|
||||||||
|
|
|
|
|
|||||||
|
x1n |
|
F1 x1n |
|
|
||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
||||||||
x11x11 |
|
|
|
|
||||||||||||||||
|
|
F1 x11 |
|
|
||||||||||||||||
x1n x12 |
F1 x12 |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
. |
|
|
|||||||||||||
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||
. |
|
|
|
. |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
2 |
|
|
|
|
|
|
|
|||||||||||||
|
|
x1n |
|
F1 x1n |
|
|
||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|||||||
|
x x |
|
|
F x |
|
|
||||||||||||||
|
|
1n 11 |
|
|
|
n 11 |
|
|
||||||||||||
|
x1n x12 |
Fn x12 |
||||||||||||||||||
. |
|
|
|
|
|
|
. |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
. |
|
|
|
|
|
. |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
2 |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
x1n |
|
|
|
Fn x1n |
|||||||||||||
|
|
1 |
|
|
|
|
|
x1n x11 |
|
||||||
|
|
Fn x11 |
|
||||
x1n x12 |
Fn x12 |
|
|||||
|
|
|
|
|
|
|
|
. |
|
|
|
. |
|
|
|
|
|
|
|
|
|||
|
|
|
|
||||
. |
|
|
. |
|
|||
|
|
|
|
|
|
|
|
2 |
|
|
|||||
x1n |
|
Fn xn |
|
||||
Определим коэффициенты линеаризации двузначной нелинейности, когда на еѐ вход поступает первая гармоника синусоидального сигнала, и имеется один выход. Из матрицы получаем коэффициенты гармонической линеаризации.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
a x1 |
F x1 x1 |
(1) |
|||||||||||||||
|
|
x 2 |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
1 |
|
x1 |
|
|
|
|
|
|||||
|
|
|
2 |
|
|
|
|
|
|||||||||
b x1 |
|
|
F |
x1 |
(2) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
||||
|
T |
|
|
|
|
|
x |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
||
x1 t A sin t A sin |
(3) |
||||||||||||||||
a x |
|
1 |
|
|
|
|
2 E A sin sin d |
|
|||||||||
AT |
|
|
|
|
|||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
(4) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|||
12

b x |
1 |
2 E A sin cos d |
|
AT |
|
||
1 |
|
(5) |
|
|
|
||
|
|
0 |
|
Y A a A jb A |
(6) |
||
Классическая теория гармонической линеаризации типичных нелинейностей предполагает, что сигнал, снимаемый с выхода нелинейностей, является периодическим и имеет основную частоту, совпадающую с частотой синусов входного сигнала. В результате такого допущения, при нахождении эквивалентных передаточных функций или коэффициентов гармонической линеаризации, учитывают только первую гармонику, а влиянием высших гармоник - пренебрегают. Это справедливо лишь для таких систем, линейная часть которых является низкочастотной и подавляет колебания высоких частот.
Пусть на вход однозначной нелинейности поступает сигнал: |
|
x1 t A sin t |
(7) |
На выходе: y t F A sin t |
(8) |
И приближѐнное значение выходного сигнала: |
|
y1 t A1 sin t |
(9) |
А1 – первая гармоника сигнала на выходе нелинейности.
Приближѐнное значение выходного сигнала через коэффициенты гармонической линеаризации:
y1 |
t Aa A sin t |
|
|
|
(10) |
|||||||||||
y1 |
t a A x1 t |
|
|
|
(11) |
|||||||||||
a A |
|
y |
t |
|
|
|
|
|||||||||
|
1 |
|
|
|
|
|
|
|
|
(12) |
||||||
|
x1 |
t |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
||||||||
или |
a A |
|
A1 |
|
|
|
|
|
||||||||
|
A |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Или коэффициенты усиления. |
|
|||||||||||||||
При двузначной нелинейности: |
|
|||||||||||||||
y1 |
t |
С1 sin t 1 |
|
(13) |
||||||||||||
y1 |
t A1 sin t B1 cos t |
(14) |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
C |
|
A2 |
B2 |
|
|
|
|
|||||||||
1 |
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|||
sin 1 |
|
A1 |
|
, cos 1 |
|
B1 |
|
|
||||||||
|
C |
|
C |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
y1 t a A Asin t Ab A cos t |
(15) |
|||||||||||||||
а(А), b(А) – коэффициенты гармонической линеаризации по 1-ой гармонике. |
||||||
y t a A x |
t |
b A |
x t |
(16) |
||
|
||||||
1 |
1 |
|
A |
1 |
||
|
|
|
|
|
|
|
Y A a A jb A |
или Y A qae j A |
(17) |
||||
j, μ(A) – амплитудная и фазовая характеристики по 1-ой гармонике. |
||||||
q A |
|
|
|
|||
a2 A b2 A |
(18) |
|||||
13
A arctg |
b A |
|
|
|
|
|
|
(19) |
|
a A |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||
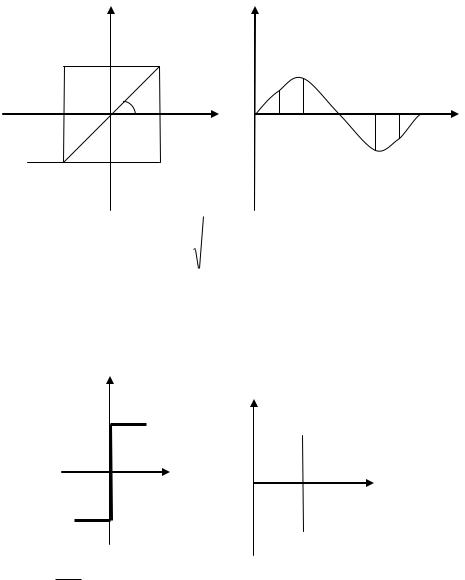
Пример: |
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
y |
|
||
|
|
в |
|
|
|
|
|
|
|
-а |
0 |
|
β а |
0 |
π |
π+φ1 |
|||
|
|
|
|
|
|
x |
φ π-φ1 |
2π |
|
|
|
|
|
|
|
|
|||
-в
|
2k |
C |
|
C |
|||
a A |
|
arcsin |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
A |
|
A |
|
|
|
|
|
|
|
|
|
А>>С
k – тангенс угла наклона k=tgβ
|
|
|
|
|
|
|
|
C |
2 |
|
|
|
|
|
|||
1 |
|
|
|
|
|
|
2 |
||||
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Статическая характеристика |
|
|
|
|
|
|
|
y |
|
Выходной сигнал |
|||
|
B |
|
|
y |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
x |
|
|
π |
2π |
||
|
0 |
|
||||
|
|
|
|
|
φ |
|
|
|
|
|
|
|
|
|
-B |
|
|
|
|
|
|
|
|
|
|
|
|
a A 4B A
Для МП W=1
Далее от W(p)=>W(z)
|
1 |
|
z 1 |
W p |
|||
W z |
|
|
|
|
Z |
|
|
2 |
|
z |
p |
||||
|
|
|
|
||||
14

y
|
|
B |
-C |
0 |
C |
|
|
x |
|
-B |
|
x0
y1(t)=F(x0,A)+Aa(x0,A)·sinωt+Ab(x0,A)cosωt
F(x0,A), Ab(x0,A), Aa(x0,A) – варианты этих величин, в зависимости от их смещения, представлены в справочниках.
В случае использования в системе нелинейных элементов, имеющих статические характеристики со смещением, необходимо учитывать при линеаризации дополнительные гармонические составляющие автоколебаний. При этом эквивалентная передаточная функция зависит от двухчастотного или многочастотного сигнала. Использование таких эквивалентных передаточных функций в нелинейных системах целесообразно, когда требуется оценить влияние высших гармоник на появление автоколебаний.
Вопросы самоконтроля:
1.Перечислите виды существующих нелинейных объектов управления ЛСУ?
2.Рассмотрите математическое описание коэффициентов линеаризации нелинейных объектов ЛСУ?
3.Рассмотрите математическое описание коэффициентов линеаризации двузначных нелинейных объектов ЛСУ?
ЛЕКЦИЯ №5 Цель лекции: Изучить порядок синтеза ЛСУ, элементный синтез, метрологи-
ческий синтез, энергетический синтез, временной синтез, разделительный синтез.
Задачи лекции:
1.Порядок синтеза ЛСУ.
2.Выбор и обоснование каждого звена ЛСУ по предыдущим критериям.
Желаемый результат:
Студенты должны знать:
1.Порядок синтеза ЛСУ;
2.Выбор и обоснование каждого звена ЛСУ по предыдущим критериям.
15
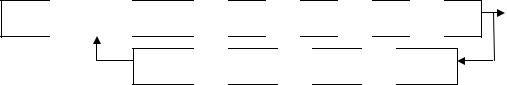
Учебный материал Элементный синтез
Исходя из принятого технического задания, выбираются элементы или звенья ЛСУ по их размерности. Выбор ведѐтся справа налево.
Синтез начинается с ОУ.
З
 ЦАП
ЦАП  У
У  Д
Д  Р
Р  Кв
Кв
АЦП  НУ
НУ  ТД
ТД  МПр
МПр
Кв - конвейер винтовой, Q [кг/с]; Р – редуктор, ω [рад/с]; Д – двигатель, ω1 [рад/с];
У – усилитель, U [B];
З – задающее устройство, U2 [B];
МПр – механический преобразователь, Р [Па]; ТД – тензодатчик, Rx [Ом];
НУ – нормирующий усилитель, Uн [В].
В качестве З можно использовать таймер, реле и микропроцессор.
Для постоянства массы в упаковке надо регулировать время упаковки. В этом случае обратную связь надо делать по параметрам, связанными со временем. m[кг]=[кг/м2]*[м/с]*[с]*[м];
Это вариант четырѐхконтурного регулирования по четырѐм параметрам: давление на поверхности конвейера (дозатор), скорость перемещающейся ленты, время насыщения, линейное перемещение ленты конвейера.
Регулирование может вестись по одному параметру, все остальные, при этом – постоянные. Если учесть, что нестабильность присутствует в любой ЛСУ, регулирование можно вести по всем четырѐм параметрам.
Выберем контур с изменением давления на поверхности конвейерной ленты, поскольку в качестве привода выбран электродвигатель. Регулировать будем скорость перемещения, а измерять – давление.
Метрологический синтез
На этом этапе создаѐтся по ТЗ метрологическая точность объекта управления. Метрологическая точность ОУ на входе определяется с помощью статической характеристики относительных единиц. Дальше рассчитывается погрешность всех звеньев ЛСУ, допустимый диапазон абсолютных значений параметров, который соответствует выбранной в ТЗ погрешности.
Энергетический синтез
Соседние по функциональной схеме звенья должны отвечать оптимальным критериям согласования нагрузок: выходная мощность предыдущего звена не должна быть меньше входной мощности последующего звена.
Пример:
Рассмотрим ЛСУ сыпучих материалов.
16

- Кв : 25 кг за 5 с, тогда Nвых |
|
mgl |
|
25 10 0,8 |
40Вт. |
|
t |
5 |
|||||
|
|
|
|
-Мпр: его кпд <1, тогда примем N=42Вт.
-ТД: на резисторе тензодатчика выделяется мощность
N=I2Rx=(10-3)2·100=10-4 Вт,
Где I – ток в цепи НУ,
Rx – предел измерения ТД.
Таким образом, задача ставится так: какой мощности нужно выбрать резистор ТД, чтобы при воздействии на него 42Вт механического усилия, он выдержал то воздействие.
Перед выбором ТД нужно выбрать подложку; после выбора подложки выбирается мощность ТД.
- НУ: мощность на выходе НУ может определяться 2-мя способами:
а) выбирается стандартный НУ; выходная мощность берѐтся из справочника, и под него выбирается АЦП, также его можно сделать самостоятельно.
б) предпочтительнее найти параметры предполагаемого АЦП и мощность выходного сигнала N=I·U, исходя из этого, выбираются или рассчитываются
начальные условия: К Nвых 0,01Вт.
Nвх
-АЦП: поскольку в принципе АЦП, ЦАП задатчик находится внутри процессора, то вопрос энергетического подбора этих звеньев пропускается, энергетика определяется параметрами микропроцессора.
-Р: примем, с учѐтом потерь на тепло, N=43Вт.
-Д: примем N=45Вт.
-У: допустим, что в качестве Д выбран ИДПТ с независимым управлением, Кд
=10, тогда при U1 = 5В, Ку =5/10-2 =500.
Таким образом, проведена вся цепь.
Временной синтез
Синтез также проводится справа налево, как в прямой цепи, так и по обратной. При движении влево должен наблюдаться принцип увеличения быстродействия.
В нашем примере наибольшим быстродействием обладает микропроцессор. Если соблюдается принцип наращивания мощности, КN =1,1, то коэффициент изменения быстродействия К=1/ КN.
Разделительный синтез
В процессе синтеза могут возникнуть ситуации, когда каждое из звеньев может потребовать коррекции, то есть само звено может являться ЛСУ и требовать цифровой коррекции. Часть цифровой ЛСУ может быть дополнена элементами непрерывной части, которые могут появиться в результате выбора каждого из элементов.
Полностью цифровых ЛСУ принципиально быть не может, так как есть звенья, работающие только в непрерывном режиме.
Поскольку цифровые звенья имеются в любой ЛСУ, то анализ и синтез проводится в цифровой форме.
17
Выбор и обоснование каждого звена ЛСУ по предыдущим критериям
Из этих критериев основными являются все, но есть особенности: в элементном синтезе не допускаются нарушения размерностей, а метрологический, энергетический, временной и разделительные синтезы являются альтернативными.
Вопросы самоконтроля:
1.Перечислите порядок синтеза ЛСУ.
2.Рассмотрите элементный синтез.
3.Рассмотрите метрологический синтез.
4.Рассмотрите энергетический синтез.
5.Рассмотрите временной синтез.
6.Рассмотрите разделительный синтез.
ЛЕКЦИЯ №6 Цель лекции: Изучить порядок составления математической модели каждого
звена ЛСУ, краткий алгоритм получения математической модели с помощью системы с распределенными параметрами.
Задачи лекции:
1.Порядок составления математической модели каждого звена ЛСУ.
2.Краткий алгоритм получения математической модели с помощью системы с распределенными параметрами.
Желаемый результат:
Студенты должны знать:
1.Порядок составления математической модели каждого звена ЛСУ.
2.Краткий алгоритм получения математической модели с помощью системы с распределенными параметрами.
Учебный материал Математическая модель каждого звена
Все мат. Модели делятся на два класса:
1)Системы с сосредоточенными параметрами, если быстродействие звена на 1- 2 порядка превышают быстродействие ОУ.
2)Системы с распределѐнными параметрами. Если в звене есть время запаздывания, соизмеримое с постоянной времени ОУ.
В нашем примере к СРП могут быть отнесены: редуктор, электродвигатель лента конвейера.
Краткий алгоритм получения модели в СРП.
1. Выбирается дифференциальное уравнение из справочника Бутковского. а) «Гитарист» – одномерные задачи (колебание струи).
б) «Барабанщик» – двумерные задачи (колебание мембраны). в) «Пекарь» – трѐхмерные задачи.
2. Для выбранного уравнения выбирается континуальная передаточная функция.
3. Для выбранной континуальной передаточной функции строят ЛАЧХ и аппроксимируют еѐ типовыми звеньями.
18
4.Полученную передаточную функцию считают как ССП, где есть только один вход и один выход. Дальше она используется для расчѐта ЛСУ в целом.
5.Если предыдущие пункты выполнены для каждого звена, то полученная ЛСУ будет желаемой, то есть еѐ не нужно корректировать.
Вопросы самоконтроля:
1.Перечислите порядок расчета передаточных функций элементов ЛСУ.
2.Перечислите порядок расчета передаточных функций элементов ЛСУ с помощью системы с распределенными параметрами.
ЛЕКЦИЯ №7 Цель лекции: Изучить порядок проведения статической линеаризации нели-
нейных элементов ЛСУ, порядок проведения совместной статической и гармонической линеаризации нелинейных элементов ЛСУ.
Задачи лекции:
1.Статическая линеаризация существенных нелинейных элементов.
2.Совместная гармоническая и статическая линеаризация.
3.Существенные дискретные нелинейные элементы.
Желаемый результат:
Студенты должны знать:
1.Порядок проведения статической линеаризации существенных нелинейных элементов.
2.Порядок проведения совместной гармонической и статической линеаризации нелинейных элементов.
3.Понятия существенных дискретных нелинейных элементов.
Учебный материал Статическая линеаризация существенных нелинейных элементов.
В системах автоматического регулирования в реальных условиях на вход существенных нелинейных элементов, наряду с детерменированными, поступают и случайные сигналы. Существующие строгие методы анализа нелинейных систем со случайными сигналами требуют учѐта законов распределения случайных величин, что приводит к сложной математике.
В инженерной практике пользуются приближѐнным методом – методом статической линеаризации, сущность которого состоит в замене нелинейного эле-
мента статически – линеаризованным, то |
есть нелинейную характеристику |
y(t)=F(x) (1) заменяют линейной: |
|
yл t k0mx k1 x t |
(2) |
mx – математическое ожидание
k0 – коэффициент по математическому ожиданию x t x t mx
k1 – коэффициент по этой составляющей
Значения к0 и к1 подбираются таким образом, чтобы добиться максимального приближения yл к y.
19
Пусть на вход двузначной нечастотной симметричной нелинейности поступает сигнал:
x1(t)=A1·sin(ωt)+A3sin(3ωt+φ3) |
(1) |
|
A1·sin(ωt) – 1-ая гармоника, A3sin(3ωt+φ3) – 3-я гармоника |
|
|
φ3 – сдвиг по фазе 3-ей гармоники |
|
|
y1(t)=F(A1·sin(ωt)+A3sin(3ωt+φ3)) |
(2) |
|
y1(t) – функция от входного сигнала. |
|
|
Запишем (2) через коэффициенты линеаризации: |
|
|
y1(t)=A[a1(A)·sin(ψ)+b1(A)·cosψ+a3(A)·sin(3ψ+φ3)+b3(A)·cos(3ψ+φ3)] |
(3) |
|
a1, b1, a3, b3 – коэффициенты линеаризации по 1-ой и 3-ей гармонике |
|
|
Совместная гармоническая и статическая линеаризация. |
|
|
При поступлении на вход нелинейного элемента суммы 2-х сигналов |
|
|
x t mx t x t Asin t |
(1) |
|
|
|
|
Можно считать, что коэффициенты статической линеаризации являются периодическими функциями времени.
Применив совместную статическую и гармоническую линеаризацию, получим
приближѐнную зависимость: |
Asin k1 * A,mx , x |
x t |
(2) |
|||||||||||
y t F0 |
* A,mx , x |
a * A,mx , x |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F * A, m , |
|
|
1 |
2 F m Asin , d |
|
|
||||||||
|
|
2 |
|
|
||||||||||
0 |
x |
x |
|
|
|
|
x |
x |
|
(3) |
|
|||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
a * A, mx , x |
|
|
1 |
|
2 F mx Asin , x sin d |
(4) |
|
|||||||
2 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
k * A, m , |
|
|
1 |
|
2 F m Asin , cos d |
|
|
|||||||
|
|
2 |
|
|
||||||||||
1 |
x |
x |
|
|
|
|
x |
|
x |
(5) |
|
|||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
Существенные дискретные нелинейные элементы
Нелинейные импульсные элементы для удобства математического описания можно представить в виде совокупности линейного и нелинейного элемента.
y(kT0)=F[x(t)]δ(t), (1) y – сигнал на выходе
|
|
|
|
|
|
|
|
|
|
где t t kT0 |
|
|
|
|
|
|
|||
|
k |
|
|
|
|
|
|
|
|
входной сигнал является гармоническим: |
|
|
|
||||||
x(t)=Asin(ωt+φ), |
|
|
|
|
|
(2) |
|
||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
nT0 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||
nT0 – полупериод гармонического колебания |
|
|
|
||||||
y1(kT0)=F[Asin(ωt+φ)]δ(t) |
|
|
|
(3) |
|
||||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
(4) |
|
|
|
|
|
|||||
y1 kT0 A a A, n, sin |
|
b A, n, cos |
|
t |
|||||
|
|
nT0 |
|
nT0 |
|
|
|||
20
