2.3. Время движения частицы жидкости, движущейся по радиусу от контура питания к скважине

Истинная скорость движения в точке N (см. рис. 2.2) будет равна

(2.13)

Здесь принят знак (‑), т. к. функция dr убывающая. Разделив переменные и проинтегрировав (2.13), получаем

(2.14)

При t=0 имеем r=R_к, т. е.

(2.15)

Тогда

(2.16)

Получили формулу закона движения частицы. При r=r_c получим время прохождения частицы от точки N до забоя скважины.

4. Стоки и источники на плоскости

Вводя удельный расход и учитывая, что ds=-dr, получаем следующее выражение для скорости фильтрации

(2.17)

Интегрируя (2.17), находим

. (2.18)

Получили очень важную формулу потенциала точечного стока на плоскости. Как видим, потенциал в окрестности скважины пропорционален логарифму расстояния r от скважины. Точечным стоком называют скважину бесконечно малого радиуса, хотя в природе такой скважины не существует. В гидродинамике эксплуатационную скважину принимают за точечный сток (q>0), а нагнетательную – за точечный источник (q<0) и называют их соответственно: скважина-сток и скважина-источник.

Исследуем (2.17) и (2.18). При r=0 значения Ф и обращаются в ¥; при r=¥ значение Ф=¥, а =0. Таким образом, формулы (2.17) и (2.18) имеют физический смысл всюду, кроме r=0 и r=¥.

Итак, плоские задачи фильтрации эффективно могут быть решены с помощью потенциала. Пусть на плоскости известны потенциалы Ф_к и Ф_с на двух концентрично расположенных окружностях с радиусами R_к и r_с (рис. 2.4).

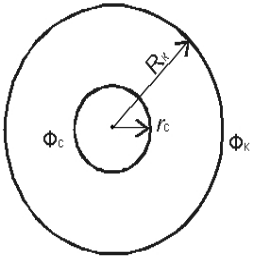
Рис. 2.4. Схемы притока к стоку (источнику) на плоскости

Согласно (2.18) имеем:

,

,

откуда следует:

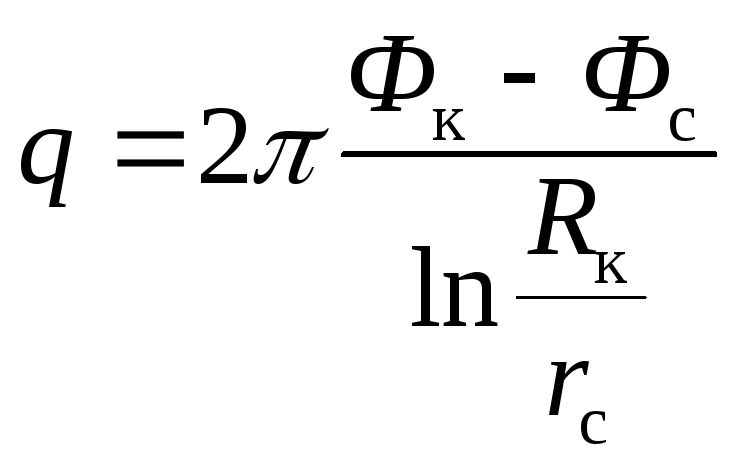. (2.19)

Переходя от потенциала к давлению в (2.19), получим формулу Дюпюи (2.10).

4. Стоки и источники в пространстве

Рассмотрим задачу о потенциале точечного стока в пространстве. В этом случае приток будет радиально-сферический (рис. 2.5). По закону Дарси имеем

С другой стороны, можно записать

где f=4pr² – площадь фильтрации сферы.

Приравнивая указанные выражения и интегрируя, получаем

(2.20)

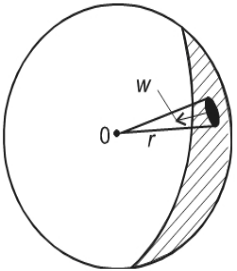
Рис. 2.5. Схема радиально-сферического притока

Получили формулу потенциала точечного стока в пространстве. При r=0 имеем Ф=-¥, u=¥; при r=¥ получаем Ф=const, u=0. Покажем использование формулы (2.20). Пусть Ф_к и Ф_с потенциалы на сферах, описанных радиусами R_к и r_с. Согласно (2.20) имеем:

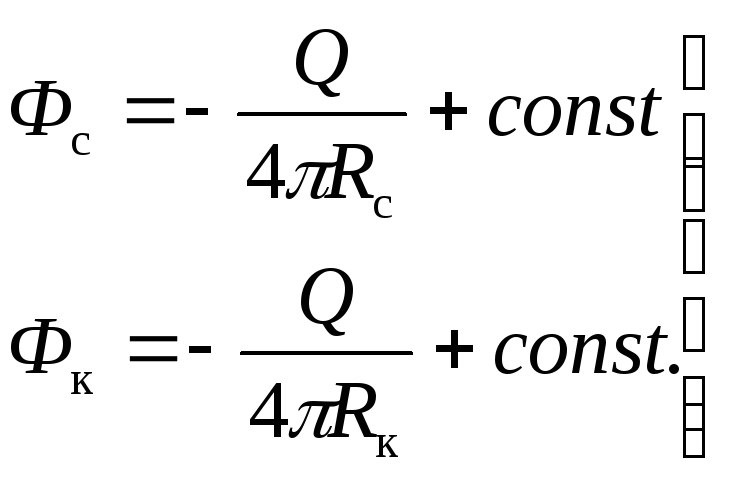(2.21)

По правилу производных пропорций из (2.21) имеем

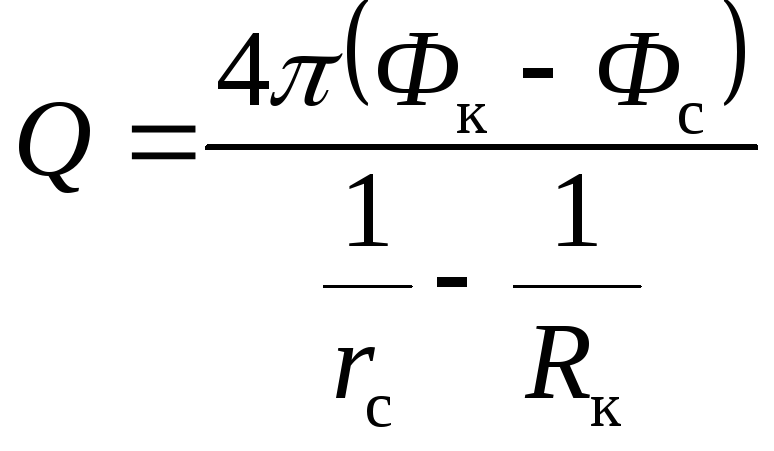. (2.22)

При r®¥ const в (2.20) становится потенциалом на бесконечности. Обычно , следовательно, .

Тогда

. (2.23)

Таким образом, для точечного стока в пространстве радиус контура питания практически на дебит не влияет. В случае плоскорадиального притока (формула Дюпюи) ошибка в выборе в 2-3 раза к большим погрешностям в дебите не приведет. Для полупространства (рис. 2.6), например, пласт большой толщины, где вскрыта только кровля пласта, формула (2.22), очевидно, запишется в виде

. (2.24)

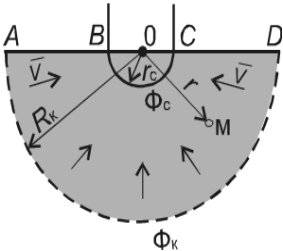
Рис. 2.6. Схема радиально-сферического притока в полупространстве

(скважина вскрыла лишь кровлю пласта)