Безнапорной фильтрации через прямоугольную перемычку
Горизонтальная компонента скорости фильтрации
(5.2)
Эта компонента предполагается постоянной вдоль вертикали. Вертикальная компонента по условию равна нулю.
Расход на единицу ширины потока f=1 запишется выражением
(5.3)
Итак мы видим, что отличительным признаком безнапорного движения является линейная зависимость потенциала или функции Н на свободной поверхности от вертикальной координаты Z.
5.2. Гидравлическая теория безнапорного движения через прямоугольную перемычку на горизонтальном основании
Определим из (5.3) уравнение свободной поверхности. Разделяя переменные и интегрируя, получим
(5.4)
Используя граничные условия (см. рис. 5.1)
(5.5)
находим
(5.6)
(5.7)
Решая совместно (5.6) и (5.7), находим расход
(5.8)
Подставляя (5.6) в (5.4) и учитывая (5.8), находим
(5.9)
Получили
уравнение параболы. Таким образом,
поверхность депрессии является параболой
(линия АС,
рис 5.1). В действительности формула (5.9)
несправедлива. Это видно из следующих
соображений. При Р2=0
у выхода в нижний бьеф (х=l)
из формулы (5.9) получаем, что h=0.
Это приводит к бесконечной скорости
фильтрации
что невозможно. Поэтому необходимо,
чтобы выполнялось условие hx=l>H2,
т. е. должен существовать промежуток
высачивания.
Формула Дюпюи (5.8), хотя и выведена из допущений гидравлической теории, является строго точной. Строгое доказательство ее дано И.А. Чарным [5].
5.3. Гидравлическая теория безнапорного притока к совершенной скважине
Рассмотрим приток к совершенной скважине. Все обозначения даны на рис. 5.2. Движение считаем установившимся, т. е. Q и h=h(r) от времени не зависят. Скважину считаем стоком, следовательно, дебит будет положительным.
Скорость фильтрации по закону Дарси
(5.10)
Если f=2prh — площадь фильтрации при плоскорадиальном притоке, то дебит скважины выразится формулой
(5.11)
Знак минус здесь не ставим, так как мы рассматриваем скважину сток, а функция h=h(r) является возрастающей функцией расстояния.
Разделяя переменные в уравнении (5.11) и интегрируя, получаем
(5.12)
Из граничного условия h=Hк при r=Rк находим
(5.13)
Подставляя (5.13) в (5.12), найдем уравнение свободной поверхности (АСС'A', рис. 5.2). Используя второе граничное условие h=Hc при r=rc и выражение (5.13), из (5.12) получаем формулу Дюпюи
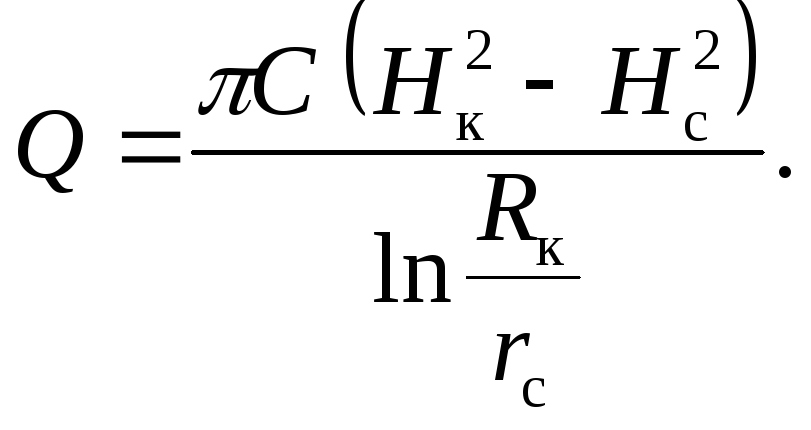(5.14)
Формула (5.14), как и формула (5.8), является строго точной.
5.4. Дифференциальные уравнения гидравлической теории нестационарной безнапорной фильтрации
Согласно гидравлической теории безнапорного движения считается, что напор Н=Н(х, у, z, t) является постоянной величиной вдоль каждой вертикали, а горизонтальные проекции скорости фильтрации u, u равномерно распределены вдоль каждой вертикали. Тогда напор равен глубине потока (Н=h) и компоненты скорости запишутся в следующем виде:
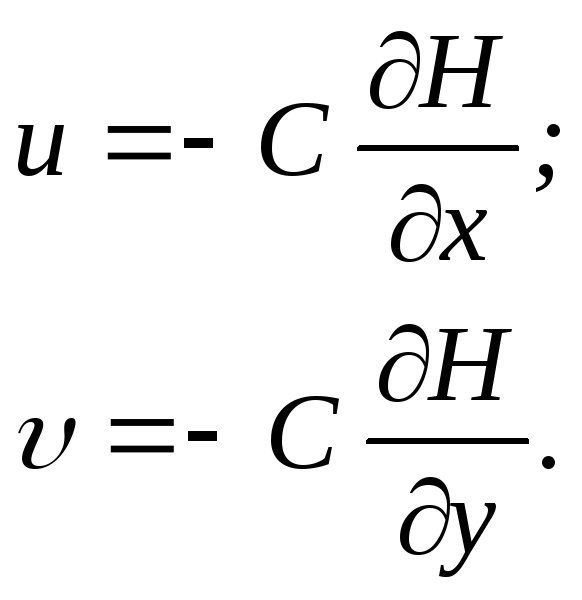(5.15)
Расходы потока на единицу ширины в направлениях х и у соответственно будут равны:
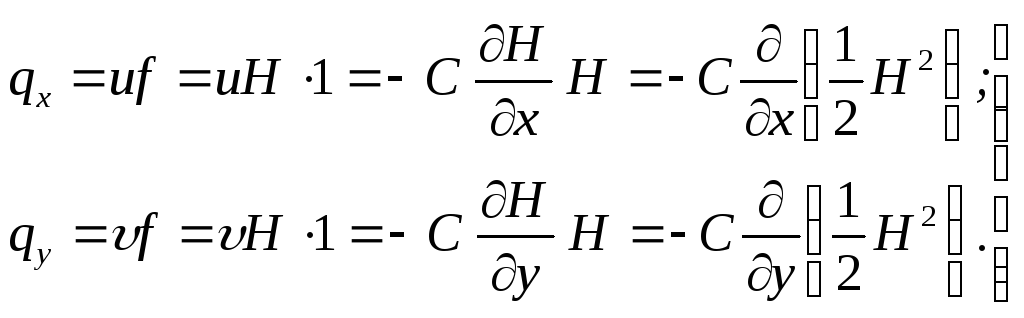(5.16)
Составим уравнение неразрывности для нестационарного грунтового потока. Выделим элемент грунта высотой Н=h и площадью сечения dxdy (рис. 5.4). За время dt в параллелепипед поступает
Вытекает за то же время
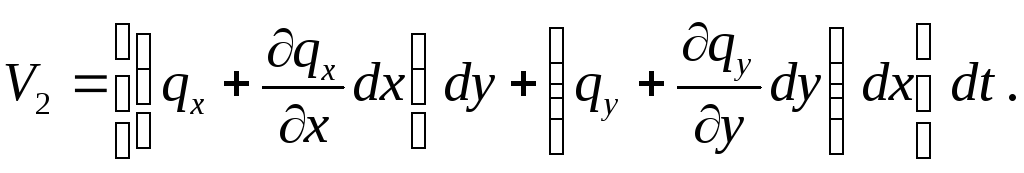
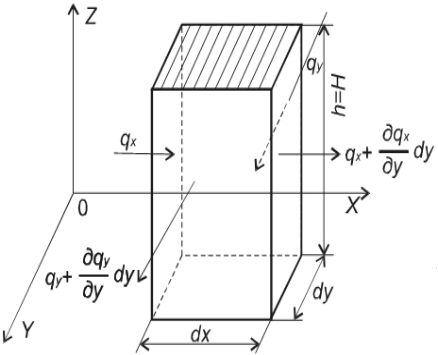
Рис. 5.4. Схема к выводу уравнения гидравлической теории
Следовательно, накопленный объем за время dt составит
(5.17)
Этот
объем идет на повышение высоты Н,
которая за время dt
меняется на величину
Учитывая пористость т,
изменение объема можно записать еще в
таком виде
(5.18)
Приравнивая (5.17) и (5.18), находим
(5.19)
Подставляя значение qx и qy из (5.16) в (5.19), получим
(5.20)
или
(5.21)
Получили дифференциальное уравнение гидравлической теории нестационарного безнапорного потока Буссинеска. Как видим, уравнение это нелинейное параболического типа в частных производных. В общем случае точного решения не имеет. Точные решения для частных случаев имеются у П.Я. Полубариновой-Кочиной.
Одним из методов приближенного решения подобных уравнений является метод линеаризации Л.С. Лейбензона. Л.С. Лейбензон указал замечательное сходство уравнения (5.21) с дифференциальным уравнением неустановившегося движения газа в пористой среде. В дальнейшем мы рассмотрим эту аналогию.