2. Прогнозирование на основе тренда временного ряда

Построим таблицу исходных данных (таблица 4).

Таблица 4 – Ежедневный оборот магазина «Ткани для дома» в условных единицах

t	yt
1	11,4
2	12,6
3	13,0
4	12,4
5	13,9
6	13,4
7	14,8
8	13,6
9	15,2
10	14,5
11	17,4
12	15,7
78	167,9

По исходным данным построим график динамики изменения ежедневного оборота магазина «Ткани для дома» (рисунок 2).

Рисунок 2 – Ежедневный оборот магазина «Ткани для дома» в условных

единицах

На основе визуального анализа можно предположить, что во временном ряду имеет место тенденция в виде возрастающего тренда и дисперсии.

Ряд имеет сильную колеблемость, поэтому осуществим сглаживание исходных данных методом скользящей средней с шагом сглаживания, равным 3. Для этого рассчитаем среднюю по каждым 3 уровням временного ряда по формуле (7):

(7)

Результаты расчёта представим в таблице 5.

Таблица 5 – Расчёт сглаженных значений по исходным данным

t	yt	уt сгл.
1	11,4	–
2	12,6	12,3
3	13,0	12,7
4	12,4	13,1
5	13,9	13,2
6	13,4	14,0
7	14,8	13,9
8	13,6	14,5
9	15,2	14,4
10	14,5	15,7
11	17,4	15,9
12	15,7	–
78	167,9	–

На основе визуального анализа сглаженного временного ряда с относительно высокой степенью вероятности можно сделать вывод: во временном ряду имеет место тенденция линейного тренда и дисперсии.

Метод Фостера – Стюарта позволяет выявить с определённой вероятностью наличие в ряде тренда и тенденции дисперсии. Для этого рассчитывается 2 переменные: u_t и l_t, причём:

1) u_t = 1, если у_t > (у_t-1, у_t-2, …, у₁), в противном случае u_t = 0;

2) l_t = 1, если у_t < (у_t-1, у_t-2, …, у₁), в противном случае l_t = 0.

Затем на основе этих величин определяются величины S и D по формулам (8) и (9):

S = ∑St; St = ut + lt;	(8)
D = ∑Dt; Dt = ut – lt.	(9)

Результаты расчёта этих данных представлены в таблице 6.

Таблица 6 – Расчёт показателей по методу Фостера – Стюарта

t	yt	ut	lt	St	Dt
1	11,4	–	–	–	–
2	12,6	1	0	1	1
3	13,0	1	0	1	1
4	12,4	0	0	0	0
5	13,9	1	0	1	1
6	13,4	0	0	0	0
7	14,8	1	0	1	1
8	13,6	0	0	0	0
9	15,2	1	0	1	1
10	14,5	0	0	0	0
11	17,4	1	0	1	1
12	15,7	0	0	0	0
78	167,9	–	–	6	6

Величина S используется для оценки наличия в ряде тенденции дисперсии, а величина D – для оценки наличия в ряде тенденции среднего уровня ряда.

После расчёта S и D выдвинем нулевую гипотезу Н₀: во временном ряде отсутствуют тенденции среднего уровня ряда и дисперсии. Для проверки выдвинутой гипотезы рассчитываются следующие случайные величины по формулам (10) и (11):

;	(10)
,	(11)

где

μ – математическое ожидание величины S;

σ₁ – среднеквадратическая ошибка величины S;

σ₂ – среднеквадратическая ошибка величины D.

По условиям задачи n = 12. В таблице даны значения μ, σ₁, σ₂ только для n = 10 и n = 15. В таком случае используются формулы (12) и (13):

	(12)
	(13)

Расчёт:

μ = 3,858 + 0,311 = 4,169

σ₁ = 1,288 + 0,093 = 1,381

σ₂ = 1,964 + 0,076 = 2,040

Случайные величины t₁ и t₂ имеют распределение Стьюдента с k = n – 1 степенями свободы и заданным уровнем значимости а (как правило, а = 0,001; 0,01; чаще всего используется а = 0,05). Затем определяется доверительная вероятность γ = 1 – а. Затем определяется табличное значение t_γ(k, γ). Полученное табличное значение сравнивается с расчётными t₁ и t₂. Если │t₁│>│t_γ│, то нулевая гипотеза об отсутствии в ряде тенденции дисперсии отклоняется, если │t₁│≤│t_γ│, то нулевая гипотеза принимается. Если │t₂│>│t_γ│, то нулевая гипотеза об отсутствии в ряде тенденции среднего уровня ряда отклоняется, если │t₂│≤│t_γ│, то нулевая гипотеза принимается.

Число степеней свободы k = 12 – 1 = 11. Зададим уровень значимости а = 0,05. Доверительная вероятность γ = 1 – а = 0,95 (95%). Тогда t_γ = 2,201.

По расчёту t₁ = 1,326, следовательно, выполняется условие │t₁│≤│t_γ│. Это означает, что с вероятностью 95% в ряде отсутствует тенденция среднего уровня ряда.

По расчёту t₂ = 2,941, следовательно, выполняется условие │t₂│>│t_γ│. Это с вероятностью 95% говорит о наличии в ряде тенденции дисперсии.

Рассчитаем значение коэффициента Кендела для более точного определения наличия в ряде тенденции среднего уровня ряда. Для этого внесём в таблицу значения количества превышения уровня ряда над всеми предыдущими (таблица 7).

Таблица 7 – Расчёт значений p_t

t	yt	pt
1	11,4	–
2	12,6	1
3	13,0	2
4	12,4	1
5	13,9	4
6	13,4	4
7	14,8	6
8	13,6	5
9	15,2	8
10	14,5	7
11	17,4	10
12	15,7	10
78	167,9	58

Расчётное значение коэффициента Кендела вычисляется по формуле (1):

Дисперсия вычисляется по формуле (2):

Предположим, что с вероятностью t во временном ряде нет тренда. В этом случае должно выполняться соотношение (3).

Выберем вероятность, равную 95%. Тогда коэффициент доверия равен: t = 1,96.

–0,433 < 0,758 < 0,433

Неравенство не выполняется, т.к. τ_р ≥ 0,433. Таким образом, с вероятностью 95% в ряде имеет место возрастающая тенденция среднего уровня ряда.

На основе ранее полученных частных выводов можно сделать обобщенный вывод: с вероятностью 95% во временном ряду имеет место тенденция среднего уровня ряда и тенденция дисперсии. С учетом полученного обобщенного вывода можно считать, что временной ряд является нестационарным процессом.

Рассчитаем параметры линейного тренда методом усреднения левой и правой половины ряда. Для этого условно разобьём таблицу исходных данных на 2 приблизительно равные части (таблица 8).

Таблица 8 – Исходные данные к заданию 2

t	1	2	3	4	5	6	7	8	9	10	11	12
yt	11,4	12,6	13,0	12,4	13,9	13,4	14,8	13,6	15,2	14,5	17,4	15,7

По каждой половине рассчитываются средние значения t и y_t:

1-я половина:

2-я половина:

В результате расчёта получаем 2 точки: А (3,5; 12,8) и Б (9,5; 15,2­). Затем построим график исходного ряда (рисунок 3). На этом графике отложим точки А и Б, через эти две точки до пересечения с осью ординат построим прямую. Пересечение этой прямой с осью у даёт значение а₀.

Рисунок 3 – График временного ряда по исходным данным

Из рисунка 3 получаем а₀ = 11,4.

Для того чтобы найти а₁, используются координаты любой из точек А или Б. Расчёт ведётся по формулам (14) и (15):

(14)

Откуда:

(15)

Расчёт:

Таким образом, уравнение линейного тренда будет иметь вид:

Рассчитаем параметры линейного тренда с помощью метода наименьших квадратов (МНК). Для этого составим систему нормальных уравнений (16):

(16)

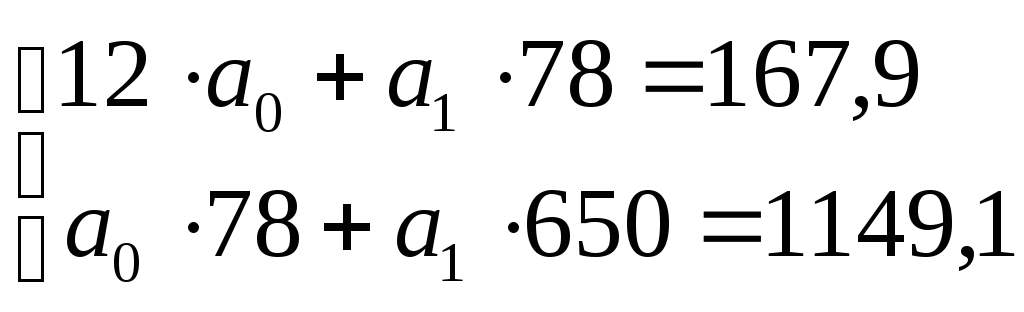
Из этой системы выразим параметры а₀ и а₁ методом определителя по формулам (17) и (18):

	(17)
	(18)

Для расчёта параметров вычислим необходимые суммы показателей. Результаты расчёта представим в таблице 9.

Таблица 9 – Расчёт показателей для вычисления параметров линейного тренда

t	yt	t2	t * y
1	11,4	1	11,4
2	12,6	4	25,2
3	13,0	9	39,0
4	12,4	16	49,6
5	13,9	25	69,5
6	13,4	36	80,4
7	14,8	49	103,6
8	13,6	64	108,8
9	15,2	81	136,8
10	14,5	100	145,0
11	17,4	121	191,4
12	15,7	144	188,4
78	167,9	650	1149,1

Таким образом, уравнение линейного тренда примет вид:

По этому уравнению рассчитаем значения тренда ŷ_t, занесём их в таблицу 10 и построим график (рисунок 4).

Таблица 10 – Расчёт значений линейного тренда

t	yt	ŷt
1	11,4	11,8
2	12,6	12,2
3	13,0	12,6
4	12,4	13,0
5	13,9	13,4
6	13,4	13,8
7	14,8	14,2
8	13,6	14,6
9	15,2	15,0
10	14,5	15,4
11	17,4	15,8
12	15,7	16,2
78	167,9	168

Рисунок 4 – График линейного тренда

Как видно из рисунка 4, тренд, рассчитанный по методу наименьших квадратов, является возрастающим, следовательно, выводы, сделанные нами ранее, подтвердились.

Параметры, рассчитанные по графическому методу, очень близки по значению к рассчитанным по методу наименьших квадратов. Это означает, что график построен правильно.

Предположим, что линейный тренд даёт неточную оценку исходного ряда. Для проверки этого предположения выберем тип нелинейного тренда, который может описать тенденцию исходного временного ряда.

Поскольку после проведения сглаживания ряд всё равно имеет сильную колеблемость, повторим процедуру и получим значения у_{t сгл. 2}. Внесём эти значения в таблицу 11.

Таблица 11 – Расчёт новых сглаженных значений по исходным данным

t	yt	уt сгл.	уt сгл. 2
1	11,4	–	–
2	12,6	12,3	–
3	13,0	12,7	12,7
4	12,4	13,1	13,0
5	13,9	13,2	13,4
6	13,4	14,0	13,7
7	14,8	13,9	14,1
8	13,6	14,5	14,3
9	15,2	14,4	14,9
10	14,5	15,7	15,3
11	17,4	15,9	–
12	15,7	–	–
78	167,9	–	–

Рассчитаем разности первого порядка и темпы роста для новых сглаженных значений по формулам (19) и (20) соответственно:

Δt1 = уt – уt-1	(19)
	(20)

Результаты расчётов приведены в таблице 12.

Таблица 12 – Расчёт разностей первого и второго порядка и темпов роста для новых сглаженных значений

t	yt	уt сгл. 2	Δt1сгл.	Δt2сгл.	Тр t сгл.
1	11,4	–	–	–	–
2	12,6	–	–	–	–
3	13,0	12,7	–	–	–
4	12,4	13,0	0,3	–	1,024
5	13,9	13,4	0,4	0,1	1,033
6	13,4	13,7	0,3	–0,1	1,020
7	14,8	14,1	0,4	0,1	1,032
8	13,6	14,3	0,2	–0,2	1,009
9	15,2	14,9	0,6	0,4	1,042
10	14,5	15,3	0,4	–0,2	1,031
11	17,4	–	–	–	–
12	15,7	–	–	–	–
78	167,9	–	–	–	–

Предварительным условием выбора параболы для описания исходных данных является относительное постоянство разностей второго порядка по абсолютной величине. Они определяются следующим образом (21):

Δt2 = Δt1 – Δt-11

(21)

Результаты расчёта разностей второго порядка приведены в таблице 12 Как видно из таблицы 12, разности второго порядка колеблются в интервале от –0,2 до 0,4. Это, предположительно, говорит о том, что парабола может дать менее точную оценку, чем линейный тренд.

Степенной тренд используется тогда, когда цепные темпы роста экономического показателя, в среднем, либо постепенно возрастают, либо постепенно убывают.

Как видно из таблицы 12, темпы роста колеблются, следовательно, степенной тренд не подходит для описания тенденции данного временного ряда.

Показательный (экспоненциальный) тренд используется при условии, когда экономический показатель имеет относительно постоянный цепной темп роста, который в среднем равен а₁. Цепной темп роста определяется по формуле (20).

Как видно из таблицы 12, цепные темпы роста изменяются в интервале от 1,009 до 1,042, следовательно, данный тип тренда, возможно, может дать более точную оценку.

Исходя из сущности гиперболы (наличия предела, к которой она приближается с ростом фактора − времени), она может быть использована, если экономический показатель, изменяясь во времени, приближается к определенному пределу.

Поскольку функция возрастающая, то её значение стремится к бесконечности, поэтому гипербола также даст неточную оценку.

Рассчитаем параметры для экспоненциального тренда. Уравнение тренда имеет вид (22):

(22)

Для того чтобы составить систему нормальных уравнений, необходимо привести уравнение тренда в линейный вид при помощи логарифмирования:

Система нормальных уравнений будет иметь вид (23):

(23)

Для расчёта параметров вычислим необходимые суммы показателей. Результаты расчёта представим в таблице 13.

Таблица 13 – Расчёт показателей для вычисления параметров экспоненциального тренда

t	yt	lnyt	t * lnyt
1	2	3	4
1	11,4	2,43361	2,43361
2	12,6	2,53370	5,06739
3	13,0	2,56495	7,69485
4	12,4	2,51770	10,07079
5	13,9	2,63189	13,15944
6	13,4	2,59525	15,57153
7	14,8	2,69463	18,86239
8	13,6	2,61007	20,88056

окончание таблицы 13

1	2	3	4
9	15,2	2,72130	24,49166
10	14,5	2,67415	26,74149
11	17,4	2,85647	31,42117
12	15,7	2,75366	33,04393
78	167,9	31,58737	209,43881

Далее выразим параметры lna₀ и lna₁ методом определителя по формулам (24) и (25):

	(24)
	(25)

Для нахождения величин a₀ и a₁ проведём потенцирование, в результате которого получим а₀ = 11,53; а₁ = 1,03.

Уравнение тренда примет вид:

Аппроксимация (приближение) − это замена исходных данных наиболее близкими к ним другими данными, представленными в виде тренда.

Для выбора трендовой модели, которая наилучшим образом аппроксимировала бы исходные данные, используются различные критерии, например, критерий наименьшей суммы квадратов отклонений.

Если сравниваются трендовые модели, у которых одинаковое число параметров, то критерий наименьшей суммы квадратов отклонений будет иметь следующий вид (26):

S = ∑(yt – ŷt)2 → min

(26)

Вычислим значения ŷ_t для линейного и экспоненциального тренда: ŷ_{t л} и ŷ_{t э}, рассчитаем квадрат их отклонения от фактических значений y_t и внесём результаты расчётов в таблицу 14.

Таблица 14 – Расчёт квадратов отклонений линейного и экспоненциального трендов от фактических значений

t	yt	ŷt л	(yt – ŷt л)2	ŷt э	(yt – ŷt э)2
1	11,4	11,8	0,16	11,876	0,226
2	12,6	12,2	0,16	12,232	0,135
3	13,0	12,6	0,16	12,599	0,161
4	12,4	13,0	0,36	12,977	0,333
5	13,9	13,4	0,25	13,366	0,285
6	13,4	13,8	0,16	13,767	0,135
7	14,8	14,2	0,36	14,180	0,384
8	13,6	14,6	1,00	14,606	1,012
9	15,2	15,0	0,04	15,044	0,024
10	14,5	15,4	0,81	15,495	0,991
11	17,4	15,8	2,56	15,960	2,073
12	15,7	16,2	0,25	16,439	0,546
78	167,9	–	6,27	–	6,305

Рассчитав суммы квадратов отклонений аппроксимированных значений от фактических, можно сделать вывод, что линейный тренд даёт более точную оценку, так как сумма квадратов отклонений значений линейного тренда меньше, чем экспоненциального. Однако можно сказать, что эти виды трендов дают приблизительно одинаковые оценки, так как значения квадратов отклонений отличаются на малую величину.

Построим график исходного ряда и два типа рассчитанных трендов (рисунок 5).

Рисунок 5 – Сравнение линейного и экспоненциального трендов

Как видно из рисунка 5, вначале тренды совпадают, а к концу ряда несколько расходятся, но в целом дают приблизительно одинаковую оценку.

После определения параметров тренда и выбора с позиции аппроксимации наилучшей трендовой модели необходимо оценить адекватность выбранной модели исходным данным.

Любой временной ряд можно представить по формуле (27):

уt = trt + st + ct + εt

(27)

Но, поскольку временные ряды по факту достаточно короткие, то значения сезонной и циклической составляющих могут быть неявно выражены, поэтому временной ряд можно выразить по формуле (28):

уt = trt + εt

(28)

Из этого выражения найдём случайную составляющую (29):

εt = уt – trt

(29)

Если вместо теоретического значения тренда tr_t подставить выбранный тренд, то найдём величину e_t по формуле (30):

еt = уt – ŷt

(30)

Результаты расчётов приведены в таблице 15.

Таблица 15 – Расчёт величины e_t

t	yt	ŷt л	et
1	11,4	11,8	–0,4
2	12,6	12,2	0,4
3	13,0	12,6	0,4
4	12,4	13,0	–0,6
5	13,9	13,4	0,5
6	13,4	13,8	–0,4
7	14,8	14,2	0,6
8	13,6	14,6	–1,0
9	15,2	15,0	0,2
10	14,5	15,4	–0,9
11	17,4	15,8	1,6
12	15,7	16,2	–0,5
78	167,9	168	–0,1

Если доказать, что величина е_t является случайной, то это будет означать, что выбранный тренд ŷ_t соответствует теоретическому tr_t. Для этого используются 4 условия.

I. Колебания величины е_t носят случайный характер.

Чтобы проверить условие 1, используется критерий поворотных точек. Величина е_t будет являться поворотной (р_t), если выполняется одно из двух неравенств (31) и (32):

еt-1 < еt > еt+1	(31)
еt-1 > еt < еt+1	(32)

Если выполняется одно из этих условий, то величине p_t присвоим значение 1.

Значения величины p_t приведены в таблице 16.

Таблица 16 – Расчёт величины p_t

t	yt	et	pt
1	2	3	4
1	11,4	–0,4	–
2	12,6	0,4	0
3	13,0	0,4	0
4	12,4	–0,6	1
5	13,9	0,5	1
6	13,4	–0,4	1

окончание таблицы 16

1	2	3	4
7	14,8	0,6	1
8	13,6	–1,0	1
9	15,2	0,2	1
10	14,5	–0,9	1
11	17,4	1,6	1
12	15,7	–0,5	–
78	167,9	–0,1	8

Для понимания этих условий строится график (рисунок 6).

Рисунок 6 – График величины e_t

Выдвинем нулевую гипотезу: колебания величины е_t носят случайный характер. Для проверки гипотезы рассмотрим теоретические значения поворотных точек – математическое ожидание и дисперсию величины p по формулам (33) и (34) соответственно:

	(33)
	(34)

Сопоставим расчётное значение числа поворотных точек с его теоретическими значениями (35):

,

(35)

где t – коэффициент доверия, равный 1 при выбранной вероятности 68,3% или 1,96 при вероятности 95%.

Если выполняется данное неравенство, то с выбранной вероятностью колебания величины е_t носят случайный характер.

Примем вероятность 95%. Тогда t = 1,96.

4,03 < 8 < 9,31

Неравенство выполняется, следовательно, с вероятностью 95% колебания величины e_t носят случайный характер.

II. Распределение величины e_t соответствует нормальному распределению. Для проверки условия используется RS-критерий, рассчитываемый по формуле (36):

,

(36)

где S_ŷ – среднеквадратическое отклонение, рассчитывается по формуле (37):

,

(37)

n – количество уровней ряда;

m – число параметров трендовой модели.

Для расчёта среднеквадратического отклонения вычислим необходимые данные e_t² и занесём их в таблицу 17.

Таблица 17 – Расчёт величины e_t²

t	yt	et	et2
1	2	3	4
1	11,4	–0,4	0,16
2	12,6	0,4	0,16
3	13,0	0,4	0,16
4	12,4	–0,6	0,36

окончание таблицы 17

1	2	3	4
5	13,9	0,5	0,25
6	13,4	–0,4	0,16
7	14,8	0,6	0,36
8	13,6	–1,0	1,00
9	15,2	0,2	0,04
10	14,5	–0,9	0,81
11	17,4	1,6	2,56
12	15,7	–0,5	0,25
78	167,9	–0,1	6,27

Для нахождения расчётного значения RS-критерия используется таблица значений RS-критерия для n = 10…30.

В таблице приводятся нижнее и верхнее значения RS-критерия для n = 10 и n = 20; а у нас n = 12. Для нахождения нижнего и верхнего значений RS-критерия для n = 12 используем линейную интерполяцию, аналогично формулам (12) и (13):

RS_{12 ниж} = 2,67 + 0,102 = 2,772

RS_{12 верх} = 3,85 + 0,128 = 3,978

Для проверки условия 2 выдвигается нулевая гипотеза: распределение величины е_t соответствует нормальному. При этом должно выполняться неравенство (38):

RSn ниж. < RSр < RSn верх.,

(38)

где RS_{n ниж.} и RS_{n верх.} – соответственно нижнее и верхнее значения RS-критерия.

Если это условие выполняется, то с выбранной вероятностью распределение величины е_t соответствует нормальному.

2,772 < 3,283 < 3,978

Неравенство выполняется, следовательно, с вероятностью 95% распределение величины e_t соответствует нормальному распределению.

III. Математическое ожидание величины е_t равно 0: М(е_t) = 0. Для проверки этого условия выдвинем нулевую гипотезу: М(е_t) = 0. Для проверки гипотезы определяется расчётное значение t_р по формуле (39):

,

(39)

где

е_ср – среднее арифметическое значение величины е_t;

S_e – среднеквадратическое значение величины е_t, вычисляемое по формуле (40):

(40)

Для расчёта среднеквадратического значения вычислим необходимые данные (e_t – е_ср)² и занесём их в таблицу 18.

Таблица 18 – Расчёт величины (e_t – е_ср)²

t	yt	et	(et – еср)2
1	2	3	4
1	11,4	–0,4	0,153
2	12,6	0,4	0,167
3	13,0	0,4	0,167
4	12,4	–0,6	0,350
5	13,9	0,5	0,258
6	13,4	–0,4	0,153
7	14,8	0,6	0,370
8	13,6	–1,0	0,983
9	15,2	0,2	0,043
10	14,5	–0,9	0,795

окончание таблицы 18

1	2	3	4
11	17,4	1,6	2,587
12	15,7	–0,5	0,242
78	167,9	–0,1	6,269

Затем находим табличное значение t_Т, которое зависит от числа степеней свободы k и доверительной вероятности γ. Зная k и γ, по таблице значений t-критерия Стьюдента найдём значение t_Т, которое соответствует распределению Стьюдента.

Число степеней свободы k = 12 – 1 = 11. Зададим уровень доверительной вероятности γ = 0,95 (95%). Тогда t_γ = 2,201.

Сопоставим теоретическое и табличное значения t. Если │t_р│<│t_Т│, то с выбранной вероятностью нулевая гипотеза принимается.

│–0,038│<│2,201│, следовательно, с вероятностью 95%, математическое ожидание величины e_t равно 0.

IV. Независимость уровней ряда по отношению друг к другу. Если уровни ряда независимы друг от друга, то в ряде отсутствует автокорреляция. Для оценки наличия тенденции автокорреляции необходимо использовать критерий Дарбина – Уотсона, который рассчитывается по формуле (41):

(41)

Для расчёта критерия вычислим необходимые данные (e_t – е_t-1)² и занесём их в таблицу 19.

Таблица 19 – Расчёт величины (e_t – е_t-1)²

t	yt	et	(et – еt-1)2
1	11,4	–0,4	–
2	12,6	0,4	0,64
3	13,0	0,4	0,00
4	12,4	–0,6	1,00
5	13,9	0,5	1,21
6	13,4	–0,4	0,81
7	14,8	0,6	1,00
8	13,6	–1,0	2,56
9	15,2	0,2	1,44
10	14,5	–0,9	1,21
11	17,4	1,6	6,25
12	15,7	–0,5	4,41
78	167,9	–0,1	20,53

Критерий Дарбина – Уотсона изменяется в пределах [0; 4]. Если d_р > 2, то это означает, что он находится в отрицательной области, но, поскольку все исходные табличные значения рассчитаны для положительной области, то в этом случае расчётное значение коэффициента Дарбина – Уотсона пересчитывается по формуле (42):

dр` = 4 – dр

(42)

d_р` = 4 – 3,274 = 0,726

Затем, на следующем этапе определяется табличные значения коэффициента: d₁ и d₂. Для его нахождения необходимо предварительно определить число уровней ряда n и число факторов v. При n = 12 и v = 1 табличные значения d₁ = 0,97; d₂ = 1,33.

На последнем этапе сопоставляется расчётное и теоретическое значения коэффициента.

1. Если d_р < d₁, то в ряде есть автокорреляция.

2. Если d_р > d₂, то в ряде нет автокорреляции.

3. Если d₁ ≤ d_р ≤ d₂, то необходимо провести дополнительные расчёты с помощью коэффициента автокорреляции.

В данной задаче выполняется условие d_р < d₁, то есть 0,726 < 0,97. Это означает, что в ряде присутствует автокорреляция.

Чтобы исключить влияние автокорреляции, рассчитаем значения e`_t для сглаженных уровней ряда. Данные представим в таблице 20.

Таблица 20 – Расчёт новых значений e`_t

t	уt сгл.	ŷt	e`t	e`t2	(e`t – e`t-1)2
1	–	11,8	–	–	–
2	12,3	12,2	0,1	0,01	–
3	12,7	12,6	0,1	0,01	0,00
4	13,1	13,0	0,1	0,01	0,00
5	13,2	13,4	–0,2	0,04	0,09
6	14,0	13,8	0,2	0,04	0,16
7	13,9	14,2	–0,3	0,09	0,25
8	14,5	14,6	–0,1	0,01	0,04
9	14,4	15,0	–0,6	0,36	0,25
10	15,7	15,4	0,3	0,09	0,81
11	15,9	15,8	0,1	0,01	0,04
12	–	16,2	–	–	–
78	–	168	–0,3	0,67	1,64

Рассчитаем новый коэффициент Дарбина – Уотсона по формулам (41) и (42):

d_р` = 4 – 2,448 = 1,552

Теперь выполняется условие d_р > d₂, то есть 1,552 > 1,33. Это означает, что автокорреляция в ряде отсутствует.

Таким образом, величина е_t является случайной. Это означает, что выбранный линейный тренд ŷ_t с вероятностью 95% соответствует теоретическому tr_t.

Рассчитаем точечный и интервальный прогнозы развития оборота магазина «Ткани для дома».

Точечный прогноз определяется по формуле (4):

Интервальный прогноз вычисляется по формуле (5). Для расчёта дисперсии вычислим значения (y_t – у_ср)². Результаты расчёта представим в таблице 21.

Таблица 21 – Вычисление значений (y_t – y_ср)² по исходным данным

t	yt	(yt – уср)	(yt – уср)2
1	11,4	–2,6	6,76
2	12,6	–1,4	1,96
3	13,0	–1,0	1,00
4	12,4	–1,6	2,56
5	13,9	–0,1	0,01
6	13,4	–0,6	0,36
7	14,8	0,8	0,64
8	13,6	–0,4	0,16
9	15,2	1,2	1,44
10	14,5	0,5	0,25
11	17,4	3,4	11,56
12	15,7	1,7	2,89
78	167,9	–	29,59

Число степеней свободы равно k = 12 – 1 = 11. Выберем уровень значимости а = 0,05. Тогда доверительная вероятность составит γ = 1 – а = 0,95 (95%). При k = 11, γ = 95% табличное значение t_γ = 2,201.

Интервальный прогноз:

Таким образом, с вероятностью 95%, на 13-й день оборот магазина «Ткани для дома» будет лежать в интервале:

12,95 < ỹ_t < 15,03