8. Похибки функцій

Поряд з наведеними вище правилами обчислення похибок деяких дій над наближеними числами можна записати аналогічні правила і для обчислення значень функцій, аргументами яких є наближені числа. Найбільш повним є загальне правило, засноване на обчисленні приросту (похибки) функції при заданих приростах (похибках) аргументів.

Розглянемо функцію однієї змінної . Нехай – наближене значення аргументу , – його абсолютна похибка. Абсолютну похибку функції можна вважати її приростом, який вона набуває при зміні аргументу на . З курсу математичного аналізу відомо (), що цей приріст можна замінити диференціалом:

.

Тоді для абсолютної похибки функції отримаємо вираз:

.

Аналогічний вираз можна записати для функції декількох змінних. Так, для абсолютної похибки функції , наближені значення аргументів якої відповідно, абсолютна похибка має вигляд:

, (4)

де ,, – абсолютні похибки аргументів.

Формула (4) називається загальною формулою похибок.

Відносна похибка знаходиться за формулою:

. (5)

Отримані співвідношення можна використовувати для виведення похибок довільної функції. Зокрема, таким способом легко отримати вирази правил 1-3 обчислення похибок.

Приклад 6. Обчислити і визначити похибки результату, використовуючи загальну формулу похибок:

,

де , , .

Розв’язання. Обчислимо (див. Приклад 5.)

.

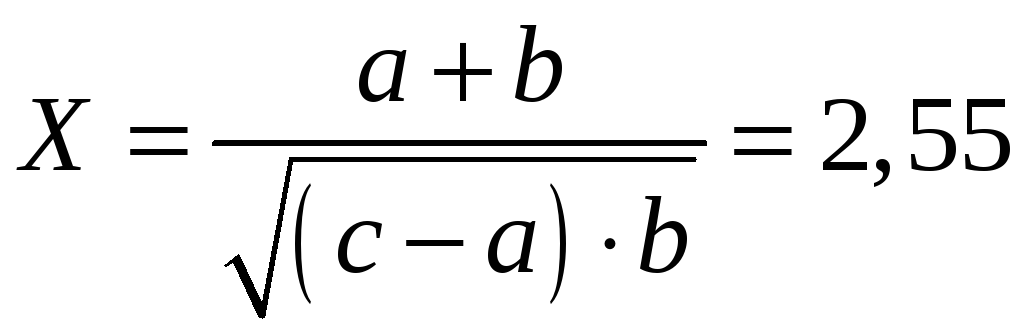За загальною формулою похибок:

.

.

9. Правила підрахунку цифр

Точний підрахунок похибок результатів обчислень наближених чисел досить громіздкий. Тому здебільшого на практиці користуються наступними правилами підрахунку цифр:

1. При додаванні і відніманні наближених чисел молодший збережений розряд результату має бути найбільшим серед розрядів, що виражаються останніми значущими цифрами вихідних даних.

2. При множенні і діленні наближених чисел у результаті потрібно зберегти стільки значущих цифр, скільки їх має наближене дане з найменшою кількістю значущих цифр.

3. При піднесенні до квадрата або до куба в результаті потрібно зберегти стільки значущих цифр, скільки їх має число, яке підносять до степеня.

4. При добуванні кореня в результаті потрібно брати стільки значущих цифр, скільки їх у підкореневому виразі.

5. При обчисленні проміжних результатів потрібно брати на одну-дві цифри більше, ніж рекомендують попередні правила.

6. Якщо дані можна брати з довільною точністю, то, щоб знайти результат з правильними цифрами, дані потрібно брати з такою кількістю цифр, яка забезпечує правильну цифру в результаті, відповідно до правил 1-4.

Приклад. Обчислити, користуючись правилами підрахування цифр:

, де , .

Розв’язання. Маємо:

.

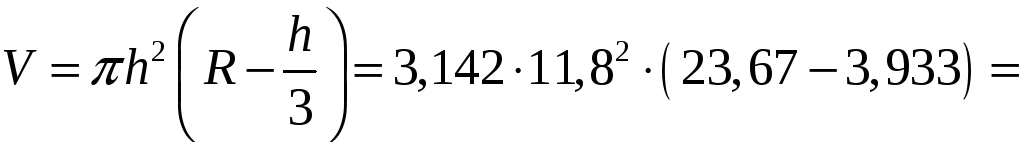
Відповідь: .

10. Коректність та обумовленість задачі

Розглянемо питання коректності задачі. Більшість задач, які доводиться розв’язувати, можна записати у вигляді , де – деяка відома величина, – шукана величина, – задана функція (оператор). Величини і можуть бути числами, масивами чисел, функціями однієї чи багатьох змінних тощо.

Задача називається коректно поставленою, якщо для будь-яких вихідних даних з деякого класу розв’язок існує, єдиний і стійкий за вхідними даними.

Стійка за вхідними даними та задача, розв’язок якої неперервно залежить від вхідних даних, тобто для таких задач , коли . Якщо ця умова не виконується, то задача називається нестійкою за вхідними даними. У цьому випадку навіть незначна похибка у вхідних даних може викликати як завгодно великі похибки в розв’язку, тобто розв’язок може бути зовсім спотворений. Прикладом некоректної задачі є задача диференціювання.

Якщо для похибок розв’язку і вхідних даних існує співвідношення

,

де – досить велика константа, то задача формально стійка, але неусувна похибка в цьому випадку може бути значною. Це випадок так званої слабкої стійкості (слабкої обумовленості). Параметр називають числом обумовленості задачі. Очевидно, що чим більше значення , тим гірше обумовлене завдання. Класичним прикладом погано обумовленої задачі є знаходження кореня полінома високого порядку.

Із слабкою обумовленістю ми зустрінемося, наприклад, при розв’язуванні систем лінійних алгебраїчних рівнянь, визначник яких близький до нуля. Для таких систем похибки в коефіцієнтах системи або похибки округлення при розрахунках можуть призвести до результату, далекого від шуканого розв’язку.