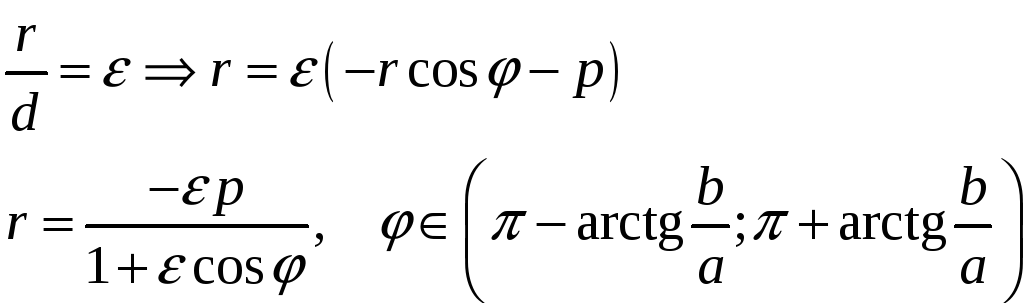- •Определение 4
- •Теорема 2
- •Теорема 5
- •Теорема 6
- •Теорема 7
- •Теорема 8
- •Определение 19
- •Теорема 9
- •Теорема 13 (о базисе в пространстве, на плоскости, на прямой)
- •Теорема 14
- •Теорема 18 (критерий коллинеарности)
- •Определение 39
- •Теорема 19 (критерий компланарности)
- •Определители Определение 40
- •Преобразование аффинной системы координат на плоскости
- •Определение 50
- •Различные способы задания прямой на плоскости
- •1) Нахождение угла между прямыми
- •2) Расстояние от точки до прямой
- •Плоскость в пространстве Определение 51
- •Теорема 23
- •Способы задания плоскости в пространстве
- •Определение 52
- •Прямая в пространстве
- •Определение 53
- •Определение 54
- •Определение 55
- •Кривые второго порядка Эллипс Определение 56
- •Определение 57
- •Определение 58
- •Свойства эллипса
- •Определение 59
- •Определение 60
- •Определение 61
- •Эксцентриситет и директриса
- •Определение 62
- •Определение 63
- •Уравнение эллипса в полярных координатах
- •Гипербола Определение 64
- •Определение 65
- •Свойства гиперболы
- •Определение 66
- •Определение 67
- •Определение 68
- •Полярное уравнение гиперболы
- •Парабола Определение 69
- •1 Случай
- •2 Случай
- •Теорема 25
- •Теорема 26
- •Цилиндрические поверхности Определение 79
- •Конические поверхности Определение 80
- •Определение 81
Определение 65
Уравнение вида
 ,
где
,
где
![]() называется каноническим уравнением
гиперболы, а система координат, в которой
гипербола имеет каноническое уравнение
называется канонической системой
координат.
называется каноническим уравнением
гиперболы, а система координат, в которой
гипербола имеет каноническое уравнение
называется канонической системой
координат.
Свойства гиперболы
Пусть в канонической
системе координат гипербола имеет
уравнение
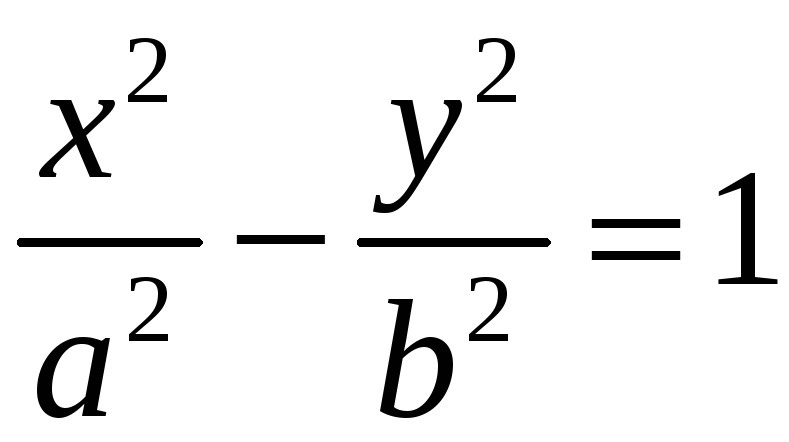 .
.
1) Гипербола обладает
двумя осями симметрии (главные оси).
Одна ось симметрии – ось
![]() ,
другая – ось
,
другая – ось
![]() .
Одна из осей симметрии – фокальная ось
(ось, проходящая через фокусы).
.
Одна из осей симметрии – фокальная ось
(ось, проходящая через фокусы).
2) Точка пересечения осей симметрии является точкой симметрии гиперболы.
3) Из уравнения
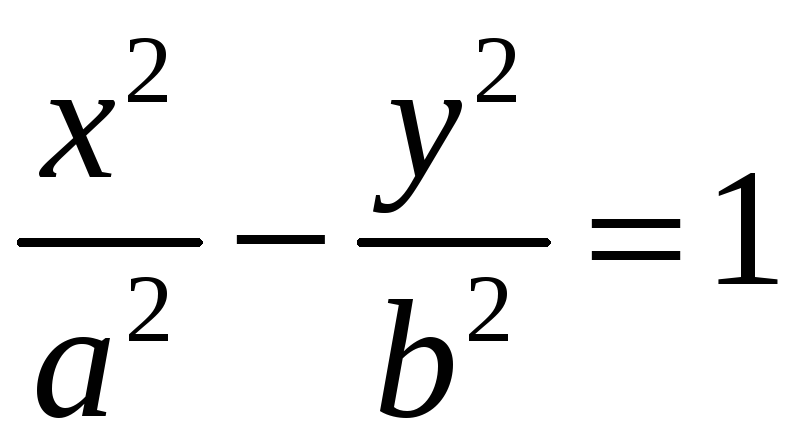 получаем, что в полосе
получаем, что в полосе
![]() точек гиперболы нет.
точек гиперболы нет.
4) Из уравнения
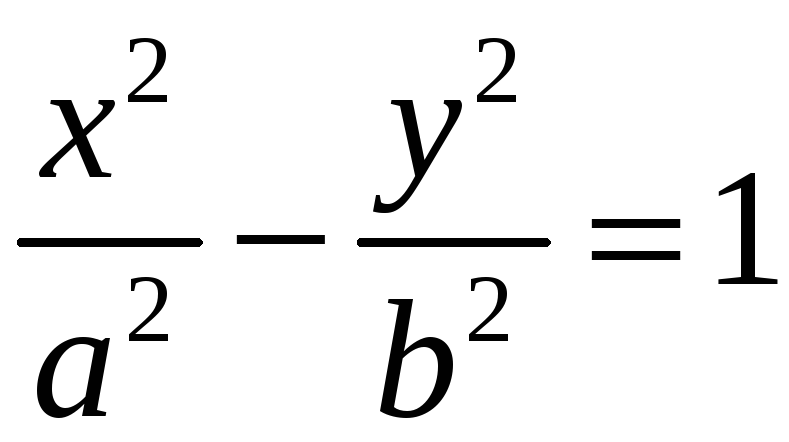 следует, что
следует, что
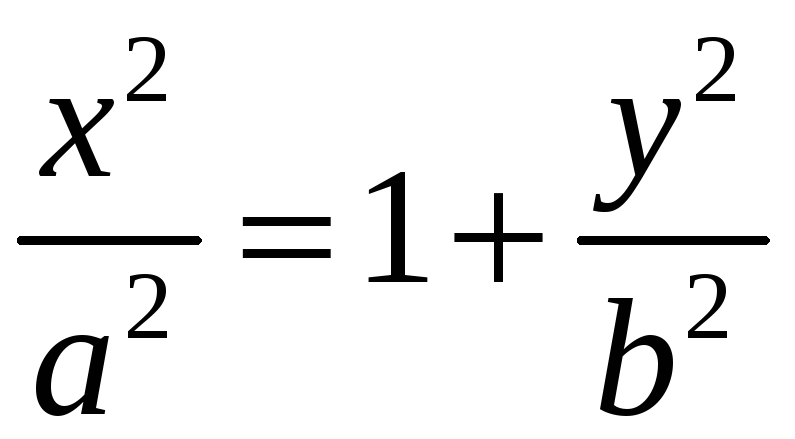 ,
т.е.
,
т.е.
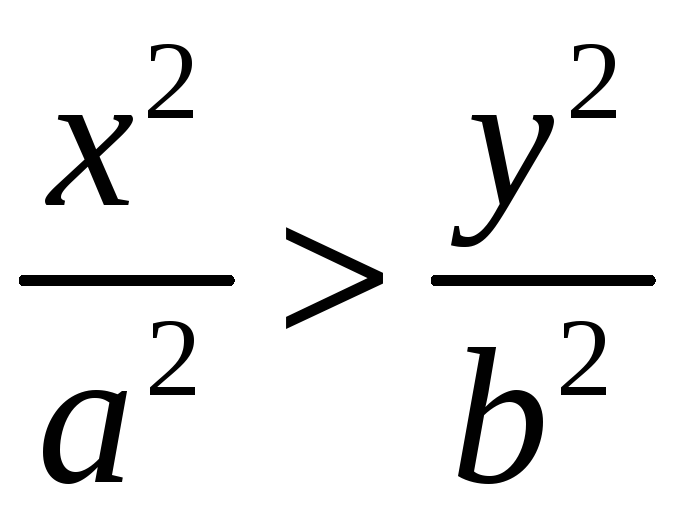 .
Значит гипербола лежит между прямыми
.
Значит гипербола лежит между прямыми
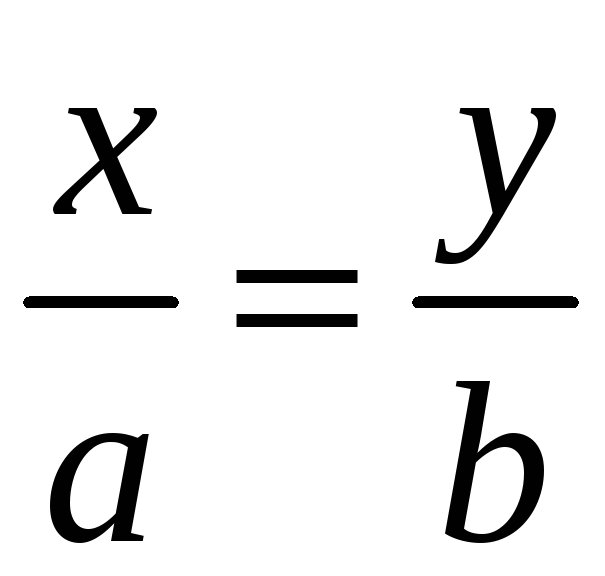 и
и
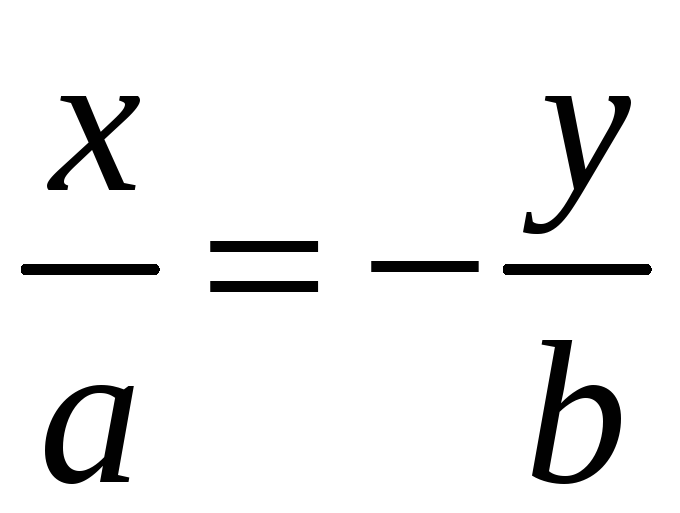 ,
как показано на рисунке:
,
как показано на рисунке:
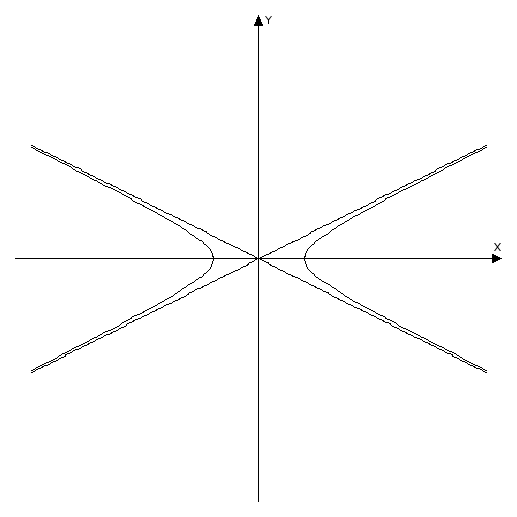
Определение 66
Точки пересечения фокальной оси с гиперболой называются вершинами гиперболы.
Прямые
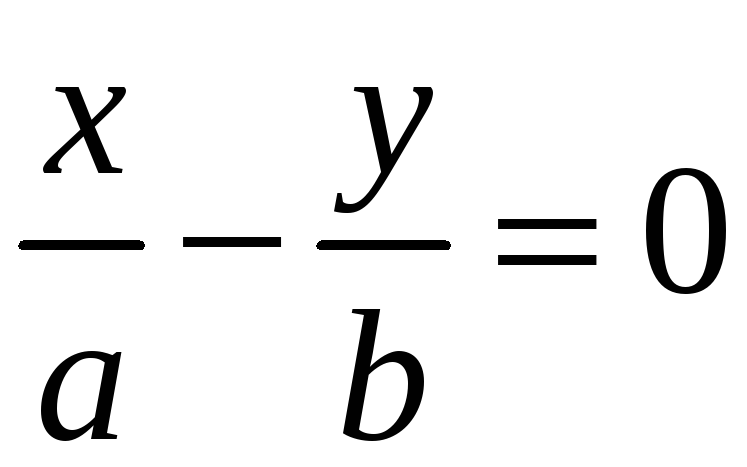 и
и
 являются асимптотами гиперболы.
являются асимптотами гиперболы.
Рассмотрим прямую
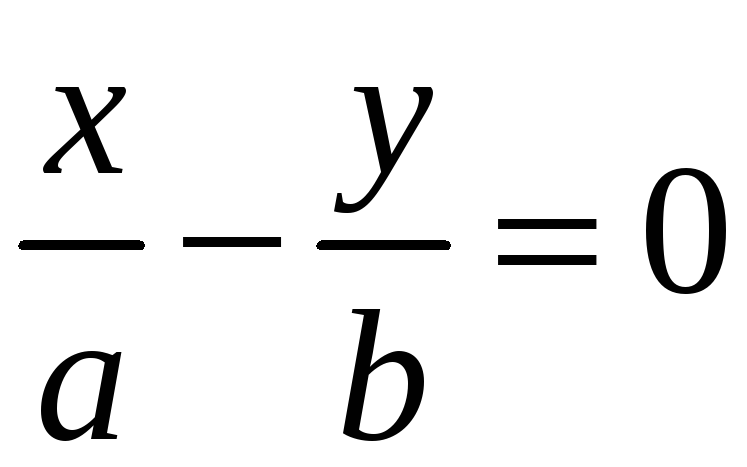 и часть гиперболы
и часть гиперболы
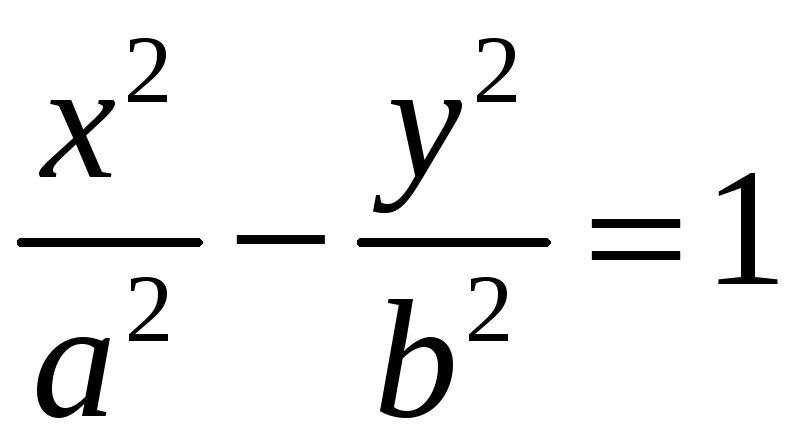 ,
где
,
где
![]() .
Тогда
для прямой
.
Тогда
для прямой
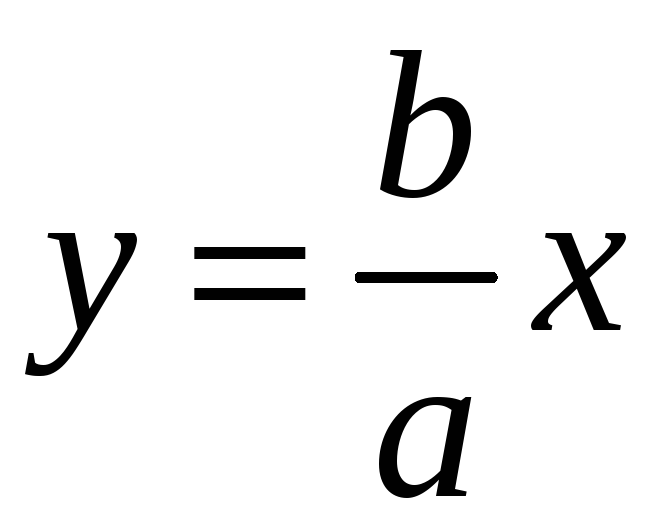 ,
для гиперболы
,
для гиперболы
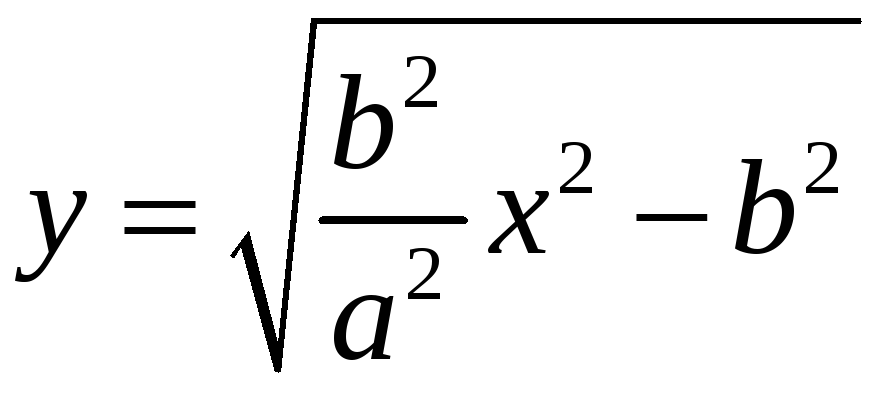
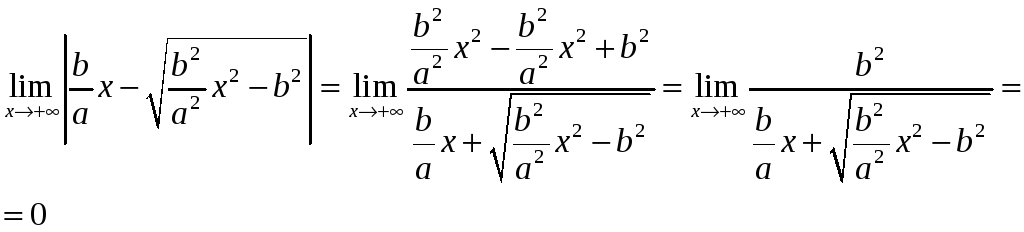
Аналогично для
остальных частей гиперболы (![]() )
и прямой
)
и прямой
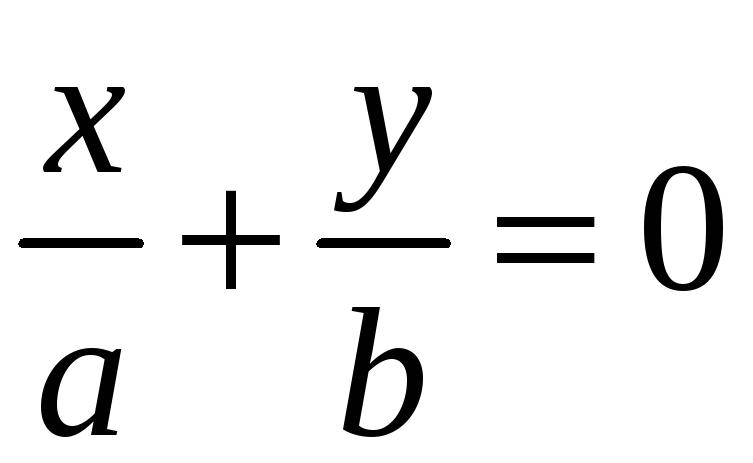 .
.
Определение 67
Число
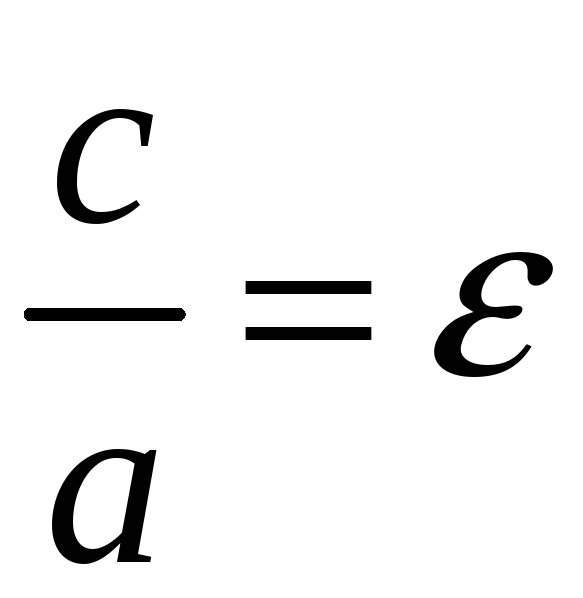 называется эксцентриситетом гиперболы.
Так как
называется эксцентриситетом гиперболы.
Так как
![]() ,
то
,
то
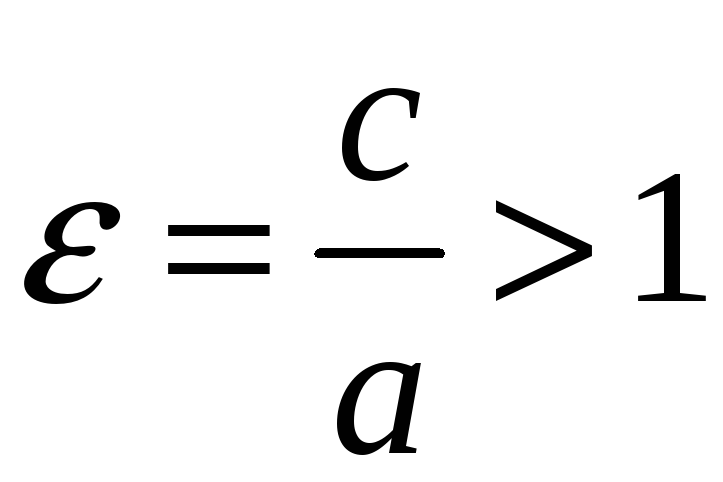 .
.
Рассмотрим прямую
![]() ,
где
,
где
![]() Расстояние от точки
Расстояние от точки
![]() до этой прямой равно
до этой прямой равно
![]() .
Расстояние от точки
.
Расстояние от точки
![]() до фокуса
до фокуса
![]() равно
равно
![]() и до точек гиперболы
и до точек гиперболы
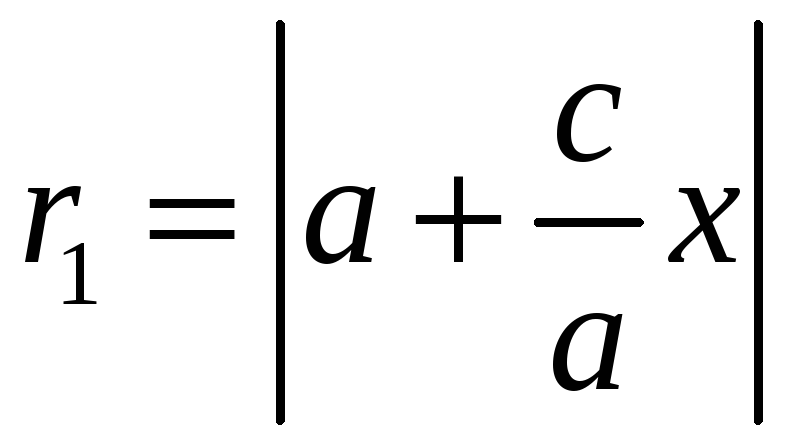 .
Отношение расстояния от точки гиперболы
до фокуса и до прямой
.
Отношение расстояния от точки гиперболы
до фокуса и до прямой
![]() равно
равно
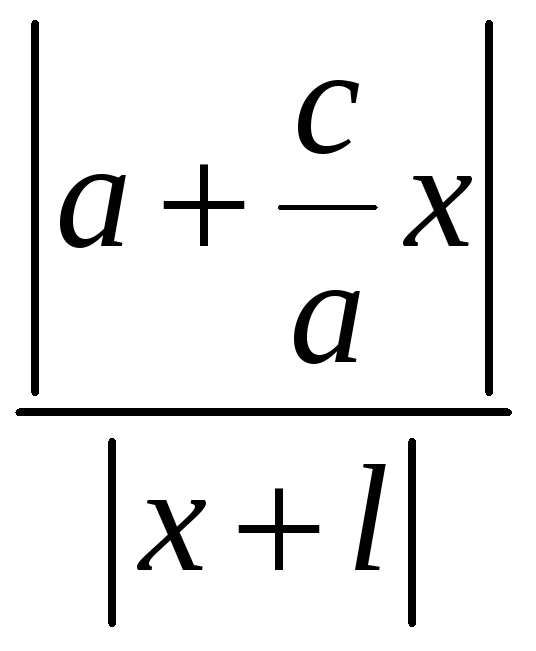 .
Это отношение постоянно, когда
.
Это отношение постоянно, когда
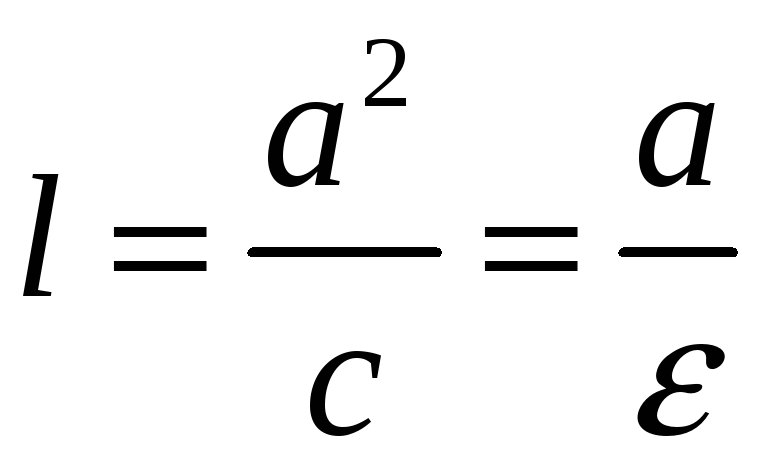 .
Таким образом отношение расстояний от
точек гиперболы до фокуса
.
Таким образом отношение расстояний от
точек гиперболы до фокуса
![]() и от точек гиперболы до прямой
и от точек гиперболы до прямой
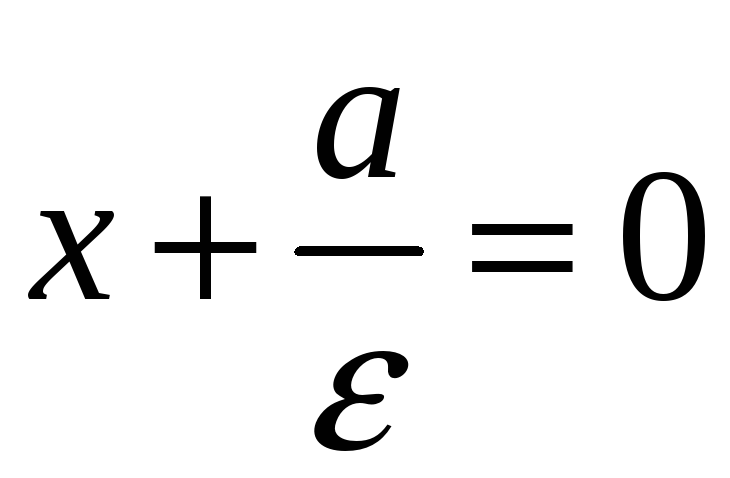 постоянно и равно
постоянно и равно
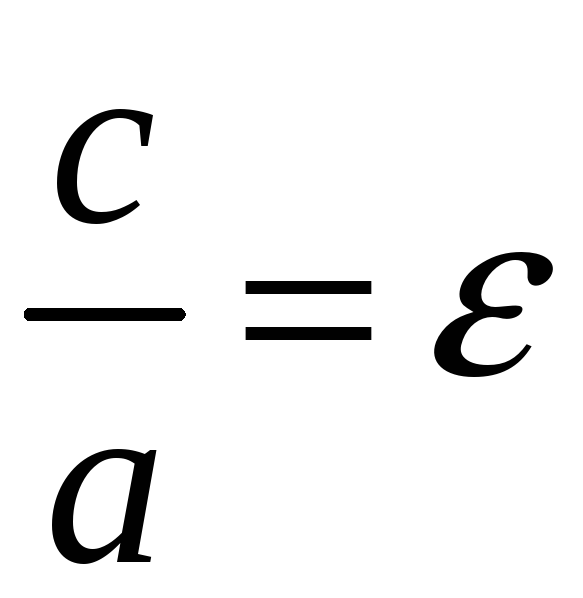 .
.
Определение 68
Прямая, перпендикулярная
фокальной оси, пересекающая отрезок
между фокусами
![]() и
и
![]() ,
отстоящая от фокуса
,
отстоящая от фокуса
![]() на расстояние
на расстояние
![]() называется директрисой гиперболы для
фокуса
называется директрисой гиперболы для
фокуса
![]() .
Директриса фокуса
.
Директриса фокуса
![]() в канонической системе координат имеет
уравнение
в канонической системе координат имеет
уравнение
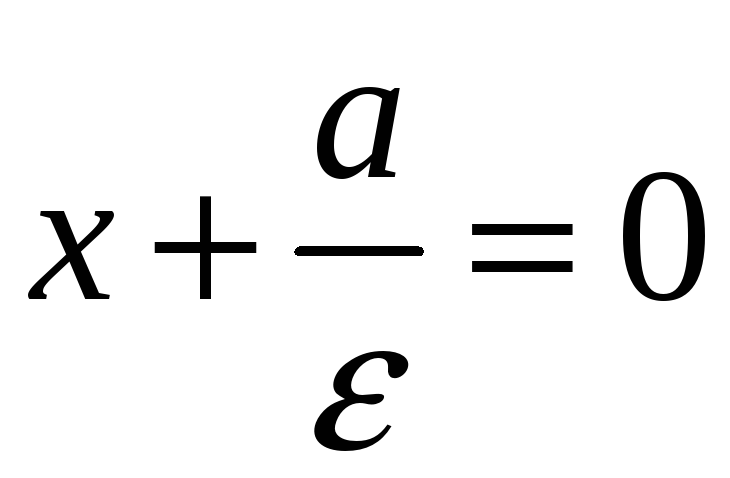 .
Директриса фокуса
.
Директриса фокуса
![]() в канонической системе координат имеет
уравнение
в канонической системе координат имеет
уравнение
 .
.
Проверим, что
точка, для которой отношение расстояний
до фокуса и до директрисы этого фокуса
равно
![]() принадлежит гиперболе.
принадлежит гиперболе.
Пусть точка имеет
координаты
![]() .
Расстояние до фокуса
.
Расстояние до фокуса
![]() равно
равно
![]() .
Расстояние до директрисы
.
Расстояние до директрисы
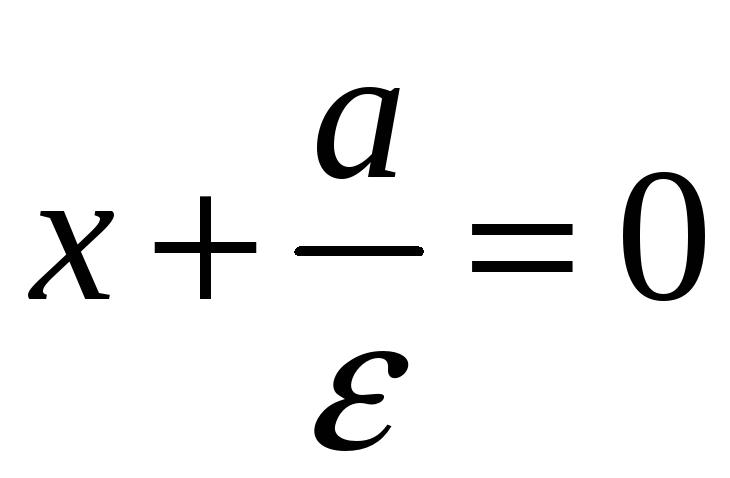 равно
равно
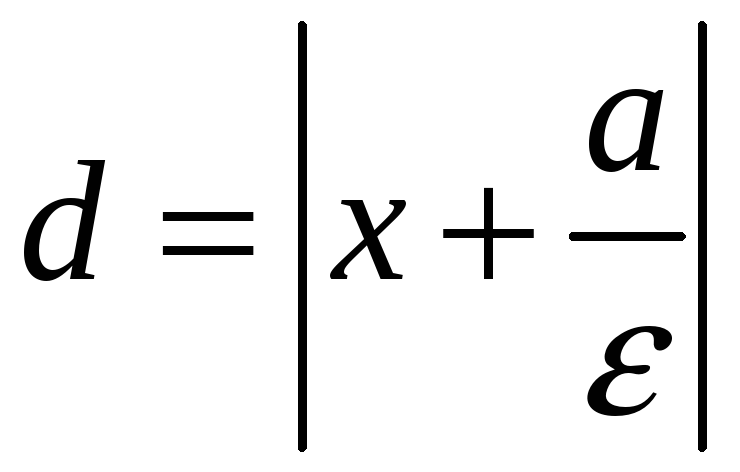 .
Так как
.
Так как
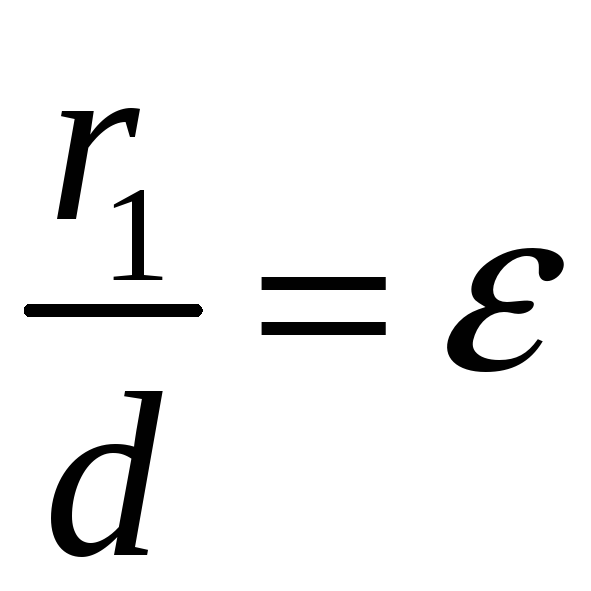 ,
то
,
то
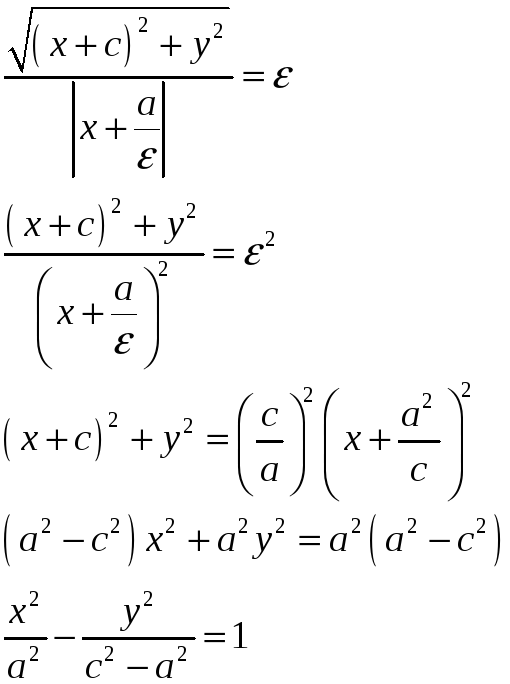
Получили, что точка
![]() принадлежит гиперболе. Аналогично
доказывается для второго фокуса.
принадлежит гиперболе. Аналогично
доказывается для второго фокуса.
Пусть задана прямая
![]() ,
точка
,
точка
![]() и
и
![]() .
Тогда найдется гипербола, для которой
точка
.
Тогда найдется гипербола, для которой
точка
![]() является фокусом, а прямая
является фокусом, а прямая
![]() директрисой относительно этого фокуса,
директрисой относительно этого фокуса,
![]() является эксцентриситетом гиперболы.
Построим гиперболу. Для этого выберем
систему координат. Ось
является эксцентриситетом гиперболы.
Построим гиперболу. Для этого выберем
систему координат. Ось
![]() проведем через
проведем через
![]() перпендикулярно прямой
перпендикулярно прямой
![]() .
Точку пересечения оси
.
Точку пересечения оси
![]() и прямой
и прямой
![]() обозначим через
обозначим через
![]() .
Возьмем точку
.
Возьмем точку
![]() на отрезке
на отрезке
![]() так, чтобы
так, чтобы
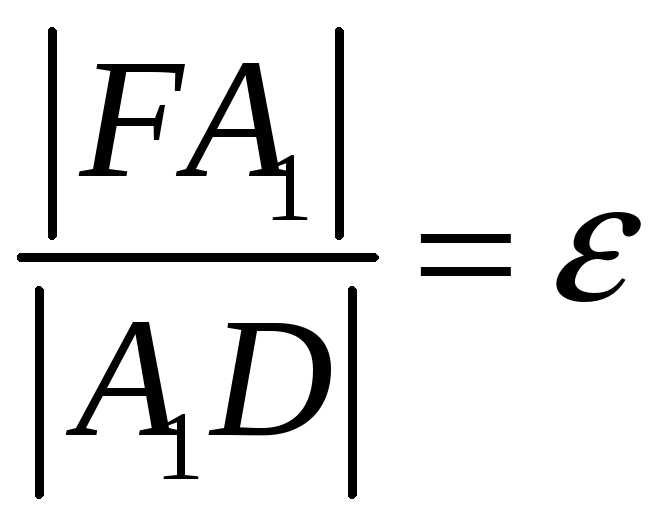 и точку
и точку
![]() на оси
на оси
![]() такую,
что
такую,
что
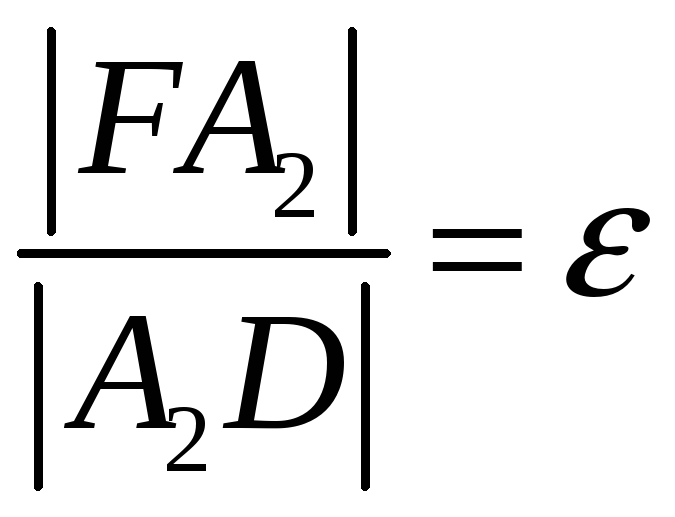 .
Точка
.
Точка
![]() лежит по другую сторону от
лежит по другую сторону от
![]() ,
чем точка
,
чем точка
![]() .
Выберем началом системы координат
середину отрезка
.
Выберем началом системы координат
середину отрезка
![]() .
Обозначим начало координат
.
Обозначим начало координат
![]() .
Очевидно, что точка
.
Очевидно, что точка
![]() лежит
по одну сторону от прямой
лежит
по одну сторону от прямой
![]() ,
что и точка
,
что и точка
![]() (так как
(так как
![]() ).
Обозначим
).
Обозначим
![]() ,
,
![]() .
Направление оси
.
Направление оси
![]() выберем так, чтобы точка
выберем так, чтобы точка
![]() имели координаты
имели координаты
![]() .
.
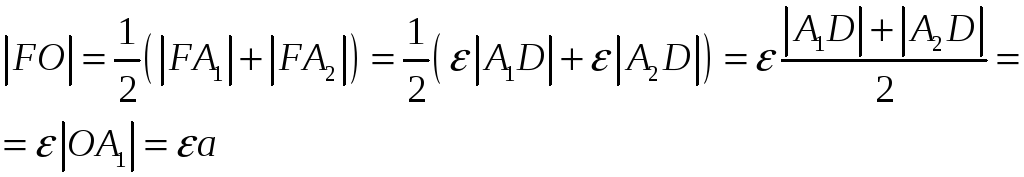
Получили, что
![]() или
или
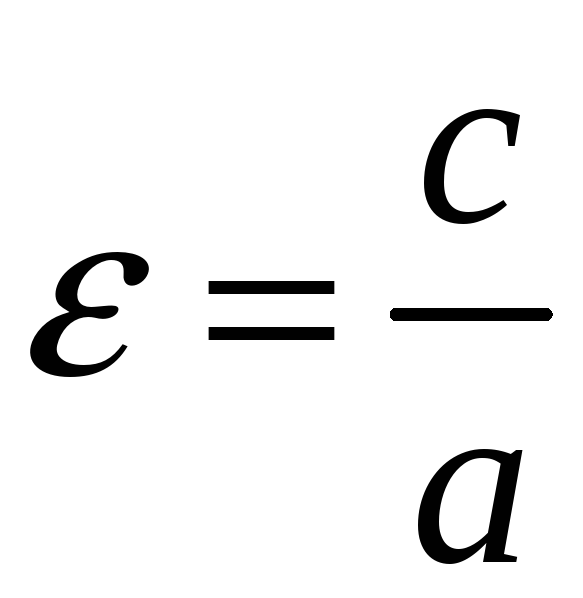 .
Найдем
.
Найдем
![]() :
:
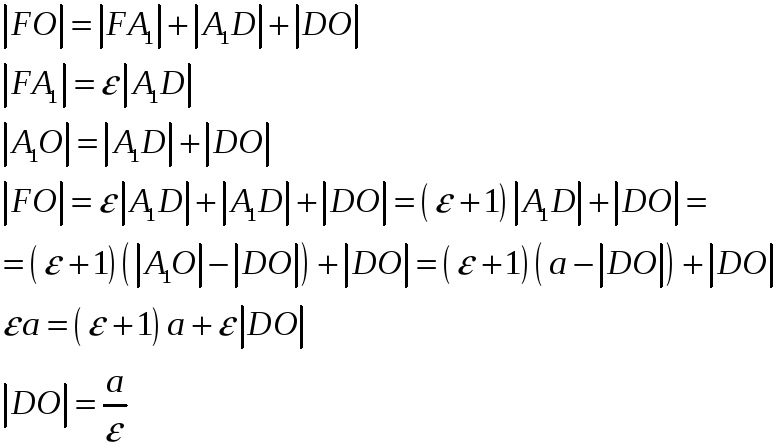
Получили, что
уравнение прямой
![]() имеет вид
имеет вид
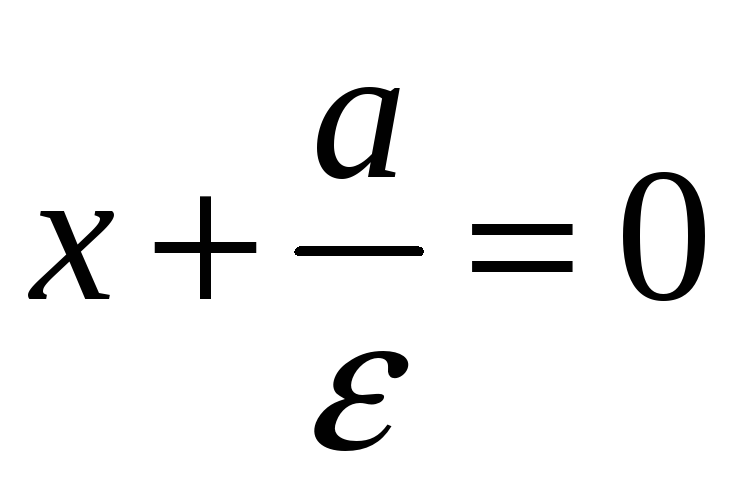 .
Для гиперболы
.
Для гиперболы
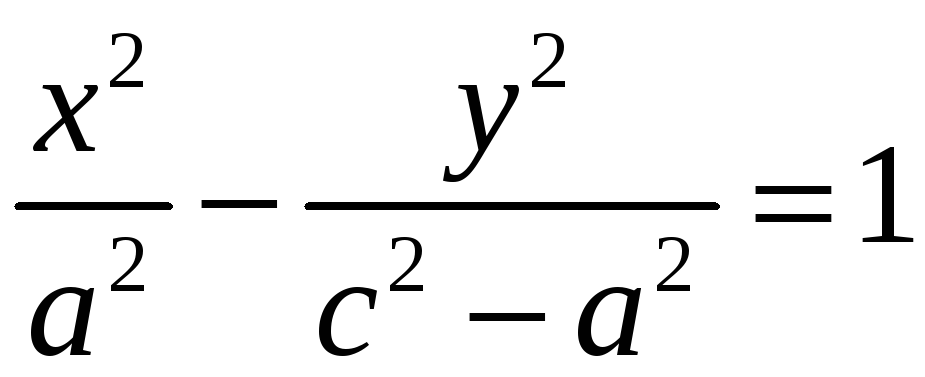 точка
точка
![]() является фокусом, а прямая
является фокусом, а прямая
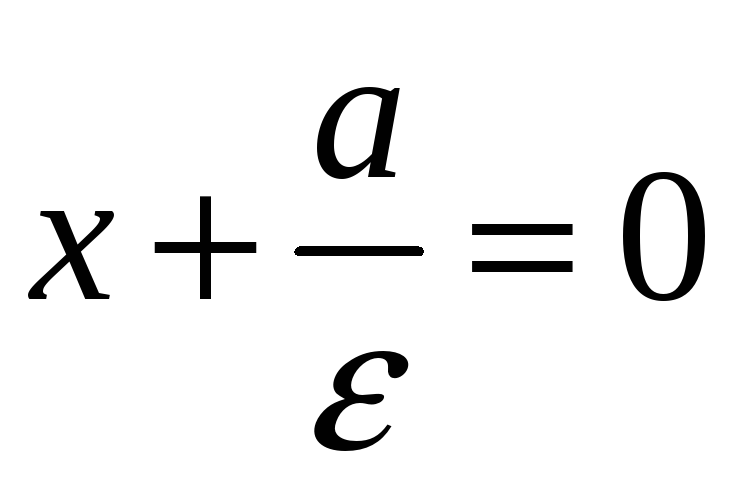 является директрисой, соответствующей
этому фокусу.
является директрисой, соответствующей
этому фокусу.
Полярное уравнение гиперболы
Пусть в канонической
системе координат уравнение гиперболы
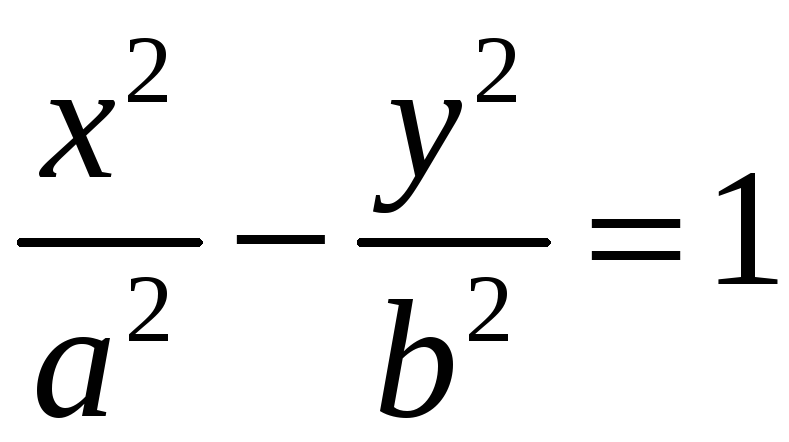 .
Введем систему координат так: началом
системы координат является точка
.
Введем систему координат так: началом
системы координат является точка
![]() ,
а полярной осью является ось
,
а полярной осью является ось
![]() ,
где
,
где
![]() .
Тогда для правой ветви гиперболы имеем:
если точка
.
Тогда для правой ветви гиперболы имеем:
если точка
![]() принадлежит правой ветви гиперболы, то
расстояние от
принадлежит правой ветви гиперболы, то
расстояние от
![]() до директрисы
до директрисы
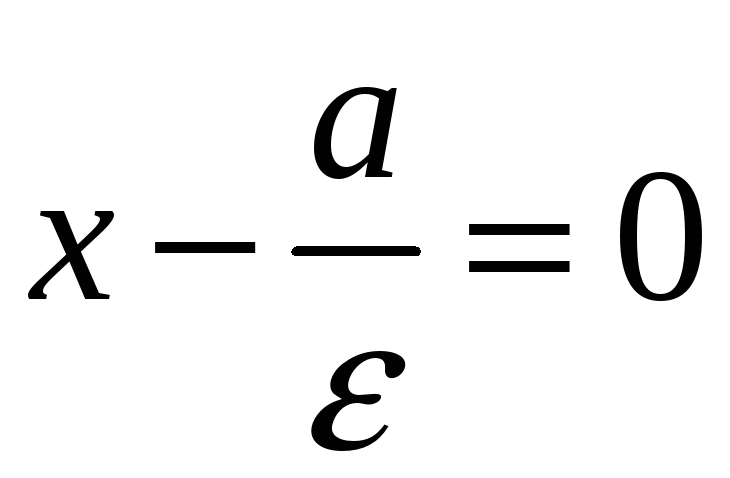 равно расстоянию от фокуса до директрисы
плюс
равно расстоянию от фокуса до директрисы
плюс
![]() .
Обозначим расстояние от фокуса до
директрисы через
.
Обозначим расстояние от фокуса до
директрисы через
![]() .
Тогда
.
Тогда
![]()
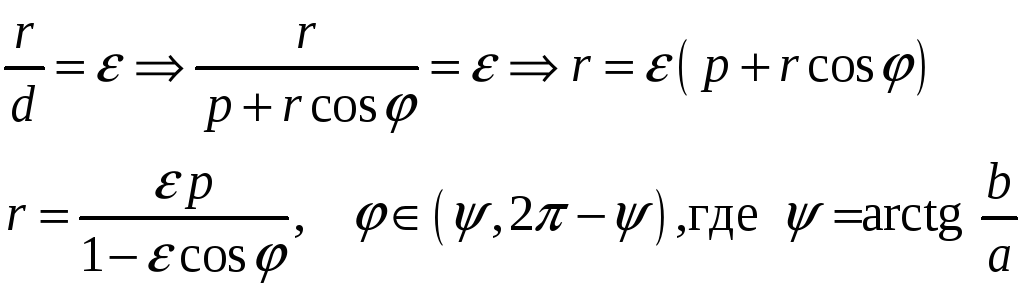
Если
![]() принадлежит левой ветви гиперболы, то
расстояние от точки
принадлежит левой ветви гиперболы, то
расстояние от точки
![]() до директрисы равно
до директрисы равно
![]() .
.