
- •Скоробогатова т.Н. ____________ «_____»____________2001г.
- •Балаково 20001 содержание
- •Введение
- •1 Описание схемотехнического решения
- •Функциональная схема системы автоматического управления технологическим процессом электрохимических ванн
- •2 Выбор элементов локальной системы автоматики и расчет их передаточных функций
- •2.1 Выбор микропроцессора
- •2.2 Выбор насоса
- •2.3 Выбор двигателя
- •2.4. Выбор концентратомера
- •5 Построение желаемых лачх и фчх. Анализ желаемой фчх.
5 Построение желаемых лачх и фчх. Анализ желаемой фчх.
Для построения желаемых ЛАЧХ и ФЧХ необходимо знать временные показатели качества переходного процесса: время регулирования tр, перерегулирование и колебательность М.
Построим переходный процесс, методом обратного преобразования Лапласа с помощью программы MathCAD 2000 Professional
![]()

Рисунок 5. Вещественная частотная характеристика передаточной функции

![]()
![]()
![]()
tр


Рисунок 6. Переходный процесс
По графику h(t) найдем показатели качества переходного процесса. [7]
tр – минимальное время, за которое управляемая величина достигает установившего значения hуст(t) с заданной точностью (=5%);
tр=6,88 с.
- максимальное отклонение от установившегося значения hуст(t), выраженное в процентах:
![]() (18)
(18)
Кроме временных показателей качества, о переходном процессе можно судить по частотным характеристикам. Построим АЧХ системы, используя программу MathCAD 2000 Professional
![]()
![]()
![]()
![]()

Рисунок 7. АЧХ системы
Показателем качества в этом случае будет колебательность М, характеризующая склонность системы к колебаниям [7]:
![]() (19)
(19)
Желаемая ЛАЧХ разомкнутой системы строится, исходя из требований, предъявляемых к проектируемой системе и к основным показателям качества переходного процесса.
Основными требованиями к системе считаются: требуемый коэффициент усиления (определяемый желательной точность ее работы), желательный порядок астатизма системы, допустимое время переходного процесса, требуемый запас устойчивости по фазе (определяемый величиной перерегулирования).
Будем строить желаемую ЛАЧХ исследуемой системы, использую метод запретной области. [7]
Рассмотрим низкочастотную часть желаемой ЛАЧХ системы.
Отметим в низкочастотной области желаемой ЛАЧХ запретную зону для обеспечения требований по ошибке при заданных скорости и ускорении входного сигнала.
Запишем некоторые данные из технического задания для нашей системы:
Максимально допустимая ошибка:
![]() , (20)
, (20)
Максимальна скорость изменения концентрации кислоты:
![]() , (21)
, (21)
Максимальное ускорение:
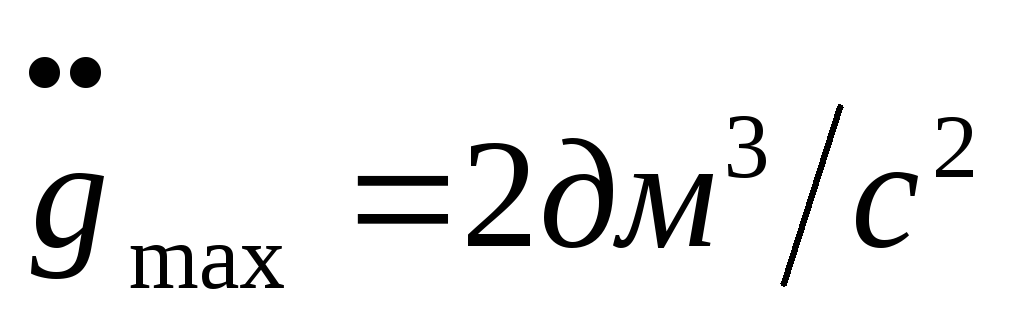 (22)
(22)
Наиболее просто определить точность системы по воспроизведению гармонического входного сигнала с рабочей амплитудой А и частотой контрольной точки k:
![]() (23)
(23)
Найдем первую и вторую производную от выражения
![]() , (24)
, (24)
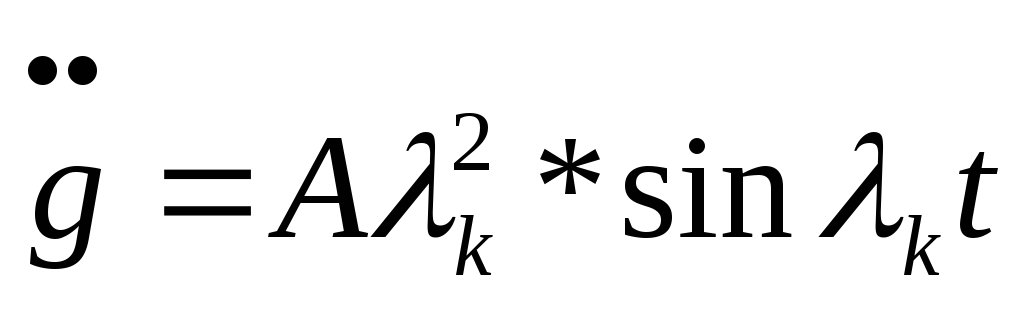 (25)
(25)
В этих уравнениях:
![]() ,
(26)
,
(26)
 (27)
(27)
Разделим (27) на (26)
 ,
(28)
,
(28)
Из уравнения (26)
 (29)
(29)
Подставим числовые значения в выражения (28) и (29):
![]() , (30)
, (30)
![]() .
(31)
.
(31)
Вычислим амплитуду контрольной точки:
![]() ,
(32)
,
(32)
![]() .
(33)
.
(33)
Таким образом, можно сформулировать требования к низкочастотной части желаемой ЛАЧХ системы: для того что бы входное гармоническое воздействие с ошибкой, не превышающей доп, ЛАЧХ системы должна проходить не ниже контрольной точки Ак (15037;-141,1), то есть строим запретную область.
Исследуем среднечастотную область желаемой ЛАЧХ разомкнутой системы. Ранее были определены показатели качества системы:
Перерегулирование =
Время регулирования, характеризующее быстроту затухания переходного процесса tр=6,88 с,
Колебательность М=1.
По номограмме Солодовникова для заданного перерегулирования определим время регулирования tр. По шкале Солодовникова время регулирования заданно функцией частоты среза [7, c.632]:
![]() .
(34)
.
(34)
По этому выражению, с учетом известного времени регулирования, найдем необходимую частоту среза:
![]() .
(35)
.
(35)
Вычислим граничные частоты среднечастотной ЛАЧХ. Для этого нужно определить протяженность h участка среднечастотной ЛАЧХ:
![]() (35)
(35)
Следовательно, граничных частот ЛАЧХ иметь не будет так как целиком состоит из среднечастотной части.
Через найденную точку ср проведем прямую с наклоном –20Дб/дек. На многочисленных примерах подтверждено, что такой наклон обеспечивает необходимые запасы устойчивости.
Таким образом, получим желаемую ЛАЧХ с наклоном –20Дб/дек (рисунок 4 – Lж()).
Построенная желаемая ЛАЧХ лежит выше точки Ак, то есть не попадает в запретную область.
Передаточная функция полученной желаемой ЛАЧХ запишется в виде:
![]() .
(36)
.
(36)
По таблице для типовых динамических звеньев, определяем, что желаемая ЛАЧХ является интегрирующим звеном.
ФЧХ такого звена есть прямая, параллельная оси псевдочастот и проходящая через точку (0; -/2), рисунок 4 ().
По графикам Lж() и () определим, обеспечиваются ли в нашей системе запасы устойчивости по амплитуде и по фазе. Запас по амплитуде определяется на частоте, соответствующей точке пересечения ФЧХ с линией –1800. В данном случае ФЧХ не пересекается с прямой –1800, поэтому запас устойчивости по амплитуде является достаточным. Запас устойчивости по фазе – это превышение (ср) над линией –1800. Из графика видно, что частотная характеристика на частоте ср имеет запас по фазе =900, тогда как достаточным для обеспечения устойчивости системы является =30400.
Таким образом, можно сделать вывод, что при выборе Lж() устойчивость системы обеспечивается.
6. ПОСТРОЕНИЕ ЛАЧХ КОРРЕКТИРУЮЩЕГО УСТРОЙСТВА. ВЫБОР КОРРЕКИРУЮЩЕГО УСТРОЙСТВА УСТАНОВЛЕНИЕ КОРРЕКИРУЮЩЕГО УСТРОЙСТВА В СИСТЕМУ, ОБОСНОВАНИЕ УСТАНОВЛЕНИЯ
Для коррекции системы используется корректирующее устройство последовательного типа, поскольку оно обеспечивает наиболее простую схему включения, не требует сложных элементов для согласования, передает значительные величины управляющих сигналов (тока, напряжения), кроме того расширяет полосу пропускания частот при наличии дифференцирующих звеньев в цепи регулирования [7, с.359], что позволяет передавать большую мощность сигнала.
Как известно, корректирующее устройство можно включать между различными элементами исходной системы. При выборе места включения руководствуются минимумом вносимой устройством погрешности.
Система, в которую необходимо включить корректирующее устройство, состоит из: микропроцессора, двигателя, насоса, концентратомера, емкости и клапана.
Ниже анализируются возможные места включения корректирующего устройства.
Включение электрического корректирующего устройства в виде RC-цепочки между двигателем и насосом не представляется возможным, так как сигнал, снимаемый с двигателя, носит неэлектрический характер. Включение электрического корректирующего устройства между насосом и емкостью, емкостью и клапаном по той же причине не представляется возможным.
Включение корректирующего устройства между концентратомером и собственно микропроцессором усложняет обратную связь системы, что может отрицательно повлиять на быстродействие системы, поэтому такое включение хоть и возможно, но не желательно.
Остается один вариант: между микропроцессором и двигателем. Малое выходное сопротивление порта микропроцессора позволяет легко согласовать его с RC-цепочкой корректирующего звена и практически без потерь передать сигнал. В свою очередь корректирующее устройство соединено с двигателем, что позволяет непосредственно управлять его перемещением. Кроме того, такое включение не усложняет цепь обратной связи, что благоприятно сказывается на быстродействии системы.

1 – микропроцессор;
2 – двигатель;
3 – насос;
4 – концентратомер
5 – емкость
6 – клапан
7 – корректирующее устройство
Рисунок 8. Полученная структурная схема скорректированной системы
ЛАЧХ корректирующего устройства получается при вычитании из желаемой логарифмической характеристики неизменяемой части, рисунок 4:
![]() .
(37)
.
(37)
Из графика видно, что передаточная функция корректирующего устройства имеет вид:
![]() .
(38)
.
(38)
Для нахождения передаточной функции ЛАЧХ корректирующего звена необходимо найти постоянную времени и коэффициент усиления. T1=1c, k=1,58*106. Тогда передаточная функция корректирующего устройства примет вид:
![]() ,
(39)
,
(39)
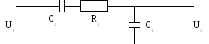
Рисунок 9. Схема корректирующего устройства [7, с.644]
Параметры RC-цепочки рассчитывают по формулам [7, с.644]:
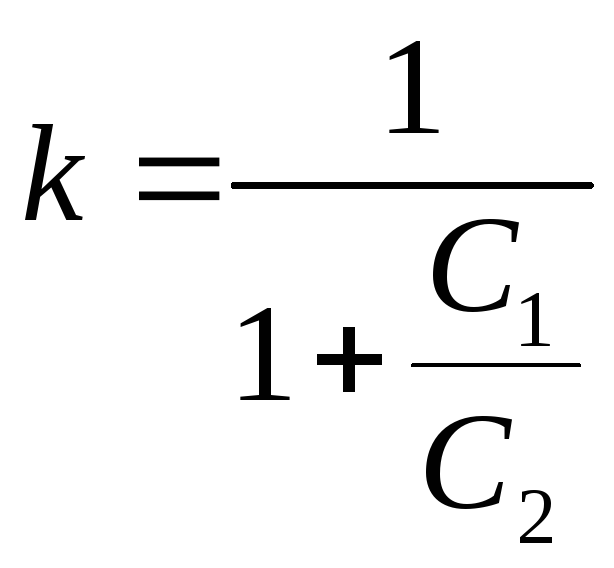 ,
(40)
,
(40)
![]() (41)
(41)
Значение емкости С1 = 10*10-6 Ф. Тогда, с учетом того, что k=1,58*106 по формуле (40) рассчитаем С2 = 10*10-6 Ф.
Подставив в формулу (41) значения C1, C2 T0, рассчитаем значение R = 200000 Ом.
При этом микропроцессор не изымается из системы, так как по-прежнему выполняет роль сравнивающего устройства.
Возможно также корректировать управление работой САУ при помощи программы для микропроцессора, которая будет реализовывать передаточную функцию корректирующего устройства, определенную формулой (38). Для этого требуется найти разностное уравнение в реальном масштабе времени.
Микропроцессор выявляет отклонение полученного сигнала от желаемого, то есть необходимого в данный момент, и выдает команду на устранение этого отклонения.
Значения желаемого сигнала задаются в микропроцессоре в цифровом виде. Вычисления производятся в машинном коде.
Подставим в выражение (38) числовые значения:
![]() .
(42)
.
(42)
Выполним обратное z – преобразование X(z) x(t). Для этого необходимо применить подстановку:
![]() ,
(43)
,
(43)
![]() .
(44)
.
(44)
Перейдем от – преобразования к z – преобразованию, осуществив следующую подстановку:
![]() ,
(45)
,
(45)
 ,
(46)
,
(46)
![]() .
(47)
.
(47)
Итак, W(z) – передаточная функция, равная отношению сигнала управления u(z) к сигналу ошибки e(z):
![]() ,
(48)
,
(48)
![]() .
(49)
.
(49)
Основное выражение z – преобразования:
![]() , (50)
, (50)
где Т0 – период дискретности.
z – преобразование – это преобразование Лапласа от решетчатой функции, для которой характерно выражение nT0=t, где n – число дискретов в конечном промежутке времени t [7]
Из этого соотношения выразим период дискретности:
![]() ,
(51)
,
(51)
![]() .
(52)
.
(52)
Из последнего выражения получим:
![]() .
(53)
.
(53)
Таким образом, выражение (49) можно переписать в виде
![]() ,
(54)
,
(54)
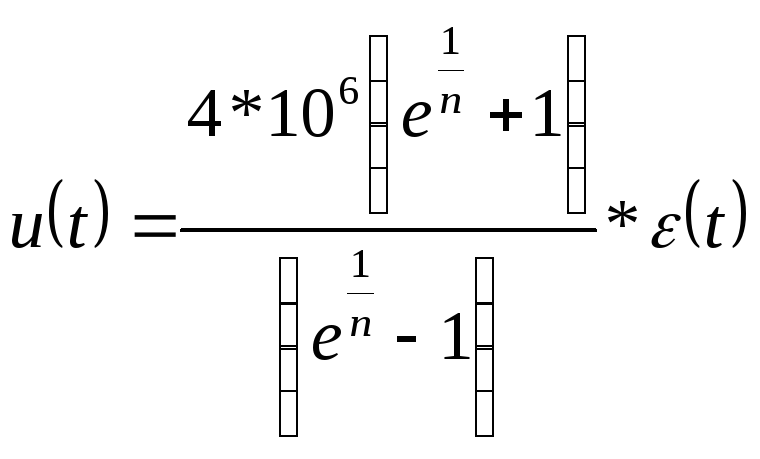 (55)
(55)
Введем обозначение:
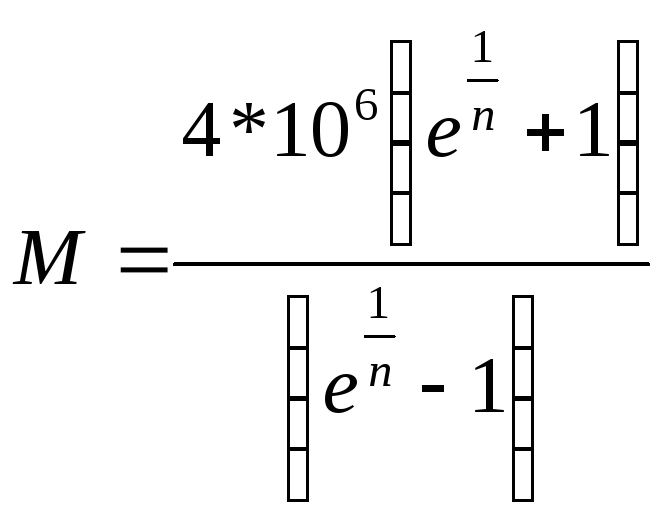 ,
(56)
,
(56)
В результате выражение (55) запишется в виде
![]() .
(57)
.
(57)
Таким образом, мы рассмотрели цифровой фильтр, на вход которого подавался сигнал ошибки (t), а с выхода снимался сигнал управления u(t).
Составим блок-схему алгоритма управления рисунок 10.
По этому алгоритму составим программу коррекции, выполняемую микропроцессором, на языке Ассемблер:
CODE_SEG SEGMENT
ASUME cs: code_seg, ds: code_ceg
ORG 100 h
PP PROC
u1 db XXX
M db XXX
MET 1 IN bx; с порта
MOV ax, u1; поместить u1 в регистр общего назначения
SUBcx, bx; вычесть из cx bx, результат положить в cx
IMUL cx, M; умножить содержимое cx на M; результат полоить в cx
CMP cx, u1; сравнить содержимое cx с u1
JNE MET 1; если не равно, то перейти на MET 1
OUT cx; вывод на cx
JMP MET 1; переход на MET 1
MOV ax, 4C00h; завершение программы
INT 21 h
PP ENDP
CODE_SEG ENDS

Н ачало
ачало

u 1
1

М

u вых
вых



 (t)=u1-uвых
(t)=u1-uвых

u (t)=(t)*M
(t)=(t)*M
да
u нет


u (t)
(t)

К онец
онец
Рисунок 10. Блок-схема алгоритма управления
Исходя из двух рассчитанных методов коррекции: с помощью RC-цепочки и программы коррекции, выполняемой микропроцессором. Можно прийти к выводу, что оба метода коррекции позволяют достаточно точно скорректировать САУ. Но, исходя из того, что корректирующая RC-цепочка получилась достаточно простой в реализации, то для коррекции, данной САУ, выберем именно ее. Так как аппаратные средства коррекции обладают большим быстродействием, нежели программные.
ЗАКЛЮЧЕНИЕ
Итак, спроектированная система автоматического управления технологическим процессом электрохимических ванн является устойчивой. Все элементы рассчитанной системы относятся к неизменяемой части. Получены ЛАЧХ неизменяемой части и желаемая ЛАЧХ. Желаемая ЛАЧХ разомкнутой системы строилась, исходя из требований, предъявляемых к проектируемой системе основным показателям переходного процесса (порядок астатизма системы, допустимое время регулирования переходного процесса, требуемый запас устойчивости по фазе). По желаемой ЛАЧХ была определена передаточная функция разомкнутой системы, а по виду передаточной функции – фазовая частотная характеристика. Полученные желаемые ЛАЧХ и ФЧХ обеспечивают запас устойчивости 900, тогда как достаточным для стабильной работы системы является запас устойчивости по фазе, равный 30 400. Запас устойчивости по амплитуде также является достаточным. Для того чтобы учесть разницу между ЛАЧХ неизменяемой части и желаемой ЛАЧХ разомкнутой системы, в систему необходимо ввести корректирующее устройство в виде RC-цепочки.
СПИСОК ЛИТЕРАТУРЫ
1 Волжский автомобильный завод имени 50-летия СССР. Микропроцессорное программируемое цикловое устройство МПЦУ. Техническое описание и инструкция по эксплуатации 64.10.002.00.00.000 ТО
2 Б.Б. Некрасова. Справочное пособие по гидравлике, гидромашинам и гидроприводам. Минск: Высшая школа, 1985
3 М.З. Ганкин. Автоматизация и телемеханизация производственных процессов. Москва: Колос, 1977.
4 И.П. Копылова, Б.К. Клокова. Справочник по электрическим машинам. Москва: Энергоиздат, 1988
5 Д.Я. Понилов. Электрофизическая и электрохимическая обработка материалов. Москва: Энергоиздат, 1981
6 Т.М. Башта. Машиностроительная гидравлика. Справочное пособие. Москва: Машиностроение, 1971
7 Ю.И. Топчеев. Атлас для проектирования систем автоматического регулирования. Москва: Энергоиздат, 1988
8 В.В. Вольберг, А.Ю. Волков. Устройство и эксплуатация оборудования для металлопокрытий и металлообработке. Москва: Колос, 1982.
