2.9 Выбор нагревательного элемента

Для обогрева смесителя необходимо выбрать нагревательный элемент. Для этой цели наиболее удобно использовать нагревательные ленты ТЭН–100 А 13/3.5- Р220 УХЛ4.

Технические характеристики нагревательного элемента:

Номинальная мощность, Вт 3500.

Напряжение питания, В 220.

Постоянная времени, с 10.

Наружный диаметр оболочки, мм 13.

Развернутая длина, см 100.

Максимальный ток, А 2.

Верхний предел рабочей температуры, ⁰С 500.

Расчёт передаточной функции нагревательного элемента.

Передаточная функция нагревательного элемента имеет вид:

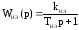, (35)

где 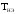– постоянная времени прибора;

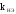– коэффициент передачи:

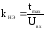, (36)

где t_max – верхний предел рабочей температуры;

U_вх – входное напряжение:

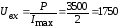В, (37)

.

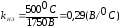Тогда передаточная функция нагревательного элемента будет иметь вид:

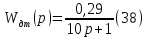
3. РАСЧЕТ УСТОЙЧИВРСТИ СИСТЕМЫ

3.1 Устойчивость системы

Структурная схема системы автоматического управления приготовления асфальтового покрытия имеет вид, показанный на рисунке 3.

W7

W4

W5

W6

W1

W2

W3

W8

W9

Рисунок 3 – Структурная схема замкнутой системы автоматического управления приготовления асфальтового покрытия.

Передаточные функции блоков имеют вид:

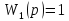
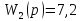
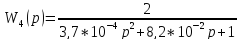
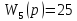
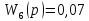
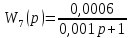
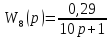
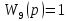
Рассчитаем передаточную функцию замкнутой системы.

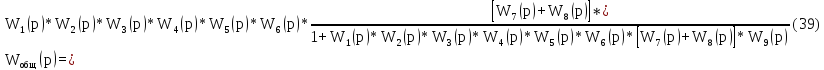
Используя программу Mathсad, подставив значения функций, получим

выражение общей передаточной функции замкнутой системы автоматического управления:

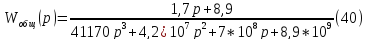
Оценим устойчивость системы. Оценку устойчивости проведем по критерию устойчивости Гурвица.

Обозначим:

а₀=41170; а₁=4,2*10⁷; а₂=7*10⁸; а₃=8,9*10⁹.

Необходимое условие устойчивости выполнено - все коэффициенты характеристического уравнения положительные.

Составим определители Гурвица:

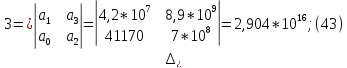
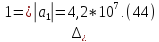
Так как все определители Гурвица положительные, то выполняется и достаточное условие устойчивости системы. Таким образом, система устойчива.

3.2 Прямые оценки качества системы

Чтобы определить показатели качества, строится график переходного процесса, используя программу Mathсad.

Для этого находится обратное преобразование Лапласа от передаточной функции замкнутой системы.

(45)

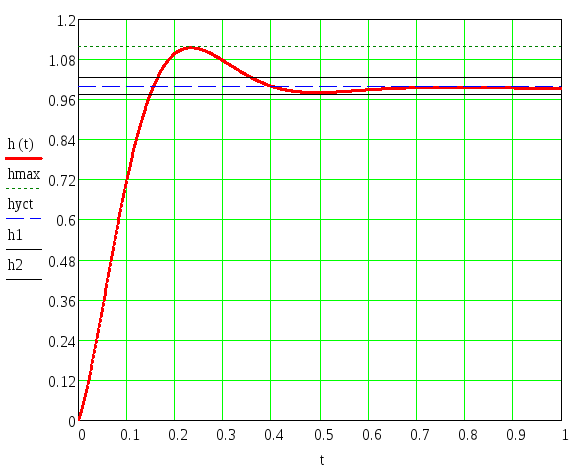
Рисунок 3- Переходный процесс системы.

По графику переходного процесса определим прямые оценки качества системы:

1) Максимальное значение переходного процесса:

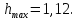
2) Установившееся значение переходного процесса:

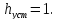
3) Время переходного процесса, ограниченное пятипроцентной трубкой, которая определяется интервалом регулируемой величины:

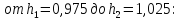
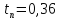c

4) Перерегулирование:

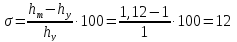
5) Колебательность: n=2.

6) Время нарастания регулируемой величины:

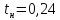c

7) Время первого согласования:

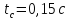
Можно сделать вывод: по переходному процессу видно из рисунока 3, что система является устойчивой, были определены прямые оценки качества системы, такие как перерегулирование и время регулирования, которые удовлетворяют заданным в техническом задании параметрам системы.

3.3 Косвенные оценки качества системы

Определим амплитудно-частотную функцию замкнутой системы:

Передаточная функция для замкнутой системы:

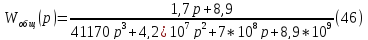
Для того, чтобы определить амплитудно-частотную характеристику системы, необходимо в передаточной функции заменить p на jω, знаменатель уравнения помножить на сопряженное выражение, выделить мнимую и вещественную части, и по следующей формуле строится амплитудно-частотная характеристика системы:

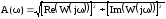. (47)

Построим график АЧХ замкнутой системы, используя программу Mathсad.

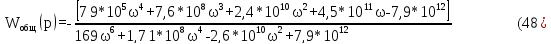
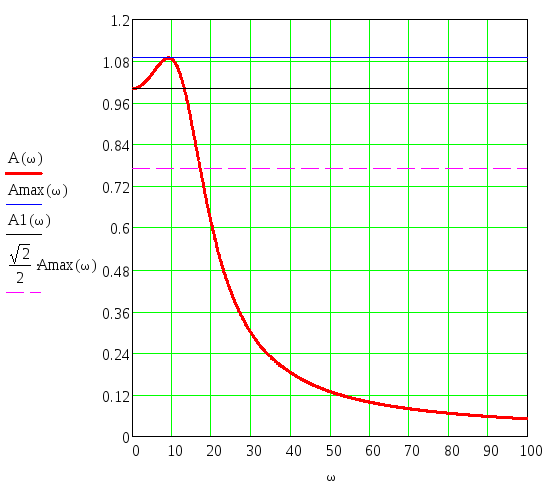
Рисунок 4- Амплитудно-частотная характеристика системы.

Определим косвенные оценки качества по полученным зависимостям:

1) Максимальное значение АЧХ:

2) Показатель колебательности:

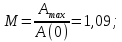
А(0)=1.

3) Резонансная частота:

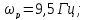
4) Частота среза:

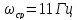
5. Полоса пропускания:

Далее проведём перпендикуляр на ось абсцисс и получим граничные частоты:

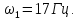
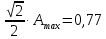
3.4 Проверка дискретной системы на устойчивость с помощью критерия Шур-Кона

Проверка устойчивости системы автоматического регулирования с учетом микропроцессора выполняется на основании критерия устойчивости Шур-Кона, который позволяет анализировать устойчивость дискретных и дискретно-непрерывных систем по характеристическому уравнению замкнутой системы, записанному в форме z-преобразования.

Найдем дискретную передаточную функцию замкнутой системы. Для этого необходимо провести z – преобразований.

, (49)

В курсовом проекте примем отношение 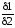= 1

Период дискретизации T = 0,01 с.

Воспользовавшись программным продуктом MathLab можно получить передаточную функцию

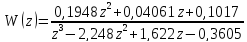(50)

Листинг программы:

>> A=tf([190000000 8900000000],[41170 4200000 70000000 890000000])

Transfer function:

1.9e008 s + 8.9e009

-------------------------------------------

41170 s^3 + 4.2e006 s^2 + 7e007 s + 8.9e008

>> Ad = c2d(A, 0.01)

Transfer function:

0.1948 z^2 + 0.04061 z - 0.1017

----------------------------------

z^3 - 2.248 z^2 + 1.622 z - 0.3605

Sampling time: 0.01

>> step(Ad)

Рисунок 5- График переходного процесса после z-преобразования

По виду переходного процесса видно, что система является устойчивой. Можно сделать вывод, что при введении в систему микропроцессора, качество системы не ухудшается, а значит, дискретная часть системы также является устойчивой.

Алгебраический критерий Шур-Кона позволяет анализировать устойчивость импульсных систем регулирования по характеристическому уравнению замкнутой системы, записанной в форме z-преобразования.

Характеристическое уравнение – знаменатель (50) – в данном случае имеет вид:

D(z)=z³-2,248z²+1,622z-0,3605 (51)

Коэффициенты характеристического уравнения:

а₀=1; а₁=-2,248; а₂=1,622; а₃=-0,3605.

Рассчитаем диагональные миноры:

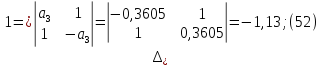
(53)

(54)

Как видно из расчета четные миноры больше нуля, нечетные – меньше нуля.

Следствием этого является устойчивость дискретной системы.