
- •Задания для самостоятельной работы
- •По дисциплине
- •«Математические методы теоретической физики»
- •Симферополь 2008
- •1.Распределение учебного времени, отводимого на дисциплину
- •Содержание тем самостоятельной работы для курса "Математические методы теоретической физики"
- •Занятие № 2
- •Занятие № 3
- •Занятие № 4
- •Занятие № 5
- •Занятие № 6
- •Занятие№ 7
- •Занятие № 8
- •Занятие № 9
- •Занятие № 10
- •Занятие № 11
- •Занятие № 12
- •Занятие № 13
- •Занятие № 14
- •Занятие № 15
- •Занятие№ 16
- •Занятие № 17
- •Занятие № 18
- •Занятие № 19
- •Занятие № 20
- •Занятие № 21
- •Занятие № 23
- •Занятие № 24
- •Задание № 25
- •Литература:
Занятие № 11
1. Вычислить
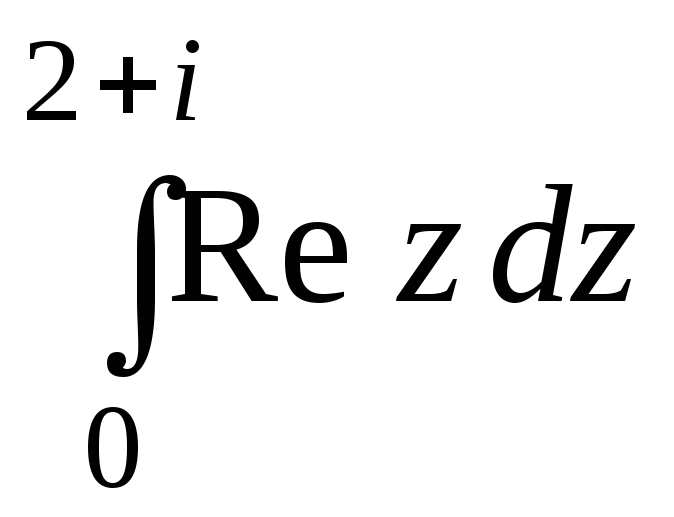 .
.
Если
путем интегрирования служит прямоугольный
отрезок z
= (2+i)t,
(![]() );
вычислить этот же интеграл, приняв за
путь интегрирования ломаную, первое
звено которой есть прямолинейный отрезок
[0, 2], а второе – отрезок [2,2+i].
);
вычислить этот же интеграл, приняв за
путь интегрирования ломаную, первое
звено которой есть прямолинейный отрезок
[0, 2], а второе – отрезок [2,2+i].
2. Вычислить
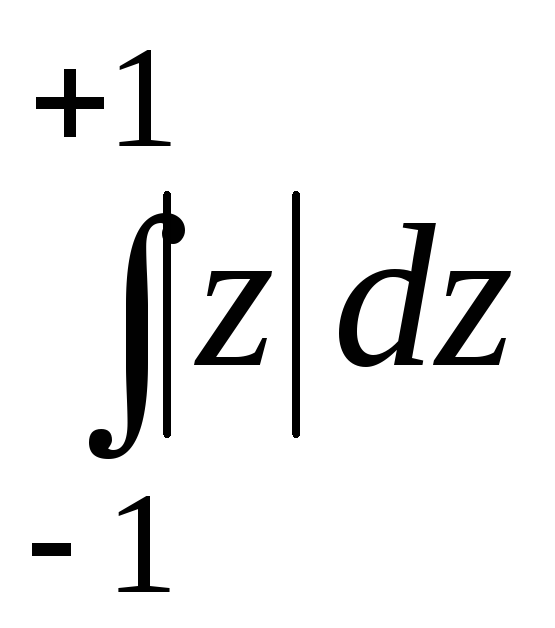 ;
;
когда путями интегрирования служат:
а) прямолинейный отрезок;
б) верхняя половина окружности радиуса единица;
в) нижняя половина этой окружности.
3. Вычислить
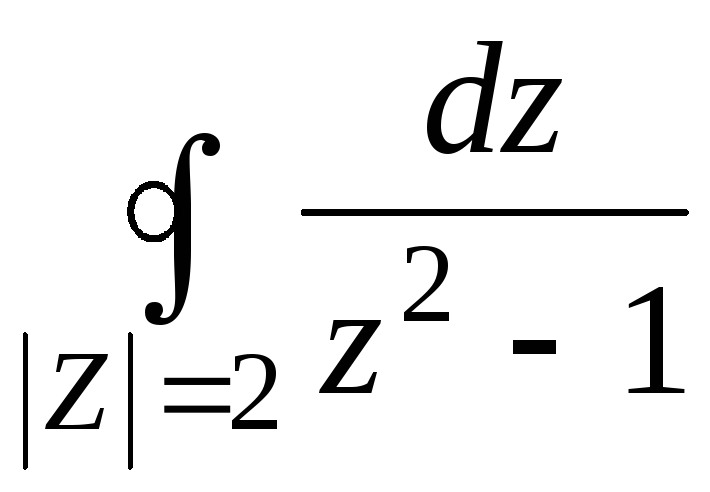 ,
,
![]()
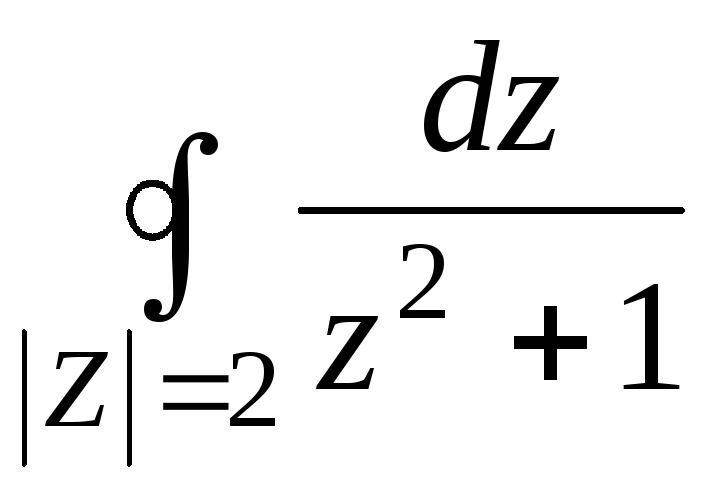 ,
,
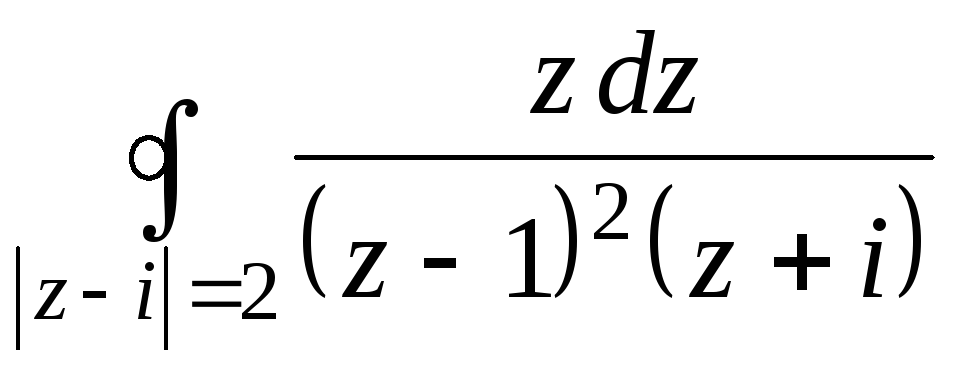 .
.
-
Занятие № 12
-
Разложить главное значение функций в степенной ряд в окрестности
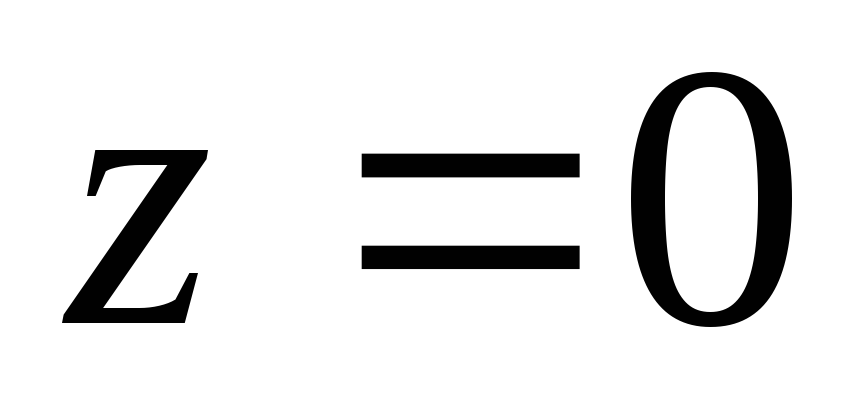
![]()
-
Вычислить первые четыре коэффициента степенного ряда для функций:
а)
![]() ,
б)
,
б)
![]() ,
в)
,
в)
![]()
-
Разложить в ряд Лорана функцию
 при
при
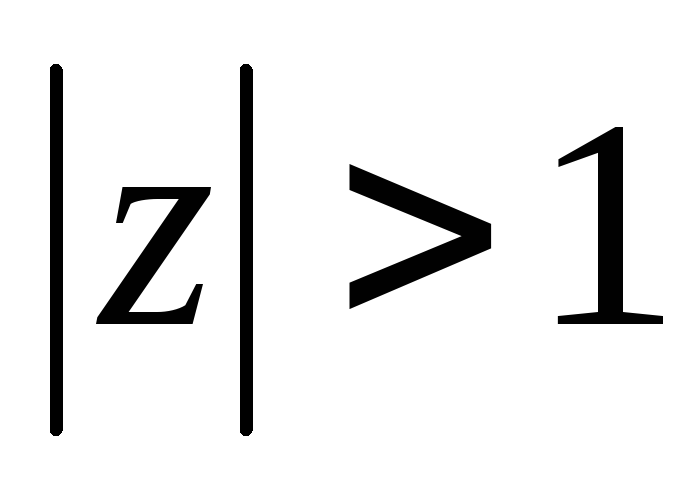 .
.
-
Разложить в ряд Лорана функцию
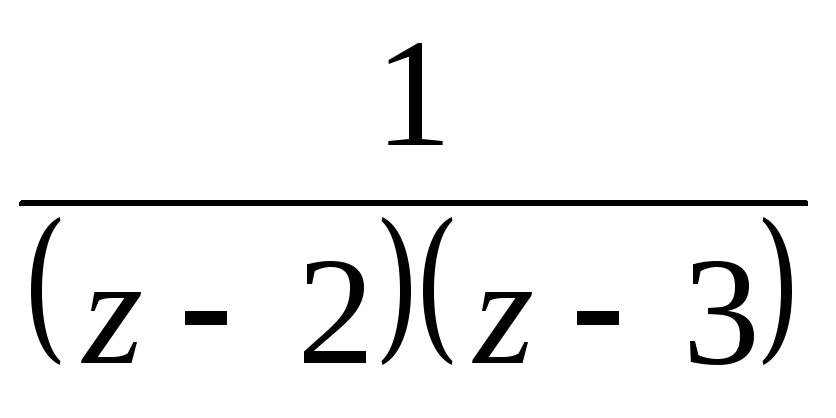 при
при
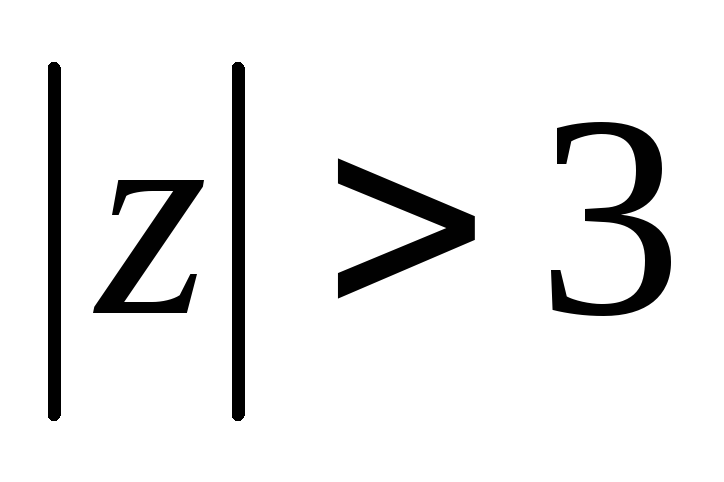 .
.
-
Какие особенности имеют функции:
а)
![]() при
при
![]() ,
б)
,
б)
![]() при
при
![]() ,
в)
,
в)
![]() при
при
![]() ,
,
г)
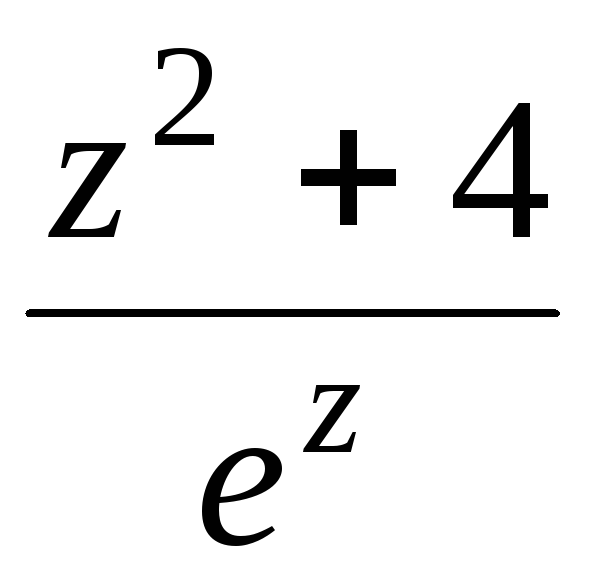 при
при
![]() ,
д)
,
д)
![]() при
при
![]() ,
е)
,
е)
![]() при
при
![]() .
.
-
Занятие № 13
1. Найти вычеты функций
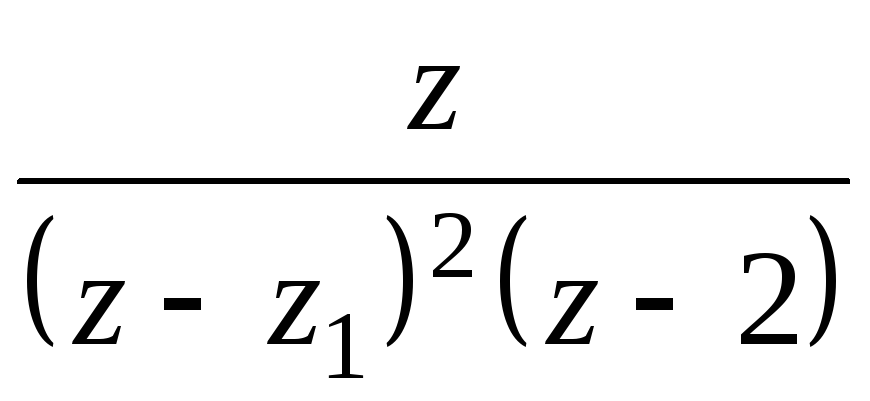 ,
,
![]()
2.Вычислить интегралы
а)
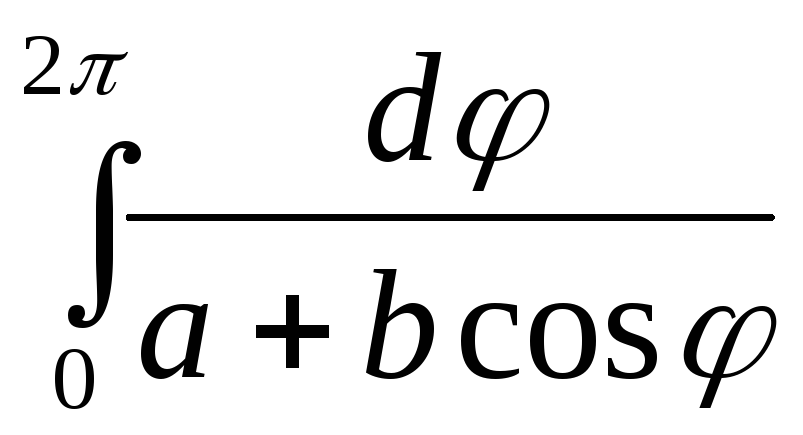 ,
б)
,
б)
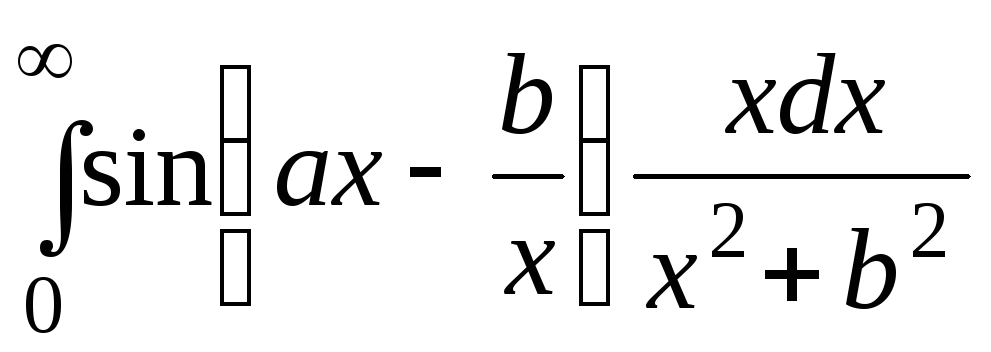 , в)
, в)
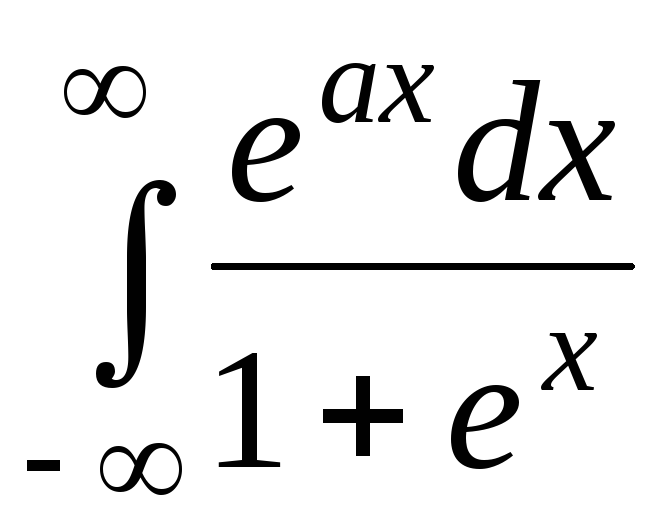 ,
,
г)
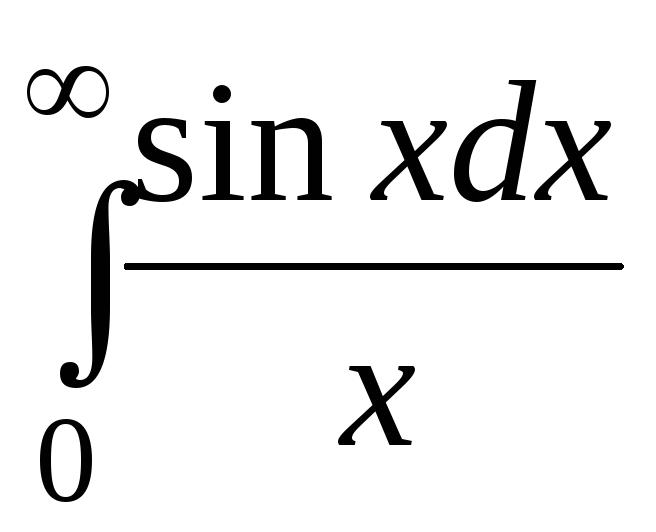 , д)
, д)
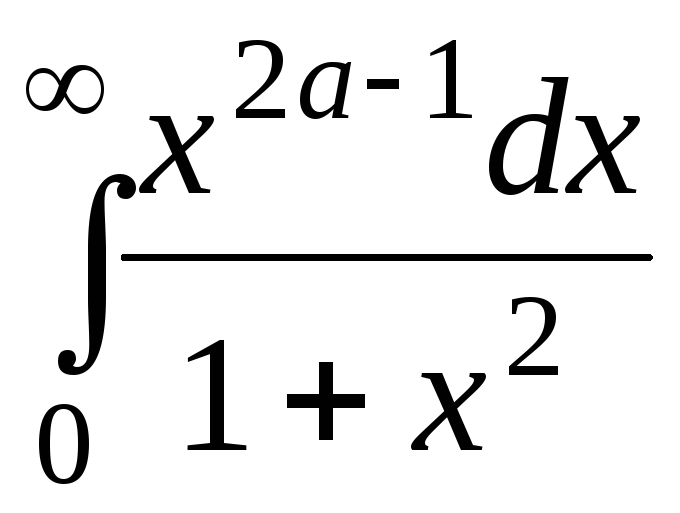 , е)
, е)
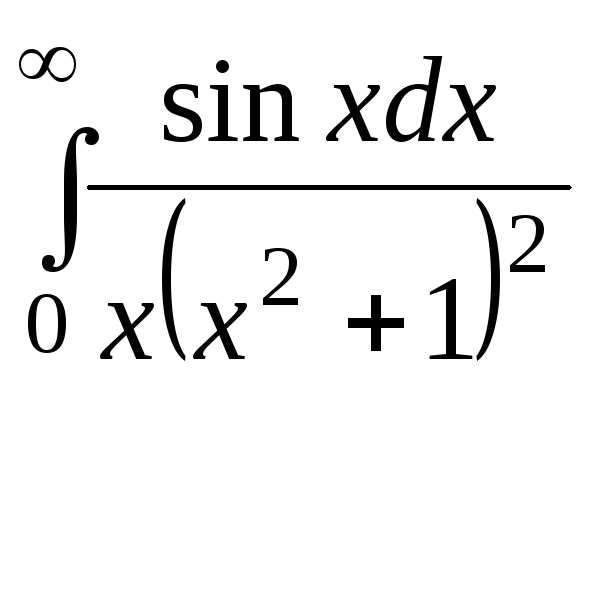 , ж)
, ж)
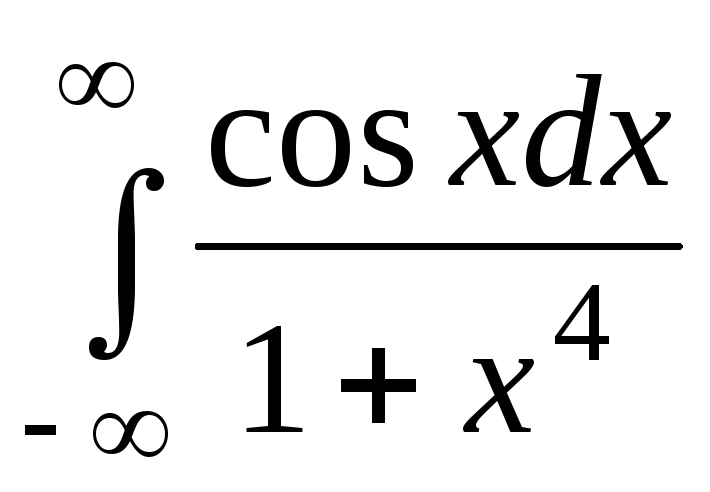
з)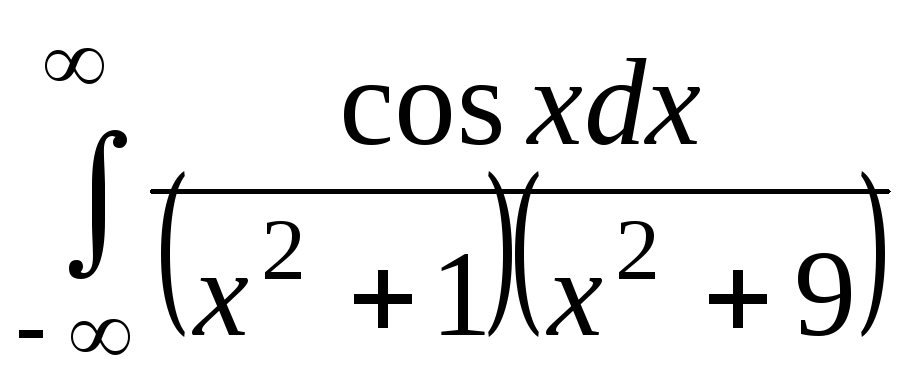
Занятие № 14
-
Доказать, что
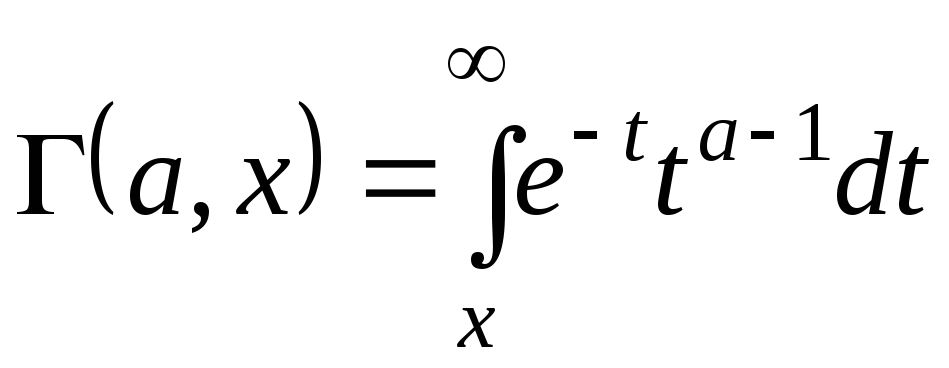
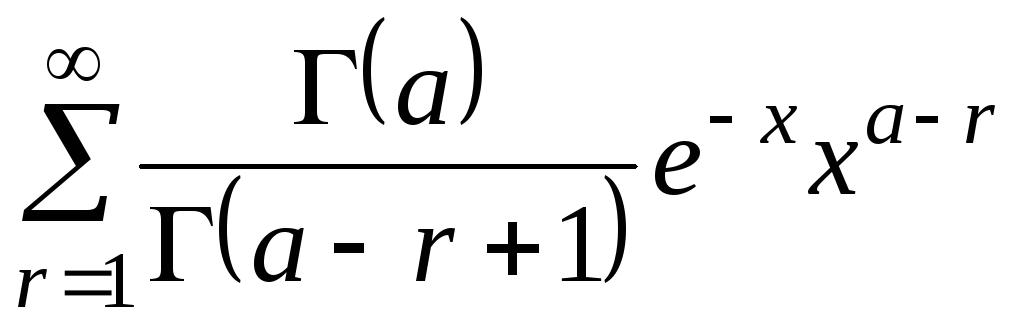 ,
при
,
при
![]() x
x![]()
2. Доказать, что
Erfc
T=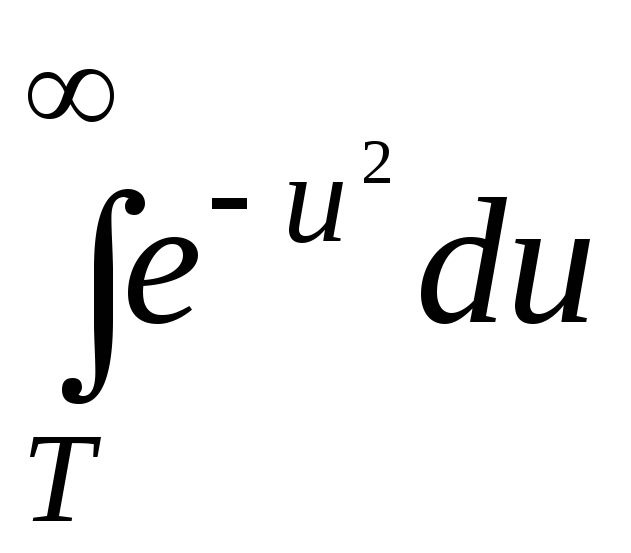
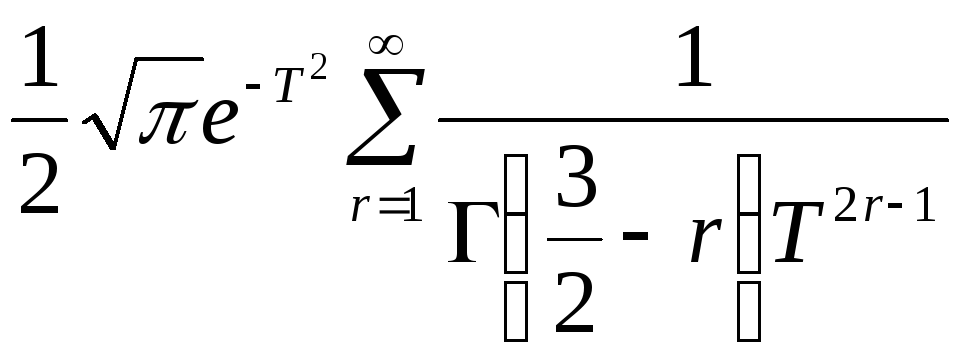 ;
;
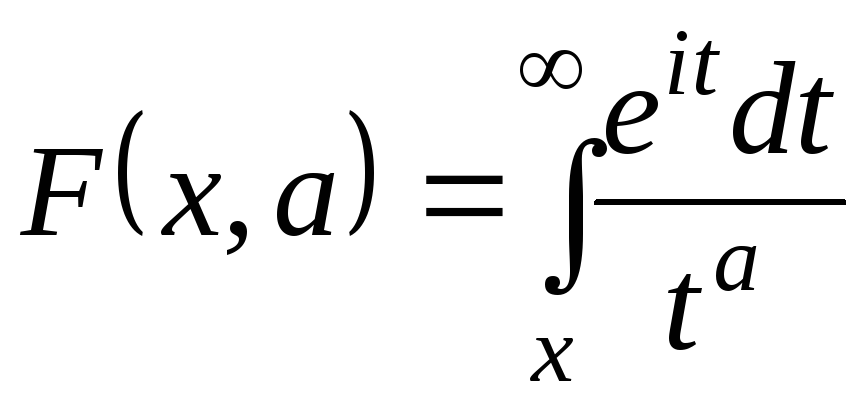
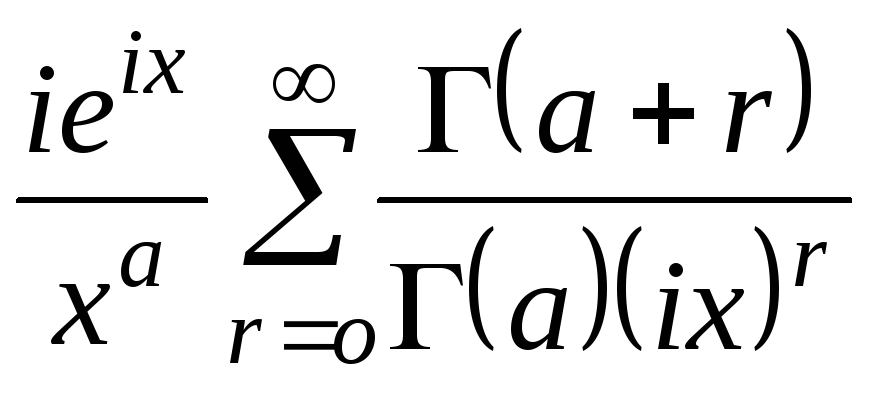 ;
;
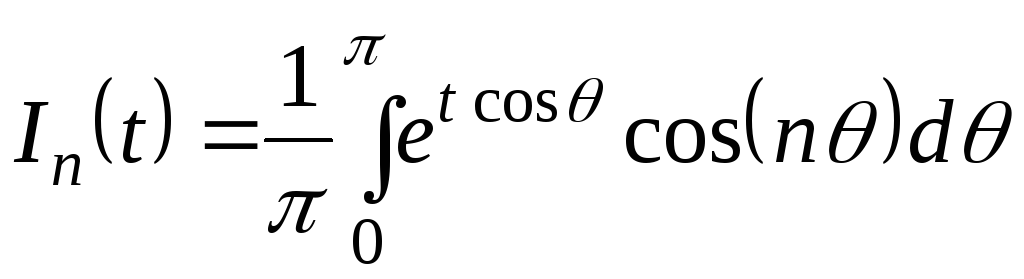
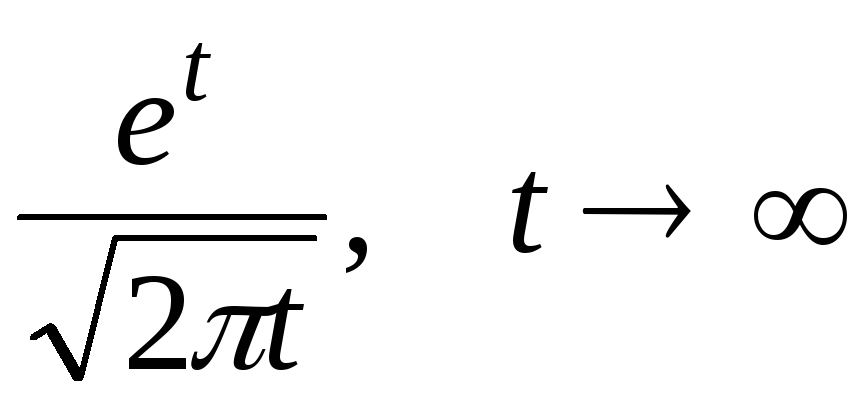 ;
;
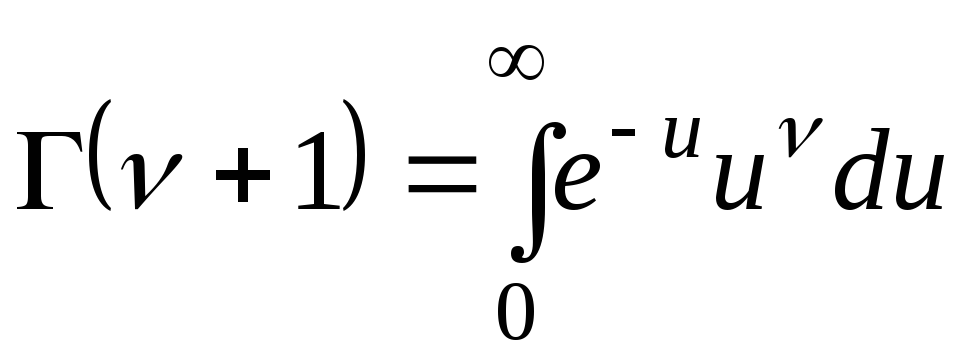
![]()
-
Занятие № 15
-
Показать, что при
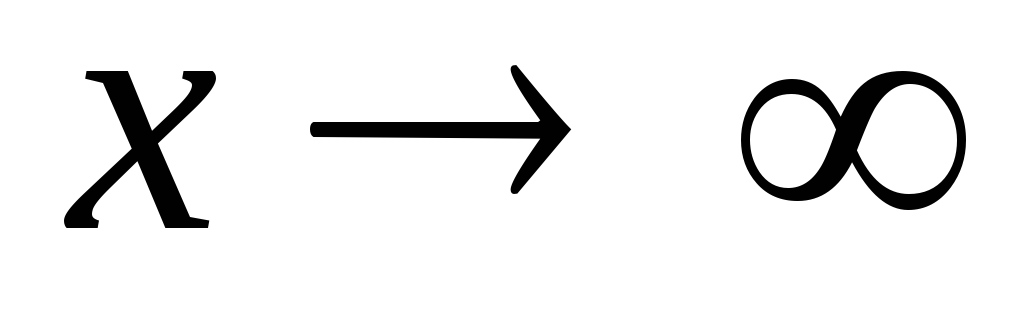
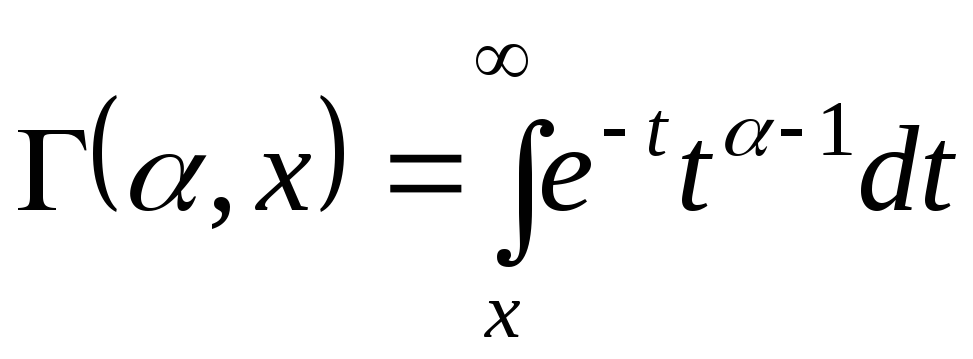
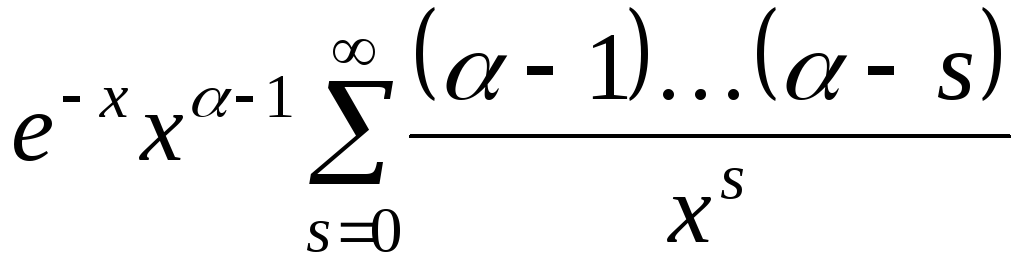
-
Доказать, что
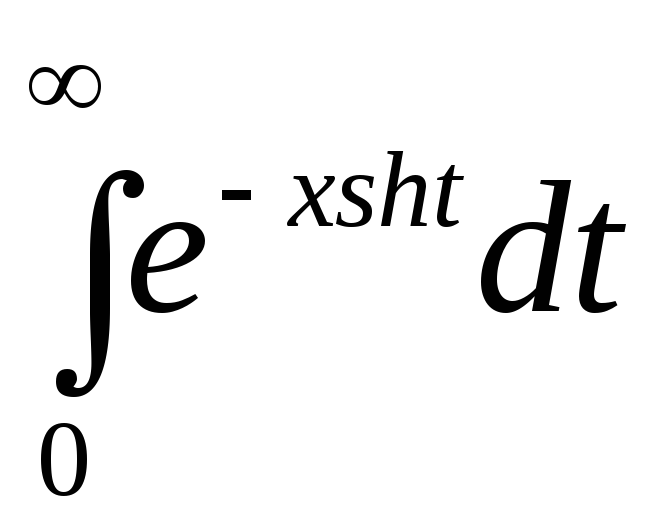 ~
~
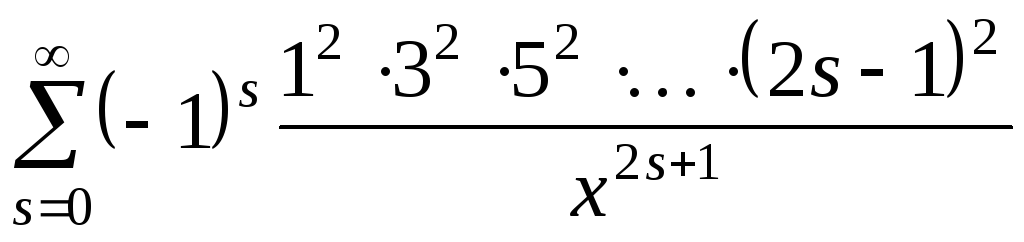 ,
,
![]()
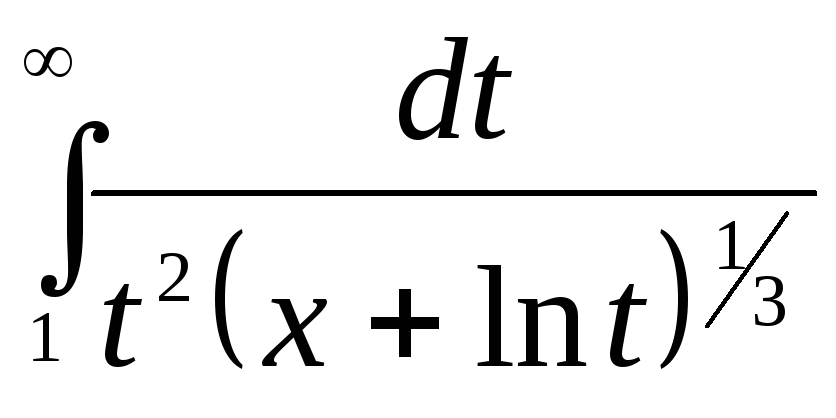 ~
~
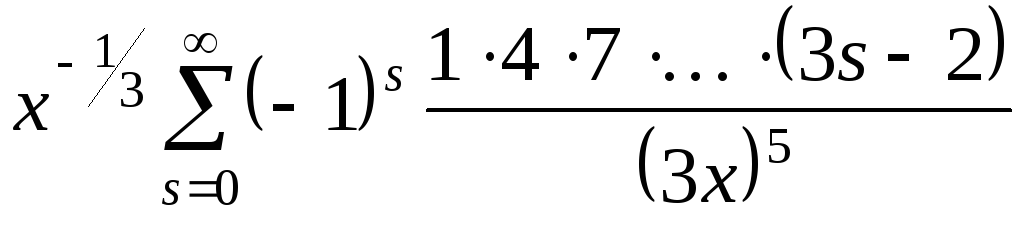 ,
,
![]()
-
Показать, что
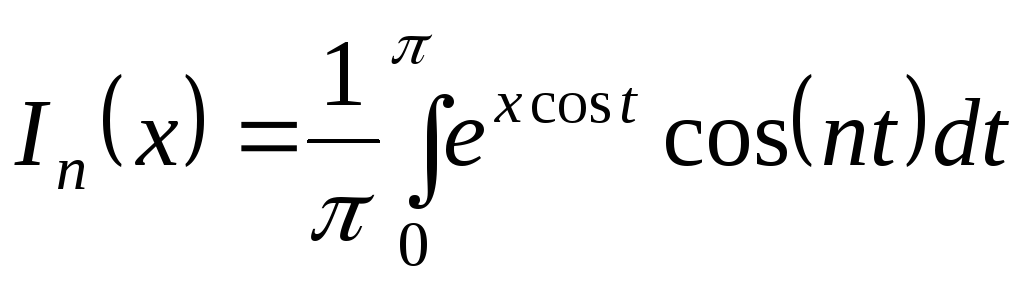 ~
~
![]() ,
,
![]()
-
Показать, что
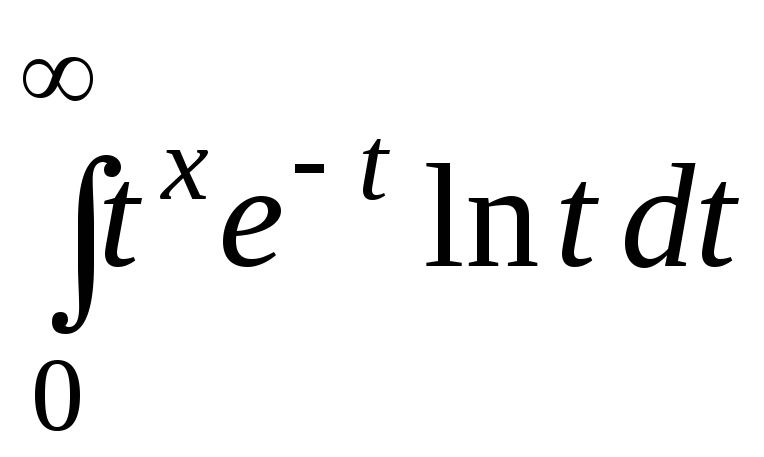 ~
~
![]() ,
,
![]()
-
Занятие№ 16
1. Зная центр α и радиус r окружности, определить положение
центра и величину радиуса окружности, являющейся инверсией
данной, принимая полюс в начале координат и радиус инверсии
равен R.
2.
Написать линейное преобразование
единичного круга самого в себя, зная
двойные точки
![]() , 2 и точку
, 2 и точку
![]() , переходящую в
, переходящую в
бесконечность.
3. Написать линейное преобразование единичного круга самого в себя,
зная двойные точки i , -i и точку 2i , переходящую в
бесконечность.
4. Написать линейное преобразование единичного круга самого в себя,
зная его двойную точку 1 и точку 1+ i , переходящую в
бесконечность.
Занятие № 17
-
Составить линейное преобразование верхней полуплоскости на единичный круг, переводящее точки действительной оси –1, 0, +1 в точки +1, i, -1 окружности.
-
Показать, что при конформном отображении z = x + iy =
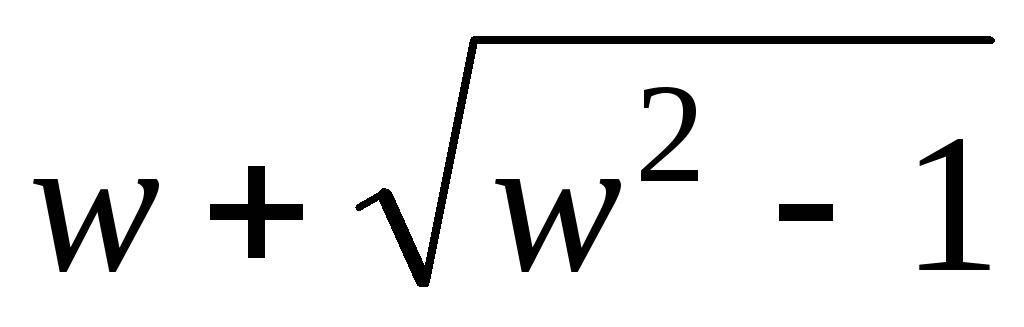 (
(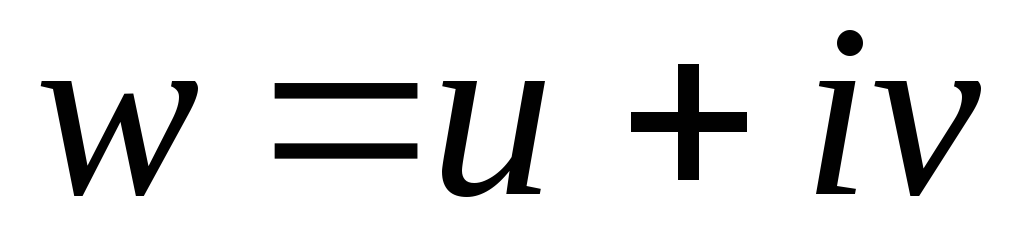 )
действительная ось плоскости
)
действительная ось плоскости
 переходит в участок
переходит в участок
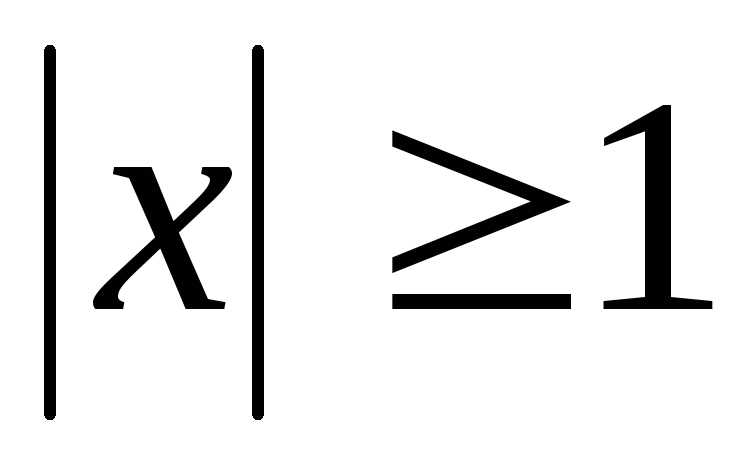 действительной оси плоскости z
и в единичную
окружность z
=
действительной оси плоскости z
и в единичную
окружность z
=
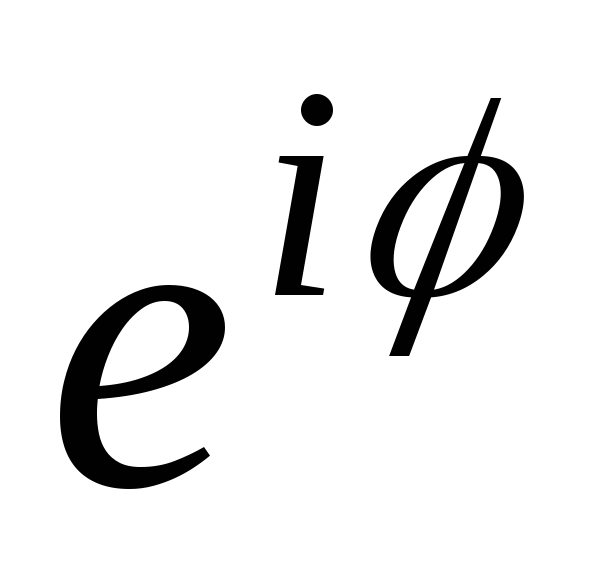 .
.
Занятие № 18
-
Проверить, что последовательности
а)
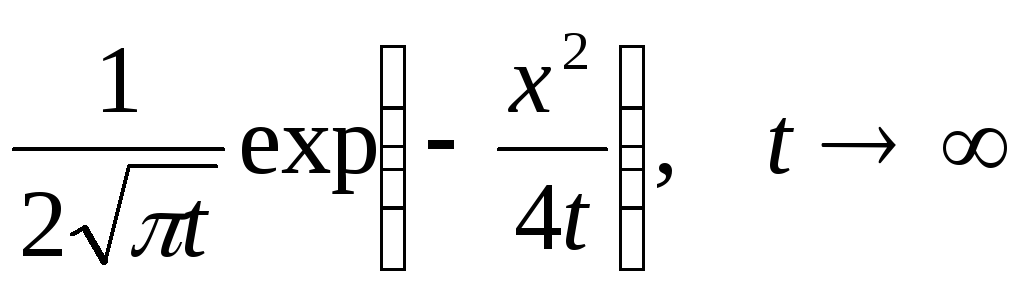
б)
![]()
в)
![]()
г)
![]()
есть δ-функциональные.
-
Доказать, что
а)
![]()
б)
![]() ,
где
,
где
![]() -
целая часть числа.
-
целая часть числа.
-
Доказать, что
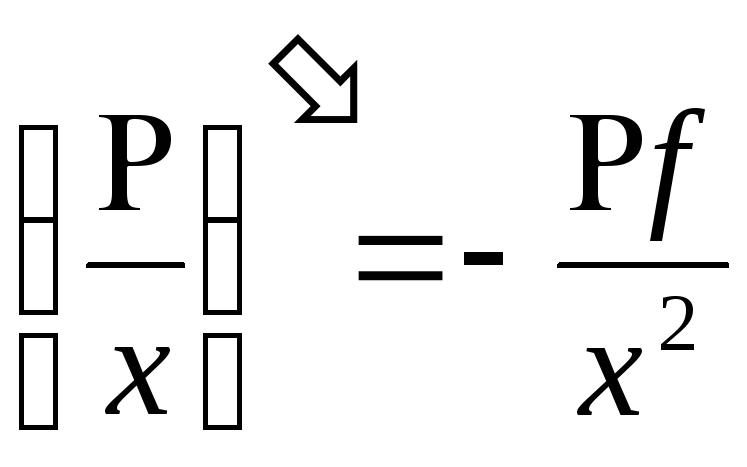
-
Доказать, что
а)
![]()
б)
![]()
в)

-
-
Занятие № 19
-
Доказать
![]() ;
;
-
Доказать
![]()
-
Доказать
a)
![]()
b)
![]()
c)
![]() .
.
-
Доказать, что
![]()
