3. Частотные критерии устойчивости многоконтурных сар по Михайлову-Найквисту

Для анализа устойчивости многоконтурных систем воспользуемся логарифмическими частотными характеристиками.

Многоконтурная САР с замкнутой главной обратной связью будет устойчива, когда во всех входящих в нее передаточных функциях, имею­щих m полюсов в правой полуплоскости, при Lm > О обеспечивается раз­ность между числом подъемов и спусков пересечений прямых с = -180°, -540°, -900° ... всеми фазовыми частотными характеристиками, получае­мыми путем последовательного замыкания каждого из контуров обратны­ми связями, равнымиm/2.

4. Выделение областей устойчивых и неустойчивых состояний с по­мощью d-разбиения

Применение метода D-разбиения позволяет исследовать устойчи­вость замкнутой системы с помощью характеристического уравнения на плоскости, выделяя один или два параметра. В качестве таких параметров могут быть приняты передаточные коэффициенты или постоянные времени передаточных функций

Рассмотрим (67)

Из выражения (67) найдем: (68)

Положим, что w – комплексное число, и отобразим мнимую ось плоскости корней на плоскостьw. Тогда при из уравнения (67) получим:

(69)

или .

Изменяя значения w от до, построим в плоскостиw (или и, v) кривую, отображающую мнимую ось jw плоскости S на плос­кость w(jw). Получаемая в результате этого кривая является кривой D-разбиения. Такая кривая всегда симметрична относительно действитель­ной оси; поэтому можно строить лишь участок, соответствующий измене­нию чистоты от 0 до , а затем дополнить его зеркальным отображением кривой D-разбиения относительно действительной оси. В результате по­лучим несколько областей. Однако судить о том, в какой из областей все корни характеристического уравнения имеют отрицательные дей­ствительные части, не представляется возможным. Для этого необходимо пользоваться правилом штриховки кривых D-разбиения, Сформулируем это правило применительно к D-разбиению плоскости относительно одно­го параметра или , в следующем виде.

При перемещении вдоль кривой D-разбиения от частоты доее следует штриховать слева, как показано на рисунке 2. Та­ким образом, на плоскости получим несколько зон, отделенных одна от другой кривойD-разбиения.

Рассмотрим рисунок 2, а, где показаны три области 1-3. Будем счи­тать, что в зоне 1 каждой точке плоскости соответствует комплексное чис­ло к корней с отрицательной действительной частью. Если при переходе из зоны 1 в зону 2 происходит пересечение кривой D-разбиения с не заштри­хованной стороны на заштрихованную, то в зоне 2 число корней с отрица­тельной действительной частью увеличивается на единицу и отметка точки к становится равной к+ 1. При переходе кривой D-разбиения из зо­ны 1 с заштрихованной стороны на не заштрихованную (зона 3) число корней с отрицательной частью уменьшается на единицу, и отметка точки будет равна к—1.

Интерес представляет исследование только действительных значе­ний параметра w. Поэтому, построив кривые D-разбиения, находят такой отрезок действительной оси на плоскости w(jw), который принадлежит об­ласти устойчивости. Равенство числа отрицательных корней степени ха­рактеристического уравнения позволяет выделить зону, где точки плоско­сти с наибольшим числом соответствуют области устойчивости системы. Числовые значения на действительной оси в этой области определяют принятые параметры или .

Из рисунка 2, а можно установить, что в зоне 2 имеется самая большая отметка точки к + 1, и если она равна п, то в зоне 2 обе­спечивается устойчивость. Числовые значения по оси абсцисс для рас­сматриваемого параметра в области 2 гарантируют устойчивость работы системы. На рисунке 2, б изображена кривая D-разбиения с пятью зонами I-V. В зонах // и V обеспечивается условие к+1=п и система устойчива. Кривая D-разбиения (рисунок 2, в) выделяет две зоны. В зоне // будет точ­ка с отметкой к +1=п. Она соответствует устойчивости системы. В за­ключение воспользуемся кривыми D-разбиения, приведенными на рисунке 2, г. При этом видно, что наибольшая отметка числа к в зоне /; при к =п зона / является областью устойчивости.

Для удобства вычислений можно брать w = 0 и находить корни ос­тавшегося уравнения. При их числе, равном с отрицательными действительными частями, имеемk=, а область устойчивости системы будет иметь отметку с точкой(где=1,2,3,…), равной порядку характеристического уравненияn. Воспользуемся данным положением. Допустим, что кривая D – разбиения, изображенная на рисунке 2, в, построена по характеристическому уравнению вида:

(70)

где постоянные коэффициенты.

Это нетрудно показать, если уравнение (70) можно переписать в виде

(71)

Пусть s=w; тогда выражение (71) будет иметь вид

(72)

Задаваясь в уравнении (72) различными значениями w, построим на рисунке 2, в, кривую D – разбиение.

Теперь положим ; тогда из уравнения (72) получим

(73)

откуда

Из уравнения (73) определим .

Итак, устанавливаем, что один корень имеет нулевое значение, а в трех остальных действительные части отрицательны, т.е. . Так как в зоне 2k+1=i+, то при i=1 найдем k+1=4, так как порядок уравнения (73) четвертый. Следовательно, зон 2 соответствует устойчивой системе. При этом ее параметр изменяется в диапазоне действительных чисел, выделенных на рисунке 2, в, жирной стрелкой.

Перейдем теперь к рассмотрению САР, в которых можно выделить два параметра и. Если эти параметры входят в характеристическое уравнение (70) линейно, то его можно переписать в виде:

(75)

При из уравнения (75) получим

(76)

Для построения кривой D – разбиения необходимо определить ипри различных значенияхw, решая совместно уравнения: .

В результате из выражений (75) и (76) найдем два уравнения, в которых можно выделить и, т.е.

(77)

Пользуясь соотношениями и изменяя w отдополучим в системе координаткривыеD – разбиения.

Сформулируем правило штриховки кривой D-разбиения, постро­енной относительно двух параметров.

При перемещении вдоль кривой D – разбиения от частоты до ее следует штриховать слева кривой в тех точках, для которыхи справа при. Отметим, что при изменении со криваяD-разбиения пробегает дважды от w=0 до w=+и доw=, и ее следует вы­делять двойными штрихами.

На рисунке 3, а изображены две различные кривые D-разбиения, которые обозначены цифрами 1 и 2. Из рисунка 3,а видно, что если переход через кривую 2 от точки к происходит с не за­штрихованной стороны на заштрихованную, то число корней с отрица­тельной действительной частью увеличивается на два и отметка точки к становится к + 2.

Рис. 2. Кривые D – разбиения по одному параметру на пл. w для определения областей устойчивых и неустойчивых состояний систем: а, в, г – с тремя областями; б – с пятью областями.

При переходе кривой 1 из зоны с заштрихованной сторо­ны на не заштрихованную число корней с отрицательной действительной частью уменьшается на два и точка отмечается как к— 2.

При движении по кривой D-разбиения в плоскости двух параметров знак может изменяться только в бесконечности или при частотахw, ко­торым соответствуют особые прямые. В результате этого направление штриховки кривой Д-разбиения меняется только в тех точках, где кривая пересекается с особыми.

Рассмотрим особую прямую при w=0 (рисунок 3, б); тогда вблизи этой точки прямую штрихуют одинарной штриховкой, совпадающей с двойной штриховкой кривой D-разбиения. Особую прямую при w= штрихуют таким же образом, как и при w=0 (рисунок 3, в). Кроме особых прямых w=0 и w=, существуют особые прямые, соответствующие тем значениямw=при которых одновременно удовлетворяются условияТакую особую прямую вблизи точкиw=и штрихуют двой­ной штриховкой, совпадающей с двойной штриховкой кривойD-разбиения (рисунок 3, г). На рисунке 3, а— г приведена разметка точек при пересечении кривых D-разбиения.

Сравнение различных методов анализа устойчивости САР рассмотрим на примере.

Пример. Допустим, что САР дизеля можно представить с помощью передаточной функции:

где аимогут принимать различные значения в диапазоне.

При принятых числовых значениях параметров составим характеристическое уравнение: , т.е.

(78)

Уравнение (78) при изапишем в общем виде:

(79)

Рис. 3. Кривые fl-разбиения по двум параметрам и на пл. w для оп­ределения областей устойчивых и неустойчивых состояний: а - иллюстрирующие правило штриховки кривых; б - при наличии особой прямой, проходящей через точку w= 0; в - при наличии особой прямой, проходящей через точку w=;г— при наличии особой прямой, проходящей через точку w= где .

Введем в уравнение (79) новую переменную тогда получим:

(80)

или (81)

Здесь

Перепишем уравнение (81) в виде следующей системы уравнений:

(82)

Зададимся квадратичной формой: и будем искать функцию Ляпунова в форме:

удовлетворяющей, с учетом системы уравнений (82), соотношению

Соответствующая система для определения коэффициентов имеет вид:

(83)

где

Определитель системы уравнений будет

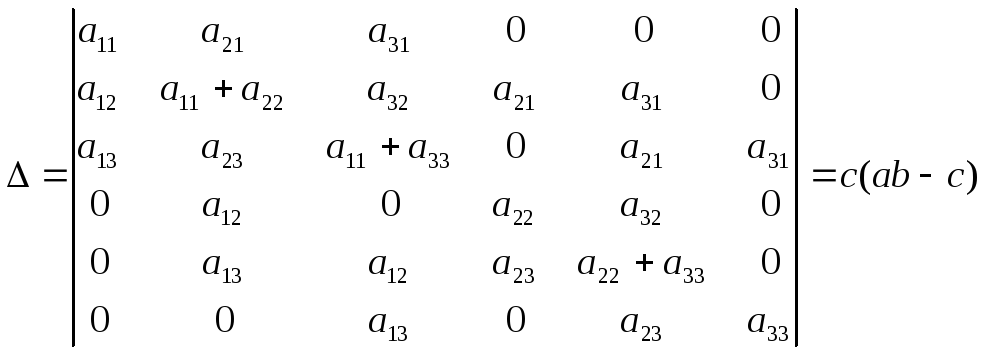(84)

Запишем функцию Ляпунова тогда. Пустьт.е. всепри всехза исключениемиИмея это в виду, запишем функцию Ляпунова как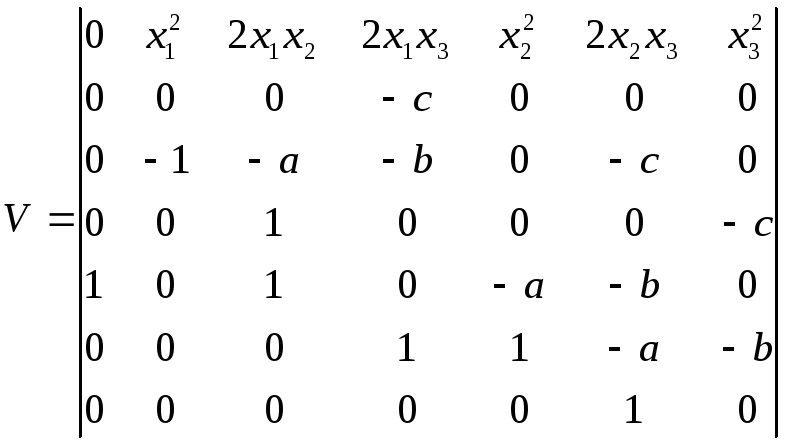

откуда (85)

или

и .

Условиями положительной определенности функции V по критерию Сильвестра являются которые одновременно характеризуют отрицательную определенностьW. Так как ато неравенства можно переписать в видеили

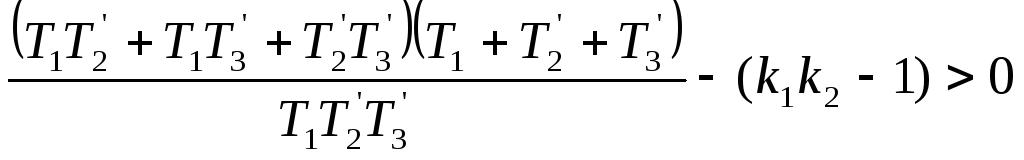(86)

Рис. 4. Сравнение областей устойчивых и неустойчивых состоя­ний по параметрам и полученных на основе различных методов.

Подставив в неравенство (86) числовые значения, найдем уравнения Границы областей устойчивых и неустойчивых состояний: .

По формуле (87) определим числовые значения, характеризующие границы устойчивости по Ляпунову при различных и

	0,05	0,1	0,2	0,3	0,45	1,0	2,0	3,0	5,0	10
	8,98	7,0	6,1	5,9	5,82	6,1	7,0	7,9	9,9	15

По этим числовым данным строим границу областей устойчивости (кривая 1, рисунок 4). Для определения минимального значения вос­пользуемся соотношением

(88)

откуда T_{l mi} = 0,450 с.

Кривая 1 имеет две асимптоты, определяемые уравнениями =0 — ось ординат и k=4,9383 + 0,98777Т-наклонная асимптота (прямая 2). Асимптоты показаны штриховыми линиями. Область устойчивости системы выделена на рисунок 4 штриховкой.

Воспользуемся для построения границ областей устойчивости крите­рием Льенара - Шипара. Если характеристическое уравнение имеет 3-й порядок, то условия устойчивости Льенара — Шипара будут

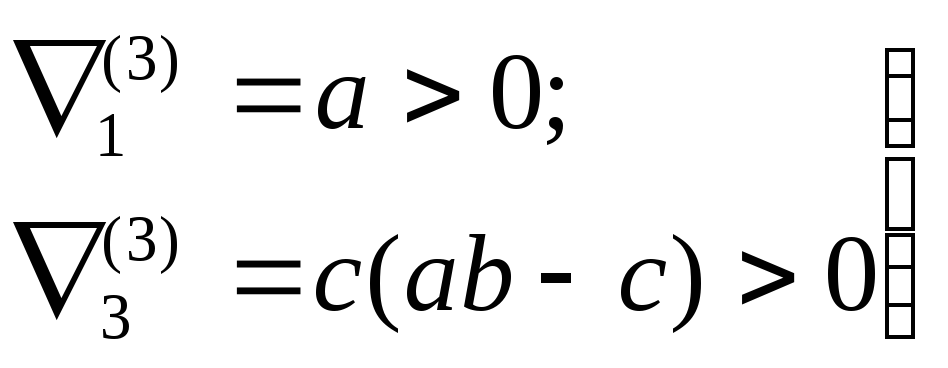(89)

Из неравенств (89) видно, что последние аналогичны условиям ус­тойчивости по первому методу Ляпунова. Поэтому, пользуясь этим крите­рием, получим полное совпадение с кривой 1, которая ранее была построена на рисунке 4.

Исследуя устойчивость системы с помощью построения частотных характеристик, найдем

(90)

Задаваясь значениями и построим семейства логарифмических амплитудных и фазовых частотных характеристик. Они показаны на рисун­ке 5,а при с,k =7,04; на рисунке 5,6 при T= 0,3 с, k = 5,9; на рисун­ке 5, в при Т=1 с, = 6,13 и на рисунке 5, г приT= 3 с, k = 7,97. Из рисунка 5,а—г видно, что системы в замкнутом состоянии при этих параметрах на­ходятся на грани устойчивости, так как их запасы устойчивости по фазе УФ = 0°. По числовым значениям и строим на рисунке 4 кривую 1, кото­рая совпадает с ранее полученной. Следовательно, частотный графоанали­тический метод анализа устойчивости также позволяет выделять области ус­тойчивых и неустойчивых состояний замкнутой системы. Данный метод ре­комендуется использовать при относительно высоких порядках передаточ­ных функций разомкнутых систем.

В заключение рассмотрим возможности метода D-разбиения при ис­следовании устойчивости систем. Для этого воспользуемся следующей формой представления дифференциального уравнения:

(91)

где

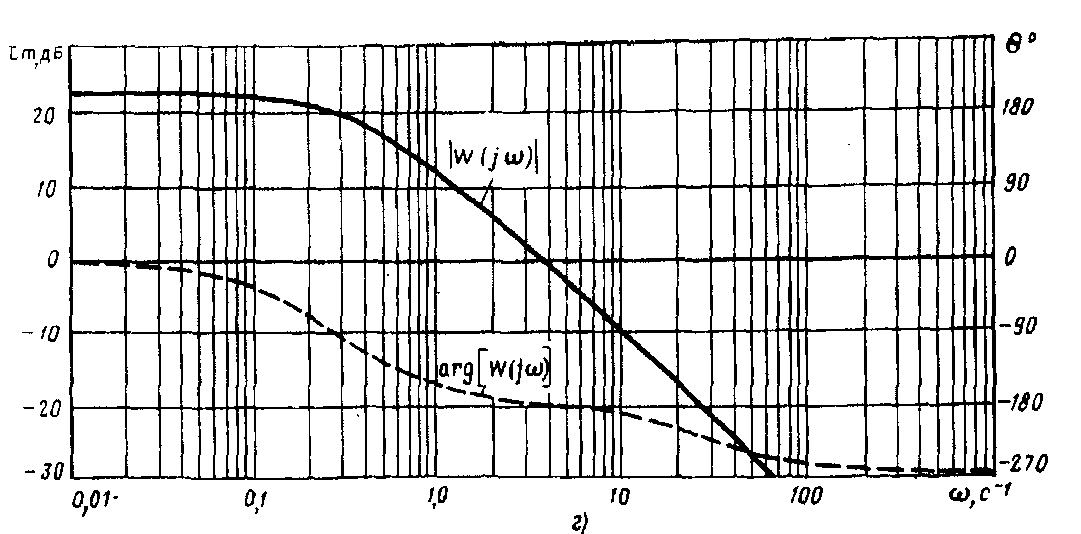
Рис. 5. Логарифмические амплитудные и фазовые частотные характеристики, при: а) ; б); в); г)

Рис. 6. Кривые D – разбиения для выделения областей

устойчивости системы в плоскости параметров

Подставим в уравнение (91) числовые значения, получим

(92)

При из уравнения (92) найдем

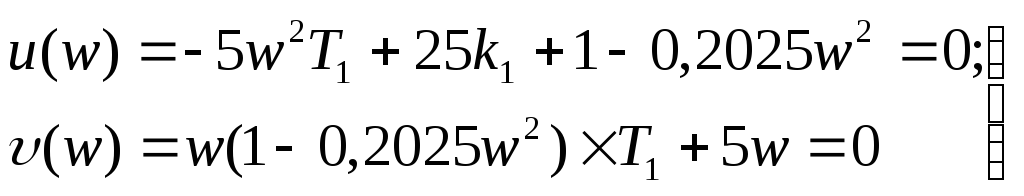(93)

Из системы уравнений (93) определим

(94)

вычислим следующие определители:

откуда

(95)

Давая w различные значения от 0 до , построим по формулам (95) кривые D-разбиения (рисунок 6). Определитель = 0 приw=0 и w= 2,222. Однако в последнем случае ине обращаются в нуль. Поэтому име­ются две особые прямые:w= 0 и w=.

Приравняв к нулю свободный член характеристического уравнения (92), получим 1 +k k₂ =0, где =-1/25 =-0,04, т. е. уравнение первой особой прямой. Приравняв = 0, найдем уравнение второй особой прямой = 0.

Воспользуемся правилом штриховки, двигаясь по кривой D-разбиения от точки w=0 к точке w= 2,222, и нанесем двойную штриховку (рисунок 6). Затем в соответствии с ранее сформулированными условиями выполним одинарную штриховку особых прямых (рисунок 6).

Для параметров = - 0,04 с иk₁ = 1 из уравнения (92) имеем один нулевой корень и к - 1 =отрицательных корней. На рис. 4.32 это показа­но точкой . Затем по правилу переходов кривыхD-разбиения и особых прямых найдем точки Т₂ - Т₆, каждой из которых соответствует свое зна­чение k+1-i (=7,2, 3). Наибольшую отметку имеют области с -к = 3. Так как порядок уравнения (92) равен трем, то зоны с =3 соответствуют областям устойчивости системы.

Кривые D-разбиения, построенные в 1-м квадрате на рисунок 6, полностью совпадают с кривыми, разделяющими области устойчивых и неустойчивых состояний (рисунок 4). Следовательно, все четыре рас­смотренные нами метода выделения областей устойчивости системы в за­висимости от изменения параметров дают одинаковые результаты.

В заключение отметим, что метод D-разбиения позволяет исследо­вать влияние как положительных, так и отрицательных параметров на об­ласти устойчивых и неустойчивых состояний, что в ряде практических за­дач представляет определенный интерес.