2. Алгебраические критерии устойчивости Гурвица, Рауса, Льенара-Шипара и Шур-Кона.

Алгебраические критерии устойчивости не требуют выполнения вычислительной процедуры определения корней характеристического уравнения при относительно невысоких порядках дифференциальных уравнений (до 15-го) позволяют находить условия асимптотической устойчивости автономных замкнутых систем.

Критерий Гурвица.

Корни характеристического уравнения 15-го порядка будут иметь отрицательные действительные части, если составленный из его коэффициентов определитель и все его диагональные миноры положительны.

Пример. Характеристическое уравнение линейной замкнутой системы имеет вид

Так как коэффициенты характеристического уравнения больше нуля, то в результате найдем Посколькутои замкнутая система асимптотически устойчива.

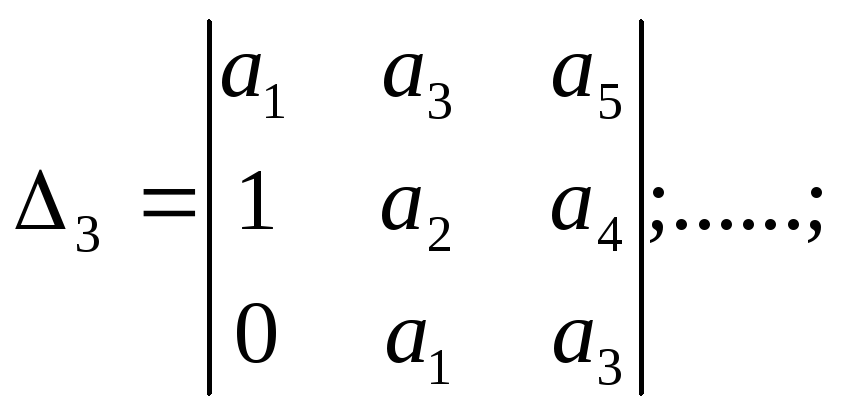
Критерий Раусса.

Зная коэффициенты характеристического уравнения, составляют таблицу Раусса. Для того чтобы замкнутая система была устойчива асимптотически, необходимо и достаточно, чтобы все коэффициенты Раусса первого столбца таблицы при были положительны, т.е.Для вычисления элементов табл. Можно использовать следующие рекуррентные формулы:

для первой строки таблицы к = 1,2,…7,…

для второй строки таблицы к = 1,2,…7,…

для остальных строк к = 1,2,…6,…i = 3,4,…13,.

Пример. Для характеристического уравнения линейной замкнутой системы, приведенного в примере выше, определены коэффициенты первого столбца:

В соответствии с критерием Рауса это указывает на асимптотическую устойчивость замкнутой системы.

Критерий Льенара – Шипара.

Запишем условия устойчивости в форме Льенара – Шипара для характеристических уравнений до 6-го порядка включительно, пользуясь определителем Гурвица. Обозначим через миноры определителя Гурвица, стоящие на главных диагоналях, где индексы:i – порядок минора, а j – степень рассматриваемого характеристического уравнения. САР будет устойчива, если при нечетные миноры главной диагонали будут положительными. Для характеристических уравнений разных степеней вида условия устойчивости имеют следующий вид:

для 1-й степени

для 2-й степени

для 3-й степени

для 4-й степени

для 5-й степени

для 6-й степени

Пример. Для характеристического уравнения линейной замкнутой системы 6-го порядка все коэффициенты характеристического уравнения больше нуля. Подставим числовые значения, получим:

что указывает на устойчивость системы.

Критерий Шур – Кона.

Данный критерий позволяет анализировать устойчивость дискретных и дискретно-непрерывных систем по характеристическому уравнению замкнутой системы, записанному в форме z – преобразования. Для уравнения n – го порядка имеем

По уравнению запишем коэффициенты в виде определителя. Корни характеристического уравнения будут находиться внутри единичной окружности, если коэффициенты уравнения удовлетворяют всем определителям.

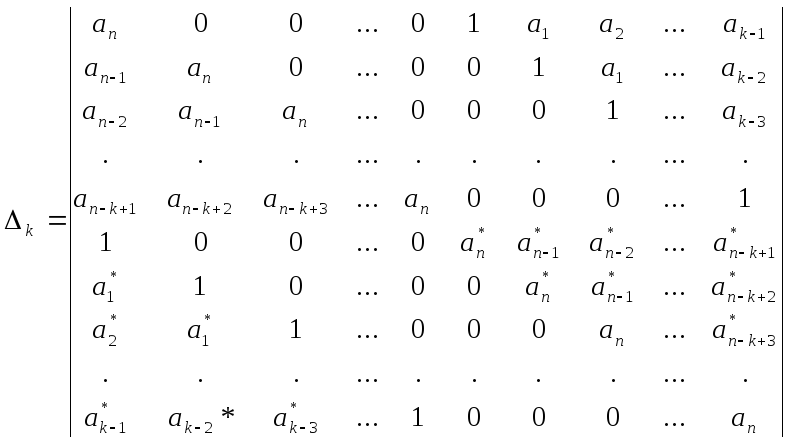
где к = 1,2,…,n, - сопряженные значения тех же коэффициентов.

Пример. Исследовать устойчивость замкнутой системы, описываемой характеристическим уравнением:

Нечетные определители: .

Четные определители: .

Из полученных определителей следует, что дискретная система ус­тойчива.