Центральный институт непрерывного образования (Общество «Знание» России) БАЛАКОВСКИЙ ИНСТИТУТ БИЗНЕСА И УПРАВЛЕНИЯ

Исследование устойчивости систем автоматического регулирования

Методические указания для студентов

специальностей:

210100 (код 65) - Управление и информатика в технических системах;

080507 (код 65) – Менеджмент организации;

080801 (код 65) – Прикладная информатика (в автомобилях и автомобильном хозяйстве).

Одобрено Редакционно-издательским советом Балаковского Института Бизнеса и Управления

Балаково 2007

ЦЕЛЬ РАБОТЫ: изучить методы исследования устойчивости ста­ционарных и нестационарных линейных непрерывных и дискретно-непрерывных САР.

Основные понятия

Понятия устойчивости стационарных и нестационарных линейных непрерывных и дискретно-непрерывных САР существенно различаются. Для случая стационарных систем необходимым и достаточным условием устойчивости следует считать такое, когда единственным положением равновесия будет начало координат, если характеристическое уравнение не имеет полюсов ни в правой части комплексной плоскости, ни на мни­мой оси при входном сигнале, равном нулю. Сразу же отметим, что для определения устойчивости систем нет необходимости вычислять корни характеристического уравнения. Необходимо только знать, как они распо­лагаются на комплексной плоскости. Для этого существуют некоторые правила, называемые критериями устойчивости.

В нестационарных системах изменение параметров может привести к нарушению сформулированного условия устойчивости стационарных систем; так, в характеристическом уравнении могут появиться полюсы как в правой полуплоскости, так и на мнимой оси. Поэтому при использовании критериев устойчивости приходится накладывать дополнительные ограни­чения.

1. Устойчивость систем по методу Ляпунова

В общем случае уравнение динамики замкнутых линейных стационарных САР будет:

Для этой системы при постоянном управляющем воздействии g (t) и наличии матрицы обратной Аз, положение равновесия находится в точке , где g(t) равно постоянной величине r. Когда управляю­щее воздействие g(t) зависит от времени, то в общем случае не представляется возможным найти такое преобразование, которое определяло бы единственное положение равновесия. Тогда исследование устойчивости линейных систем по методу Ляпунова нельзя переносить непосредственно на системы с произвольным входным воздействием. Сначала рассмотрим автономные линейные стационарные замкнутые системы.

Линейную непрерывную автономную стационарную систему мож­но описать уравнением:

(1)

Представим функцию Ляпунова в векторно-матричном виде

где

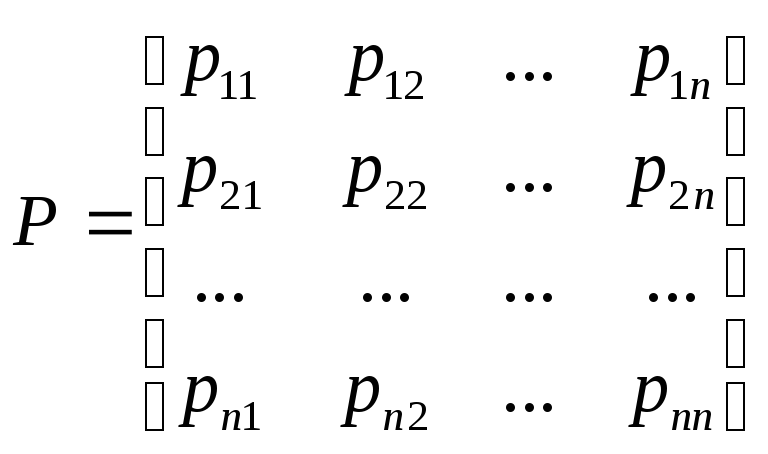(3)

или в обычной квадратичной форме

(4)

где - постоянные коэффициенты.

Квадратичная форма (3) будет положительно – определенной, если каждый из ее главных угловых миноров удовлетворяет условиям:

Пример. Допустим, что функция Ляпунова Имеет вид

тогда ее квадратичная форма

При этом миноры

Все они положительны, значит, квадратичная форма положительно определена.

Пользуясь выражением (2) можно установить, что матрица Р будет положительно-определенной при и отрицательно- определенной, когда знакоположительной, если

Существуют признаки, с помощью которых можно проверить каким из указанных выше свойств обладает матрица Р. Для этого необходимо найти собственные значения как решение характеристического уравнения

(5)

или(6)

Матрица Р положительно-определенна, если собственные значения положительны; отрицательно-определена, еслиотрицательны; знакоположительна и знакоотрицательна, еслиимеют разные знаки, и неопределенна, если

Определим производную от функции V(x), которая была записана в виде

В уравнении (7) введем следующее обозначение:

Сформулируем основное положение об асимптотической устойчивости Ляпунова.

При положительно-определенной матрице иV>0 в некоторой области , включающей в себя начало координат, положение равновесия в начале координат будет асимптотически устойчиво.

При анализе устойчивости линейных автономных систем используется также способ, связанный с исследованием корней характеристического уравнения матрицы Аз.

Обозначим корни характеристического уравнения через тогда

(8)

Раскрыв определитель (8), получим

(9)

При исследовании устойчивости в ряде случаев можно использовать уравнение

(10)

Если все корни характеристических уравнений вещественные части, то нулевое решение системы асимптотически устойчиво. Если же среди корней уравнений имеется хотя бы один корень с положительной вещественной частью, то нулевое решение системы неустойчиво. Когда уравнения не имеют корней с положительной вещественной частью, но некоторые из них содержат нулевые вещественные части, в этом случае могут возникать явления как устойчивости (не асимптотической), так и неустойчивости. Таким образом, при нулевом решении уравнения необходимо производить дополнительные исследования устойчивости.

Рассмотрим способы применения функции Ляпунова для анализа устойчивости стационарных и нестационарных систем. Дифференциальное характеристическое уравнение стационарной системы имеет вид:

(12)

где а и b – постоянные коэффициенты.

Зададимся квадратичной формой:

(13)

и представим функцию Ляпунова в виде

(14)

которая удовлетворяет уравнению

(15)

где

Подставляя значения производных из систем (12), получим Функциюзапишем в виде

(17)

Приравниваем коэффициенты при одинаковых переменных:

(18)

Имеем . Тогда систему уравнений (18) можно переписать в виде

(19)

Определитель этой системы

(20)

В качестве квадратичной формы возьмем

(21)

тогда в системе (19)

Решая систему уравнений (19), получим

В этом случае функцию Ляпунова можно записать в виде (22)

для которой имеем

(23)

Если ипроизвольная постоянная, то одновременно выполняются неравенстваив некоторой области плоскости, включающей в себя начало координат. Согласно первому методу Ляпунова система уравнений является асимптотически устойчивой в начале координат. На рис. 1, а – область устойчивого состояния системы, зависящего от параметровa и b, выделена штриховыми линиями. Существует несколько условий неустойчивости замкнутых стационарных САР. Рассмотрим условия неустойчивости системы по Ляпунову.

Первое условие неустойчивости.

Если атомная система описывается дифференциальным уравнением (1), для которой существует непрерывная функция V(x), имеющая непрерывные частные производные в области Г, включающей начало координат, такие, что , а ее производная определена вдоль всех траекторий системы, но при этом в любой окрестности начала координатне является знакоотрицательной функцией, то начало координат неустойчиво.

Второе условие неустойчивости.

Если автономной системы, описываемой дифференциальным уравнением (1), существует функция и ее производная вдоль траекторий имеет вид

(24)

где ив той же области Г, а в произвольной окрестности начала координат функцияне является знакоотрицательной, то начало координат неустойчиво.

Пример. Запишем уравнения атомной системы

Составим функцию Ляпунова в виде

(25)

откуда

(26)

Из выражений (25) и (26) следует, что автономная система неустойчива в начале координат по первому условию Ляпунова.

Рис. 1. Области асимптотической устойчивости нестационарной линейной системы в начале координат в зависимости от ее параметров, полученные с помощью применения 1-го метода Ляпунова:

а – для стационарной функции иб – для стационарной функциии условийи, условий

Пример. Запишем уравнение автономной системы

(27)

Составим функцию Ляпунова в виде

(28)

откуда

(29)

Выражение (29) перепишем в форме (24). Тогда получим

(30)

В выражении (30) и

(31)

Из выражения (29) и (30) следует, что система неустойчива в начале координат по второму условию Ляпунова. Корни характеристического уравнения (28) будут , что также характеризует неустойчивость системы.

Третье условие неустойчивости (Ляпунова – Четаева).

Допустим, что функция

а) имеет непрерывные частные производные в области , входящей в область Г с началом координат;

б) V(x) и ее производная положительно-определенны в области Г состоящей из внутренних точек области;

в) на границе V(x}=0;

г) начало координат принадлежит границе области Г.

В случае выполнения условий а)-г) начало координат неустойчиво. В отличие от стационарных систем автономные нестационарные системы описываются уравнениями вида

(32)

Для таких систем скалярная функция Ляпунова V(x, t) зависит от времени и является положительно-определенной в области Г, содержащей начало координат, если

и(33)

где — непрерывная и возрастающая функция, для которой

Наличие нестационарности систем приводит к необходимости из­менения условий устойчивости по Ляпунову.

Первое условие устойчивости. Если для системы существует поло­жительно-определенная скалярная функция V(x, t), имеющая непрерыв­ные производные по переменным х и t в некоторой окрестности. Г начала координат, а ее производная меньше нуля, то начало координаты устойчи­во.

Второе условие устойчивости. Если к первому условию добавить неравенство

(34)

то начало координат эквиасимптотически устойчиво.

Третье условие устойчивости. Если существует непрерывная строго возрастающая функция р, такая, что р(О) =0, и в дополнение к первому и второму условиям устойчивости в области Г для всех t выполняется неравенство

(35)

то начало координат системы равномерно асимптотически устойчиво.

Отметим, что при решении практических задач об устойчивости замкнутых нестационарных систем крайне желательно выбирать функцию V, не зависящую от времени t. Тогда для равномерной асимптотической устойчивости необходимо иметь V(x)>0, хО,V(0)=0, и функция произ­водной должна удовлетворять условию (33). При этом существенно упро­щается анализ устойчивости нестационарных систем.

Дифференциальное характеристическое уравнение нестационар­ной системы запишем в виде

(36)

или

(37)

Исследование замкнутой системы (36) состоит в том, чтобы на функции a(t) и b(t) были наложены такие ограничения, при которых обес­печивается асимптотическая устойчивость в начале координат. Для этого необходимо найти функцию Ляпунова. Известно, что можно сформиро­вать две функции Ляпунова, если положить

(38)

или нестационарную, когда

(39)

при

Для стационарной функции Ляпунова при ифункция положительно-определенна, и для нее справедливо соотношение

откуда

(41)

Если и коэффициент приположителен, то производная будет отрицательно-определенной. В этом случае получим

(42)

После ряда преобразований неравенство (42) перепишем в виде

(43)

Из выражения (43) следует, что

(44)

Если неравенства (43) и (44) записать в виде равенств и воспользоваться условием , то на плоскости (a,b) можно найти область, где обеспечивается асимптотическая устойчивость. Эта область на рис. 1, а выделена штрихами. Кривая 1 соответствует уравнению параболы

(45)

прямая 2–условию:

(46)

а кривая 3 – уравнению:

(47)

Учитывая условия: , гдепостоянные параметры, постоим на рис.1,6 штриховой линией параболу 2.

(48)

При этом видно, что она проходит через точку с координатами

При этом нижняя ветвь параболы 2 проходит через очку с координа­тами когда . Подставляя эти координаты в уравнения, найдем два уравнения относительно . Исключив р₂, определим . Затем, записав через, получим

(49)

Так как является действительным числом, то, нетрудно показать, что

(50)

Из уравнений (47), (48) определим ординаты парабол при постоянном значении. Для этого воспользуемся уравнениями

(51)

Полученная с помощью парабола 1 изображена на рисунке сплошной линией. Выражение (50) можно переписать в виде

(52)

Найдем

(53) (54)

Откуда получим необходимые условия для определения коэффициентов

(55)

В соответствии с неравенствами на рис. 1,6 штрихами выделена внутренняя область, определяемая этими параболами, в которой возможна асимптотическая устойчивость системы в начале координат.

Для нестационарной функции Ляпунова найдем

(56)

Принимая

(57)

имеем

(58)

Функция знакоотрицательна и начало координат асимптотически устойчиво, так какV(x,t)>0 и имеет непрерывные производные по x и t в окрестности начало координат, а V(x,t)<0.

Рассмотрим применение первого метода Ляпунова к дискретным или дискретно-непрерывным системам, приведенным к дискретным моделям. В этом случае автономное уравнение замкнутой системы можно записать в виде

(59)

Функция Ляпунова имеет вид

(60)

Обозначим первую разность этой функции на траекторииследующим образом:

(61)

или

(62)

где Q – симметричная положительно-определенная матрица вида:

(63)

Автономная дискретная система (59) будет устойчива, если существуют положительно-определенные симметричные матрицы. Р и Q, которые удовлетворяют соотношению:

(64)

Из выражения (60) следует, что

(65)

(66)

Если рассматриваемая система (65) асимптотически устойчива, то из уравнения (66) получим искомую функцию Ляпунова:

.

функция положительно-определенна, и ряд сходится.

Пример. Необходимо исследовать устойчивость дискретной линейной системы по Ляпунову, описываемой уравнением ви

Выбирая Q=1 имеем

Так как , получим систему уравнений

откуда найдем матрицу

Ее диагональные миноры и, поэтому матрица Р положительно-определенна, а автономная замкнутая система, согласно выполнению условия устойчива.